آموزش ریاضی پایه دهم
مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
در فصل اول ریاضی دهم و بخش اول آن با مفهوم مجموعه در ریاضی آشنا میشویم. این بخش شامل موارد زیر است که در این نوشتار به آموزش کامل تمامی آنها خواهیم پرداخت:
- مفهوم مجموعهها
- زیر مجموعه
- تساوی دو مجموعه
- نمایش زیر مجموعه های اعداد حقیقی به صورت بازه
- مجموعه متناهی و نامتناهی
مفهوم مجموعه در ریاضی
همانطور که در سالیان قبل یاد گرفتید مجموعه جزء مفاهیم تعریف نشده میباشد. اما مفهوم مجموعه در ریاضی عبارت است از
دستهای از اشیاء یا اعداد که دارای خاصیت مشترک میباشند.
وقتی از مجموعه صحبت میکنیم باید اعضای مجموعه مشخص باشد. مثلاً وقتی میگوییم جمعیت کشور ایران، دقیقاً مشخص است که در مورد چه کسانی صحبت میکنیم. ولی وقتی گفته میشود نام 3 گل زیبا، نام سه تن از شعرای معروف، و یا جمعیت افراد خوشتیب در ایران، اعضای این مجموعهها مشخص نیستند. چون خوشتیپ بودن یا معروف بودن عوامل نسبی هستند.
چند مثال برای فهم بهتر
اجازه بدهید بیشتر باهم بررسی کنیم. معیار زیبایی یک معیار کاملاً مشخص نیست. این مثال زیر را در نظر بگیرید: 3 عدد طبیعی زوج متوالی. اعضای این مجموعه مشخص نیستند. ولی وقتی میگوییم اعداد زوج طبیعی کوچکتر از 10، کاملاً اعضای این مجموعه مشخص است.
در مجموعه تکرار یا ترتیب مهم نیست. مثلاً اگر در لیست اسامی دانش آموزان کلاس ۳۱ نفری نام شخصی دوبار نوشته شده باشد، آن کلاس بازهم 31 نفر عضو دارد. همچنین نوشتن نام اعضای این کلاس با هر ترتیبی مهم نیست. پس وقتی در مورد یک مجموعه صحبت میکنیم دو نکته زیر را حتماً باید در نظر گرفت:
- باید اعضای مجموعه کاملاً مشخص و معلوم باشند.
- تکرار و ترتیب در آنها مهم نیست.
البته لازم به ذکر است که معمولاً سعی میکنیم اعضای مجموعه را با ترتیب خاص بنویسیم. اما اگر ترتیب به هم بخورد مجموعهٔ جدیدی پدید نمیآید.
زیر مجموعه
یکی دیگر از نکاتی که در بحث مفهوم مجموعه در زیاضی می آموزیم بحث زیر مجموعه است. مجموعه \( \Large A \) و \( \Large B \) را در نظر بگیرید. اگر هر عضوی که در \( \Large A \) هست در \( \Large B \) هم موجود باشد، یا به عبارتی \( \Large A \) جزئی از \( \Large B \) باشد، میگوییم مجموعه \( \Large A \) زیر مجموعهٔ \( \Large B \) است و مینویسیم:

تساوی دو مجموعه
یکبار دیگر دو مجموعهٔ \( \Large A \) و \( \Large B \) را در نظر بگیرید. اگر:

و

باشند، این بدان معنی است که:
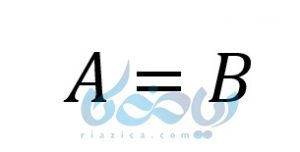
مثال ۱:

مجموعههای مهم در ریاضی
- مجموعه اعداد طبیعی
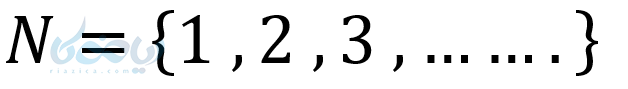
- مجموعه اعداد حسابی
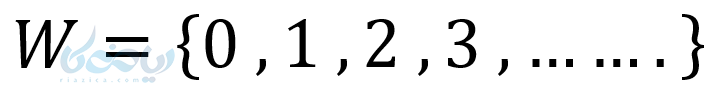
- مجموعه اعداد صحیح
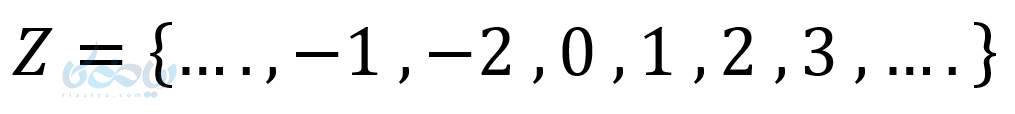
- مجموعه اعداد گویا
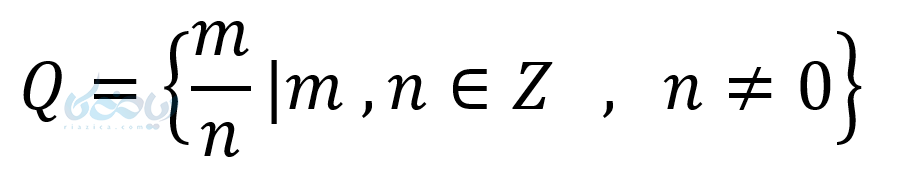
- مجموعه اعداد گنگ: مجموعه اعدادی که نتوان آن ها را به صورت نسبت دو عدد صحیح نمایش داد.
- مجموعه اعداد حقیقی
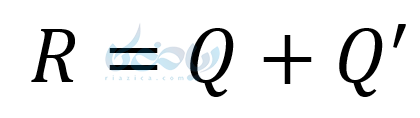
در حقیقت مفهوم مجموعه در ریاضی میگوید که تمام مجموعهٔ اعدادی که تاکنون خواندهایم، زیر مجموعه اعداد حقیقی هستند.

بازه ها
برای نمایش زیر مجموعه های اعداد حقیقی در سالهای قبل 3 روش آموخته بودید.
- روش توصیفی
مثال مجموعه اعداد حقیقی بزرگتر از 3
- زبان ریاضی یا نمایش مجموعه

- روش هندسی
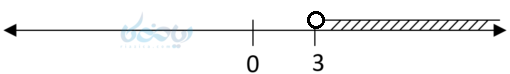
اما برای راحتر توشتن زیر مجموعه های اعداد حقیقی روش دیگری هست به نام نمایش بازه ای. بازه ها 3 نوع هستند:
- باز
- بسته
- نیمه باز
که به صورت های زیر نمایش داده میشوند:
- بازه باز
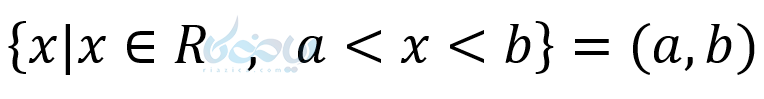
- بازه نیمباز
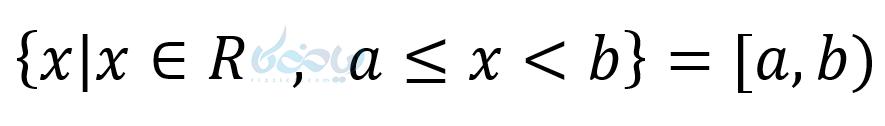
- بازه نیمباز
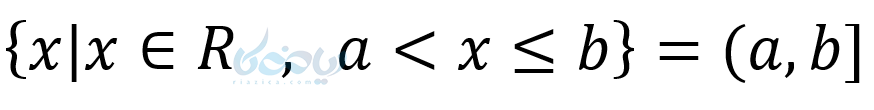
- بازه بسته
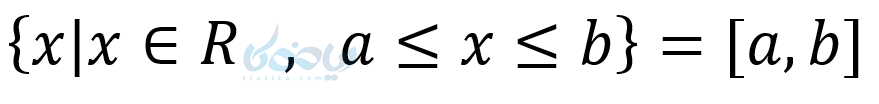
نکته ۱: اگر زیر مجموعه اعداد حقیقی بزرگتر از یک عدد باشد، به سمت مثبت بینهایت میروند. در ریاضیات نماد زیر نماد مثبت بی نهایت است.
\( \Large +\infty \)
همچنین نماد زیر در ریاضیات نماد منفی بی نهایت است.
\( \Large -\infty \)
طبق نکته ۱ میتوانیم بنویسیم:
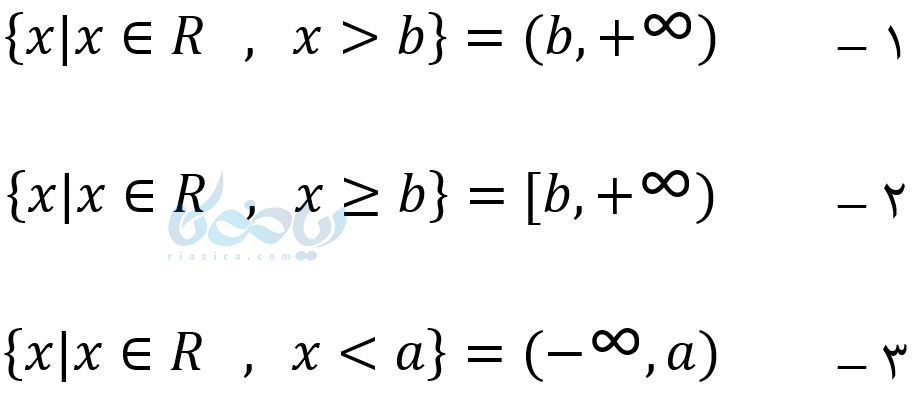
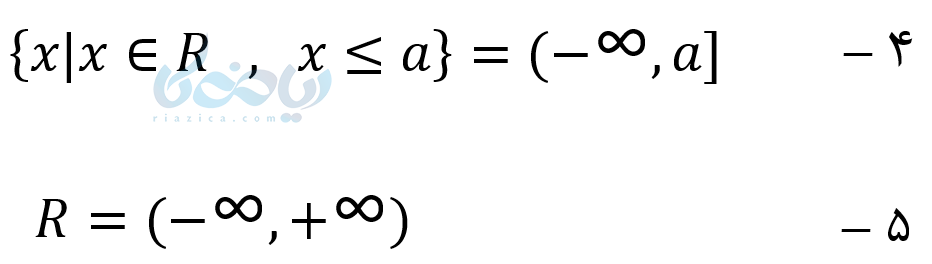
نکته ۲: همیشه در بازه ها سمت چپ عدد کوچکتر و سمت راست عدد بزرگتر نوشته میشود.
نکته ۳: همیشه کنار نماد \( \Large +\infty \) و \( \Large -\infty \) از پرانتز که نماد باز بودن است استفاده میشود.
توجه : توجه داشته باشید که فقط زیر مجموعه های اعداد حقیقی را میتوان به صورت بازه نوشت و زیرمجموعه بقیه مجموعه ها را به روش قبلی فقط میتوان نمایش داد.
اَعمال روی بازه ها
شما در سالهای قبل با اشتراک، اجتماع و تفاضل مجموعه ها آشنا شدید. این اَعمال را روی بازه ها نیز میتوان اعمال کرد.
چند مثال ۲:
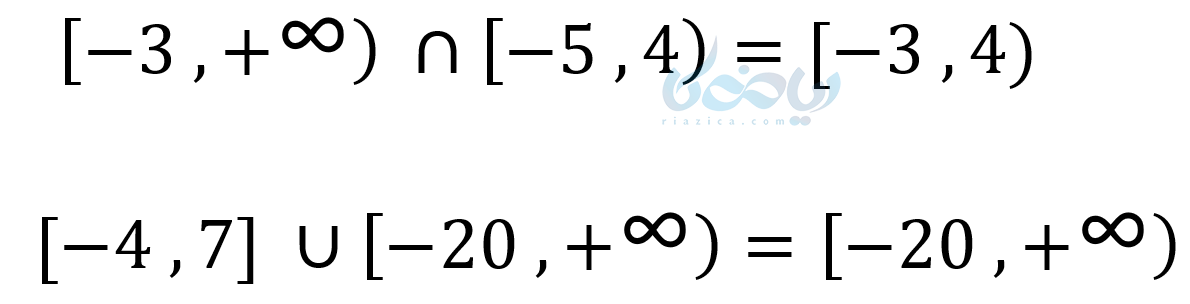
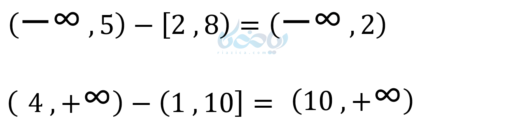
دقت کنید اگر نمیتوانید این اعمال را به صورت ذهنی انجام دهید، میتوانید با استفاده از محور به آسانی این کار انجام دهید. مثلاً:
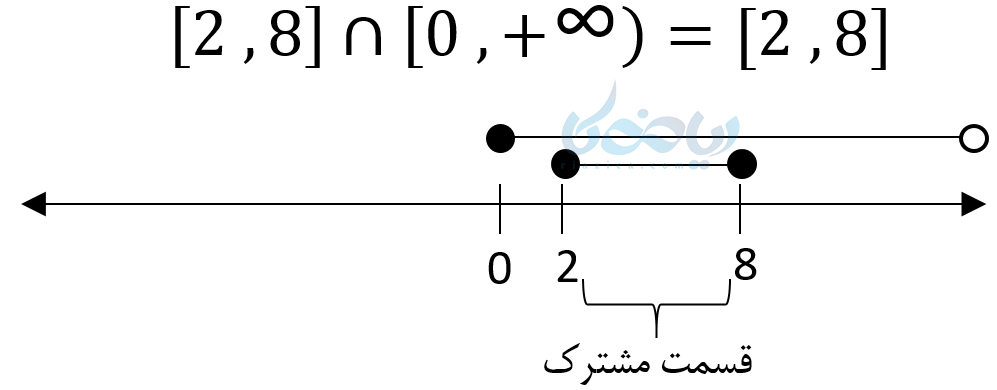
مجموعه متناهی و نامتناهی
در بحث مفهوم مجموعه در ریاضی پیمیبریم که مجموعه متناهی مجموعه ای است که تعداد اعضای آن یک عدد حسابی باشد.
مثال ۳: مجموعه اعداد اول یک رقمی یک مجموعه متناهی است.

سوال مهم: ممکن است تعداد اعضای یک مجموعه متناهی بسیار زیاد باشند و به نظر برسد که نتوان آنها را شمرد. آیا باز این مجموعه را می توان یک مجموعه متناهی محسوب کرد؟
جواب: پاسخ به این سوال مثبت است. چون با داشتن امکانات و صرف وقت کافی ممکن است بتوان تعداد آنها را به دست آورد. یا به عبارت دیگر تعداد آنها به شرطی که توانایی شمردنشان را داشته باشیم، بالاخره به پایان میرسد.
مثل تعداد مورچگان کره زمین. تعداد آنها خیلی زیاد است اما قابل شمارش هستند. و یا تعداد درختهای جنگلهای آمازون. و یا تعداد اتمهای یک جسم. همه مثالهایی از این نوع هستند.
مجموعهای که نتوان تعداد اعضای آن را با یک عدد حسابی بیان کرد، مجموعه نامتناهی است.
مثال ۴: \( \Large A=(0,1) \) . تعداد اعضای این بازه قابل شمارش نیستند. چون بین هر دو عدد حقیقی بی نهایت عدد حقیقی دیگر وجود دارد.
مثال ۵: اعداد گویا بین 3 تا 2- را در نظر بگیرید. دوباره این مجموعه یک مجموعه نامتناهی است. چون بین هر دو عدد گویا بی نهایت عدد گویا دیگر می توان نوشت.
در مورد مفهوم مجموعه در ریاضی بیشتر بدانیم
مثال ۶: بین دو عدد \( \LARGE \frac{1}{2}\) و \( \LARGE \frac{1}{3}\) سه عدد گویا بنویسید.
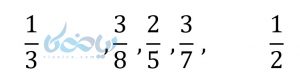
برای اینکار کافی است صورت و مخرج کسرها را با هم جمع کنیم. کسر \( \LARGE \frac{2}{5} \) از \( \LARGE \frac{1}{3}\) بزرگتر و از \( \LARGE \frac{1}{2}\) کوچکتر است.
بین \( \LARGE \frac{1}{3}\) و \( \LARGE \frac{2}{5}\) نیز میتوان کسرهای دیگری را مانند \( \LARGE \frac{3}{8}\) نوشت.در نتیجه میتوان نتیجه گرفت که بین این دو کسر، بی نهایت عدد گویا دیگر نیز وجود دارند.
پاسخ به سوالات شما
اگر هر سوالی در رابطه با مفهوم مجموعه ها در ریاضی دارید، میتوانید در زیر همین پست در بخش نظرات از ما بپرسید. گروه آموزشی ریاضیکا در سریعترین زمان ممکن به شما پاسخ میدهند.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!





سلام
نمونه سوال واسه این آموزش دارید؟
ضمن عرض سلام و احترام
این دو تا لینک محصولاتی هست که به این آموزش مربوط هستند
https://riazica.com/product/set-complement-quiz-1/
https://riazica.com/product/finite-and-infinite-set-quiz-1/
سلام وقت بخیر
ببخشید اعمال روی بازه ها و مورد آخر مثال جوابش (بینهایت +و ۱۰ ) فقط نمیشه ؟
با سلام
یله دوست عزیز اصلاح شد
اشتراکها: مجموعه ها ریاضی تیزهوشان نهم 💎💡 - نمونه سوال هایی که دنبالش بودی!! - ریاضیکا | ریاضی آسان است
سلام و درود
استادبزرگوار اگر اشتراک دو بازه تهی باشد چگونه نمایش دهیم
با سلام دوست عزیز
از علامت مجموعه تهی یا دو آکولاد خالی
تصویر اول (فرمول زیرمجموعه) در مورد زیرمجموعه، باید B زیرمجموعه A باشه که فرمول برعکس نوشته شده.
با سلام
ممنون از دقت نظر شما اصلاح شد