آموزش ریاضی پایه دهم
آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
آیا تاکنون به حرکت توپ در زمین فوتبال دقت کردهاید؟ حرکت آن یک حرکت سهمیوار است که ابتدا اوج میگیرد. سپس در یک لحظه سرعتش به صفر میرسد و به سمت زمین برمیگردد. ما در این بخش میخواهیم به معادله درجه دو و حل آن بپردازیم که در واقع نمودار آن یک سهمی است.
در خیلی از مسائل ریاضی، هندسه، شیمی، فیزیک به معادله درجه دو و حل آن برمیخوریم که لزوم شناخت معادله درجه دو و یادگیری حل آن را نشان میدهد.
تشخیص معادله درجه دو
در ریاضیات پایه دهم یاد میگیریم، هر معادلهای که بعد از ساده شدن تمام متغیرهایش، بزرگترین توان متغیرهای آن عدد ۲ باشد، معادله درجه دوم نامیده میشود.
به مثالهای زیر دقت کنید:
(1
\( \LARGE x^2 = 4 \rightarrow x^2-4=0 \)
(2
\( \LARGE x(x+1)=5 \)
\( \LARGE \rightarrow x^2+x-5=0 \)
(3
\( \LARGE x^2-3x=4 \)
\( \LARGE \rightarrow x^2-3x-4=0 \)
(4
\( \LARGE x^2 +(x+1)^2=(x+2)^2 \)
\( \LARGE \rightarrow x^2-2x-3=0 \)
(5
\( \LARGE -2x^2 -x=0 \)
تمام مثالهای بالا یک معادله درجه دوم را نشان میدهند. حال به مثال زیر دقت کنید:
\( \LARGE x(x+1)=(x-2)^2 \)
\( \LARGE x^2 + x=x^2-2x+4 \)
\( \LARGE -x-4=0 \)
این معادله بعد از ساده شدن به یک معادله درجه اول تبدیل شد. پس اگر معادلهای را ساده کردیم و به فرم \( \Large ax^2 + bx + c =0 \) درآمد، چنین معادلهای یک معادله درجه دوم است.
تعریف معادله درجه دوم
هر معادله به شکل \( \Large ax^2 + bx + c =0 , a \neq 0 \) که در آن \( \Large a , b , c \) اعداد حقیقی باشند، را یک معادله درجه دوم مینامیم.
برای حل معادله درجه دوم روشهای گوناگونی وجود دارد که در کتاب ریاضی دهم به چهار مورد از آنها اشاره شده است. قبل از بیان این روشها به نکته زیر دقت کنید.
ویژگی مهم حاصلضرب صفر
اگر \( \Large A , B \) دو عبارت جبری باشند که حاصلضرب آنها صفر باشد، یعنی: \( \Large AB = 0 \) آنگاه حداقل یکی از این دو عبارت صفر است. یعنی:
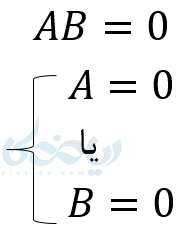
ما از این ویژگی در حل معادله درجه دو به روش تجزیه استفاده میبریم.
روشهای حل معادله درجه دو
- تجزیه
- ریشهگیری
- روش مربع کامل
- روش کلی یا دلتا \( \LARGE \Delta \)
1- تجزیه
هرگاه بخواهیم یک معادله درجه دو که تجزیهپذیر است را از روش تجزیه حل کنیم به این شکل عمل میکنیم:
- در ابتدا آن را ساده کرده و تمام جملات را به یک طرف برده و طرف دوم را صفر قرار میدهیم.
- حال از روشهای گفته شده در درس تجزیه ،معادله را در صورت تجزیه شدن ،تجزیه میکنیم.
- در نهایت از ویژگی حاصلضرب صفر برای پیدا کردن جوابها کمک میگیریم.
به حل معادله زیر دقت کنید:
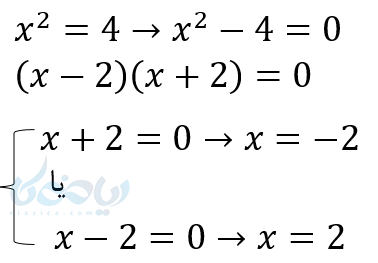
تجزیه به روش مزدوج
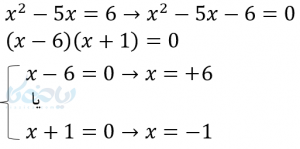
تجزیه به روش اتحاد جمله مشترک
در دو مثال بالا هر دو معادله، دو جواب داشتند. باید دقت کنیم معادله درجه دو میتواند حداکثر دو جواب یا یک جواب یا اصلاً جواب نداشته باشد.
نکته ۱: به جواب معادلات، ریشه معادله هم گفته میشود. منظور ما از ریشه عددی است که عبارت به ازای آن صفر میشود.
به مثال زیر دقت کنید:
\( \LARGE x^2 =4(x-۱) \)
\( \LARGE \rightarrow x^2-4x+4=0 \)
\( \LARGE \rightarrow (x-2)^2=0 \)
\( \LARGE \rightarrow x-2=0 \)
\( \LARGE \rightarrow x=2 \)
معادله فقط یک جواب دارد.
\( \LARGE x^2 -5x=0 \)
\( \LARGE \rightarrow x(x-5)=0 \)
\( \LARGE \rightarrow \begin{cases} x=0 \\ x-5=0 \end{cases} \)
\( \LARGE \rightarrow x=5 \)
نکته ۲: دقت کنید هرگاه در معادله درجه دو \( \Large c=0 \) باشد، حتماً یکی از جوابها صفر خواهد بود. در این موارد بهتر است همیشه از روش فاکتورگیری عمل تجزیه را انجام دهیم.(مانند مثال بالا)
نکته ۳: دقت کنید روش تجزیه یک روش کلی نیست و فقط مواقعی که معادله تجزیهپذیر است استفاده میشود.
2- روش ریشهگیری
این روش هم مثل روش تجزیه یک روش کلی نیست و در یکی از شرایط زیر استفاده میشود:
- \( \Large b=0 \) باشد
- یک طرف اتحاد مربع دوجملهای و در طرف دیگر عدد مثبت داشته باشیم.
به این مثال دقت کنید: \( \LARGE x^2 – 4 =0 \) ما این معادله را در بالا به روش تجزیه حل کردیم اما برای این معادله روش ریشهگیری خیلی بهتر و سریعتر است. کافیست \( \Large x^2 \) بدون ضریب به یک طرف و \( \Large c \) به طرف دیگر برده شود. اگر طرف دوم مثبت باشد از دو طرف ریشه دوم میگیریم و معادله دو جواب دارد. همچنین اگر منفی باشد معادله جواب نخواهد داشت.
در این مثال داریم:
\( \LARGE x^2 – 4 =0 \)
\( \LARGE \rightarrow x^2=4 \)
\( \LARGE \rightarrow x=\pm 2 \)
دو جواب دارد.
\( \LARGE x^2 =0 \)
\( \LARGE \rightarrow x=0 \)
یک جواب دارد.
\( \LARGE 2x^2 = 12 \)
\( \LARGE \rightarrow x^2=6 \)
\( \LARGE \rightarrow x=\pm \sqrt6 \)
دو جواب دارد.
\( \LARGE 2x^2 + 14 =0 \)
\( \LARGE \rightarrow x^2=-7 \)
معادله جواب ندارد یا ریشه ندارد. یعنی هیچ عدد حقیقی یافت نمیشود که در این معادله صدق کند. پس به طور کلی میتوان گفت:
اگر \( \Large c \) یک عدد حقیقی نامنفی (بزرگتر یا مساوی صفر) باشد با ریشههای معادله درجه دوم \( \Large x^2 = c \) عبارتند از: \( \Large x= \sqrt c , x= -\sqrt c \)
به مثال دیگری دقت کنید:
\( \LARGE (x-2)^2=25 \)
در این مثال هم چون طرف اول مجذرو کامل است میتوان با ریشهگیری از دو طرف و بدون توان رساندن و سادهکردن جواب را بدست آورید.
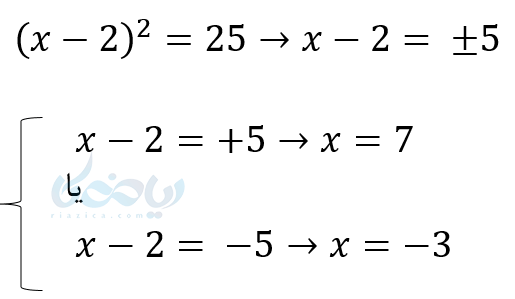
البته ما در سوالات کمتر به این نمونهها بر میخوریم. ولی در روش مربع کامل از این روش زیاد استفاده میشود.
3- روش مربع کامل
روش مربع کامل را در حقیقت برای اولین بار توسط خوارزمی به کار برده شد. اما نه به این شیوه کامل کنونی. بعدها ریاضیدانان با کامل کردن روش خوارزمی به این روش رسیدند. روشی که از روی آن روش کلی و \( \Large \Delta \) را بدست میآوریم.
ما در سالهای آینده از خود این روش استفاده نمیکنیم. بلکه این روش را به صورت فرمولی درآورده (روش \( \Large \Delta \)) و از آن استفاده میکنیم خود این روش یک روش کلی محسوب میشود و برای حل همه معادلات میتوان از آن استفاده کرد.
مثال ۱: معادله \( \Large x^2-5x+6=0 \) را به روش مربع کامل حل کنید.
حل ۱:
- ابتدا \( \Large c \) را به طرف دوم برده یا بهتر بگوییم قرینه \( \Large c \) را به دو طرف اضافه میکنیم.
\( \LARGE x^2-5x=-6 \)
- طرف اول را به صورت مربع کامل در میآوریم. برای اینکار \( \Large b \) یعنی ضریب \( \Large x \) را نصف و به توان دو رسانده و عدد بدست آمده را به دو طرف اضافه میکنیم. (\( \LARGE \frac{b^2}{4} \))
\( \LARGE x^2-5x+\frac{25}{4} \)
\( \LARGE =-6+\frac{25}{4} \)
- طرف اول که اکنون مربع کامل است را تجزیه میکنیم و حاصل طرف دوم را بدست میآوریم.
\( \LARGE (x-\frac{5}{2})^2=\frac{1}{4} \)
- اگر طرف دوم منفی شد که معادله جواب ندارد. اما اگر مثبت شد دو جواب و اگر صفر شد یک جواب دارد. حال به روش ریشهگیری از دو طرف ریشه میگیریم. در نهایت جوابها را بدست میآوریم.
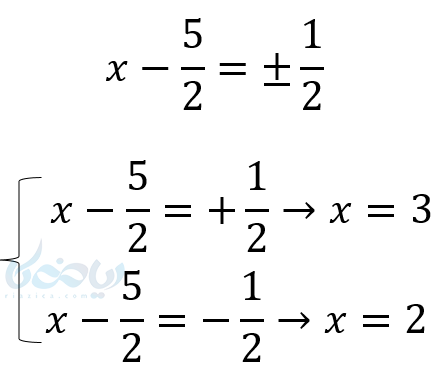
به نمونه دیگری دقت کنید. \( \LARGE x^2-8x+4=0 \)
- \( \LARGE x^2-8x=-4 \)
- \( \LARGE x^2-8x+16=-4+16 \)
- \( \LARGE (x-4)^2=12 \)
- \( \LARGE x-4= \pm \sqrt 12 \)
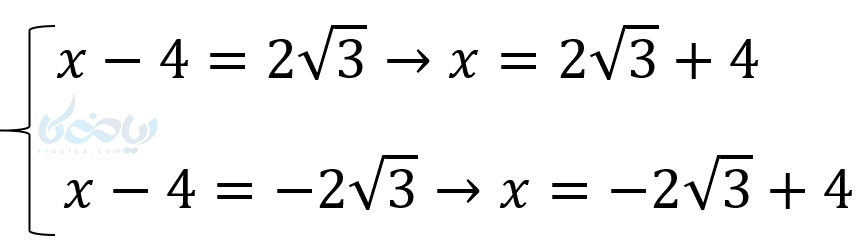
نکته ۴: اگر \( \Large x^2 \) ضریب داشت، یعنی \( \Large a>1 \) بود، ابتدا تمام جملات را به ضریب \( \Large a \) تقسیم میکنیم. سپس از روش مربع کامل استفاده میکنیم.
\( \LARGE 2x^2-3x+4=0 \)
به 2 تقسیم میکنیم.
\( \LARGE x^2-\frac{3}{2}x+2=0 \)
\( \LARGE \rightarrow x^2-\frac{3}{2}x=-2 \)
\( \LARGE \rightarrow x^2-\frac{3}{2}x + \frac{9}{16} \)
\( \LARGE =-2+\frac{9}{16} \)
\( \LARGE \rightarrow (x-\frac{3}{4})^2=-\frac{23}{16} \)
معادله جواب نداردچون طرف دوم منفی شده.
4-حل معادله درجه دوم به روش فرمول کلی یا دلتا \( \LARGE \Delta \)
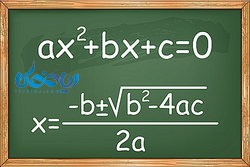
در واقع همانطور که قبلا گفته شد، روش فرمول کلی همان روش مربع کامل است. که به صورت فرمولی نوشته شده و میتوان با داشتن دو فرمول، سریعتر به جوابها رسید.
گفتیم فرم کلی معادلات درجه دوم به صورت \( \Large ax^2 + bx + c =0 , a \neq 0 \) است. حال با یکدیگر این فرم را به روش مربع کامل حل میکنیم.
- چون \( \Large x^2 \) ضریب \( \Large a \) را دارد، ابتدا معادله را به \( \Large a \) تقسیم میکنیم.
\( \LARGE ax^2 + bx+c=0 \)
\( \LARGE \rightarrow x^2 + \frac{b}{a}x + \frac{c}{a} = 0 \)
- قرینه \( \LARGE \frac{c}{a} \) را به دو طرف اضافه میکنیم (یا به زبان ساده \( \LARGE \frac{c}{a} \) را به طرف دوم میبریم).
\( \LARGE x^2+\frac{b}{a}x = -\frac{c}{a} \)
- ضریب \( \Large x \) یعنی \( \LARGE \frac{b}{a} \) را نصف کرده که میشود \( \LARGE \frac{b}{2a} \) و سپس به توان 2 میرسانیم که میشود \( \LARGE \frac{b^2}{4a^2} \) . در ادامه آن را به دو طرف معادله اضافه میکنیم.
\( \LARGE x^2 + \frac{b}{a}x + \frac{b^2}{4a^2} \)
\( \LARGE =- \frac{c}{a} +\frac{b^2}{4a^2} \)
- طرف اول را تجزیه و طرف دوم را محاسبه میکنیم.
\( \LARGE (x+\frac{b}{2a})^2 = \frac{b^2-4ac}{4a^2} \)
- حال در طرف دوم، مخرج که مجذور کامل و مثبت است. پس علامت کسر به صورت، یعنی \( \Large b^2-4ac \) بستگی دارد. اگر این عبارت مثبت باشد، معادله دو جواب دارد. اگر صفر باشد یک جواب و اگر منفی باشد جواب ندارد. برای همین به \( \Large b^2-4ac \)
مبیّن یا روشن کننده میگویند و اسم آن را (دلتا )\( \Large \Delta \) که یک حروف یونانی است قرار میدهند. یعنی:
\( \LARGE \Delta = b^2-4ac \)
خوب اگر \( \Large \Delta >0 \) باشد باید از دو طرف ریشه دوم بگیریم و داریم:
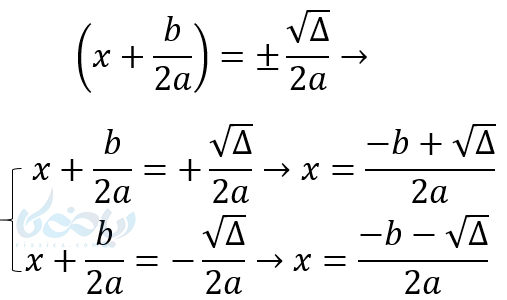
پس اگر \( \Large \Delta>0 \) باشد دو جواب داریم که از رابطه \( \LARGE x=\frac{-b\pm \sqrt{\Delta}}{2a} \) به دست میآید.
به طور خلاصه داریم:

به چند مثال برای بهتر فهمیدن این مطلب دقت کنید. (نکته: در این روش باید همه جملات یک طرف و طرف دوم صفر باشد.)
مثال ۲: معادلات زیر را به روش فرمول کلی یا دلتا \( \Large \Delta \) حل کنید.
حل ۲:
(1
\( \LARGE x^2+7x=-12 \)
\( \LARGE x^2+7x+12=0 \)
\( \LARGE a=1,b=7,c=12 \)
\( \LARGE \Delta = b^2-4ac \)
\( \LARGE = 49-4\times 1 \times 12 \)
\( \LARGE = 49-48=1 \)
چون \( \Large \Delta >0 \) پس دو جواب دارد.
\( \LARGE x=\frac{-b\pm \sqrt{\Delta}}{2a} = \frac{-7\pm \sqrt{1}}{2} \)
\( \LARGE x_1 =-3 , x_2=-4 \)
(2
\( \LARGE -2x^2+x+3=0 \)
\( \LARGE a=-2,b=1,c=3 \)
\( \LARGE \Delta = b^2-4ac \)
\( \LARGE = 1-4\times (-2) \times 3 \)
\( \LARGE = 1+24=25 \)
چون \( \Large \Delta >0 \) پس دو جواب دارد.
\( \LARGE x=\frac{-b\pm \sqrt{\Delta}}{2a} = \frac{-1\pm \sqrt{25}}{-4} \)
\( \LARGE x_1 =-1 , x_2=+\frac{3}{2} \)
(3
\( \LARGE x(x-1)=-1 \)
\( \LARGE x^2-x+1=0 \)
\( \LARGE a=1,b=-1,c=1 \)
\( \LARGE \Delta = b^2-4ac \)
\( \LARGE = 1-4\times 1 \times 1 \)
\( \LARGE = 1-4=-3 \)
چون \( \Large \Delta <0 \) پس جواب ندارد.
(4
\( \LARGE x^2-6x+9=0 \)
\( \LARGE a=1,b=-6,c=9 \)
\( \LARGE \Delta = b^2-4ac \)
\( \LARGE = 36-4\times 9 \times 1 \)
\( \LARGE = 36-36=0 \)
چون \( \Large \Delta =0 \) پس یک جواب دارد.
\( \LARGE x=\frac{-b}{2a} = \frac{6}{2} = 3 \)
(5
\( \LARGE x^2-6x+4=0 \)
\( \LARGE a=1,b=-6,c=4 \)
\( \LARGE \Delta = b^2-4ac \)
\( \LARGE = 36-4\times 4 \times 1 \)
\( \LARGE = 36-16=20 \)
چون \( \Large \Delta >0 \) پس دو جواب دارد.
\( \LARGE x=\frac{-b\pm \sqrt{\Delta}}{2a} \)
\( \LARGE x=\frac{6\pm \sqrt{20}}{2} \)
\( \LARGE x=\frac{6\pm 2\sqrt 5}{2} \)
\( \LARGE x=\frac{2(3\pm \sqrt 5)}{2} \)
\( \LARGE x_1=3+\sqrt 5 \)
\( \LARGE x_2=3-\sqrt 5\)
مثال ۳: معادله \( \Large a^2 + 2\sqrt 3 a = 9 \) را به روش کلی حل کنید. (تمرین ۴ صفحه ۷۷ کتاب ریاضی دهم)
حل ۳:
چند نکته در مورد حل معادله درجه دو
- اگر در معادله درجه دوم \( \Large b=0 \) باشد بهترین روش، روش ریشهگیری بوده و در صورت وجود جواب، جوابها قرینه یکدیگرند.
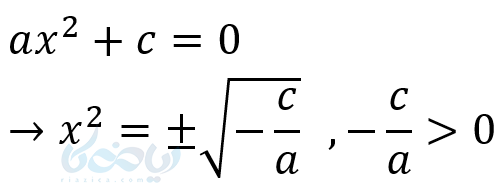
- اگر \( \Large c=0 \) باشد بهترین روش، روش تجزیه به روش فاکتورگیری است که حتما یک جواب صفر است.
\( \LARGE ax^2+bx=0 \)
\( \LARGE x(ax+b)=0 \)
\( \LARGE \rightarrow x_1=0 , x_2= -\frac{b}{a} \)
- اگر \( \Large a+b+c=0 \) باشد حتما یکی از جوابها یک خواهد بود.
\( \LARGE x^2+2x-3=0 \)
\( \LARGE 1+2-3=0 \)
\( \LARGE (x-1)(x+3)=0 \)
\( \LARGE x_1=1 , x_2=-3 \)
- اگر \( \Large a+c=b \) باشد حتما یکی از جوابها 1- خواهد بود.
\( \LARGE x^2+3x+2=0 \)
\( \LARGE 1+2=-3 \)
\( \LARGE (x+1)(x+2)=0 \)
\( \LARGE x_1=-1 , x_2=-2 \)
- اگر \( \Large c , a \) مختلف العلامت باشند، یعنی علامتشان با هم فرق داشته باشد حتما معادله دو جواب دارد.
آخر کلاس آموزش حل معادله درجه دو
در بخش رسم نمودار یاد میگیریم که میتوان جوابهای معادله درجه دو را از روی نمودار آن نیز پیدا کرد. در این نوشتار آموزشی ریاضی پایه دهم تمامی روشهای حل معادله درجه دوم را یاد گرفتیم. با تمام این روشها آشنا شده و از هر کدام چند مثال با یکدیگر حل کردیم.
در صورتیکه که هر سوالی از این بخش دارید، میتوانید در قسمت دیدگاهها در زیر همین پست سوال خود را مطرح کنید. ما در ریاضیکا به سوالات شما پاسخ میدهیم.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!





خیلی محتوای کاملی بود. تشکر
سلام بر شما دوست عزیز.
با تشکر از توجهتان به این پست.
ممنون از نظر قشنگتان.
واقعا ممنون اگر تمام سیستم تدریس کشور این طور مطلب رو باز وقابل فهم برای دانش اموزها توضیج بدن سطح سواد تو مملکت انقدر پایین نبود وتمیز تر در مورد :اگر a+c=-b انگاه یه جواب 1-وجواب دیگه c/a- بازم ممنون
ضمن عرض سلام و احترام
خیلی خوشحالیم که مطلب براتون مفید بوده
چنین کامنتی انرژی مارو برای ادامه مسیر دو چندان میکنه
موفق و پیروز باشید
سلام کارتون عالیه .اینستا تونو بدید برام تو ایمیلم مرسی استاد
سلام خیلی ممنون از توضیح عالیتون
من برای فهمیدن یه مطلب بسیار پیش پا افتاده چند سایت رو گشتم ولی انقدر پیچیده گفته بود که هیچی دستگیرم نشد بسیار ساده و روان توضیح دادید ممنون
عرض سلام و ادب
بسیار از شما دوست عزیز سپاسگزاریم که برای ادامه مسیر انرژی ما رو دو چندان میکنید.
موفق و پیروز باشید.
روش ریشه گیری جالب بودش
بهش توجه نکرده بودم
ممنونم????
خواهش میکنم دوست عزیز
سوالی داشتید میتونید بپرسید بهتون جواب بدیم ??
عالی وجامع بود
ضمن عرض سلام
سپاسگزاریم از لطف شما دوست عزیز
خوب نبود
ضمن عرض سلام و احترام
خوشحال میشیم که نکات منفی این متن که به نظرتون خوب نبوده رو برامون بنویسید.
سلام عالی بود و کاربردی مطالبق بر مطالب کتاب لطفا ویدیو شو بذارید.
سلام ممنون از انرژی که دادید. حتما ویدیشو تا آخر این ماه میگذاریم.
عالی بود من برای امتحان ریاضی واقعا به کمک نیاز داشتم ممنونم????????
سلام دوست عزیز.
ممنون از انرژی خوبتون.
موفق باشید.
خیلی کامل و خوب آموزش دادین . عالی بود
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون.
موفق باشید.
سلام
سلام و عرض ادب
بفرمایید.
سلام و خداقوت
درانتها که چند نکته و ثال آوردید به نظرم ایراد داره
ببینید درست میگم؟
ایکس به توان دو به اضافه هفت ایکس مساوی با دوازده
جمله سی مساوی با منفی دوازده باید بشه
شما نوشتید جمله سی مساوی مثبت دوازده؟!
ممنون میشم برام ایمیل کنید
یا سلام وعرض ادب
ممنون از توجه ودقت نظر شما در واقع مساوی ۱۲- بود که تصحیح شد
پیج ما رو در اینستا هم به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام روش تستی رو میشه توضیح بدید
با سلام واحترام
منظورتون از روش تستی چی هست؟
سلام اگه یه معادله درجه ۲ رو از روش دلتا و مربع کامل بریم از جفتش به سه جواب میرسیم؟
برا این میپرسم چون من از مربع کامل میرم به یه چیز دگ میرسم شاید دارم اشتباه میرم
لطفا راهنمایی کنید
سلام دوست عزیز
از هر راهی برید به جوابهای یکسان میرسید راهتون رو دوباره بررسی کنید واشکال کاررو پیدا کنید
سلام میخواستم بدونم حل معادله درجه ۳ ب صورت سواله 5+5x+x^2چطوری حل میشه اگه میشه لطفا راهنماییم کنید ممنون میشم
با سلام واحترام دوست عزیز این مثال درجه دوم هست واصلا معادله نیست وعبارت جبری هست در ضمن حل معادله درجه سوم قانونمند نیست یه روش تجزیه هست یه روش اینه با حدس گمان یکی از ربشه ها رو پیدا کنید سپس با اون ریشه وتجزیه لقیه ریشه ها رو بدست بیارید مثلا یک یا دو یا منفی یک رو بذارید به جای ابکس ببینید صفر میسه یا نه بعد اگه مثلا یک جواب داد یبه ایکس منهای یک عبارت ذو تفسیم کنید
سلام،بسیار ممنون از مطالب مفید و پرمحتوای شما. ببخشید روشی که در بعضی سوالات روش خوارزمی نامیده میشه کدوم هست؟؟؟!!!
با سلام وادب
همون روش مریع کامل هست
سلا بسیار عالی بود ،سپاس ازتون?
با سلام
ممنون از نظر شما
سلام تو قسمت مجموع ضرایب برایر 0 اون معادله جواب دوم 3 نیست و 3- هستش و با c/a هم بدست میاد
با سلام
ممنون از توجه شما
سلام و خداقوت خیلی عالی محتوای کامل و با حل مثال های زیاد من که عشق میکنم با سایتتون ریاضی برام شده اسون ترین درس مرسی
با سلام دوست عزیز
واقعا با خوندن نظرتون شارژ شدیم برای ادامه راه التماس دعا
در چه صورتی معادله درجه دوم جواب نداره؟؟!!
یا چه زمانی معادله درجه دوم جوابی نخواهد داشت؟
با سلام
وقتی دلتا منفی شود
ممنونم برای محتواتون خیلی کمک کننده بود?
با سلام دوست عزیز
ممنون از نظر لطف شما
با سلام ببخشید در قسمت تجزیه کردن سوال :
X² =4(x – 4)
–> X² – 4x + 4 = 0
قسمت c مثبت ۱۶ میشه
والا من دنبال ی روش فوق الاده راحت و تستی بودم اما تو هیچ سایتی نیست
این روش و استادم گفته بودن اما یادم رفته و دنبالش در ب در میگردم
ما همه روشها روگفتیم
سلام واحترام من مادر دانش اموز پایه دهم تجربی هستم وبعد از ۳۰سال باخوندن محتوای اموزشی شما تونستم به فرزندم کمک کنم خیلی سپاسگزارم موفق باشید خداقوت خیلی عالی
سلام به شما مادر کوشا
خوشحالیم که برای شما مفید بوده