آموزش ریاضی پایه دهم
اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
در سال نهم شما با آموزش اتحادهای جبری آشنا شدید و 4 تا از مهمترین آنها را یاد گرفتید. در سال دهم شما با 2 تا دیگر از اتحادهای جبری آشنا میشوید و تجزیه آنها را نیز یاد میگیرید. ابتدا به یادآوری این مبحث از سال نهم میپردازیم. قبل از آن تعریف اتحادهای جبری را برای شما یادآوری میکنیم.
وقتی دو عبارت جبری داریم که به ازای هر مقدار که به جای متغیرهای موجود قرار دهیم این دو عبارت با هم برابر باشند، گفته میشود که این دو عبارت با هم متحد هستند و یک اتحاد جبری را تشکیل میدهند. به مثال زیر دقت کنید:
\( \LARGE (x + 1)^2 = x^2 + 2x +1 \)
اگر به جای \( \Large x \) در دو طرف این تساوی هر عدد دلخواهی قرار دهیم آن دو با هم برابر خواهند شد. مثلاً به جای \( \Large x \) عدد 2 را قرار میدهیم و داریم:
\( \LARGE \begin{cases} (2 + 1)^2 = 3^2 = 9 \\ 2^2 + 2 \times 2 +1 = 9 \\ \end{cases} \)
\( \LARGE \rightarrow 9 = 9 \)
پس طرف اول و دوم با هم برابر است. به ازای هر مقدار \( \Large x \) این تساوی برقرار است. پس این دو با هم متحد هستند. حال به عبارت زیر دقت کنید:
\( \LARGE (a+b)^2 \neq a^2 + b^2 \)
اگر به جای \( \Large a , b \) مقادیر دلخواه قرار دهیم، هیچگاه دو طرف تساوی برابر نخواهند شد. مثلاً \( \Large b = 3 , a = 2 \) داریم:
\( \LARGE \begin{cases} (2 + 3)^2 = 5^2 = 25 \\ 2^2 + 3^2 = 4 + 9 = 13 \\ \end{cases} \)
\( \LARGE \rightarrow 25 \neq 13 \)
پس طرف اول و دوم با هم برابر نیستند. در نتیجه اینها با هم متحد نیستند و یک اتحاد جبری را تشکیل نمیدهند.
در ریاضیات یکسری اتحادهای مهم و کاربردی داریم که بهتر است آنها را فراگیریم و در درسهای آینده و در حل معادلات از آنها استفاده کنیم. در واقع روشهای سریع پیدا کردن طرف دوم اتحاد را میآموزیم. بدون انجام دادن عملیات طولانی! البته میتوانید از روشهای طولانی هم استفاده کنید ولی زمانبر خواهد بود.
اتحادهای جبری: اتحاد مریع دوجملهای
هرگاه یک دو جملهای جبری به توان دو برسد خواهیم داشت:
\( \LARGE (a+b)^2 \)
\( \LARGE = (a+b)(a+b) \)
\( \LARGE = a^2 + ab + ba + b^2 \)
\( \LARGE = a^2 + 2ab + b^2 \)
پس نتیجه میگیریم در عبارت زیر با هم متحد هستند.
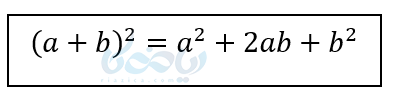
یا به عبارتی وقتی یک دوجملهای به توان دو میرسد در واقع داریم:

مثال ۱:
\( \LARGE (2x + 3z)^2 \)
\( \LARGE = 4x^2 + 12xz + 9z^2 \)
نکته ۱: اگر بین دو جمله منفی باشد داریم.
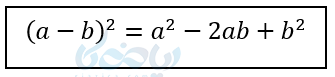
مثال ۲:
\( \LARGE (3xy – 1)^2 \)
\( \LARGE = 9x^{2}y – 6xy + 1 \)
نکته ۲: اگر هر دو منفی باشند داریم.
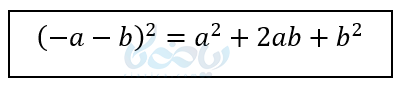
مثال ۳:
\( \LARGE (-a^{2}-3b)^2 \)
\( \LARGE = a^4 + 6a^{2}b + 9b^2 \)
اتحادهای جبری: اتحاد مزدوج
وقتی دو «دوجملهای» داشته باشیم که یک جمله آنها مساوی بود و جمله دیگر قرینه هم باشند، میگوییم این دو «دوجملهای» با هم مزدوج هستند. مانند:
\( \LARGE a+b , a-b \)
یا
\( \LARGE -z+b , z+b \)
دقت کنید وقتی دو، دوجملهای داشته باشیم که هر دوجملهها قرینه یکدیگر باشند در اینصورت میگوییم آنها با هم قرینهانداما مزدوج نمیباشند. مانند:
\( \LARGE a-b , -a+b \)
یا
\( \LARGE a+b , -a-b \)
حال اگر دو، دوجملهای مزدوج در هم ضرب شوند، داریم:
\( \LARGE (a+b)(a-b) \)
\( \LARGE = a^2 – ab + ba – b^2 \)
\( \LARGE = a^2 – b^2 \)
پس نتیجه میگیریم:
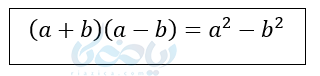
مثال ۴:
(1
\( \LARGE (2x-z)(2x+z) \)
\( \LARGE = 4x^2 – z^2 \)
(2
\( \LARGE (a^2 + 2b)(2b – a^2) \)
\( \LARGE = 4b^2 – a^4 \)
(3
\( \LARGE (5z-2)(2+5z) \)
\( \LARGE = 25z^2 – 4 \)
اتحادهای جبری: اتحاد جمله مشترک
وقتی دو، دوجملهای در هم ضرب شوند که فقط یک جمله آنها یکی و هم علامت باشد به اصطلاح مشترک باشد، میگوییم اینها با هم اتحاد جمله مشترک برقرار کردهاند و داریم:
\( \LARGE (x+a)(x+b) \)
\( \LARGE = x^2 + xb + ax +ab \)
\( \LARGE = x^2 + (a+b)x + ab \)
پس داریم:
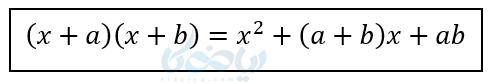
به عبارتی وقتی در اتحاد جمله مشترک داریم خواهیم داشت:

به مثالهای زیر دقت کنید:
(1
\( \LARGE (2a+3)(2a+4) \)
\( \LARGE = 4a^2 + 14a + 12 \)
(2
\( \LARGE (x^2 – 2y)(x^2 – 3y) \)
\( \LARGE = x^4 -5yx^2 + 6y^2 \)
(3
\( \LARGE (2x-1)(2x+3) \)
\( \LARGE = 4x^2 + 4x – 3 \)
(4
\( \LARGE (7 – 3xy)(8-3xy) \)
\( \LARGE = 9x^{2}y^2 -45xy+56 \)
اتحاد های جبری: اتحاد مربع سه جملهای
وقتی یک سهجملهای به توان دو برسد داریم:
\( \LARGE (a+b+c)^2 \)
\( \LARGE = (a+b+c)(a+b+c) \)
\( \LARGE = a^2 + ab + ac + ba + b^2 \)
\( \LARGE + bc + ac + bc + c^2 \)
\( \LARGE = a^2 + b^2 + c^2 \)
\( \LARGE + 2ab + 2ac + 2bc \)
یعنی:
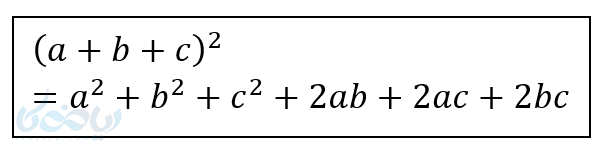
یعنی وقتی یک سهجملهای به توان 2 میرسد، ابتدا مربع هر کدام از جملات را نوشته سپس 2 برابر اولی در دومی و سومی ضرب شده و بعد دو برابر دومی در سومی.
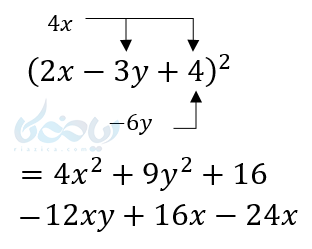
علامت جملات را همه با توجه به علامت جملات اولیه محاسبه میکنیم:

این روش را برای هر چند جملهای که به توان 2 میرسد میتوان به کاربرد:
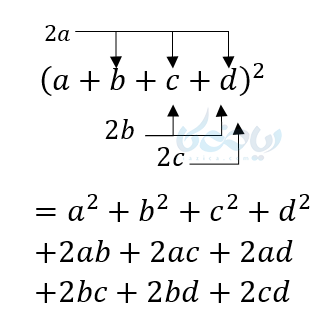
و همیشه تعداد جملات دو برابر تعداد جملات اولیه میشود. به این اتحاد اتحاد لاگرانژ نیز گفته میشود.
اتحادهای جبری بالا را شما در پایه نهم خواندید و با تجزیه آنها نیز آشنا شدید. حال میخواهیم به اتحادهایی که در پایه دهم میخوانید اشاره کنیم.
اتحاد های جبری : اتحاد مکعب دوجملهای
وقتی یک دوجملهای جبری به توان 3 برسد خواهیم داشت:
\( \LARGE (a+b)^3 \)
\( \LARGE = (a+b)^{2} (a+b) \)
\( \LARGE = (a^{2}+2ab + b^{2}) (a+b) \)
\( \LARGE = a^3 + a^{2}b+ 2a^{2}b \)
\( \LARGE + 2ab^2 + b^{2}a + b^3 \)
\( \LARGE = a^3 +3 a^{2}b+ 3ab^2 + b^3 \)
پس داریم:
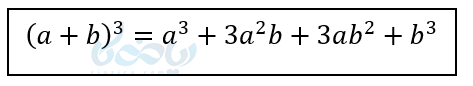
به زبان سادهتر در اتحاد مکعب دوجملهای داریم:

اگر بین دوجمله منها باشد داریم:
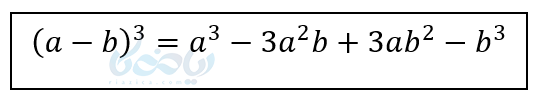
و اگر هر دوجمله منفی باشند:
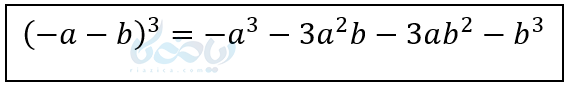
به مثالهای زیر دقت کنید:
(1
\( \LARGE (x+1)^3 \)
\( \LARGE = x^3 + 3x^2 + 3x +1 \)
(2
\( \LARGE (2a-3b)^3 \)
\( \LARGE = 8a^3 – 36a^{2}b \)
\( \LARGE + 54ab^2 – 27b^3 \)
از ترفند زیر برای نوشتن دوجمله وسط میتوانید استفاده کنید:
(1
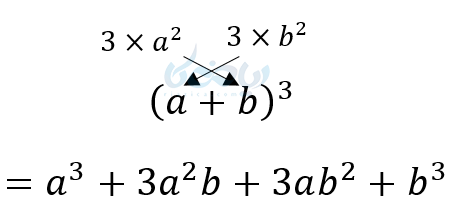
(2
(3
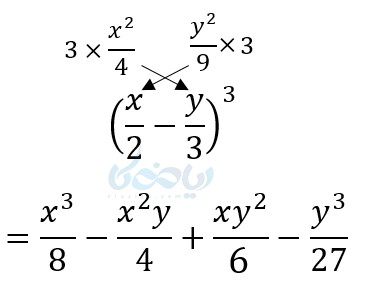
اتحادهای جبری: اتحاد مجموع یا تفاضل مکعبات دوجملهای معروف به چاق و لاغر
این اتحاد مانند اتحاد مزدوج اتحاد راحت و زیبایی است که به راحتی میتوانید بیاموزید. هرگاه یک دوجملهای در یک سهجملهای ضرب شود، به صورتی که سهجملهای دارای یک ارتباط ویژه با دوجملهای باشد، به این اتحاد، اتحاد چاق و لاغر میگوییم. دقت کنید:

همانطور که میبینید اولین جمله سهجملهای مربع جمله اول، دومین جمله قرینه حاصلضرب دو جمله و سومین جمله سهجملهای ،مربع جمله دوم است. در اینصورت داریم:
\( \LARGE (a+b)(a^2 -ab + b^2) \)
\( \LARGE = a^3 – a^{2}b + ab^2 \)
\( \LARGE + ba^2 -ab^2 + b^3 \)
\( \LARGE = a^3 + b^3 \)
یعنی داریم:
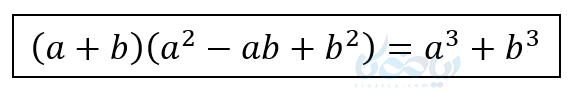
و به همین ترتیب خواهیم داشت:
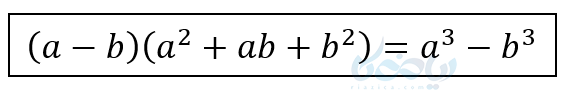
یعنی برای نوشتن جواب:
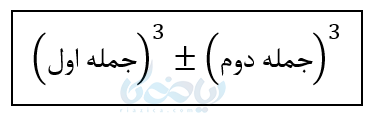
برای همین اسم اصلی این اتحاد مجموع یا تفاضل مکعبات دوجملهای است. یعنی اسم آن از روی جواب این اتحاد گرفته شده است. ولی برای سهولت به آن اتحاد چاق و لاغر یا فیل و فنجان هم میگویند.
نکته ۳: حاصلضرب هر دوجملهای در هر سهجملهای اتحاد چاق و لاغر نیست.
به مثالهای زیر دقت کنید:
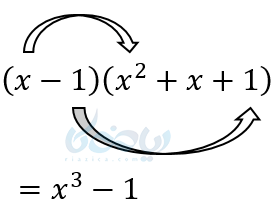
در واقع ما هر جمله را در مربع خودش ضرب میکنیم و از ضرب کردن بقیه جملات خودداری میکنیم. چون میدانیم جملات دیگر قرینه هستند و از بین میروند.
(1
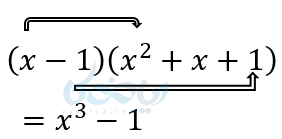
(2
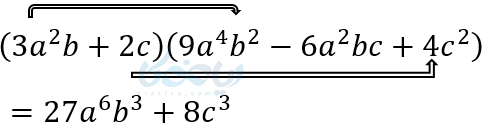
(3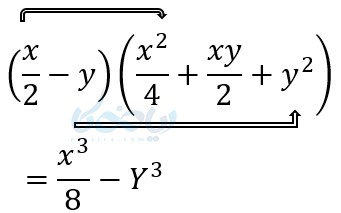
به مثالهای زیر دقت کنید. چون از این نکته در آینده برای گویا کردن مخرج کسرهای رادیکالی استفاده میکنیم.
(4
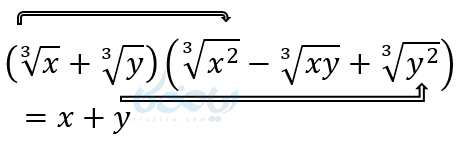
(5
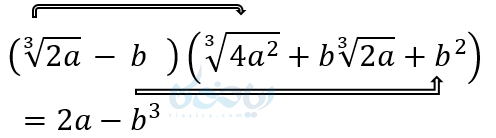
قبل از خوندن این پست درسنامه اتحاد ریاضی نهم را حتما مطالعه فرمایید.
ویدیو از اتحادهای جبری 6رابطه داغ داغ
در این ویدیو با حل چند نمونه سوال اتحادهای جبری بیشتر توضیح داده شده است
زنگ آخر درس اتحادهای جبری
در این نوشتار باهم یک مبحث شیرین دیگر از آموزش ریاضی دهم، یعنی اتحادهای جبری را یاد گرفتیم. همچنین مثالهای متعدد همراه با فرمول تمامی آنها را نیز باهم دوره کردیم. در رابطه با درس تجزیه عبارت های جبری نیز مطالب مفید دیگری در سایت ریاضیکا قرار داده شده است.
در صورتیکه که هر سوالی از این مبحث داشتید، سوال خود را زیر همین نوشتار در بخش دیدگاهها برای ما بنویسید. ما در ریاضیکا به سوالات شما پاسخ خواهیم داد.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!



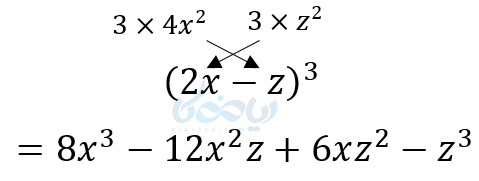


سلام به شدت عالی بودش.
سلام دوست عزیز ممنون از انرژی که میدید.
تا حالا با خوندن چیزی اینقدر نفهمیده بودم عالی بود
ببخشید 3 سوال برام به وجود اومده میشه بگید با چه اتحاد هایی ساده میشن؟؟
سلام و عرض ادب ممنون از مفید بودن مطالب جواب سوالاتتون رو با خوندن پست تجزیه مبگیرید.
https://riazica.com/factorization-of-expressions/
X^2 + 3x + 2
و
X^3 + X^2 + X + 1
و
X^5 + X + 1
ممنون؟???
سلام و عرض ادب ممنون از مفید بودن مطالب جواب سوالاتتون رو با خوندن پست تجزیه مبگیرید.
https://riazica.com/factorization-of-expressions/
البته این دو نظر رو باید در مبحث بعدی یعنی تجزیه اتحاد ها میدادم اما خب مشتاق شدم که مطالب دیگه تونو بخونم و اومدم اینجا و وقتی تموم شد اینجا داد
سلام و عرض ادب ممنون از مفید بودن مطالب جواب سوالاتتون رو با خوندن پست تجزیه مبگیرید.
https://riazica.com/factorization-of-expressions/
فوقالعاده بود
سلام دوست عزیز
خوشحالیم که براتون مفید بوده
اینا فوقالعاده عالی هستن
اما مطالب پایه یازدهم را از کجا میتونم بهشون دسترسی داشته باشم؟
با سلام واحترام
در صفحه اصلی بزنید روی آموزش ریاضی بزنید تمام آموزشهای پایه های مختلف رو ببینید
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام.ممنون از مطالب آموزندتون.فقط در جواب مثال دوم مکعب دو جملهای.
(2a-3b)
علامت جمله آخر باید منفی باشد.با تشکر.
با سلام
ممنون از دقت نظر ما اصلاح شد
خیلی عالی،واضح و مفید بود.کاملا متوجه شدم ?
با سلام وادب
ممنون از نظر لطف شما
بی نظیر و عالی بود ❣️
با سلام دوست عزیز
ممنون از نظر محبت آمیز شما
خیلی ممنون واقفا عالی بود
ممنون از نگاه شما