صفر تا صد توان‌ های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!

در این بخش می‌خواهیم به مفهوم توان‌ های گویا بپردازیم اما قبل از آن توان طبیعی، صفر، صحیح منفی را بیان کرده سپس به توان گویا می‌پردازیم.

توان طبیعی

توان یک مفهوم ساده ودر عین حال کاربردی ریاضیات می باشد.مفهوم توان به زبان ساده به  این صورت بیان می شود که وقتی عددی چند بار در خودش ضرب شود، عدد مورد نظر (پایه) را نوشته وتعداد دفعاتی که در خودش ضرب شده را بالای آن می‌نویسیم (توان یا نما) .در واقع می‌توان برای سادگی و راحتی در نوشتن ومحاسبه سریع از تکنیک توان و قوانین آن استفاده کرد. بله توان یک تکنیک برای ساده‌نویسی است نه یک عمل. منظور از عمل، عملیات‌های جمع و تفریق و ضرب و تقسیم است.

مثال ۱:

 

حال می‌خواهیم به شما بگوییم که این تعریف در اصل مربوط به تعریف توان طبیعی است. وقتی می‌گوییم \( \Large n \in \mathbb{N}  , a^n   \) یعنی \( \Large a   \) را \( \Large n   \) بار در خودش ضرب می‌کنیم.

اما توان صفر، صحیح منفی و گویا و اصم تعاریف دیگری دارند که در ادامه برای شما بیان خواهیم کرد. قبل از آن به قوانینی که در مورد توان طبیعی وجود دارد و شما نیز با آن‌ها آشنا هستید اشاره خواهیم کرد.

---

---

قوانین توان طبیعی

توان‌ های گویا :‌ توان صفر

همانطور که در بالا در مورد قوانین توان خواندیم، اگر دو عدد توان‌دار با توان‌های طبیعی به هم تقسیم شوند که پایه‌ها با هم برابر باشند، یکی از پایه‌ها را نوشته و توان‌ها را کم می‌کنیم. حال به مطالب زیر دقت کنید.

\( \LARGE \frac{a^n}{a^n} = a^{n-n} = a^0 (1)  \)

از طرفی وقتی دو عدد برابر به هم تقسیم شوند، حاصل برابر یک می‌شود. پس داریم:

\( \LARGE \frac{a^n}{a^n} = 1 (2)  \)

از 1 و 2 نتیجه می‌گیریم:

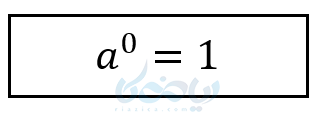
پس، نتیجه می‌گیریم:

اگر دقت کنید می‌بینید تعریف توان صفر با توان طبیعی کاملاً متفاوت شد.

مثال ۲: عبارت‌های زیر را حل کنید.

(1

\( \LARGE 5^0 = ?  \)

حل:

\( \LARGE 5^0 = 1  \)
(2

\( \LARGE (\frac{1}{2})^0 = ?  \)

حل:

\( \LARGE (\frac{1}{2})^0 = 1  \)
(3

\( \LARGE (\sqrt5)^0 = ?  \)

حل:

\( \LARGE (\sqrt5)^0 = 1  \)
(4

\( \LARGE (a^{2}b^{3}c^{4} )^0 = ?  \)

حل:

\( \LARGE (a^{2}b^{3}c^{4} )^0 = 1  \)

 

توان های گویا : توان صحیح منفی یا توان منفی

برای تعریف منفی، یکبار دیگر از توان طبیعی و قوانین آن کمک می‌گیریم. فرض کنید \( \Large n , m  \) دو عدد طبیعی باشند که \( \Large n < m   \) . همچنین رابطه \( \Large m – n = r   \) بین آن‌ها برقرار باشد. در نهایت داریم:

\( \LARGE \frac{a^n}{a^m} = a^{n-m} = a^{-r} (1)  \)

از طرفی:

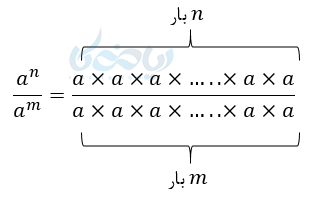
اگر در این کسر شروع به ساده کردن \( \Large a   \) های بالا و پایین کنیم در نهایت صورت یک و در مخرج به اندازه \( \Large m – n \) تا  \( \Large a  \)داریم، یعنی:

\( \LARGE \frac{a^n}{a^m} = \frac{1}{a^{m-n}} = \frac{1}{a^r} (2)  \)

از 1 و 2 نتیجه می‌گیریم:

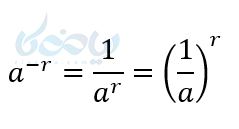
به زبان ساده یعنی وقتی عددی حقیقی به توان عدد منفی می‌رسد و بخواهیم مقدار آن را پیدا کنیم، پایه معکوس و توان مثبت می‌شود. حال این مفهوم را با یک مثال برای شما بار دیگر بیان می‌کنم.

مثال ۳: مقدار \( \Large 5^{-4} \) را حساب کنید.

حل: فرض کنید داریم، \( \Large \frac{5^5}{5^9} = 5^{-4}   \)

از طرفی:

همانطور که دیدید لزوماً توان منفی، مقداری منفی نمی‌شود و بسته به پایه مقدار‌های مختلفی می‌شود. مثلاً اگر پایه عدد طبیعی بزرگتر از یک باشد، توان‌های منفی آن اعدادی مثبت بین صفر و یک خواهد بود. مانند \( \Large 5^{-4} \). به مثال‌های زیر دقت کنید تا مفهوم توان منفی برای شما روشن‌تر شود.

مثال ۴: مقادیر زیر را بدست آورید.

(1

\( \LARGE 3^{-4} = ?  \)

حل:

\( \LARGE 3^{-4} = (\frac{1}{3})^{4} = \frac{1}{81} \)

(2

\( \LARGE (\frac{1}{2})^{-5} = ?  \)

حل:

\( \LARGE (\frac{1}{2})^{-5} = 2^5 = 32  \)

(3

\( \LARGE (-5)^{-2} = ?  \)

حل:

\( \LARGE (-5)^{-2} = (-\frac{1}{5})^{2} = \frac{1}{25}   \)

(4

\( \LARGE (-\frac{1}{3})^{-5} = ?  \)

حل:

\( \LARGE (-\frac{1}{3})^{-5}  \)

\( \LARGE = (-3)^{5} = -243 \)

(5

\( \LARGE (\frac{7}{2})^{-3} = ?  \)

حل:

\( \LARGE (\frac{7}{2})^{-3} = (\frac{2}{7})^{3} = \frac{8}{343}  \)

(6

\( \LARGE (0.3)^{-4} = ?  \)

حل:

\( \LARGE (0.3)^{-4} = (\frac{3}{10})^{-4}   \)

\( \LARGE  = (\frac{10}{3})^{4} = \frac{10000}{81}  \)

(7

\( \LARGE \frac{1}{5^{-2}} = ?  \)

حل:

\( \LARGE \frac{1}{5^{-2}} = 5^2 = 25  \)

(8

\( \LARGE \frac{5^3}{5^{-2}} = ?  \)

حل:

\( \LARGE \frac{5^3}{5^{-2}} = 5^3 \times 5^2 = 5^5  \)

(9

\( \LARGE \frac{4^3}{3^{-3}} = ?  \)

حل:

\( \LARGE \frac{4^3}{3^{-3}} = 4^3 \times 3^{3} = 12^3  \)

 

نکته ۱: تمام قوانین توان‌ ها که در مورد توان طبیعی بیان کردیم، در مورد توان‌های منفی نیز برقرار است که ما از اثبات آنها خودداری می‌کنیم.
به مثال‌های زیر دقت کنید:

(1

\( \LARGE 5^{-2} \times 5^{-3} = ?  \)

حل:

\( \LARGE 5^{-2} \times 5^{-3}  \)

\( \LARGE  = 5^{-5} = \frac{1}{5^5} \)

(2

\( \LARGE 3^{-7} \times 4^{-7} = ?  \)

حل:

\( \LARGE 3^{-7} \times 4^{-7}  \)

\( \LARGE  = 12^{-7} = \frac{1}{12^7}  \)

(3

\( \LARGE \frac{5^{-4}}{5^{-2}} = ?  \)

حل:

\( \LARGE \frac{5^{-4}}{5^{-2}} = 5^{-2} = \frac{1}{5^2}  \)

(4

\( \LARGE \frac{7^{-5}}{3^{-5}} = ?  \)

حل:

\( \LARGE \frac{7^{-5}}{3^{-5}} \)

\( \LARGE = (\frac{7}{3})^{-5} = (\frac{3}{7})^{5} \)

(5

\( \LARGE (4^{-2})^3 = ?  \)

حل:

\( \LARGE (4^{-2})^3 = 4^{-6} = \frac{1}{4^6}  \)

(6

\( \LARGE \frac{3^4 \times 4^{-2}}{2^{-3} \times 9^2} = ?  \)

حل:

\( \LARGE \frac{3^4 \times 2^{-4}}{2^{-3} \times 3^4}  \)

\( \LARGE = 2^{-1} = \frac{1}{2}  \)

(7

\( \LARGE 5^{-7} \times 3^{-4} \times 5^5 \times 3^4 = ?  \)

حل:

\( \LARGE 5^{-2} \times 3^0  \)

\( \LARGE = (\frac{1}{5})^2  \)

(8

\( \LARGE 8^{-2} \times 2^3 = ?  \)

حل:

\( \LARGE 8^{-2} \times 2^3  \)

\( \LARGE = (2^3)^{-2} \times 2^3  \)

\( \LARGE = 2^{-6} \times 2^3   \)

\( \LARGE = 2^{-3} = (\frac{1}{2})^3   \)

---

---

توان‌ های گویا

آزمایشگاهی را در نظر بگیرید که در آن دانشمندان بر روی باکتری‌ها تحقیق می‌کنند. در آزمایشی یک نوع باکتری کشت داده شده که در شرایط مساعد وزن این باکتری‌ها در هر ساعت دو برابر می‌شود. اگر وزن آن‌ها در شروع آزمایش یک گرم باشد، وزن آن‌ها بعد از یک ساعت 2 گرم و بعد از دوساعت 4 گرم و ….. خواهد شد. یعنی داریم:

\( \LARGE 1 , 2 , 4 , 8 , ….   \)

\( \LARGE 2^0 , 2^1 , 2^2 , 2^3 , ……. 2^n \)

حال می‌خواهیم ببینیم وزن این باکتری‌ها بعد از نیم ساعت یا همان \( \Large \frac{1}{2} \) ساعت چقدر می‌شود. اگر فرض کنیم بعد از نیم ساعت وزن باکتری‌ها \( \Large b \) برابر شود، طبق الگوی دنباله بالا وزن باکتری‌ها باید \( \Large b = 2^{\frac{1}{2}} (1) \) شود. اما این سوال پیش می‌آید که مقدار این عدد توان‌دار چقدر است؟

فرض کردیم وزن باکتری‌ها بعد از نیم ساعت \( \Large b \) برابر شود. در این صورت بعد از یک ساعت وزن آن‌ها \( \Large b \times b = b^2 \) خواهد بود. از طرفی طبق دنبالهٔ بالا بعد یک ساعت وزن باکتری‌ها 2 برابر خواهد شد. یعنی \( \Large b^2 = 2 \). خب پس داریم: \( \Large b = \sqrt2 (2) \)

از رابطه 1 و 2 به یک نتیجه جالب می‌رسیم:

\( \LARGE 2^{\frac{1}{2}} = \sqrt2 \)

به همین ترتیب می‌توان ثابت کرد:

\( \LARGE 3^{\frac{1}{4}} = \sqrt[4] {3} \)

\( \LARGE 5^{\frac{1}{7}} = \sqrt[7] {5} \)

و به طور کلی برای هر عدد مثبت حقیقی مانند \( \Large a   \) و هر عدد طبیعی بزرگتر از یک مانند \( \Large n  \) داریم:

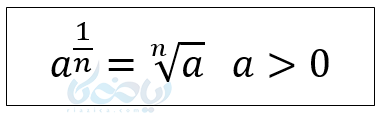
نکته ۲ در توان های گویا : \( \Large a \) را مثبت می‌گیریم چون اگر فرجه زوج باشد و \( \Large a \) منفی یک عبارت بی‌معنی به وجود می‌آید.

خب حال اگر صورت عددی غیر از یک باشد چه اتفاقی می‌افتد؟

فرض کنید \( \Large a^m \) بتوان \( \Large \frac{1}{n} \) برسد طبق تعریف بالا داریم:

\( \LARGE (a^m)^{\frac{1}{n}} = \sqrt[n] {a^m} (1) \)

از طرفی گفتیم دو توان متوالی در هم ضرب می‌شوند پس داریم:

\( \LARGE (a^m)^{\frac{1}{n}} = a^{\frac{m}{n}} (2) \)

از 1 و 2 نتیجه می‌گیریم:

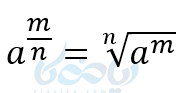
مثال ۴: عبارت‌های زیر به صورت رادیکالی بنویسید.

(1

\( \LARGE 3^{\frac{1}{7}} =? \)

حل:

\( \LARGE 3^{\frac{1}{7}} = \sqrt[7] {3} \)

(2

\( \LARGE 2^{\frac{3}{5}} =? \)

حل:

\( \LARGE 2^{\frac{3}{5}} = \sqrt[5] {2^3} \)

(3

\( \LARGE 5^{\frac{3}{4}} =? \)

حل:

\( \LARGE 5^{\frac{3}{4}} = \sqrt[4] {5^3} \)

نکته توان‌ های گویا: تمام قوانینی که در مورد توان‌ها طبیعی بیان کردیم در مورد توان‌ های گویا نیز برقرار است.

نکته مهم توان‌ های گویا: نتیجه می‌گیریم که هر توان گویا هر عدد به صورت یک ریشه‌گیری بیان می‌شود و ریشه تقریبی یا کامل آن عدد مقدار آن توان گویا خواهد بود. مثلا:

\( \LARGE 2^{\frac{1}{2}} = \sqrt2  \simeq 1.4 \)

قوانین توان‌ های گویا

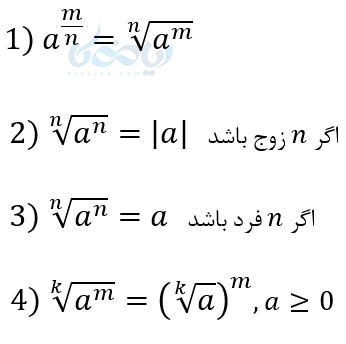
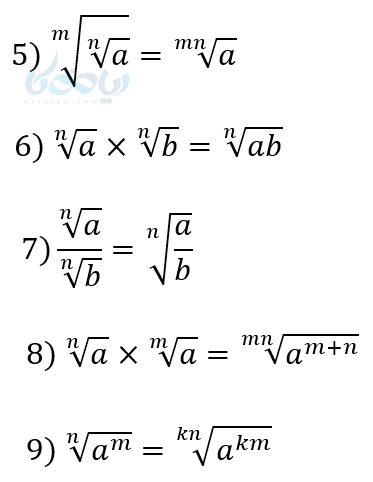
اثبات بعضی از قوانین توان‌ های گویا

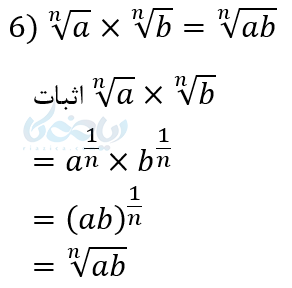
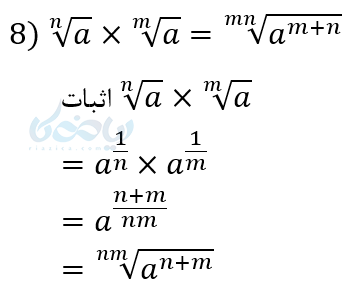
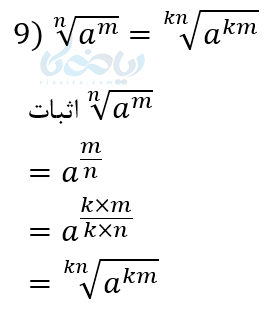
چند مثال از توان‌ های گویا برای فهم بهتر

مثال ۵ از توان‌ های گویا: عبارت‌های زیر را ساده کنید و به صورت یک رادیکال بنویسید.

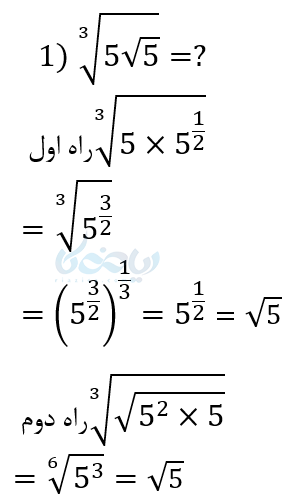
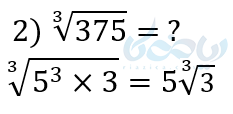
توضیح قسمت ۲ از مثال ۵:
در چنین نمونه‌هایی عدد زیر رادیکال را تجزیه کرده و سپس ساده می‌کنیم.

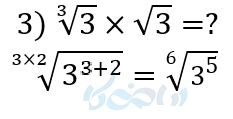
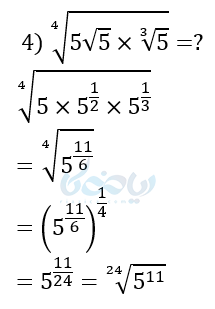
توان گنگ

شاید این سوال برایتان پیش بیاید که ما توان طبیعی، صفر، منفی و گویا را تعریف کردیم. اما آیا توان گنگ هم تعریف شده است؟

جواب مثبت است. توان گنگ را به صورت دنباله‌ای اعشاری تعریف می‌کنیم. ولی مثلاً \( \Large 2^{\sqrt2} \) را می‌خواهیم تعریف کنیم. می‌دانیم مقدار \( \Large \sqrt2 \) با چند رقم اعشار برابر با مقدار زیر است:

\( \Large \sqrt2 \simeq 1/41421356…. \)

پس دنبالهٔ اعشاری زیر به \( \Large \sqrt2 \) نزدیک و نزدیک‌تر می‌شود.

\( \LARGE 2^1 , 2^{1/4} , 2^{1/414} , …. , 2^{\sqrt2} \)

یعنی اعداد این دنباله به  \( \Large 2^{\sqrt2} \) میل می‌کنند. اگر جواب اعداد تواندار از بالا را تا سه رقم اعشار بنویسیم. داریم:

\( \LARGE 2 , 2/639 , 2/657 , … , 2^{\sqrt2}   \)

\( \LARGE  \simeq 2/665  \)

مثال ۶: \( \Large 3^{\pi} \) را تعریف کنید.

\( \LARGE \pi \simeq 3/14159265…. \)

\( \LARGE 3^1 , 3^{3/1} , 3^{3/14} , …  \)

\( \LARGE  \rightarrow 3^{\pi} \)

پس در کل نتیجه می‌گیریم که توان یک عدد، هر عدد حقیقی می‌تواند باشد.

\( \LARGE  y = a^x \)

\( \LARGE \rightarrow  \begin{cases} x \in \mathbb{R} \\ a \in \mathbb{R} \geq 0 \end{cases} \)

---

---

ویدیو از صفر تا صد توان های گویا

در این ویدیو دو نمونه سوال پر کاربرد از توان های گویا برای شما حل شده است

زنگ آخر کلاس توان های گویا

در این نوشتار مهم از مجموعهٔ آموزش ریاضی دهم ، با هم توان‌ های گویا را از پایه تا اثبات و قوانینش مطالعه کردیم. مطالب دیگری از آموزش ریاضی دهم را نیز می‌تونید در وب‌سایت ریاضیکا مطالعه کنید.

هرچی سوال از این نوشتار آموزشی داشتید، زیر همین قسمت در بخش دیدگاه‌ها برای ما بنویسید. کارشناسان ریاضیکا به سوال‌های شما پاسخ می‌دهند.

به خوندن ادامه بده!

متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞آموزش دنباله حسابی 🧮🔢 – از همیشه ساده‌تر؟