آموزش ریاضی پایه دهم
رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
رسم سهمی با روش انتقال همواره یکی از مباحث شیرین و البته مهم در آموزش ریاضی دهم بوده است. آنچه در این مبحث مهم است این است که تمام چندجملهایها جزء توابع هستند. از جمله سهجملهایهای درجه دوم که به فرم \( \Large y=ax^2 + bx+c \) هستند. ما قبلا با حل معادلات درجه دوم و رسم نمودار آنها (سهمی) آشنا شدهایم. پس معادلات درجه دوم جزء توابع هستند. چون به ازای هر \( \Large x \) فقط یک \( \Large y \) داریم.
بزرگترین دامنه ممکن توابع درجه دوم \( \Large \mathbb{R} \) است. ما با رسم این توابع در آموزش رسم نمودار سهمی آشنا شدیم. میتوانیم نمودار این توابع را هم به روش انتقال به همان صورت که در مورد تابع قدرمطلق گفتیم نیز رسم کنیم.
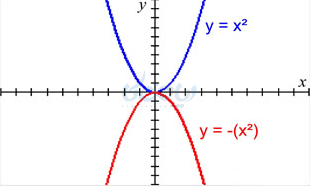
نمودار تابع درجه دوم ساده و قرینه اش به شکل زیر است.
انواع انتقال در رسم سهمی به روش انتقال
در حالت کلی بسته به معادله سهمی به دو جهت انتقال پیدا می کند:
- انتقال افقی
- انتقال عمودی
رسم سهمی به روش انتقال افقی
حال اگر در معادله سهمی \( \Large x \) از عددی مانند \( \Large h \) کم شود، اگر \( \Large h \) مثبت باشد نمودار به سمت راست و اگر منفی باشد به سمت چپ منتقل میشود. به زبان سادهتر اگر \( \Large x \) با عددی جمع شود نمودار به سمت چپ و اگر از عددی کم شود به سمت راست انتقال پیدا میکند.
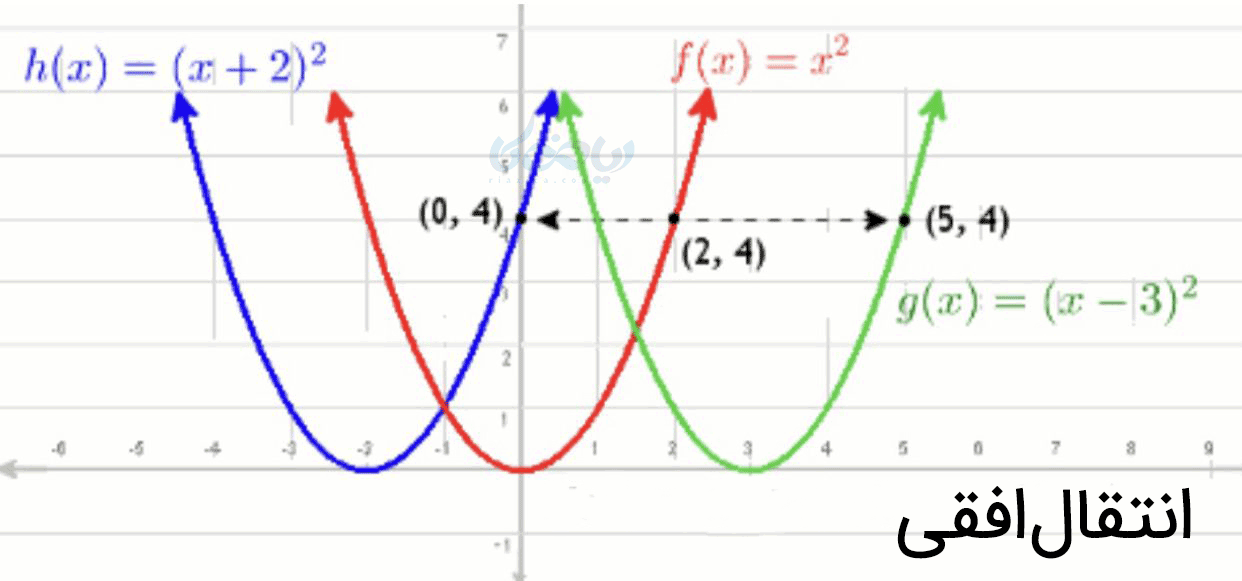
با داشتن نمودار تابع \( \Large f(x) \) میتوان نمودار تابع \( \Large f(x-h) \) را به روش انتقال رسم کرد.
اگر \( \Large h>0 \) باشد نمودار را \( \Large h \) واحد به سمت راست و اگر \( \Large h<0 \) باشد نمودار را \( \Large h \) واحد به سمت چپ منتقل میکنیم.
رسم سهمی به روش انتقال عمودی
حال فرض کنید خود تابع درجه دو بعلاوه عددی مانند \( \Large k \) شود. اگر \( \Large k \) مثبت باشد نمودار به بالا و اگر منفی باشد به پایین منتقل میشود.
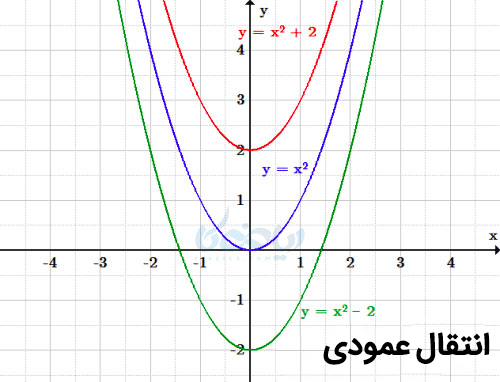
با داشتن نمودار \( \Large f(x) \) تابع میتوان نمودار تابع \( \Large f(x)+k \) را به روش انتقال رسم کرد.
اگر \( \Large k>0 \) باشد نمودار را \( \Large k \) واحد به سمت بالا و اگر \( \Large k<0 \) باشد نمودار را \( \Large k \) واحد به سمت پایین منتقل میکنیم.
اگر هم \( \Large x \) و هم تابع با مقادیری جمع یا کم شوند، هم انتقال عمودی و هم انتقال افقی خواهیم داشت. این حالت را در مثال زیر شرح دادهایم.
چند مثال از رسم سهمی به وش انتقال
مثال ۱: نمودار تابع \( \Large f(x)=(x-2)^2+3 \) را رسم کرده و دامنه و برد آن را تعیین کنید.
حل ۱: دقیقاً مانند تابع قدرمطلق رأس و دو نقطه کمکی را پیدا کرده و نمودار را رسم میکنیم. اما اگر بخواهیم به روش انتقال این کار را انجام دهیم، ابتدا نمودار تابع \( \Large f(x)=x^2 \) را رسم کرده سپس آن را دو واحد به راست و سه واحد به بالا منتقل میکنیم.
ریشه داخل پرانتز (\( \Large x \) رأس)
\( \LARGE x=2 \rightarrow y=3 \)
رأس \( \LARGE S:(2,3) \)
| 3 | 2 | 1 | x |
|---|---|---|---|
| 4 | 3 | 4 | y |
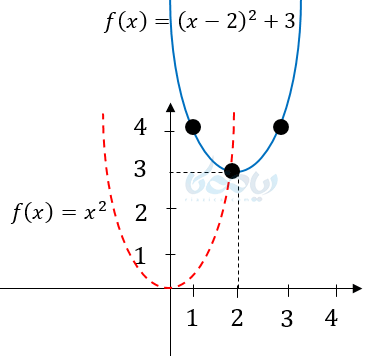
\( \LARGE D_f = \mathbb{R} \)
\( \LARGE R_f= [3,+\infty) \)
مثال ۲: نمودار تابع \( \Large f(x)=-(x+2)^2-1 \) را رسم کرده و دامنه و برد آن را تعیین کنید.
حل ۲: در این مثال باید ابتدا نمودار تابع \( \Large f(x)=-x^2 \) را رسم کنیم. سپس آن را دو واحد به چپ و یک واحد به پایین منتقل میکنیم.
ریشه داخل پرانتز (\( \Large x \) رأس)
\( \LARGE x=-2 \rightarrow y=-1 \)
راس \( \LARGE S:(-2,-1) \)
| -1 | -2 | -3 | x |
|---|---|---|---|
| -2 | -1 | -2 | y |
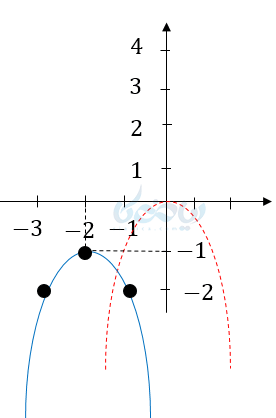
\( \LARGE D_f = \mathbb{R} \)
\( \LARGE R_f= (-\infty,-1] \)
مثال ۳: با توجه به نمودارهای رسم شده معادله توابع را بنویسید.
حل ۳:
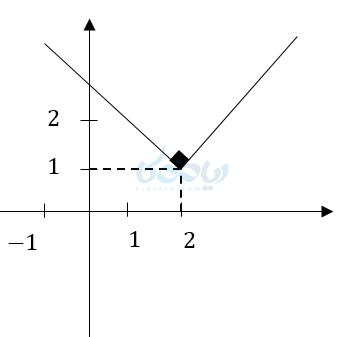
چون نمودار هفت است پس تابع قدرمطلق است. این نمودار دو واحد به راست و یک واحد به بالا منتقل شده. پس معادله آن \( \Large y=\left|x-2\right|+1 \) است.
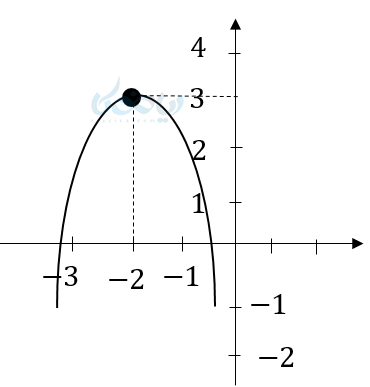
این نمودار سهمی است و رو به پایین که رأس آن سه واحد به بالا و دو واحد به چپ منتقل شده. پس معادله آن \( \Large y=-(x+2)^2+3 \) است.
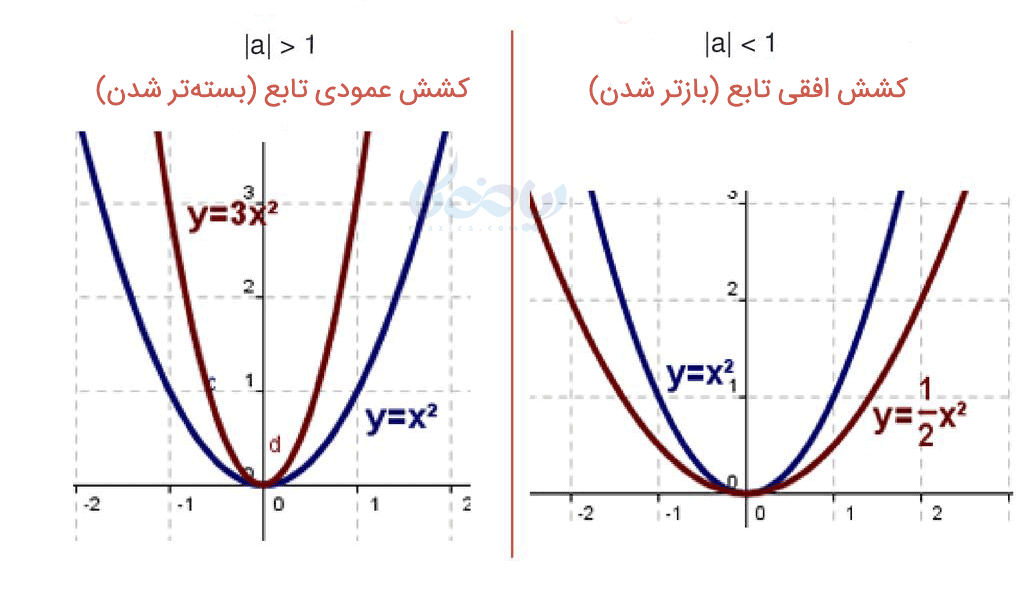
رسم نمودار به روش انتقال با وجود ضریب ثابت
در نظر بگیرید در تابع درجه دو \( \Large x \) یا خود تابع ضریبی مانند \( \Large a \) داشته باشند. اگر \( \Large \left|a\right|>1 \) باشد باعث کشش عمودی تابع (بستهتر شدن) نمودار میشود. همچنین اگر \( \Large\left|a\right|<1 \) باشد باعث کشش افقی تابع (بازتر شدن) دهانه نمودار میشود.
به طور کلی خلاصه رسم نمودار تابع درجه دو (سهمی) به روش انتقال به صورت زیر است:

زنگ آخر
در این نوشتار از مجموعه آموزش ریاضی دهم، باهم رسم سهمی به روش انتقال را فرا گرفتیم. حالتهای مختلف رسم سهمی به روش انتقال که شامل انتقال عمودی و انتقال افقی است را باهم دیدیم. همچنین مثالهای مختلفی را در این زمینه باهم حل کردیم و در آخر نیز رسم سهمی به روش انتقال را با وجود یک ضریب ثابت باهم بررسی کردیم.
در صورتیکه هرکدام از شما عزیزان سوالی در رابطه با این مبحث دارید، میتوانید در بخش دیدگاههای این نوشتار سوال خود را مطرح کنید. ما در ریاضیکا مشتاقیم که سوالات شما عزیزان را پاسخ دهیم.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!





درجه یک