آموزش احتمال دهم – کامل‌ترین و جامع‌ترین آموزش 🔣❓

گاهی اوقات قبل از شروع یک کار جدید یا شرکت در مسابقه یا قرعه کشی، لازم است میزان موفقیت خود را از قبل پیش بینی کنید تا تصمیمات درستی اتخاذ کنید. در اینجا است که آموزش احتمال دهم به ما کمک می‌کند تا شانس موفقیت خود را حدس بزنیم و با اطمینان گام برداریم.

---

---

تعاریف اولیه در آموزش احتمال دهم

قبل از شروع بحث لازم از ابتدا با چند اصطلاح ساده که در این درس بسیاز از آن‌ها استفاده خواهیم کرد آشنا شویم.

آزمایش تصادفی

آزمایشی که نتیجه آن از قبل مشخص نیست را آزمایش تصادفی می‌نامند. مانند پرتاب یک تاس، پرتاب یک سکه، بدنیا آمدن فرزند، قرعه‌کشی و …..

فضای نمونه

به مجموعه تمام نتایج ممکن یک آزمایش تصادفی فضای نمونه آزمایش گفته می‌شود. فضای نمونه را با \( \Large S \) و تعداد اعضای آن را با \( \Large n(S) \) نشان می‌دهند.

چند مثال مهم برای آموزش احتمال دهم

مثال ۱: فضای نمونه پرتاب یک تاس را بنویسید.

\( \LARGE S=\{1,2,3,4,5,6\} \)

\( \LARGE n(S)=6 \)

مثال ۲: فضای نمونه تولد یک فرزند و پرتاب یک سکه را بنویسید.

نکته احتمال دهم ۱: در مواقعی که آزمایش تصادفی ما از دو آزمایش تشکیل شده می‌توان به کمک جدول فضای نمونه را راحت‌تر نوشت.

مثال ۳: فضای نمونه پرتاب یک سکه و یک تاس را بنویسید.

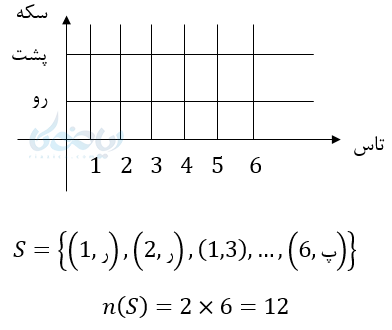
تعداد اعضای نمونه طبق اصل ضرب \( \Large 2 \times 6 \) خواهد شد.

نکته ۲: اگر تعداد فضای نمونه آزمایشی \( \Large m \) و تعداد فضای نمونه و آزمایش دیگری \( \Large n \) باشد، و هر دو آزمایش تصادفی با هم رخ دهند، تعداد فضای نمونه آن‌ها طبق اصل ضرب \( \Large m \times n \) خواهد بود.

\( \LARGE n(S)=m \times n \)

به همین ترتیب اگر چند آزمایش با فضای نمونه‌ای مختلف با هم رخ دهند، فضای نمونه جدید برابر حاصلضرب فضای نمونه هر یک خواهد بود.

\( \LARGE n(S)=m \times n \times … \times k \)

مثال ۴: فضای نمونه پرتاب دو تاس را بنویسید.

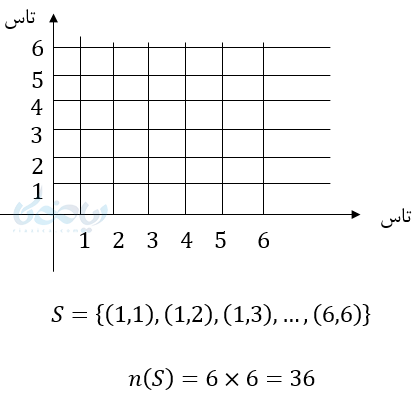
نکته ۳: اگر تعداد اعضای فضای نمونه آزمایشی \( \Large m \) باشد و آن آزمایش \( \Large K \) بار تکرار شود، تعداد اعضای نمونه فضای نمونه \( \Large m^K \) خواهد بود.

مثال ۵: سکه‌ای را 5 بار پرتاب می‌کنیم. تعداد اعضای فضای نمونه آن چند است؟

\( \LARGE n(S)=2^5=32 \)

مثال ۶: در کیسه 8 مهره متمایز وجود دارد. 3 مهره به تصادف خارج می‌کنیم. تعداد فضای نمونه این آزمایش چندتا است؟

\( \LARGE n(S)=\begin{pmatrix} 8\\ 3 \end{pmatrix} \)

\( \LARGE =\frac{8!}{5! \times 3!}=56 \)

نکته ۴: برای نوشتن فضای نمونه آزمایشی که تعداد آزمایش دوتا بیشتر از نمودار درختی می‌توان کمک گرفت.

مثال ۷: سکه‌ای را سه بار پرتاب می‌کنیم فضای نمونه آن را بنویسید.

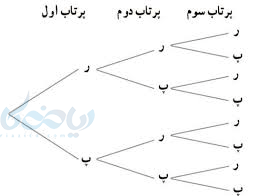
به هر یک از زیرمجموعه‌های فضای نمونه یک پیشامد تصادفی می‌گویند.

با توجه به اینکه تعداد زیرمجموعه‌ها یک مجموعه \( \Large n \) عضوی \( \Large 2^n \) است. پس هر فضای نمونه \( \Large n \) عضوی \( \Large 2^n \) پیشامد تصادفی خواهد داشت که آن‌ها را با حروف \( \Large A,B,….. \)

مثال ۸: در آزمایش پرتاب یک سکه تمام پیشامد‌های تصادفی ممکن را بنویسید.

مثال ۹: دو تاس را با هم پرتاب می‌کنیم. مطلوبست:

الف) تعداد فضای‌ نمونه

ب) پیشامد آن‌ها هر دو عدد زوج بیابند.

پ) پیشامد آنکه مجموع عددهای آمده برابر 10 باشد.

ت) اولی زوج و دومی مضرب 5 باشد.

(برای جواب این سوال از جدول می‌توان کمک گرفت)

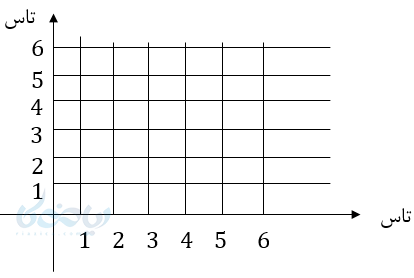
الف)

\( \LARGE n(S)=36 \)

ب)

پ)

\( \LARGE B=\{(4,6),(5,5),(6,4)\} \)

\( \LARGE n(B)=3 \)

ت)

\( \LARGE C=\{(2,5),(4,5),(6,5)\} \)

\( \LARGE n(C)=3 \)

مثال ۱۰: خانواده‌ای با 3 فرزند داریم که از جنسیت آن‌ها اطلاع نداریم. اگر ترتیب به دنیا آمدن فرزندان اهمیت داشته باشد. مطلوبست:

الف) فضای نمونه آزمایش.

ب) پیشامد آنکه تعداد فرزندان پسر بیشتر از دختر باشد.

پ) هر سه فرزند هم‌جنس باشند.

ت) دقیقا یک دختر در خانواده بدنیا آمده باشد.

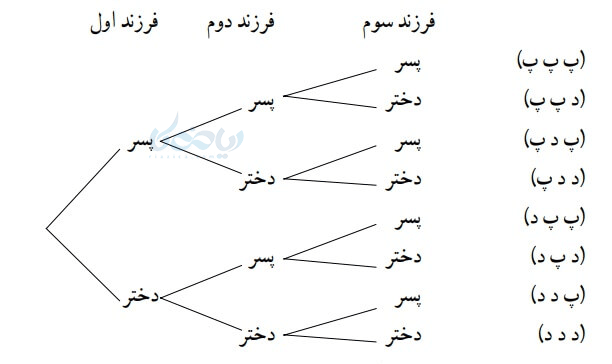
الف)

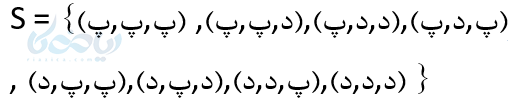
ب)

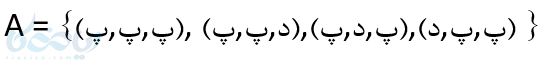
پ)

ت)

پیشامد و برخی اعمال روی آن‌ها در آموزش احتمال

اگر \( \Large A,B \) پیشامدهایی در فضای نمونه باشند. داریم:

الف) اجتماع دو پیشامد

پیشامد \( \Large (A\cup B) \) وقتی رخ می‌دهد (اتفاق می‌افتد) که حداقل یکی از دو پیشامد \( \Large A \) یا \( \Large B \) یا هر دو رخ دهند.

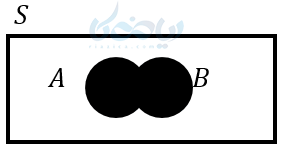
ب) اشتراک دو پیشامد

پیشامد \( \Large (A \cap B) \) وقتی رخ می‌دهد (اتفاق می‌افتد) که هم پیشامد \( \Large A \) و هم پیشامد \( \Large B \) رخ دهند.

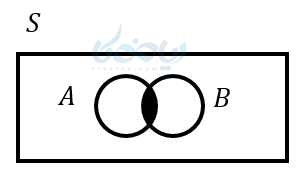
ب) تفاضل دو پیشامد

پیشامد \( \Large (A – B) \) وقتی رخ می‌دهد (اتفاق می‌افتد) که پیشامد \( \Large A \) رخ دهد ولی پیشامد \( \Large B \) رخ ندهد.

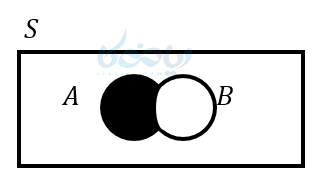
مثال ۱۱: دو تاس را با هم پرتاب می‌کنیم. اگر داشته باشیم:

پیشامد آنکه هر دو تاس زوج باشند \( \LARGE A \)

پیشامد آنکه مجموع دو تاس ده باشد \( \LARGE B \)

پیشامد آنکه تاس اول فرد باشد \( \LARGE C \)

الف) اعضای هر کدام از پیشامدها را بنویسید.

ب) پیشامد آنکه هر دو تاس زوج و مجموع آن‌ها ده باشد را بنویسید.

پ) پیشامد آنکه هر دو تاس زوج یا مجموع آن‌ها ده باشد را بنویسید.

ت) پیشامد آنکه هر دو تاس زوج باشند ولی مجموع آن‌ها ده نشود.

ث) پیشامد آنکه عدد اول فرد بیابید ولی مجموع آن‌ها ده نشود.

الف)

ب)

پ)

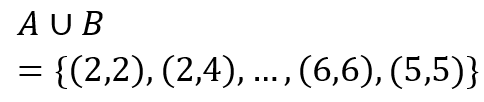
ت)

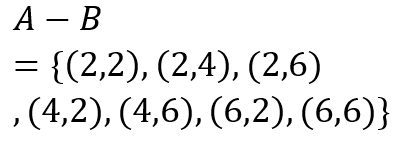
ث)

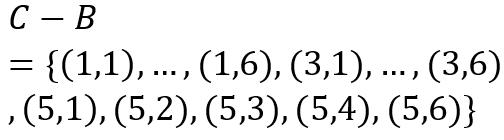
متمم یک پیشامد در آموزش احتمال دهم

اگر \( \Large A \) یک پیشامد از فضای نمونه \( \Large S \) باشد، متمم پیشامد \( \Large A \) وقتی رخ می‌دهد که \( \Large A \) رخ ندهد. در این حالت آن را با \( \Large A’ \) و یا \( \Large A^C \) نمایش می‌دهند. داریم:

\( \LARGE A \cup A’=S \)

\( \LARGE A \cap A’=\emptyset \)

مثال ۱۲ از احتمال دهم: اگر در پرتاب یک تاس \( \Large A \) پیشامد عدد بزرگتر از 2 آمدن باشد، متمم آن را بنویسید.

\( \LARGE  A’=\{3,4,5,6\} \)

\( \LARGE  A=\{1,2\} \)

مثال ۱۳: یک تاس و یک سکه را پرتاب کرده‌ایم اگر \( \Large A \) پیشامد سکه رو آمدن و تاس عدد زوج باشد. متمم آن را بنویسید.

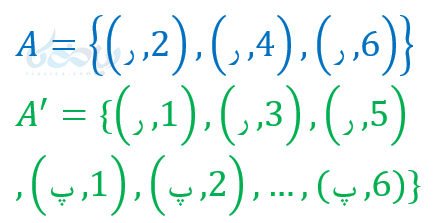
دو پیشامد ناسازگار

اگر \( \Large A,B \) دو پیشامد از فضای نمونه \( \Large S \) باشند بطوریکه \( \Large A \cap A’=\emptyset \) در این صورت \( \Large A,B \) را دو پیشامد ناسازگار می‌گویند. دو پیشامد ناسازگار هیچ‌گاه با هم رخ نمی‌دهند.

نکته ۵: دو پیشامد متمم حتما ناسازگارند ولی عکس این مطلب درست نیست.

مثال ۱۴: اگر در پرتاب یک تاس \( \Large A \) پیشامد عدد بزرگتر از 4 باشد و \( \Large B \) پیشامد عدد کوچکتر از 3 آمدن باشد، آیا این دو پیشامد ناسازگارند؟ آیا متمم یکدیگر هستند؟

\( \LARGE S=\{1,2,…,6\} \)

\( \LARGE A=\{5,6\} \)

\( \LARGE B=\{1,2\} \)

\( \LARGE \begin{cases} A \cap A’=\emptyset \\A \cup A’ \neq S \end{cases} \)

ناسازگارند ولی متمم نیستند.

---

---

احتمال رخداد یک پیشامد (اندازه گیری شانس)

اگر \( \Large A \) یک پیشامد از فضای نمونه \( \Large S \) باشد، \( \Large (A \subseteq S) \) احتمال رخداد \( \Large A \) را که با \( \Large P(A) \) نمایش می‌دهند. برابر است با:

\( \LARGE P(A)=\frac{n(A)}{n(S)} \)

که عدد حقیقی بین صفر و یک است:

\( \LARGE 0  \leq P(A) \leq 1 \)

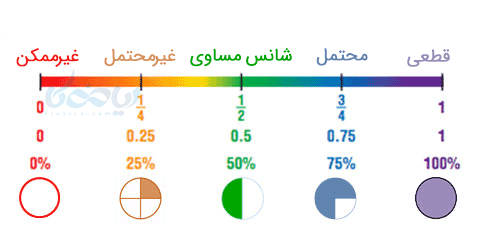
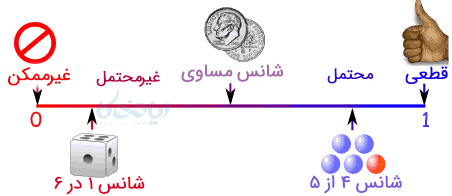
که هر چه \( \Large P(A) \) به صفر نزدیک باشد شانس رخداد \( \Large A \) کمتر (غیرمحتمل) و هرچه به یک نزدیک باشد شانس رخداد \( \Large A \) بیشتر (محتمل) است.

پیشامد حتمی

اگر \( \Large P(A) =1 \) باشد، می‌گوییم احتمال رخداد پیشامد \( \Large A \) حتمی (قطعی) است.

پیشامد غیر ممکن

اگر  \( \Large P(A) =0 \) باشد، می‌گوییم احتمال (شانس) رخداد پیشامد \( \Large A \) غیرممکن است.

نکته ۶: در مسائل این بخش دقت کنید گاهی خود فضای نمونه را می‌خواهد گاهی تعداد فضای نمونه و در مورد پیشامدها هم گاهی خود پیشامد را می‌خواهد گاهی تعداد آن‌ها و گاهی احتمال وقوع آن پیشامد را برای همین باید به صورت مسئله دقت کنید که دچار اشتباه نشوید.

مثال ۱۵: در پرتاب دو تاس مطلبوست احتمال اینکه:

الف) هر دو تاس زوج بیابید.

ب) مجموع دو عدد آمده بیشتر از نه باشد.

پ) اولی زوج و دومی فرد باشد.

فضای نمونه این مسئله  \( \Large n(S) =36 \)  است. در قسمت الف اگر پیشامد هر دو زوج آمدن را \( \Large A \)  بگیریم. \( \Large A \) عبارت است از:

\( \LARGE A \)

\( \Large =\{(2,2),(2,4),..,(6,6)\} \)

\( \LARGE n(A)=9 \)

اما در این مسئله \( \Large P(A) \) یعنی احتمال وقوع \( \Large A \) را خواسته. پس داریم:

\( \LARGE P(A)=\frac{n(A)}{n(S)}=\frac{9}{36}=\frac{1}{4} \)

ب) اگر پیشامد مجموع دو عدد آمده بیشتر از نه باشد را \( \Large B \) بگیریم. داریم:

\( \LARGE B=\{(4,6),(5,5),(5,6) \)

\( \LARGE ,(6,4),(6,5),(6,6)\} \)

\( \LARGE n(B)=6 \)

\( \LARGE P(B)=\frac{n(B)}{n(S)}=\frac{6}{36}=\frac{1}{6} \)

پ) اگر پیشامد اولی زوج و دومی فرد را \( \Large C \) بگیریم. داریم:

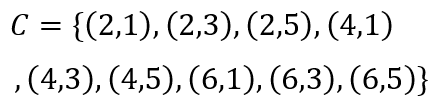
\( \LARGE n(C)=9 \)

\( \LARGE P(C)=\frac{n(C)}{n(S)}=\frac{9}{36}=\frac{1}{4} \)

دقت کنید در این مسئله نوشتن خودپیشامد‌های \( \Large A,B,C \) لازم نیست اما ما برای فهم بهتردر مثال بالا آن‌ها را نوشتیم و آنچه مهم است \( \Large P(A),P(B),P(C) \)

مثال ۱۶: از احتمال دهم: درجعبه‌ای 8 لامپ وجود دارد که 4 لامپ معیوب است اگر به تصادف 3 لامپ از جعبه خارج کنید. مطلوبست احتمال آنکه:

الف) هر سه لامپ معیوب باشد.

ب) دو لامپ سالم و یکی معیوب باشد.

ج) حداقل یکی سالم باشد.

در این مسئله چون احتمال وقوع این پیشامدها را خواسته پس به \( \Large n(S) \) نیاز داریم که انتخاب 3 لامپ از بین 8 لامپ می‌باشد.

\( \LARGE n(S)=\begin{pmatrix} 9\\ 3 \end{pmatrix} \)

\( \LARGE =\frac{9!}{3! \times 6!}=\frac{9 \times 8 \times 7 \times 6!}{6 \times 6!}=84 \)

الف)

\( \LARGE P(A)=\frac{n(A)}{n(S)}=\frac{\begin{pmatrix} 4\\ 3 \end{pmatrix}}{\begin{pmatrix} 9\\ 3 \end{pmatrix}} \)

\( \LARGE =\frac{4}{84}=\frac{1}{21} \)

ب)

\( \LARGE P(B)=\frac{n(B)}{n(S)} \)

\( \LARGE \frac{\begin{pmatrix} 5\\ 2 \end{pmatrix} \times \begin{pmatrix} 4\\ 1 \end{pmatrix}}{\begin{pmatrix} 9\\ 3 \end{pmatrix}} \)

\( \LARGE =\frac{10 \times 4}{84}=\frac{10}{21} \)

ج)

 

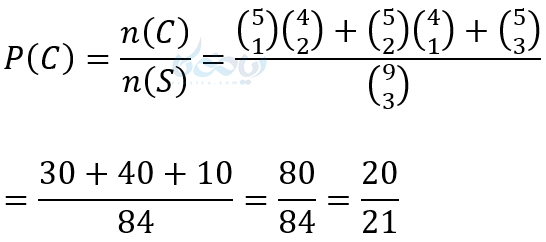
نکته ۷ از احتمال دهم: در مسئله بالا احتمال رخ داد قسمت ج از همه بیشتر و قسمت الف از همه کمتر است.

مثال ۱۷: فرض کنید با اعداد 2 و 3 و 4 و 8 اعداد سه رقمی بدون تکرار می‌نویسیم و آن اعداد را روی کارت‌هایی می‌نویسیم و یک کارت به تصادف انتخاب می‌کنیم. مطلوبست احتمال آنکه:

الف) عدد آمده زوج باشد.

ب) عدد آمده بزرگتر از چهارصد باشد.

باز در این مسئله احتمال را می‌خواهیم پس \( \Large n(S) \) را باید محاسبه کنیم با توجه به اصل ضرب داریم:

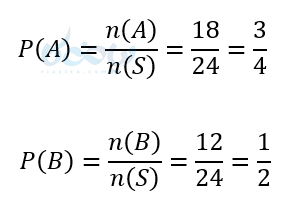
چون \( \Large P(A)>P(B) \) پس احتمال وقوع قسمت الف بیشتر است.

مثال ۱۸: ثابت کنید: \( \Large 0 \leq P(A) \leq 1 \)

می‌دانیم

\( \LARGE A \subseteq S \)

\( \LARGE \rightarrow 0 \leq n(A) \leq n(S) \)

طرفین را به \( \Large n(S) \) تقسیم می‌کنیم.

\( \LARGE \frac{0}{n(S)} \leq \frac{n(A)}{n(S)} \leq \frac{n(S)}{n(S)} \)

\( \LARGE \rightarrow  0 \leq P(A) \leq 1 \)

مثال ۱۹: ثابت کنید: \( \Large P(S)=1 , P(\emptyset)=0 \)

\( \LARGE P(S)=\frac{n(S)}{n(S)} =1\)

\( \LARGE P(\emptyset)=\frac{n(\emptyset)}{n(S)} = \frac{0}{n(S)}  =0\)

مثال ۲۰: رابطه زیر را ثابت کنید:

\( \Large P(A \cup B) \)

\( \Large =P(A)+P(B)-P(A \cap B) \)

می‌دانیم

\( \Large n(A \cup B) \)

\( \Large =n(A)+n(B)-n(A \cap B) \)

طرفین را به  \( \Large n(S) \)  تقسیم می‌کنیم.

\( \LARGE \frac{n(A \cup B)}{n(S)} \)

\( \LARGE =\frac{n(A )}{n(S)}+\frac{n(B)}{n(S)}-\frac{n(A \cap B)}{n(S)} \)

\( \Large \rightarrow P(A \cup B) \)

\( \Large = P(A)+P(B)-P(A \cap B) \)

نکته ۸: اگر \( \Large A,B \) ناسازگار باشند. داریم:

\( \Large  P(A \cup B) \)

\( \Large = P(A)+P(B) \)

مثال ۲۱: اگر \( \Large A’ \) متمم پیشامد \( \Large A \) در فضای نمونه \( \Large S \) باشد. ثابت کنید: \( \Large P(A )=1-p(A’) \)

می‌دانیم

\( \LARGE A \cup A’ = S  \)

\( \LARGE \rightarrow P(A \cup A’) = P(S) \)

از طرفی می‌دانیم

\( \Large P(A \cup B) \)

\( \Large =P(A)+P(B)-P(A \cap B) \)

\( \LARGE P(S) \)

\( \LARGE =P(A)+P(A’)-P(\emptyset) \)

از طرفی می‌دانیم

\( \Large P(S)=1 , P(\emptyset)=0 \)

پس می‌شود:

\( \LARGE P(A)+P(A’)=1 \)

\( \LARGE \rightarrow \begin{cases} P(A)=1-P(A’) \\ P(A’)=1-P(A) \end{cases} \)

از این مطلب در مواردی که محاسبه متمم یک پیشامد از محاسبه خود پیشامد ساده‌تر است باشد استفاده می‌شود.

مثال ۲۲ از احتمال دهم: در پرتاب دو تاس مطلوبست احتمال آنکه مجموع اعداد به دست آمده ده نباشد را محاسبه کنید.

در این مثال راحتر است که ابتدا احتمال متممش را خساب کنیم بعد احتمال خواسته شده را

متمم این پیشامد می‌شود مجموعه اعداد آمده ده باشد.

\( \LARGE P(A’)=\frac{n(A’)}{n(S)} \)

\( \LARGE  =\frac{3}{36}=\frac{1}{12}\)

\( \LARGE P(A)=1-P(A’)  \)

\( \LARGE  = 1-\frac{1}{12}=\frac{11}{12} \)

مثال ۲۳: اگر دو تاس را با هم بیندازیم چقدر احتمال دارد که:

الف) مجموع دو تاس 8 یا هر دو تاس فرد باشند.

ب) مجموع دو تاس 9 یا هر دو زوج باشند.

الف)

\( \Large A \) مجموع دو تاس 8

‌

\( \Large B \) هر دو تاس فرد

\( \LARGE P(A)=\frac{n(A)}{n(S)} =\frac{5}{36}\)

\( \LARGE P(B)=\frac{n(B)}{n(S)} =\frac{9}{36}\)

\( \LARGE P(A \cap B) =\frac{2}{36}\)

\( \Large P(A \cup B) \)

\( \Large =P(A)+P(B)-P(A \cap B) \)

\( \Large P(A \cup B)=\frac{5}{36} + \frac{9}{36} – \frac{2}{36} \)

\( \LARGE P(A \cup B)= \frac{12}{36}= \frac{1}{3} \)

ب)

\( \Large A \) مجموع دو تاس 9

‌

\( \Large B \) هر دو تاس زوج

‌

\( \Large A,B \) با هم ناسازگارند زیر مجموع دو عدد زوج، زوج می‌شود.

‌

\( \LARGE P(A)=\frac{n(A)}{n(S)} =\frac{4}{36}\)

\( \LARGE P(B)=\frac{n(B)}{n(S)} =\frac{9}{36}\)

\( \Large P(A \cup B) \)

\( \Large =P(A)+P(B) \)

\( \LARGE =\frac{4}{36}+\frac{9}{36}=\frac{13}{36} \)

توصیه میشه قبل از خوندن این پست ،پست آموزش احتمال هشتم رو مطالعه کنید.

---

---

زنگ آخر آموزش احتمال دهم

در این نوشتار از مجموعه‌ آموزش ریاضی دهم، به کامل‌ترین و جامع‌ترین شکل ممکن باهم آموزش احتمال دهم را یادگرفتیم. در این آموزش ابتدا اصطلاحات مختلفی که در احتمال کاربرد دارد را یاد گرفتیم. بیش از ۲۰ مثال متنوع باهم حل کردیم و همچنین اشکال مختلفی را که در جهت فهم بیشتر این آموزش بود دیدیم.

درصورتیکه هرگونه سوالی از آموزش احتمال دهم دارید، می‌توانید سوال خود را در بخش دیدگاه‌ها در پایین همین نوشتار برای ما بگذارید. کارشناسان ریاضیکا در کوتاه‌ترین زمان به شما پاسخ خواهند داد.

به خوندن ادامه بده!

آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!