آموزش ریاضی پایه دهم
روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
در بین نسبت های مثلثاتی روابط زیبایی وجود دارد که میتوان با داشتن یک نسبت و این روابط، بقیه نسبتها را نیز بدست آورد. این روابط یا همان اتحادهای مثلثاتی کاربردهای زیادی در ساده کردن روابط و حل معادلات مثلثاتی دارند.
در ادامه به شرح ۸ تا از مهمترین روابط مثلثاتی که در کتاب ریاضی پایه دهم آمدهاند میپردازیم.
اثبات ۸ رابطه مثلثاتی دهم در چهار دسته بندی
دسته اول روابط مثلثاتی:
مثلث ABC را در نظر بگیرید. در این مثلث نسبت های مثلثاتی زیر برقرار هستند:
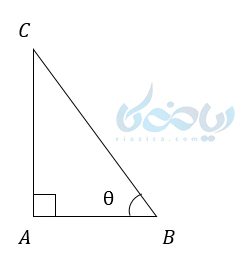
\( \LARGE sin \theta = \frac{AC}{BC} \)
\( \LARGE cos \theta = \frac{AB}{BC} \)
\( \LARGE tan \theta = \frac{AC}{AB} \)
\( \LARGE cot \theta = \frac{AB}{AC} \)
حال اگر سینوس را بر کسینوس تقسیم کنیم خواهیم داشت :
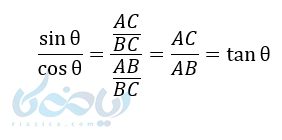
و اگر کسینوس را بر سینوس تقسیم کنیم داریم :
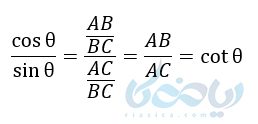
پس از دو رابطه بالا میتوانیم روابط زیر را نتیجه بگیریم :
\( \LARGE tan \theta = \frac{sin \theta}{cos \theta} \)
\( \LARGE cot \theta = \frac{cos \theta}{sin \theta} \)
نکته ۱روابط مثلثاتی: از روی دایره مثلثاتی هم میتوان این روابط مثلثاتی را اثبات نمود.
نکته ۲ روابط مثلثاتی: چون
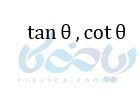
معکوس هم هستند، پس داریم :

دسته دوم روابط مثلثاتی:
در مثلث ABC طبق قضیه فیثاغورس داریم :
\( \LARGE AB^2 + AC^2 = BC^2 (1) \)
از طرفی داریم
\( \LARGE sin^2 \theta + cos^2 \theta \)
\( \LARGE = \frac{AC^2}{BC^2} + \frac{AC^2+AB^2}{BC^2} (1) \)
\( \LARGE = \frac{BC^2}{BC^2} = 1 \)
پس برای هر زاویه دلخواه \( \Large \theta \) داریم :
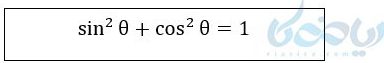
دسته سوم – رابطه طلایی در روابط مثلثاتی :
از رابطه بالا دو رابطه مهم نتیجه میگیریم که به روابط طلایی معروف هستند:

دسته چهارم روابط مثلثاتی:
حال میخواهیم رابطه بین \( \Large tan \theta \) و \( \Large cos \theta \) را پیدا کنیم تا با داشتن یکی به راحتی دیگری را نیز بدست آورید:
\( \LARGE 1 + tan^2 \theta \)
\( \LARGE = 1 + \frac{sin^2 \theta}{cos^2 \theta} \)
\( \LARGE = \frac{sin^2 \theta + cos^2 \theta}{cos^2 \theta} \)
\( \LARGE = \frac{1}{cos^2 \theta} \)
پس در نهایت میتوان رابطه زیر را نتیجه گرفت:
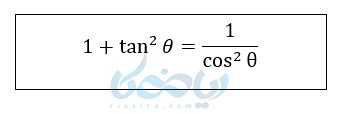
به همین ترتیب میتوانیم رابطه بین \( \Large cot \theta \) و \( \Large sin \theta \) را پیدا کنیم.
\( \LARGE 1 +cot^2 \theta \)
\( \LARGE = 1 + \frac{cos^2 \theta}{sin^2 \theta} \)
\( \LARGE = \frac{sin^2 \theta + cos^2 \theta}{sin^2 \theta} \)
\( \LARGE = \frac{1}{sin^2 \theta} \)
پس رابطهی بین این دو نیز برابر است با:
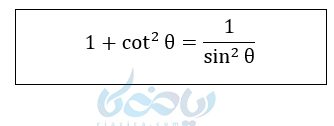
در اینجا میتوانید جمعبندی تمامی دستههای روابط بین نسبت های مثلثاتی را به صورت یکجا مشاهده کنید:
(1
\( \LARGE cos^2 \theta + sin^2 \theta = 1 \)
(2
\( \LARGE sin^2 \theta = 1 – cos^2 \theta \)
(3
\( \LARGE cos^2 \theta = 1 – sin^2 \theta \)
(4
\( \LARGE tan \theta = \frac{sin \theta}{cos \theta} \)
(5
\( \LARGE cot \theta = \frac{cos \theta}{sin \theta} \)
(6
\( \LARGE tan \theta \times cot \theta = 1 \)
(7
\( \LARGE 1 + tan^2 \theta = \frac{1}{cos^2 \theta} \)
(8
\( \LARGE 1 + cot^2 \theta = \frac{1}{sin^2 \theta} \)
این 8 رابطه مهمترین روابط مثلثاتی بین نسبتها هستند. البته روابط زیادی بین نسبتها وجود دارد که برای اثبات آنها باید از این 8 رابطه استفاده کنید.
اثبات اتحادهای مثلثاتی با استفاده از روابط بین نسبت های مثلثاتی
برای اثبات اتحادهای مثلثاتی باید از یک طرف به طرف دیگر برسیم که البته فرقی نمیکند از کدام سمت معادله شروع کنیم. اما نکتهای که باید به آن توجه داشته باشید این است که از کدام طرف رابطه میتوانید اثبات را شروع کنید. در ادامه با اَعمال ریاضی و حتی گاهی با اضافه و کم کردن و یا ضرب صورت و مخرج در یک مقدار، باید به طرف دیگر برسید.
اثبات یکی از روابط با استفاده ازدسته دوم روابط مثلثاتی
مثال ۱:اتخاد مثلثاتی زیر را اثبات کنید.
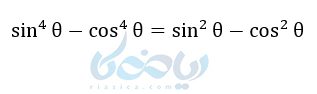
اگر کمی دقت کنید با توجه به توان بزرگتر طرف اول (سمت چپ) بهتر است از طرف اول به دوم برسیم، در این جا از تجزیه اتحاد مزدوج استفاده میکنیم :
\( \LARGE sin^4 \theta – cos^4 \theta \)
\( \LARGE = (sin^2 \theta – cos^2 \theta) \)
\( \LARGE \times (sin^2 \theta + cos^2 \theta) \)
\( \LARGE= sin^2 \theta – cos^2 \theta \)
به همین راحتی به طرف دوم رسیدیم. اگر این عملیات را برعکس انجام دهیم به طرف اول خواهیم رسید:
\( \LARGE sin^2 \theta – cos^2 \theta \)
\( \LARGE = (sin^2 \theta – cos^2 \theta) \times 1 \)
\( \LARGE = (sin^2 \theta – cos^2 \theta) \)
\( \LARGE \times (sin^2 \theta + cos^2 \theta) \)
\( \LARGE = sin^4 \theta – cos^4 \theta \)
اثبات یکی دیگر از اتحادهای مثلثاتی
مثال ۲:اتحاد مثلثاتی زیر را اثبات کنید.

در این مثال میبینید از هیچ یک از روابطی که خواندیم نمیتوانیم استفاده کنیم. پس کافیست صورت و مخرج را در \( \Large ۱- sin \theta \) که مزدوج \( \Large ۱+ sin \theta \) است ضرب کنیم :
طرف اول
\( \LARGE \frac{cos \theta}{ 1 + sin \theta} \times \frac{ 1 – sin \theta}{ 1 – sin \theta} \)
\( \LARGE = \frac{cos \theta (1 – sin \theta) }{ 1 – sin^2 \theta} \)
\( \LARGE = \frac{cos \theta (1 – sin \theta) }{ cos^2 \theta} \)
\( \LARGE = \frac{1 – sin \theta }{ cos \theta} \)
رسیدیم به طرف دوم
حال اگر بخواهیم از طرف دوم به اول برسیم، میتوانیم صورت و مخرج را در \( \Large cos \theta \) یا \( \Large ۱+ sin \theta \) ضرب کنیم. اینها ترفندهایی است که ما در ریاضیات برای اثبات یک تساوی استفاده میکنیم:
طرف دوم
\( \LARGE \frac{1 – sin \theta}{ cos \theta} \times \frac{ cos \theta}{cos \theta} \)
\( \LARGE = \frac{cos \theta (1 – sin \theta) }{ cos^2 \theta} \)
\( \LARGE = \frac{cos \theta (1 – sin \theta) }{ 1 – sin^2 \theta} \)
\( \LARGE = \frac{cos \theta (1 – sin \theta) }{ (1 – sin \theta)(1 + sin \theta)} \)
\( \LARGE = \frac{cos \theta }{ 1 + sin \theta} \)
رسیدیم به طرف اول
حال شما صورت و مخرج را در \( \Large ۱+ sin \theta \) ضرب کرده و از طرف دوم به اول برسید.
کاربرد دیگر روابط مثلثاتی وقتی است که، یک نسبت را داریم و میخواهیم نسبت دیگری را بدست آوریم. به مثال زیر دقت کنید.
مثال۳: نسبت های مثلثاتی : \( \Large tan \theta = 2 \) و \( \Large \theta \) در ربع سوم میباشد سایر نسبت های مثلثاتی را بدست آورید ؟
جواب :
\( \LARGE tan \theta = 2 \Rightarrow cot \theta = \frac{1}{2} \)
\( \LARGE tan \theta = 2 \)
\( \LARGE 1 + tan^2 \theta = \frac{1}{cos^2 \theta} \)
\( \LARGE 1 + 4 = \frac{1}{cos^2 \theta} \)
\( \LARGE cos^2 \theta = \frac{1}{5} \)
\( \LARGE cos \theta = – \frac{\sqrt5}{5} \)
علامت کسینوس منفی است، چون در ربع سوم است.
\( \LARGE sin^2 \theta = 1 – cos^2 \theta \)
\( \LARGE sin^2 \theta = 1 – \frac{5}{25} \)
\( \LARGE sin^2 \theta = \frac{20}{25} \)
\( \LARGE sin \theta = – \frac{2\sqrt5}{5} \)
علامت سینوس منفی است، چون در ربع سوم است.
برای آموزش مطالب بیشتر در مورد مثلثات به پستهای دایره مثلثاتی و محاسبه مساحت مثلث بدون داشتن ارتفاع و آموزش نسبت های مثلثاتی مراجع کنید
ویدیو از روابط بین نسبت های مثلثاتی
در این ویدیو یک نمونه سوال از اتحاد های مثلثاتی که به کمک روابط بین نسبت های مثلثاتی حل شده است برای شما آورده شده است.
کلام آخر روابط بین نسبت های مثلثاتی
شما دانشآموزان عزیز با استفاده از مثالهایی که در این پست آموزشی از وبسایت ریاضیکا دیدید، میتوانید روابط بیشتری را با کمک اتحادها اثبات کنید. با انجام اینکار خواهید فهمید که این کار تا چه حد لذت بخش بوده و چقدر راحت میتوان یک اتحاد مثلثاتی را اثبات کرد. اینکار همچنین به فهم بیشتر شما از ریاضیات کمک خواهد کرد.
در صورتیکه هر سوالی از این بخش داشتید میتوانید در بخش نظرات سوال خود را مطرح کرده و کارشناسان ریاضی ما به سرعت پاسخ شما را خواهند داد.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!





واقعا عالی بود ? 🙂
خوشحالیم که براتون مفید بوده
موفق و پیروز باشید
عبارت های زیر را ثابت کنید
(1+سینوس تتا) (۱ _سینوس تتا)=کسینوس به توان دو تتا
سلام و وقت به خیر پست روابط مثلثاتی را کامل بخونید متوجه می شوید.
سلام اگه تو طرف اول دو تا کسر بود و با هیچ فرمولی نشه حل کرد اون موقع چی؟
سلام دوست عزیز
حتما راه حلی برای آن است و باید خوب بهش دقت کنید و حواستون به طرف دوم هم باشد.
خیلی خوب بود ممنون
با عرض سلام خوشحالیم که براتون مفید بوده
بسیار عالی من این نکات رو تو کلاس کنکور های سطح بالا خوندم ❤️??
با سلام وادب
هدف ما اینه جامع و کامل وساده مطالب رو بیان کنیم
ببخشیدا شما…
اینا دقیقا در کتاب دهم هست😏
سلام مگه قرار بود نباشه
سلام خسته نباشید. مطالب مفیدی بود. اما من گاهی گیر میکنم تو حل سوالات و هر کاری می کنم به طرف دوم نمیرسم?
سلام و عرض ادب
ممنون از انرژی که دادید.
گاهی باید از طرف دوم به اول برسید، با شگردهای ریاضی مثل ضرب صورت و مخرج در یک عبارت و اضافه و کم کردن مقداری برای کمک و مسلط به ۸ رابطه آمده در پست و اتحاد و تجزیه و نمونه سوال حل کردن زیاد به تبحر برسید.
موفق باشید.
با عرض سلام و خسته نباشید خدمت ادمین،مطالب مفیدی بودن،خدا قوت
انشالله همیشه اینطوری موفق و مفید پیش برید
با سلام وعرض ادب
خوشحالیم که برای شما مفید واقع شده وممنون از دعای خیر شما
واقعا اطلاعات مفیدی بود خیلی ممنونم , حتما به دوستانم هم میگم که مشاهده کنن ,سپاس از لطفتون?
سلام و عرض ادب
ممنون از توجهی که به ما داشتید.
موفق باشید.
از سمت چپ یه اتحاد مزدوج میگیریم تا به عبارت ( ۱- سینوس به توان دو تتا) برسیم. این عبارت با کسینوس به توان دو تتا برابره
توی پست هم هست
خیلی عالی بود . دستتون درد نکنه
سلام و عرض ادب
ممنون از توجهاتتون
موفق باشید
خیلی عالی و پر محتوا بود…لطفا بیشتر نمونه سوال و برای ما حلش رو بزارید
با سلام واحترام
انشالله در آینده نزدیک نمونه سوال خواهیم گذاشت
خیلی عالی بود،
موقع مطالعه جزوات این فصل حس میکنم یه جور بازی رو دارم اموزش میبینم،واقعا دمتون گرم?
با سلام وعرض ادب
هدف ما هم همینه دوست عزیز با تهیه پکیج ویدیی ما لذت یادگیریتون رو بیشتر کنید
سلام خسته نباشید
تو محاسبه مساحت یک مثلث ۹۰ درجه اضلاعی که در هم ضرب می شوند باید اون هر دو ضلع مربوط به اضلاع قاعمه باشن یا میشه یکی از اضلاع وتر باشه؟
باسلام وادب
فرقی نداره کدوم ضلع فقط در سینوس زاویه بینشون باید ضرب بشه
?️?? خیلی خوب بود مرسیییی
خیلی کامل تر و واضح تر از توضیحات دبیرمون تو کلاس بود??
با سلام وادب
ممنون از نظر لطف شما
خیلی خوب بود خیلی کامل بود?
با سلام دوست عزیز
ممنون از نظر لطف شما