آموزش ریاضی پایه دهم
آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
ما در درسنامه نابرابری ونامعادله ریاضی نهم حل نامعادله درجه اول را فراگرفتیم و در درسنامه تعیین علامت عبارت های جبری به زبان ساده تعیین علامت عبارتهای جبری وگویا وغیره را آموختیم. حال در این درسنامه به حل دستگاه نامعادلات ونامعادلات درجه دوم وگویا و نامعادله قدر مطلقی می پردازیم در این بخش به شما آموزش حل نامعادله را به زبان ساده و شیوا یاد میدهیم.
تعریف نامعادله
اگر \( \Large A , B \) دو عبارت جبری باشند، نامعادلههایی که از این دو عبارت ساخته میشوند به صورت زیر میباشند:
| میخوانیم | نامعادله |
|---|---|
| A کوچکتر از B | \( \LARGE A < B \) |
| A کوچکتر یا مساوی B | \( \LARGE A \leq B \) |
| A بزرگتر از B | \( \LARGE A > B \) |
| A بزرگتر یا مساوی B | \( \LARGE A \geq B \) |
برای حل یک نامعادله میتوانیم مانند معادله به دو طرف آن عدد یا عبارت مثبت یا منفی اضافه کنیم. (خاصیت جمع)
یعنی:
\( \LARGE A < B \)
\( \LARGE \rightarrow A+C<B+C \)
حال بیایید در مورد ضرب دو طرف نامعادله در یک عدد یا عبارت گفتگو کنیم. اگر آن عدد و با عبارت مثبت باشد، جهت نامعادله عوض نمیشود. اما اگر منفی باشد، جهت نامعادله عوض میشود. (خاصیت ضرب)
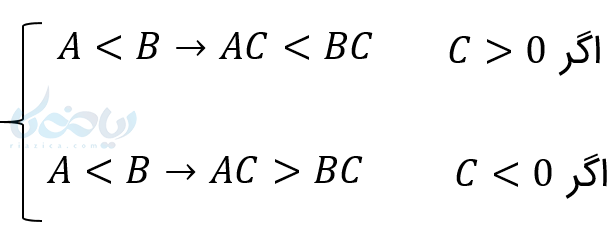
در آموزش حل نامعادله با این خاصیتها نامعادلات ساده درجه اول به راحتی قابل حل هستند.
مثال۱: نامعادله \( \LARGE 6x-2 \geq 4x-8 \) را حل کنید؟
حل ۱:
\( \LARGE 6x-2 \geq 4x-8 \)
در واقع دو طرف را با \( \Large +2 , -4x \) جمع میکنیم.
\( \LARGE 6x-4x \geq 2-8 \)
\( \LARGE 2x \geq -6 \)
\( \LARGE x \geq -3 \)
بنابر این جواب نامعادله تمام اعداد حقیقی بزرگتر و مساوی 3- میباشد. درنهایت میتوانیم مجموعه جواب را به زبان ریاضی یا به صورت بازه بنویسیم:
\( \LARGE \{x|x\in \mathbb{R},x\geq-3\} \) = مجموعه چواب
\( \LARGE =[-3,+\infty) \)
آموزش حل نامعادله: نامعادلات دوگانه یا دستگاه نامعادلات
اگر عبارتی همزمان در دو نامعادله به صورت زیر صدق کند:
\( \LARGE \begin{cases} A < B \\ C < A \end{cases} \)
\( \LARGE \rightarrow C<A<B \)
برای حل نامعادلات دوگانه میتوان هر نامعادله را جداگانه حل کرد، سپس بین جوابها اشتراک گرفت. اما اگر \( \Large B , C \) عدد باشند میتوان آنها را به همان صورت \( \Large C<A<B \) با هم حل کرد.
مثال۲: دستگاه نامعادلات زیر را حل کنید.
حل ۲:
\( \LARGE \begin{cases} 4x-2>-3 \\ 4x-2 \leq 9 \end{cases} \)

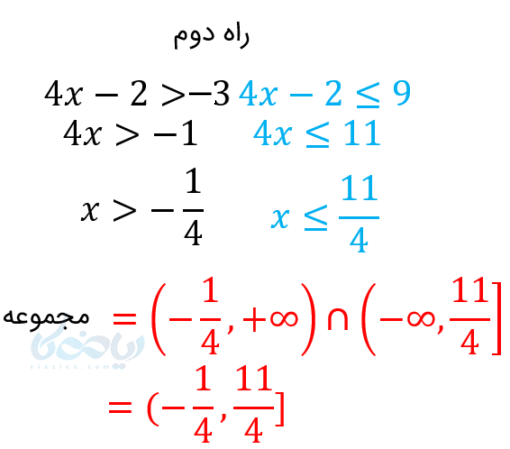
مثال۳: نامعادله \( \LARGE x+1 \leq 5-x < 2x+3 \) را حل کنید.
حل ۳:
این مثال نیز در واقع یک نامعادله دوگانه است ولی باید حتما آن را جداگانه حل کرد و بعد بین جوابها اشتراک گرفت.
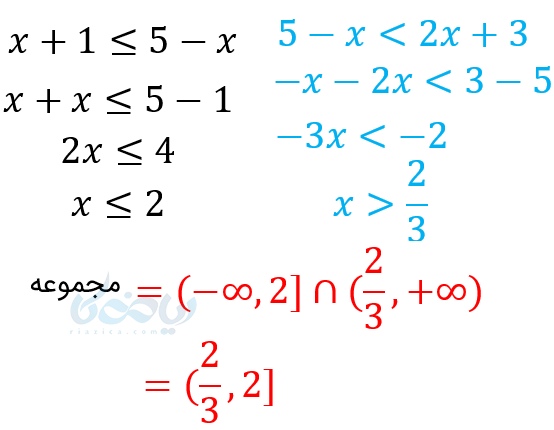
اگر نتوانستید ذهنی اشتراک بگیرید کافیست روی محور آنها رسم و قسمت مشترک پیدا کنید.
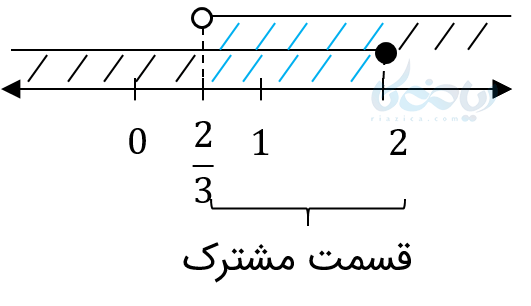
نکته آموزش حل نامعادله : گاهی هیچ قسمت مشترکی ندارند و مجموعه جواب تهی خواهد بود.
آموزش حل نامعادله: نامعادله درجه دوم و نامعادله گویا
در آموزش ریاضی دهم یاد میگیریم، برای حل نامعادلات درجه دوم و گویا باید حتما از تعیین علامت استفاده کنیم. برای اینکار ابتدا تمام عبارات را به یک طرف برده و یک طرف نامعادله را صفر میکنیم. یعنی به صورت \( \Large A>0 \) یا \( \Large A<0 \) در میآوریم سپس عبارت \( \Large A \) را تعیین علامت میکنیم. در نهایت از روی جدول مجموعه جواب را مینویسیم.
مثال ۴: نامعادله \( \LARGE 3x^2-x \geq 2 \) را حل کنید؟
حل ۴:
ابتدا دو طرف را منهای 2 میکنیم که طرف دوم صفر شود سپس نامعادله از راه تعیین علامت حل میکنیم.
\( \LARGE 3x^2-x-2 \geq 0 \)
یعنی باید مقادیری از \( \Large x \) که این عبارت به ازای آنها مثبت یا صفر میشود را پیدا کنیم.
\( \LARGE 3x^2-x-2=0 \)
\( \LARGE \Delta =b^2-4ac \)
\( \LARGE \Delta =1+24=25 \)
\( \LARGE x=\frac{-b\pm \sqrt{\Delta}}{2a}=\frac{1\pm \sqrt{25}}{6} \)
\( \LARGE x_1=1,x_2=-\frac{2}{3} \)
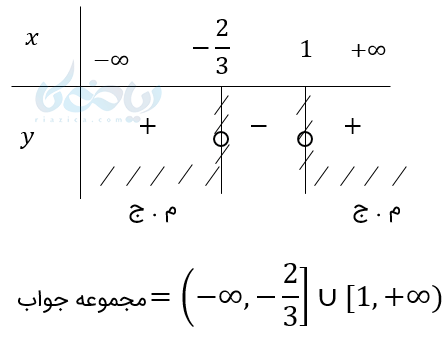
نکته: اگر در این نامعادله داشتیم \( \Large 3x^2-x-2>0 \) بازهها باز میشوند چون ریشهها جزء جواب نیستند.
مثال ۵: نامعادله \( \LARGE \frac{x^2-4}{2x-1} \leq 0 \) را حل کنید؟
حل ۵:
برای حل این نامعادله گویا نیز از تعیین علامت استفاده میکنیم و مقادیری از \( \Large x \) که به ازای آنها عبارت منفی باشد را پیدا میکنیم.
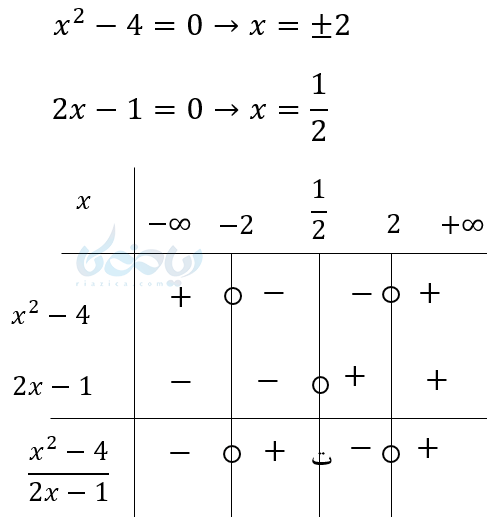
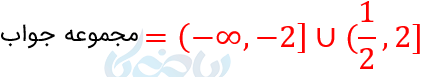
نکته: اعداد تعریف نشده همیشه در بازهها، باز نوشته میشوند.
مثال ۶: به ازای چه مقادیری از \( \Large m \) عبارت \( \Large y=mx^2+4x+1 \) همواره مثبت است؟
حل ۶:
میدانیم یک عبارت درجه دوم وقتی همواره مثبت است که دو شرط داشته باشد.
\( \LARGE \begin{cases} \Delta<0 \\ a>0\end{cases} \)
\( \LARGE \begin{cases} \Delta=16-4m<0 \\ a>0\end{cases} \)
\( \LARGE \rightarrow \begin{cases} 16<4m \rightarrow m>4 (1)\\ m>0(2)\end{cases} \)
دو نامعادله مقادیر \( \Large m \) اشتراک بین این دو نامعادله خواهد بود.
\( \LARGE (1) \cap (2) \rightarrow m>4 \)
پس به ازای \( \Large m \)های بزرگتر از 4 این عبارت همواره مثبت خواهد بود.
مثال ۷: برای چه مقادیری از \( \Large m \) عبارت \( \Large y=-x^2+mx-1 \) همواره منفی خواهد بود.
حل ۷:
\( \LARGE \begin{cases} \Delta<0 \\ a<0\end{cases} \)
\( \LARGE \begin{cases} \Delta=m^2-4<0 \\ -1<0\end{cases} \)
پس چون \( \Large a<0 \) است فقط جواب نامعادله \( \Large m^2-4<0 \) را بدست میآوریم. چون این نامعادله درجه دوم است و باید آن را تعیین علامت کنیم.

نامعادلههای قدرمطلقی
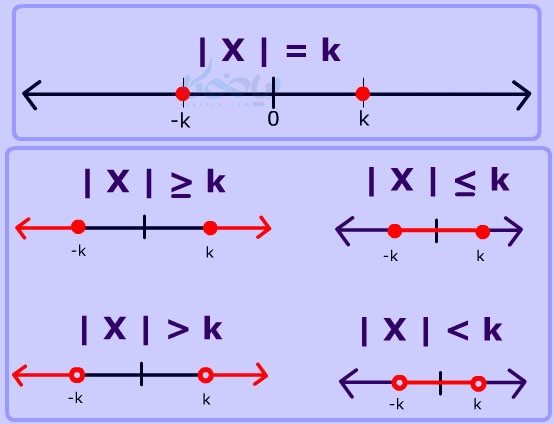
مفهوم قدرمطلق
نقطه 3 و 3- را روی اعداد حقیقی در نظر بگیرید.
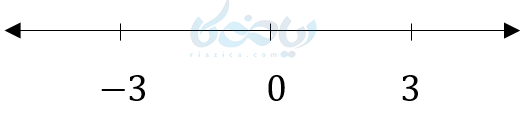
به نظر شما فاصله 3 تا مبدا (نقطه صفر) چقدر است؟ فاصله 3- تا مبدا چقدر است؟
جواب هر دو سوال 3 واحد میباشد این مفهوم را در ریاضی با نماد قدرمطلق نشان میدهیم. مینویسیم: \( \Large \left| 3 \right| = 3 \) یعنی فاصله 3 تا مبدا 3 واحد است و \( \Large \left| -3 \right| = 3 \) یعنی فاصله 3- تا مبدا نیز 3 واحد است. پس به طور کلی داریم:
\( \Large \left| x \right| \)همان فاصله \( \Large x \) تا مبدا، روی محور اعداد حقیقی است.حال نامعادله \( \Large \left| x \right| \leq 5 \) را در نظر بگیرید. مجموعه جواب این نامعادله در آموزش حل نامعادله شامل تمام نقاط روی محور اعداد حقیقی است، که فاصله آنها تا مبدا کمتر یا مساوی 5 واحد باشد.
یعنی:
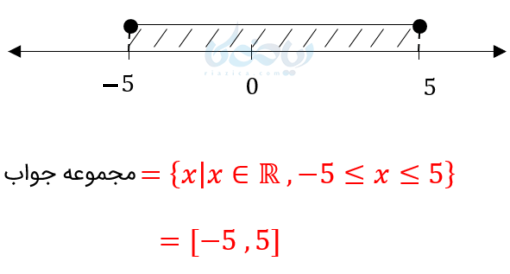
نامعادله \( \Large \left| x \right| \geq 5 \) را در نظر بگیرید. مجموعه جواب ابن نامعادله شامل تمام نقاط روی محور اعداد حقیقی است که فاصله آنها تا مبدا بیشتر یا مساوی 5 واحد باشد. یعنی:

پس به طور کلی داریم:
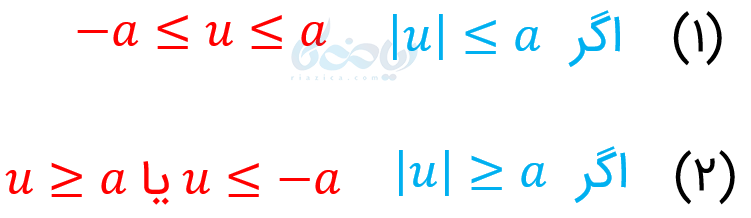
مثال ۸: نامعادلههای زیر را حل کنید؟
حل ۸:
مثال ۹: به ازای چه مقادیری از \( \Large m \) معادله \( \Large y=mx^2-mx-1 \) زیر محور \( \Large x \)ها قرار دارد؟ (صفحه 93 تمرین 3)
حل ۹:
آخر کلاس: جمعبندی آموزش حل نامعادله
در این نوشتار باهم آموزش حل نامعادله همراه با مثالهای متنوع یادگرفتیم. اما برای مهارت در حل انواع معادله نیاز به تمرین بیشتری است. که با حل نمونه سوالات موجود در سایت و کتاب درسیتان به این هدف است پیدا میکنید.
هر سوال از این بخش داشتید، زیر همین نوشتار در قسمت دیدگاهها برایمان بنویسید. کارشناسان ریاضیکا به شما پاسخ میدهند.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!



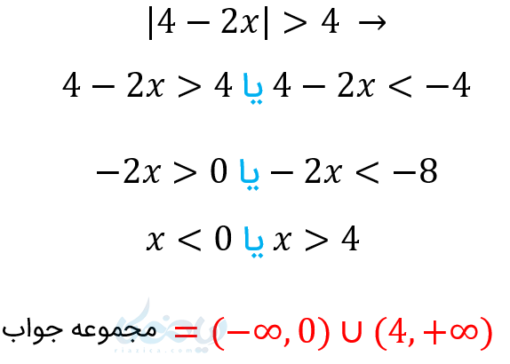


دوتا نامعدله میخوام حل کنید برام ممنون میشم
1 .ایکس +قدر مطلق ایکس کوچکتر مساوی یک دوم ایکس +سه
2. سه منهای دو قدر مطلق دو منهای ایکس کوچکتر مساوی یک + چهار ایکس
سلام پست مربوط به https://riazica.com/solving-inequalities/ و کامل بخونید میتوانید حل کنبد ممنونیم.
سلام
جواب: x=-6
قدر مطلق x سمت چپ نگه دارید ما بقی عبارت بره سمت راست
حالا عبارت به شکل >=|u| در می یاد.
سلام ببخشید توی مثال 7 چرا 0>-1 شد؟
با سلام دوست عزیز
این شرط دوم سوال می باشد که برقرار هست
عالی
ممنون از آموزش خوبتون
با سلام وعرض احترام
ممنون از لطف ونگاه پرانرژی شما
با عرض سلام در حل نامعادله چه کارهایی را نباید کرد به عنوان مثال طرفین وسطین مجاز است؟
یا سلام
اگر در مخرج کسرهای نامعادله عدد مثبت باشد طرفین وسطین مشکلی ندارد اما اگر متغیر باشد حق اینکار را نداریم
b^2_<-a^2-4/3a-1/3رو میشه لطفا راهنمایی کنید
با سلام
اصلا سوال مشخص نیست
با عرض سلام اگر در نامعادله۳=۳اتفاق بیافتد چه اتفاقی رخ میدهد؟
با سلام وادب
در این صورت معادله بی نهایت جواب دارد وبه ازای هر مقداری درست است
استاد بسیار ممنون هستم که به سوال بنده جواب دادید ایا در نامعادله قدرمطلقی که محدوده دارد هم اینگونه است ؟چون اعداد در ان محدوده ۳=۳هستند ودر خارج از ان محدوده این خاصیت را ندارند
سلام وقت بخیر من یک سوال داشتم که چرا در _۴ باز
سلام دوست عزیز
کدوم مثال؟
ممنون استاد بسیار مفید بود??
ممنون استاد بسیار مفید بود
با سلام وادب
خوشحالیم که مفید بوده
سلام استاد وقتتون بخیر وقتی بین دو قدر مطلق علامت جمع باشه کل عبارت کوچکتر مساوی ۵ باشد؛ مجموعه جواب چیست؟
با سلام وادب
ابتدا باید عبارت رو تعیین علامت کنید قدر مطلق رو بردارید بعد نامعادله رو حل کنید
داداش تو مثال ۵ تو جدول تعیین علامت x²_4 رو اشتباه تعیین علامت کردید
با سلام وادب
کجاش اشتباه هست ؟
سلام،عالی بودممنون فقط یه اشکال برام پیش اومد،پس ماتغیرجهت توعلامت رویکی توضربای مختلف العلامت ویکیم توتقسیم داریم؟
با سلام دوست عزیز
هر جا به منفی ضرب یا تقسیم بشه جهت نامعلدله عوض میشه