آموزش ریاضی پایه دهم
آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
ابتدا با یک مثال آموزش جایگشت ریاضی دهم را باهم یادبگیریم. سپس تمامی نکات و حالاتهایش را بررسی خواهیم کرد.
مثال ۱: فرض کنید سه مهره آبی، سبز و قرمز داریم. به چند طریق میتوان این سه مهره را کنار هم قرار داد؟
جواب ۱: طبق اصل ضرب که در آموزش اصل شمارش با آن آشنا شدیم، برای مهره اول 3 انتخاب به ازای هر کدام، برای مهره دوم 2 انتخاب و برای مهره سوم 1 انتخاب خواهیم داشت. یعنی:

به هر کدام یک از حالتهای قرار گرفتن مهرهها کنار هم یک جایگشت میگویند. پس تعداد جایگشت های 3 مهره رنگی مختلف 6 است.
تعریف جایگشت
اگر چند شئ مختلف داشته باشیم، به هر حالت چیدن (قرار گرفتن) آنها کنارهم یک جایگشت از آن اشیاء میگویند.
چند مثال مهم و جذاب از آموزش جایگشت
مثال ۲: 5 کتاب مختلف را به چند حالت میتوان در کتابخانه کنارهم قرارداد؟
حل ۲:
\( \LARGE 5 \times 4 \times 3 \times 2 \times 1 = 120 \)
مثال ۳: 6 مداد رنگی مختلف را به چند صورت در داخل جعبه مدادرنگی میتوان چید؟
حل ۳:
\( \LARGE 6 \times 5 \times 4 \times 3 \times 2 \times 1 \)
\( \LARGE = 720 \)
مثال ۴: دانش آموزان یک کلاس 15 نفری به چند صورت میتوانند در یک صف در مراسم صبحگاهی باشند؟
حل ۴:
\( \LARGE 15 \times 14 \times .. \times 3 \times 2 \times 1 \)
\( \LARGE = 15! \)
پس داریم:
اگر \( \Large n \) یک عدد طبیعی باشد، تعداد جایگشت های \( \Large n \) شئ متمایز به صورت زیر خواهد بود.
![]()
پس طبق این نماد (فاکتوریل) تعداد جایگشت های \( \Large n \) شئ متمایز برابر است با \( \Large n! \)
مثال ۵: تعداد جایگشت های عددهای 5 و 9 و 8 و 3 چند است؟
حل ۵:
\( \LARGE 4!= 4 \times 3 \times 2 \times 1 =24 \)
مثال ۶: تعداد جایگشت های حروف کلمه (مدرسه) چندتا است؟
حل ۶:
\( \LARGE 5!=5 \times 4 \times 3 \times 2 \times 1 \)
\( \LARGE = 120 \)
مثال ۷: علی 5 کتاب ریاضی و 3 کتاب شیمی مختلف دارد. او میخواهد آنها را در یک قفسه بچیند به طوریکه همیشه کتابهای شیمی کنارهم باشند. این کار به چند طریق امکانپذیر است؟
حل ۷: در اینجا چونکه باید کتابهای شیمی کنارهم باشند، آنها را یکی فرض میکنیم. پس 1 کتاب شیمی و 5 کتاب ریاضی داریم. در نتیجه تعداد جایگشت های آنها میشود !6. اما خود 3 کتاب شیمی هم میتوانند در کنارهم جابجا شوند. پس به ازای هر !6، !3 هم جایگشت کتابهای شیمی را داریم. در نتیجه جواب میشود:
\( \LARGE 6! \times 3! \)
مثال ۸: 7 نفر میخواهند در یک صف بایستند که دو نفر آنها با هم برادرند و قرار است یکی اول صف و دیگر در آخر صف قرار بگیرد، این کار به چند طریق ممکن است؟
حل ۸: غیر از دو برادر 5 نفر دیگر به !5 میتوانند در صف بایستند و خود دو برادر به !2 یا همان دو حالت در اول یا آخر صف قرار میگیرند، پس جواب میشود:
\( \LARGE 5! \times 2! \)
نکته آموزش جایگشت: اگر جایگشت \( \Large n \) شئ را بخواهیم که \( \Large m \) تا از آنها غیرمتمایز (یکی) باشند، تعداد جایگشت های آنها \( \huge \frac{n!}{m!} \) خواهد بود.
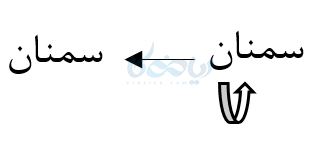
مثال ۹: تعداد جایگشتهای حروف کلمه (سمنان) چندتا است؟
حل ۹: سمنان شامل 5 حرف است. پس تعداد جایگشت های آن !5 خواهد بود. اما در آن دو حرف نون داریم که اگر در کلمهای فقط این دو حرف جابجا شوند کلمه جدیدی پدید نمیآورند. یعنی جابجایی آنها کلمه جدیدی نمیسازد، پس جواب میشود:
\( \LARGE \frac{5!}{2!}=60 \)
یعنی با حروف این کلمه 120 کلمه 5 حرفی میتواند نوشت که نصف آنها مثل هم هستند.
مثال ۱۰: با حروف کلمه (می سی سی پی) چند کلمه هشت حرفی میتوان نوشت؟
حل ۱۰:
\( \LARGE \frac{8!}{4! \times 2!}=60 \)
جایگشت \( \Large k \) شی از \( \Large n \) شی (ترتیب \( \Large k \) شی از \( \Large n \) شی)
فرض کنید 7 نفر هستند که از بین آنها میخواهیم 3 نفر انتخاب و آنها را به صف کنیم. چند حالت این کار امکان پذیر است؟ طبق اصل ضرب داریم:
بر اساس تعداد انتخابها
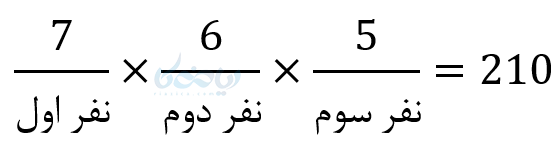
به 210 طریق این کار امکانپذیر است.
از طرفی داریم:
\( \LARGE \frac{7!}{4!}=\frac{7\times 6 \times 5 \times 4!}{4!} \)
\( \LARGE = 7\times 6 \times 5 \times = 210 \)
رابطه بالا را به صورت زیر هم میتوان نوشت:
\( \LARGE \frac{7!}{4!}=\frac{7!}{(7-3)!} \)
حاصل به دست آمده را از رابطه زیر میتوان نتیجه گرفت:
\( \LARGE P(7,3)=\frac{7!}{(7-3)!} \)
یعنی هرگاه بخواهیم از بین \( \Large n \) شئ تعداد جایگشت های \( \Large k \) شئ را انتخاب میکنیم، به طوریکه ترتیب قرارگرفتن آنها برایمان مهم باشد، از رابطه زیر استفاده میکنیم. ذکر این نکته مهم است که در مبحث آموزش جایگشت به رابطه زیر رابطه ترتیب هم میگویند.
\( \LARGE P(n,k)=\frac{n!}{(n-k)!} \)
و میخوانیم ترتیب قرار گرفتن \( \Large k \) شئ از بین \( \Large n \) شئ یا تعداد جایگشت \( \Large k \) شئ از بین \( \Large n \) شئ.
نکته مهم آموزش جایگشت: البته به شما توصیه میکنم که در این موارد بهتر است از همان اصل ضرب استفاده کنید. فقط در مسائل دقت کنید ترتیب قرارگرفتن اشیا مهم است یا اینکه فقط مسئلهٔ انتخاب کردن است.
مثال ۱۱: با حروف کلمه \( \Large flower \) چند کلمه (بدون تکرار)
الف) 6 حرفی میتوان نوشت؟
\( \LARGE 6! \)
ب) 3 حرفی میتوان نوشت؟
\( \LARGE P(6,3)=\frac{6!}{3!} \)
\( \LARGE =\frac{6 \times 5 \times 4 \times 3 !}{3!} =120 \)
ج) 6 حرفی که با \( \Large f \) شروع و به \( \Large r \) ختم شود؟
چون حروف \( \Large f , r \) در جابجاییها شرکت ندارند.
\( \LARGE \frac{1}{f} \times 4 \times 3 \times 2 \times 1 \times \frac{1}{r} \)
\( \LARGE=4! \)
یعنی تعداد جایگشتها 4 شی را میخواهیم
د) 6 حرفی که \( \Large f , l \) کنارهم باشند؟
\( \Large f , l \) را یک حرف در نظر میگیریم با 4 حرف دیگر تعداد جایگشتشان !5 میشود و تعداد جایگشت خود \( \Large f \) و \( \Large l \) نیز !2 است.\( \LARGE 2! \times 5! \)
و) 6 حرفی که واژه \( \Large (flo) \) در آن وجود داشته باشد؟
\( \LARGE 4! \)
چون \( \Large flo \) به همین شکل قرار است در کلمات ظاهر شود. پس همراه 3 حرف دیگر 4 شی محسوب میشوند که تعداد جایگشت آنها !4 میشود.
زنگ آخر کلاس آموزش جایگشت
با هم در ریاضیکا آموزش جایگشت را خواندیم. مطالبی از تعریف جایگشت، جایگشت \( \Large k \) شئ از \( \Large n \) شئ (ترتیب \( \Large k \) شئ از \( \Large n \) شئ) را یاد گرفتیم.
مطالب دیگری از آموزش ریاضی دهم میتوانیم در همین سایت بخوانید. درصورتیکه هر سوالی از این آموزش داشتید میتوانید آن را زیر همین آموزش برای ما بنویسید. کارشناسان ریاضیکا حتماً به سوالات شما عزیزان پاسخ میدهند. موفق و شاد باشید 🙂
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!





مرسی واقعا عالی بود و جواب سوالم رو بعد از کلی گشتن داخل سایت های مختلف اینجا پیدا کردم
ضمن عرض سلام
خیلی خوشحالیم که این آموزش براتون مفید بوده
برای مطالعه کامل آموزشهای پایه دهم میتوانید به آدرس https://riazica.com/series/math-10th-grade/ مراجعه کنید.
با حروف کلمهperusalچند جایگشت ۷حرفی بدون تکرار میتوان نوشت که به حرف eختم شود و حرنفeruکنار هم باشند
با سلام وعرض ادب
میشود چهار فاکتوریل ضربدر سه فاکتوریل
سلام. اگه بخواهیم 5 نفر رو به صف کنیم به طوری که دو نفر از این ها کنار هم نباشند چطور میشه محسبه کرد؟
یا سلام واحترام
کل حالتها رو منهای وقتی دونفر کنار هم هستن کنبد یعنی پنج فاکتوریل منهای چهار فاکتوریل ضربدر ۲
سلام اگه بگه با عددای
۱ ۱ ۱ ۲ ۲ ۳ ۳
جایگشت هفت رقمی بنویسیم باید چیکارکنیم؟
همینطور اگه بگه با عددای ۱ ۱ ۱ ۲ ۲ جایگشت سه رقمی بنویسید؟
مرسی از سایت عالیتون
با سلام وعرض ادب
جایگشت اینها میشه هفت فاکتوریل ولی چون سه تا یک ودوتا سه داریم جواب را تقسیم بر سه فاکتوریل ضربدر دو فاکتوریل ضربدر دو فاکتوریل میکنیم دومی رو همین طور خودتون حساب کنید
تعداد جایگشت های ۲۶ حرف انگلیسی را بیابید بع طوری که هیچکدام از کلمات math Runs From joe در آن ظاهر نشود؟
سلام .چطوری میشه اثبات کرد تعداد جایگشت های r از n کهrشیء کوچکتر و مساوی nشیء برابر باشه با n فاکتوریل به روی nمنهایrفاکتوریل؟
با سلام
اینجا نمیشه اثبات کرد
لطفا جواب ممنون میشم
چه تعداد جایگشت های حروف کلمه summit شامل یکی از الگو های it و sum میباشد؟
سلام. عالييييي
سلام.
مسئله گفته:از میان تعدادی کتاب،دو کتاب را انتخاب میکنیم و در قفسه میچینیم.این کار را به۳۸۰روش میتوان انجام داد.تعداد کتاب ها چندتاست؟
میشه لطفا بگین چی میشه؟
با سلام دوست عزیز
میشه جایگشت دو شی از میان n شی که از راه معادله قابل حل هست
با سلام و وقت بخیر.
۳ کتاب ریاضی و ۴ کتاب شیمی را به چند طریق میتوان در یک قفسه چید به طوری که همه کتابهای شیمی کنار هم باشند، ولی همه کتابهای ریاضی کنار هم نباشند؟
ممنون از راهنمایی شما
فرشته گفته:
با سلام و وقت بخیر.
چهارفاکتوریل ضربدر چهارفاکتوریل میشه۵۷۶ که در بین گزینه ها نیست!
۳ کتاب ریاضی و ۴ کتاب شیمی را به چند طریق میتوان در یک قفسه چید به طوری که همه کتابهای شیمی کنار هم باشند، ولی همه کتابهای ریاضی کنار هم نباشند؟
۱)۲۸۸ ۲)۴۳۲ ۳)۳۶۰ ۴)۱۴۴
ممنون از شما
144 فکر کنم
باسلام درسته برا کتاب اول که حتما ریاضی هست ۳تا انتخاب داریم بعد چهار تا شیمی که میشه چهار فاکتوریل بعدی ریاضی دوت انتخاب وبعد ریاضی یکی انتخاب که حاصلضرب میشه ۱۴۴
گزینه 1
البته مطمعن نیستم
درسته
سلام یه سوال تعداد دنباله های ده عددی حروف abcd که حرف a دوبار و سایر حروف یک بار ظاهر شوند چند است
(سلام + خیلی عالی و مفید بود + مرسی)!
با سلام دوست عزیز
ممنون از نظر خوب شما
6 کتاب ادبیات متمایز و 2 کتاب شیمی متمایز را به چند طریق می توان در یک قفسه کنار هم چید به طوریکه 2 کتاب ادبیات بین 2 کتاب شیمی قرار گیرد؟
!6×!2×4=960
با سلام خوب بود.خیلی شبهات ومجهولیات من رفع شد.
خدا رو شکر که مغید بوده برای شما
سلام ، یک سوال :شخصی از هر کدام از سکه های یک،دو،سه،چهار،پنج،شش،هفت،هشت،نه و ده هزار تومانی،یک عدد دارد به چند روش می توان این ده سکه را بین 3 نفر تقسیم کرد ؟که مجموع هر گروه یکسان باشد .
با سلام اگر بخوایم با دو حرف AB یک ترکیب سه تایی با حالت مجاز بودن تکرار بنویسیم چند تا میشه
سه حرف هر حرف دو حالت داره پس میشه ۲×۲×۲که میشه هشت حالت ولی دوحالت هست که فقط حرف AوB هست که این دوحالت بره کنار میشه شش تا
البته در چیزی که شما نوشتی اینطور به نظر میاد که هر دو حرف باید باشن وگرنه همون ۸ میشه
مثال 11 قسمت ب و ج رو متوجه نشدم میشه لطف کنید بیشتر توضیحش بدین