آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!

یکی دیگر از دنباله‌های دارای الگو که از پرکاربردترین دنباله ها در ریاضیات میباشد  دنباله هندسی است که در شاخه‌های مختلف ریاضی و زیست و غیره کاربرد زیادی دارد. در این نوشتار قصد داریم باهم مبحث دنباله هندسی را همراه با مثال‌های متنوع یاد بگیریم.

تعریف دنباله هندسی

در آموزش دنباله هندسی برای نوشتن هر جمله به غیر از جمله اول، باید جملهٔ قبلی را در یک مقدار ثابت ضرب کرد. در ریاضیات به این مقدار ثابت قدر نسبت می‌گویند و آن را با حرف \( \Large r  \) نمایش می‌دهند. قدر نسبت یا \( \Large r  \) می‌تواند هر عدد حقیقی مخالف صفر باشد.

\( \LARGE r \in \mathbb{R} , r \neq 0 \)

مثال 1: یک دنباله هندسی بنویسید که جمله اول آن 5 و قدر نسبت آن 2 باشد.

حل 1:

\( \LARGE \begin{cases} a_1 = 5 \\ r = 2 \end{cases}  \)

\( \LARGE 5 , 10 , 20 , 40 , 80 , … \)

تشخیص یک دنباله هندسی

در آموزش دنباله هندسی برای تشخیص آن دنباله کافیست دو جفت از جملات متوالی دنباله را به هم تقسیم کنیم. مثلاً:

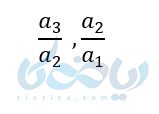
اگر به یک مقدار ثابت برسیم یعنی دنباله اعداد ما یک دنباله هندسی را تشکیل می‌دهند.

مثال 2: آیا دنباله زیر یک دنباله هندسی است؟

\( \LARGE 4 , 2 , 1 , \frac{1}{2} , … \)

حل 2:

\( \LARGE 4 , 2 , 1 , \frac{1}{2} , … \)

\( \LARGE \begin{cases} \frac{a_2}{a_1} = \frac{2}{4} = \frac{1}{2} \\ \frac{a_3}{a_2} = \frac{1}{2} \end{cases}  \)

پس دنبالهٔ زیر یک دنباله هندسی است.

فرمول جمله عمومی دنباله هندسی

فرض کنید اعداد زیر جملات متوالی یک دنباله هندسی باشند:

\( \LARGE a_1 , a_2 , a_3 , … , a_n , … \)

طبق تعریف دنباله هندسی داریم:

پس طبق آموزش دنباله هندسی جمله عمومی این دنباله از رابطهٔ زیر بدست می‌آید:

\( \LARGE a_n = a_{1}r^{n-1} \)

مثال 3: جمله عمومی دنباله زیر را بنویسید. سپس جمله دهم آن را محاسبه کنید؟

\( \LARGE 1 , 3 , 9 , 27 , … \)

حل 3:

\( \LARGE 1 , 3 , 9 , 27 , … \)

\( \LARGE \begin{cases} a_1 = 1 \\ r = 3 \\ a_{10} = ? \end{cases}  \)

\( \LARGE a_n = a_{1}r^{n-1} \)

\( \LARGE a_n = 1 \times 3^{n-1} \)

\( \LARGE a_{10} = 3^9 \)

نکته ۱: همانطور که ملاحظه می‌کنید وقتی \( \Large r  \) یک عدد مثبت بزرگتر از ۱ و جمله اول نیز مثبت باشد، دنباله صعودی و رشد جملات دنباله خیلی سریع است. به همین دلیل در مبحث آموزش دنباله هندسی ، به دنباله هندسی تصاعد هندسی نیز گفته می‌شود.

مثال 4: جمله چندم دنباله زیر 1024 است؟

\( \LARGE 2 , 4 , 8 , … \)

حل 4:

\( \LARGE 2 , 4 , 8 , … \)

\( \LARGE \begin{cases} a_1 = 2 \\ r = 2 \\ a_n = 1024 \rightarrow n = ? \end{cases}  \)

\( \LARGE a_n = a_{1}r^{n-1} \)

\( \LARGE 1024 = 2 \times 2^{n-1} \)

\( \LARGE 512 = 2^{n-1} \)

\( \LARGE 2^9 = 2^{n-1} \)

\( \LARGE 9 = n-1 \rightarrow n = 10 \)

پس جمله دهم دنباله 1024 است.

مثال 5: دنباله زیر را در نظر بگیرید و جمله بیستم آن را محاسبه کنید.

\( \LARGE 3 , 1 , \frac{1}{3} , \frac{1}{9} , … \)

حل 5:

\( \LARGE 3 , 1 , \frac{1}{3} , \frac{1}{9} , … \)

\( \LARGE \begin{cases} a_1 = 3 \\ r = \frac{1}{3} \\ a_{20} = ? \end{cases}  \)

\( \LARGE a_n = a_{1}r^{n-1} \)

\( \LARGE a_{20} = a_{1}r^{19} \)

\( \LARGE a_{20} = 3 \times (\frac{1}{3})^{19} \)

\( \LARGE a_{20} = \frac{1}{3^{18}} \)

نکته ۲: در مثال ۳ و ۴ چون قدر نسبت عدد مثبت بزرگتر از یک و جمله اول مثبت بود دنباله صعودی شد و رشد زیادی کرد. در مثال 5 که قدر نسبت عدد مثبت کوچکتر از یک و جمله اول نیز مثبت  است دنباله، یک دنباله نزولی است که جملات دنباله به صفر نزدیک می‌شوند.

مثال 6: در یک دنباله هندسی جمله سوم 18 و جمله ششم 486 است. این دنباله را مشخص کنید.

حل 6:

\( \LARGE \begin{cases} a_3 = 18 \\ a_6 = 486  \end{cases}  \)

\( \LARGE \rightarrow  \begin{cases} a_3 = a_{1}r^{2} \\ a_6 = a_{1}r^{5}  \end{cases}  \)

این هم یک دستگاه دو مجهولی است. اما چون بین مجهول‌ها عمل ضرب وجود دارد، برای حل دستگاه دو طرف تساوی را به هم تقسیم می‌کنیم.

(البته جمله شماره بیشتر به جمله شماره کمتر)

\( \LARGE \frac{a_{1}r^5}{a_{1}r^2} = \frac{486}{18}  \)

\( \LARGE r^3 = 27  \)

\( \LARGE r = 3  \)

حال باید جمله اول را پیدا کنیم:

\( \LARGE \begin{cases} a_3 = 18 \\ r = 3  \end{cases}  \)

\( \LARGE a_3 = a_{1} \times r^{2} \)

\( \LARGE 18 = a_{1} \times 3^{2} \)

\( \LARGE a_1 = 2 \)

پس دنباله به این صورت است:

\( \LARGE 2 , 6 , 18 , … \)

مثال ۷: جمع بیست جمله اول دنباله زیر را حساب کنید. (فصل اول ریاضی دهم – تمرین ۵ ویرایش ۱۳۹۸)

\( \LARGE 2 , 4 , 8 , …  \)

حل ۷:

آموزش دنباله هندسی : واسطه هندسی

وقتی سه عدد متوالی \( \Large a  \) , \( \Large b  \) , \( \Large c  \) را داریم، به طوری که آن‌ها تشکیل یک دنباله هندسی بدهند، در این صورت \( \Large b  \) را واسطه هندسی بین \( \Large a  \) , \( \Large c  \) می‌نامند و داریم:

\( \LARGE \begin{cases} r= \frac{b}{a} \\ r= \frac{c}{b} \end{cases}   \)

\( \LARGE \rightarrow  \frac{b}{a} = \frac{c}{b}  \)

\( \LARGE b^2 = ac  \)

یعنی مجذور جمله وسطی برابر است با حاصلضرب جمله اول و سوم.

مثال 8: مقدار x را چنان تعیین کنید که دنباله زیر یک دنباله هندسی باشد.

\( \LARGE x , x – 3 , x + 1    \)

حل 8:

\( \LARGE x , x – 3 , x + 1  \)

\( \LARGE (x – 3)^2 = x(x + 1)  \)

\( \LARGE x^2 – 6x + 9 = x^2 + x  \)

\( \LARGE -7x = -9  \)

\( \LARGE x = \frac{9}{7}  \)

حال اگر بین دو عدد بیش از یک واسطه هندسی بخواهیم به روش زیر عمل می کنیم.

مثال 9: بین دو عدد 3 و 48 سه واسطه هندسی پیدا کنید.

حل 9:

\( \LARGE 3 , … , … , … , 48  \)

\( \LARGE \begin{cases} a_1 = 2 \\ a_5 = 48 \end{cases}  \)

\( \LARGE a_5 = a_{1}r^4 = 48 \)

\( \LARGE 48 = 3 \times r^4  \)

\( \LARGE  r^4 = 2^4 \rightarrow r = \pm 2  \)

\( \LARGE 3 , \pm 6 , 12 , \pm 24 , 48  \)

نکته ۳: وقتی یک دنباله هندسی را داریم می‌توانیم برای بدست آوردن قدر نسبت از رابطه زیر استفاده کنیم. در این رابطه \( \Large a_m , a_n \) جملات داده شده‌اند.

نکته ۴: دنباله ثابت هم جزء دنباله های هندسی و هم حسابی محسوب می‌شود.

حل ویدیویی یک نمونه سوال ریاضی دهم از مبحث آموزش دنباله هندسی

در این ویدیو آموزشی یک نمونه سوال از مبحث دنباله هندسی برای شما عزیزان حل شده است. برای دانلود سایر سوالات به صفحه نمونه سوال ریاضی دهم با جواب مراجعه فرمایید.

کلام آخر کلاس آموزش دنباله هندسی

تو این نوشتار در مورد آموزش دنباله هندسی باهم صحبت کردیم. یاد گرفتیم که چطور می‌توان قدر نسبت یک دنباله هندسی را محاسبه کرد. همچنین یاد گرفتیم که با داشتن قدر نسبت جملات دلخواه یک دنباله هندسی را بدست آوریم. در نهایت آموزش‌هایمان را با مثال‌های متنوع باهم مرور کردیم.

در صورتیکه هر سوالی در این رابطه با آموزش دنباله هندسی یا آموزش ریاضی پایه دهم داشتید، در زیر همین قسمت در بخش دیدگاه‌ها مطرح کنید. ما در ریاضیکا اینجا هستیم تا به سوالات شما پاسخ دهیم.