آموزش ریاضی پایه دهم
تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
فروردین
تعیین علامت عبارت های جبری کاربرد زیادی در حل نامعادلات درجه اول و دوم، نامعادلات قدرمطلقی و تعیین دامنه توابع لگاریتمی و رادیکالی دارد. بنابراین در آموزش پیشرو سعی کردیم کامل‌ترین و جامع‌ترین آموزش تعیین علامت عبارت های جبری را ارائه دهیم تا باهم به خوبی آن را فرا بگیریم.
تعیین علامت عبارت های درجه اول
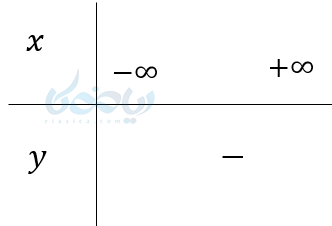
در آموزش ریاضی دهم یاد می‌گیریم که وقتی ما از اعداد صحبت میکنیم علامت آنها مشخص است. مثلاً 5 علامتش مثبت، 7- علامتش منفی و صفر نه مثبت نه منفی است. امّا وقتی مثلاً عبارت \( \Large 2x+1 \) را در نظر بگیرید. می‌توانیم بگوییم علامت این عبارت چیست؟ چون در این عبارت متغیر \( \Large x \) را داریم و بسته به اعدادی که جای \( \Large x \) قرار می‌گیرند علامت این عبارت تغییر می‌کند. مثلاً به ازای \( \LARGE -\frac{1}{2} \) صفر، به ازای 3 مثبت و به ازای 3- منفی میشود. اگر نمودار این خط را رسم کنیم داریم:
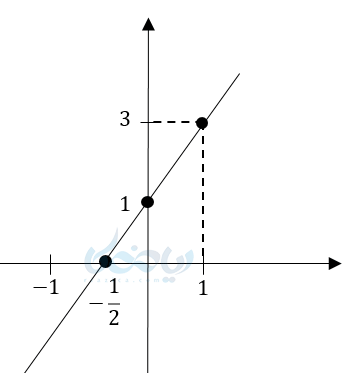
در این نمودار می‌بیند که این خط محور \( \Large x \)ها را در نقطه \( \LARGE -\frac{1}{2} \) قطع کرده ؛ (ریشه معادله). در این نقطه \( \Large y\) صفر است و به ازای مقادیر بیشتر از \( \LARGE -\frac{1}{2} \) ، خط بالای محور \( \Large x \)ها قرار دارد و مثبت است و به ازای مقادیر کمتر از \( \LARGE -\frac{1}{2} \) خط زیر محور \( \Large x \)ها قرار دارد. یعنی \( \Large y \) منفی است. اگر این اطلاعات را داخل یک جدول تعیین علامت بنویسیم داریم:
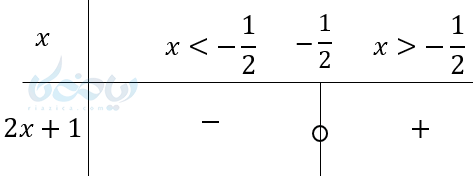
یک مثال برای فهم بهتر تعیین علامت عبارت ها
\( \Large y = -2x + 6 \) اگر نمودار این خط را رسم کنیم داریم: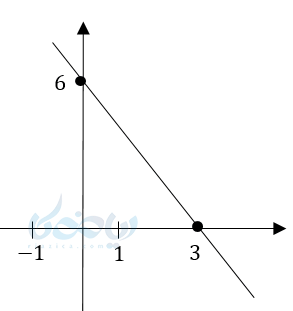
در این مثال نمودار محور \( \Large x \)ها را در نقطه 3 که ریشه این معادله است قطع کرده و به ازای مقادیر بیشتر از 3 نمودار زیر محور \( \Large x \)ها قرار دارد و \( \Large y \) منفی است و به ازای مقادیر بیشتر از 3، نمودار بالای محور \( \Large x \)ها است. پس \( \Large y \) مثبت است.
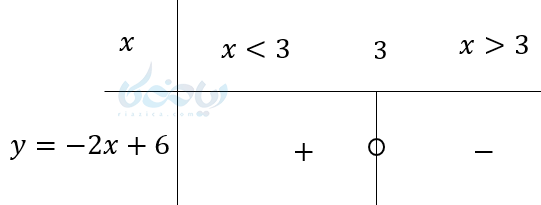
اگر به این دو مثال دقت کنید در می‌یابید که اولاً ریشه معادله مرز بین مقادیر مثبت و منفی است. در مثال اول که ضریب \( \Large x \) مثبت بود مقادیر کوچکتر از ریشه منفی (مخالف \( \Large a \)) و بزرگتر از ریشه مثبت (موافق \( \Large a \)) است.
در مثال دوم مقادیر کوچکتر از ریشه مثبت (مخالف \( \Large a \)) و مقادیر بزرگتر از ریشه منفی (موافق \( \Large a \)) هستند. پس برای تعیین علامت عبارت های جبری درجه اول، ابتدا ریشه عبارت را بدست می‌آوریم (آن را مساوی صفر قرار می‌دهیم). سپس در جدول مقادیر کمتر از ریشه مخالف \( \Large a \) (ضریب \( \Large x \)) و مقادیر بیشتر از ریشه موافق \( \Large a \) خواهند بود.
مثال ۱: عبارت \( \Large y = 3 -4x \) را تعیین علامت کنید؟
چند استثناء در مورد مشخص کردن علامت عبارات درجه اول
۱. اگر عبارت درجه اول داخل قدر مطلق باشد به جزء ریشه به ازای همه مقادیر مثبت خواهد بود.
مثال ۲ تعیین علامت عبارت های جبری: \( \Large y = \left| -x + 3 \right| \) را تعیین علامت کنید.
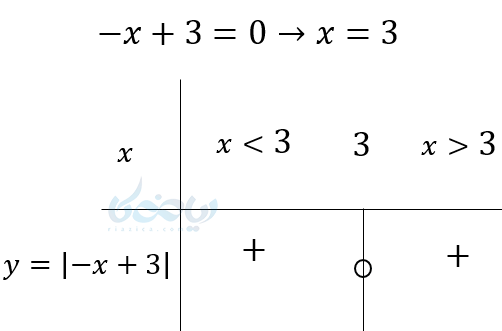
نکته ۱ تعیین علامت عبارت های جبری: اگر پشت قدرمطلق منفی باشد به جز ریشه به ازای همه مقادیر منفی خواهد بود.
مثال ۳ تعیین علامت عبارت های جبری: \( \Large y = -\left| 4 – 2x \right| \) را تعیین علامت کنید.
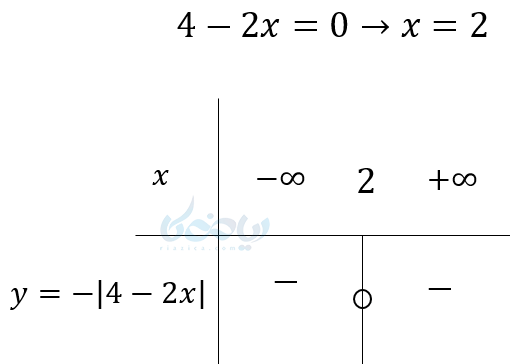
به جای \( \Large x>2 , x<2 \) علامت \( \Large +\infty , -\infty \) هم می‌توانیم قرار دهیم که راحت‌تر است.
۲. اگر عبارت درجه اول دارای توان زوج باشد.
در اینصورت مانند قدرمطلق به ازای همه مقادیر مثبت است. مگر اینکه پشت پرانتز منفی باشد که در اینصورت به ازای همه مقادیر منفی خواهد بود.
مثال ۴ تعیین علامت عبارت های جبری: \( \Large y = (-2x-1)^2 \) را تعیین علامت کنید.
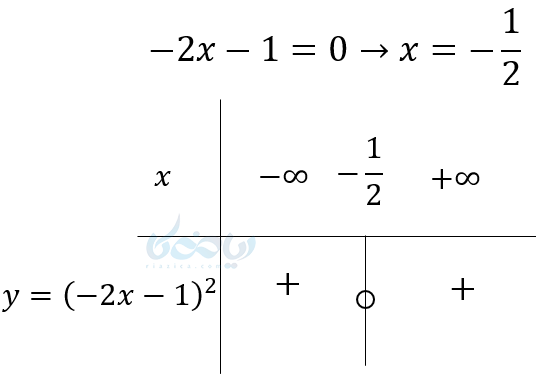
مثال ۵: \( \Large y = -(3x+1)^4 \) را تعیین علامت کنید.
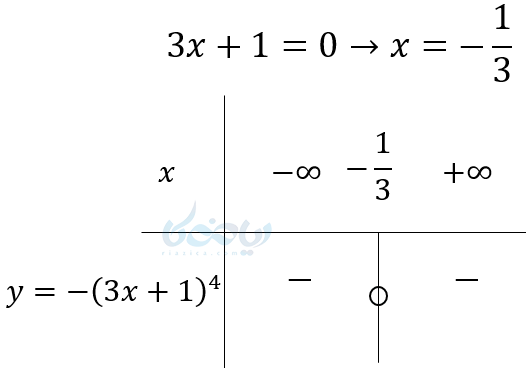
۳. اگر عبارت درجه اول دارای توان فرد باشد.
اگر عبارت درجه اول دارای توان فرد باشد، این توان را نادیده گرفته و به حالت معمولی آن را تعیین علامت میکنیم.
مثال ۶ تعیین علامت عبارت های جبری: \( \Large y = (-4-2x)^3 \) را تعیین علامت کنید؟
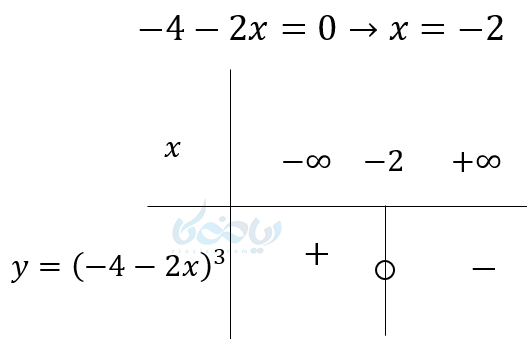
نکته ۲ تعیین علامت عبارت های جبری: اگر در این مواقع پشت پرانتز علامت منفی بود و بعد از تعیین علامت منفی را در جدول تاثیر می‌دهیم.
مثال ۷ تعیین علامت عبارت های جبری: \( \Large y = -(x-4)^5 \) را تعیین علامت کنید.
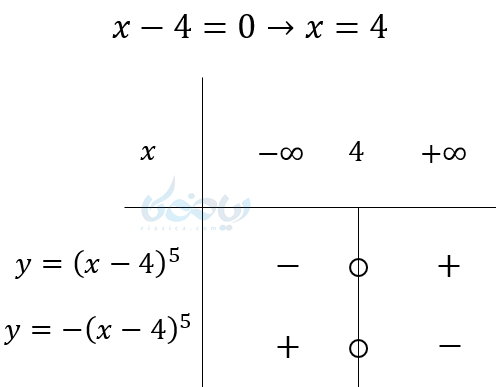
۴. دو عبارت درجه اول که در هم ضرب یا به هم تقسیم شده‌اند.
در این مواقع ریشه هر عبارت را بدست آورده ولی در یک جدول به ترتیب از کوچک به بزرگ می‌نویسیم. سپس هر عبارت را جداگانه تعیین علامت کرده (سطری) و در نهایت علامت‌های ستون‌ها را در هم ضرب میکنیم.
مثال ۸ تعیین علامت عبارت های جبری: \( \Large y = (x-2)(3-4x) \) را تعیین علامت کنید.
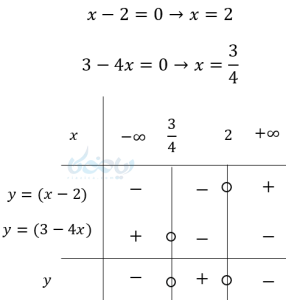
این جدول به ما نشان می‌دهد که اگر اعداد بین \( \LARGE \frac{3}{4}<x<2 \) را به جای \( \Large x \) قرار دهیم، عبارت مثبت و اگر مقادیر بیشتر از 2 و کمتر \( \LARGE \frac{3}{4}\) را قرار دهیم عبارت منفی میشود.
مثال ۹ تعیین علامت عبارت های جبری: \( \Huge y = \frac{\left| -x-3 \right|}{5-x} \) را تعیین علامت کنید.
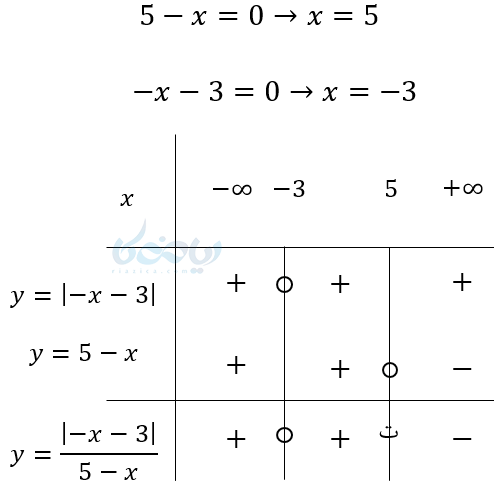
دقت کنید در این مثال 5 ریشه مخرج است. همچنین می‌دانیم اگر مخرج کسری صفر باشد، آن کسر تعریف نشده است. برای همین روی خط مربوط به عدد 5 (ت) که مخفف (تعریف نشده) است قرار می‌دهیم.
تعیین علامت عبارتهای درجه دوم
می‌دانیم عبارتهای درجه دوم را وقتی مساوی صفر قرار می‌دهیم و ریشه‌هایشان را پیدا میکنیم به 3 دسته تقسیم می‌شوند:
- وقتی \( \LARGE \Delta > 0 \) است که دو ریشه داریم.
- وقتی \( \LARGE \Delta = 0 \) که یک ریشه داریم.
- وقتی \( \LARGE \Delta < 0 \) که ریشه نداریم.
۱. تعیین علامت عبارات درجه دومی که \( \Large \Delta > 0 \) و دو ریشه دارند.
اگر نمودار این دسته از معادلات درجه دوم را رسم کنیم، نمودار آنها (سهمی) محور \( \Large x \)ها را در دو نقطه قطع می‌کند و اگر \( \Large a>0 \) باشد نمودار به صورت زیر است:
اگر \( \Large a<0 \) باشد نمودار به صورت زیر خواهد بود:
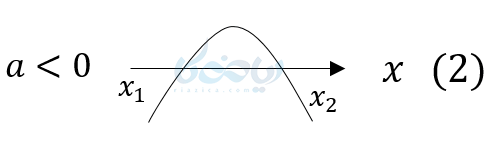
اگر فرض کنیم \( \Large x_1 , x_2 \) ریشه‌های معادله باشند، می‌بینید مقادیر بین دو ریشه علامتشان مخالف \( \Large a \) است. در نمودار (1) \( \Large a>0 \) است ولی مقادیر بین دو ریشه زیر محور \( \Large x \)ها قرار دارند و منفی هستند.
ولی مقادیر کمتر یا بیشتر از دو ریشه بالای محور \( \Large x \)ها قرار دارند و با علامت \( \Large a \) موافقند. در نمودار شماره (2) نیز همین اتفاق افتاده است پس نتیجه می‌گیریم برای تعیین علامت عبارتهای درجه دوم ابتدا \( \Large \Delta \) را پیدا کرده اگر \( \Large \Delta >0 \) بود ریشه‌ها یعنی \( \Large x_1 , x_2 \) را پیدا میکنیم و به صورت جدول زیر تعیین علامت میکنیم.
مثال ۱۰: \( \Large y = x^2-5x+6 \) را تعیین علامت کنید.
\( \LARGE x^2 – 5x +6 =0 \)
\( \LARGE \Delta = b^2 – 4ac \)
\( \LARGE \Delta = 25-24=1>0 \)
\( \LARGE x=\frac{-b\pm \sqrt{\Delta}}{2a}=\frac{5\pm \sqrt{1}}{2} \)
\( \LARGE x_1=3 , x_2=2 \)
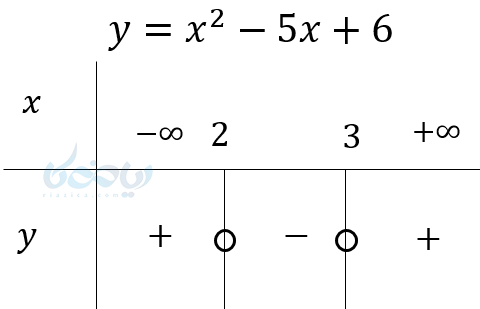
نکته ۳ تعیین علامت عبارت های جبری: اگر عبارت داده شده تجزیه پذیر باشد، می‌توان آن را تجزیه و به دو عبارت درجه اول تبدیل و از روش عبارتهای درجه اول آن را تعیین علامت کرد. اما روش بالا کوتاه‌تر و راحت‌تر است.
مثال ۱۱: \( \Large y = -2x^2+3x-1 \) را تعیین علامت کنید.
\( \LARGE -2x^2 +3x-1 =0 \)
\( \LARGE \Delta = b^2 – 4ac \)
\( \LARGE \Delta = 9-8=1>0 \)
\( \LARGE x=\frac{-b\pm \sqrt{\Delta}}{2a}=\frac{-3\pm \sqrt{1}}{-4} \)
\( \LARGE x_1=1 , x_2=\frac{1}{2} \)
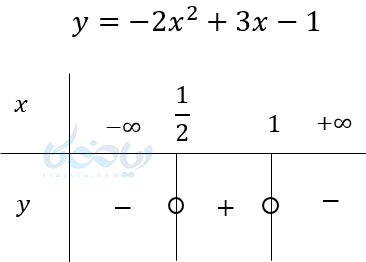
۲. تعیین علامت عبارات درجه اولی که \( \Large \Delta= 0 \) و یک ریشه دارند.
اگر یک عبارت درجه دوم را ریشه‌یابی کنیم \( \Large \Delta=0 \) و یک ریشه داشته باشد، نمودار آن در یک نقطه مماس بر محور \( \Large x \)ها خواهد بود و داریم:
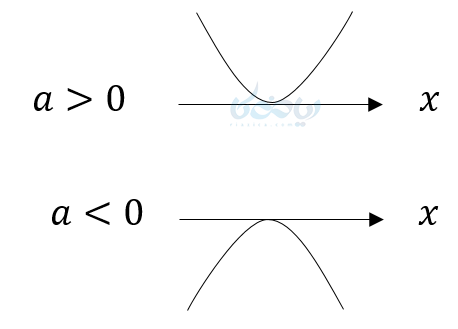
همانطور که ملاحظه می‌کنید وقتی \( \Large \Delta=0 \) است و یک ریشه دارد:
- اگر \( \Large a>0 \) باشد نمودار کاملاً بالای محور \( \Large x \)ها است پس به ازای همه مقادیر جز ریشه مثبت است.
- اگر \( \Large a<0 \) باشد نمودار کاملاً زیر محور \( \Large x \)ها قرار دارد و به ازای همه مقادیر جز ریشه‌های منفی است. یعنی هم علامت \( \Large a \).
- پس می‌توانیم بگوییم در این مواقع که \( \Large \Delta=0 \) و یک ریشه داریم به جز ریشه به ازای بقیه مقادیر علامت همواره موافق \( \Large a \) است.
مثال ۱۲ تعیین علامت عبارت های جبری: \( \Large y = x^2-4x+4 \) را تعیین علامت کنید.
\( \LARGE x^2-4x+4=0 \)
\( \LARGE (x-2)^2=0 \)
\( \LARGE x=2 \)
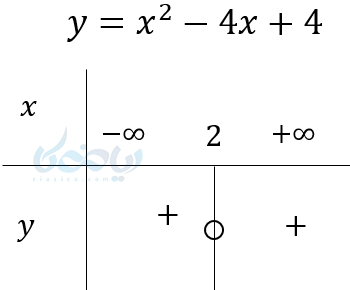
مثال ۱۳: \( \Large y = -x^2+6x+9 \) را تعیین علامت کنید.
\( \LARGE -x^2+6x+9 =0 \)
\( \LARGE \Delta = b^2 – 4ac \)
\( \LARGE \Delta = 0 \)
\( \LARGE x=-\frac{b}{2a}=\frac{-6}{-2} \)
\( \LARGE x=3 \)
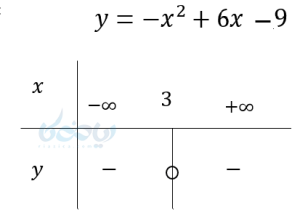
۳. تعیین علامت عبارات درجه دومی که \( \Large \Delta< 0 \) و ریشه ندارند.
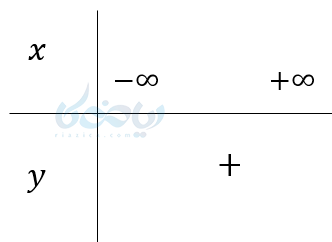
در تعیین علامت عبارت های جبری یاد می‌گیریم، عبارتهای درجه دومی که در آنها \( \Large \Delta<0 \) و ریشه ندارند نمودار آنها محور \( \Large x \)ها را قطع نمی‌کند و نمودار آنها:
- اگر \( \Large a>0 \) بالای محور \( \Large x\)ها است
- اگر \( \Large a<0 \) باشد زیر محور \( \Large x \)ها است. یعنی به ازاء جمیع مقادیر علامت عبارت هم علامت \( \Large a \) است.
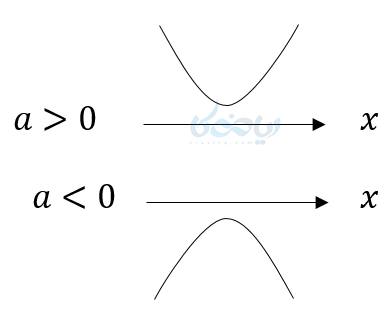
پس داریم:
مثال ۱۴: \( \Large y=3x^2-ax+2 \) را تعیین علامت کنید.
\( \LARGE 3x^2-ax+2 =0 \)
\( \LARGE \Delta = b^2 – 4ac \)
\( \LARGE \Delta = -8<0 \)
ریشه ندارد
مثال ۱۵ : \( \Large y=-2x^2+4x-7 \) را تعیین علامت کنید.
\( \LARGE -2x^2 + 4x -7 =0 \)
\( \LARGE \Delta = b^2 – 4ac \)
\( \LARGE \Delta =16-28=-12<0 \)
ریشه ندارد
نکته ۴ تعیین علامت عبارت های جبری : حال اگر در یک عبارت هم درجه اول و هم درجه دوم داشته باشیم:
- ابتدا ریشه‌های همگی را پیدا کرده در جدول نوشته.
- هر کدام را به روش خودش تعیین علامت میکنیم
- در نهایت علامت ستون‌ها را در هم ضرب میکنیم.
مثال ۱۶ تعیین علامت عبارت های جبری: \( \Huge y=\frac{(x^2-5x-6)\left| x-2 \right|}{(3-4x)^3} \) را تعیین علامت کنید.
(1
\( \LARGE x^2-5x-6 =0 \)
\( \LARGE x_1=6,x_2=-1 \)
(2
\( \LARGE x-2 =0 \)
\( \LARGE x=2 \)
(3
\( \LARGE 3-4x =0 \)
\( \LARGE x=\frac{3}{4} \)
ریشه مخرج
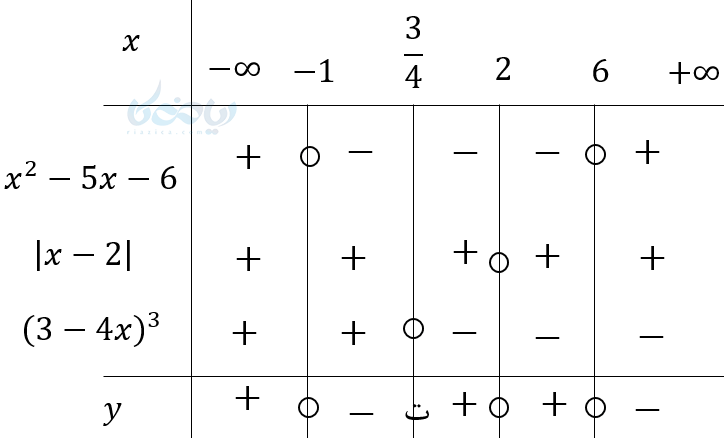
یک ویدیو آموزشی از حل تمرین کتاب آموزش ریاضی دهم
زنگ آخر کلاس تعیین علامت عبارت ها
یکی از کاربردهای تعیین علامت عبارت های جبری در آموزش ریاضی دهم حل نامعادله است که در بخش نامعادله آن را باهم یاد گرفتیم. همچنین این مفهوم مهم را با بیش از ۱۵ مثال و نمودارهای گوناگون باهم بررسی کردیم.
در صورتیکه که هر گونه سوالی از این بخش داشتید می‌توانید آن را در بخش دیدگاه‌ها که در زیر همین قسمت قرار دارد برای ما بنویسید. گروه آموزشی ریاضیکا به سوال‌هایتان پاسخ می‌دهد.
ما رو حتما در آپارات دنبال کنید تا ویدیوهای بیشتری رو از ما ببینید.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی دهم به شما پیشنهاد می‌دهیم:
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- آموزش احتمال دهم – کامل‌ترین و جامع‌ترین آموزش 🔣❓
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
بسیار عالی
خیلی خیلی خوب بود
سپاس??
ضمن عرض سلام و احترام
خوشحالیم که براتون مفید بوده
و سپاسگزاریم بابت انرژی مثبت شما
موفق و پیروز باشید
عالی بود ممنون??
با سلام وعرض ادب
خوشحالیم که مفید واقع شده
هدف از تعیین علامت چند جمله ای ها چیه ؟
با سلام دوست عزیز
کاربردهای متعددی داره مثلا وقتی یه عبارت جبری داخل قدر مطلق هست ومیخواهیم اون رو از قدر مطلق بیرون بیاریم اول اون رو تعیین علامت میکنیم وبا توجه به علامتش اون رو از قدر مطلق بیرون میاریم مثبت باشه خودش میاد بیرون منفی باشه قرینه اش یا حل نامعادلات درجه دوم وکسری وغیره با تعیین علامت حل میشه
بسیار عالی بود ، استفاده کردم از آموزش عالی تون.سپاس
با سلام وادب
خدا رو شکر مفید بوده
🖤🖤🖤💛
very very gooooood
You are welcomeeeeeeeeeeeeeeee 🙂
اومدم مرور کنم کلی چیز جدید یاد گرفتم. دمتون گرم!
ضمن عرض سلام
بسیار باعث خوشحالیست که این نوشتار برای شما مفید بوده
موفق و پیروز باشید
ممنون خیلی عالی و روان توضیح دادید خدا خیرتون بده
سلام ممنون از توجهتون.
با معرفی ما به دوستانتون ما را در پیشرفت سایت کمک کنید.
سلام خسته نباشید
جواب سوال اصلیمو (چه زمانی باید عبارت را تعیین علامت کرد؟)رو نگرفتم.ولی متن جامعی بود.
سلام وقت به خیر
این پست مربوط به پایه دهم است که ما در این پست روش‌های تعیین علامت را بیان کرده‌ایم و در همین پست دیدید برای حل نامعادلات کسری و نامعادلات درجه دو و نامعادلات قدرمطلقی باید ابتدا عبارت را تعیین علامت کنیم.
این پست https://riazica.com/solving-inequalities/ را هم مطالعه کنید.
سلام
من این سوال واسم پیش اومد که اگه دو عبارت مثل هم در صورت مخرج وجود داشته باشه که باهم ساده بشن اونموقع علامتش چجوری میشه یا اصلا ما باید اونرو توی جدول بنویسیم ؟
یا مثلا اگه در صورت همان عبارت توان سه داشت و در مخرج توان یک اونموقع چی میشه ؟؟
سلام اگر عاملی که در صورت و مخرج ساده میشود دارای متغیر باشد باید آن را همان گونه تعیین علامت کنیم اما اگر عدد باشد می‌توانیم ساده کنیم بعد تعیین علامت کنیم.
جواب سوال دومتون:
اگر عبارتی توان فرد داشته باشد بدون در نظرگرفتن توان آن را تعیین علامت میکنیم و توان تاثیری بر تعیین علامتش ندارد.
سلام
خیلی بابت توضیخات دقیق تون ازتون ممنونم واقعا خیلی عالی بود.
سلام ممنون از شما بایت انرژی فوق العاده تون .
سلام
خیلی بابت توضیخات دقیق تون ازتون ممنونم واقعا خیلی عالی بود.
سلام مرسی ازتون واقعا انرژی گرفتیم.
سلام تعیین علامت « منفی x به توان ۷ » به چه صورته؟
با سلام وعرض ادب
وقتی توان فرد میباشد بدون در نظر گرفتن توان پایه را تعیین علامت میکنیم مثل مثال ۶
خیلی عالی بود وقعا ممنونم بابت توضیحات جامعتون
با سلام وعرض ادب واحترام
ممنون از انرژی مثبتتون
سلام جناب مثال ۱۶ حس کردم تو ریشه گیری صورت ایرادی وجود داره باید x1وx2صورت به ترتیب ۲ و ۳ میشدن ولی شما زدین x1=6و x2=-1این اشتباه نیست لطفا توضیح دهید ممنون از مطالب گرانبهایتان???
سلاموعرض ادب
دوست عزیز دو عدد که ضرب انها ۶- وجمع آنها ۵- شود ۶- و۱ میباشد که بعد حل معادله به ۶و-۱میرسیم وعلامتها هم چک شد درست هست
سلام ببخشید مثال 16 و8 چگونه تعیین علامت شده اند؟
واقعاااااا عالییییی
سلا ووقت به خیر
ممنون از نظر لطف شما
سلام جناب مثال ۱۶ حس کردم تو ریشه گیری صورت ایرادی وجود داره باید x1وx2صورت به ترتیب ۲ و ۳ میشدن ولی شما زدین x1=6و x2=-1این اشتباه نیست و تو علامت گذازی صورت کسر هم اشتباهی رخ داده لطفا توضیح دهید که اشتباه میکنم یا درست میگم ممنون از مطالب گراتبهایتان???
با سلام
پاسخ داده شد
سجلام من امتحان دارم ولی خیلی سخته کمک میخام
چگونه معادله ی درجه اول همواره مثبت یا منفی است
با سلام واحترام
اگرداخل قدر مطلق باشد همواره مثبت است یا به توان عدد زوج رسیده باشد در پست مثالهای مختلف آورده شده
سلام میشه بگید با ی مثال که چرا عبارت همواره مثبت در تعیین علامت تاثیر نداره؟
سلام میشه بگید چرا عبارت های مثبت در تعیین علامت بی تاثیر هستند؟
با سلام وعرض ادب
چون مثبت در مثبت میشود مثبت و مثبت در منفی هم میشود منفی یعنی اگر یک عبرت چه در عبارت مثبت چه در عبارت منفی ضرب شود روی علامت ها تاثیر ندارد اینجا مثال زدن ممکن نیست
سلام در جدول تعیین علامت مثال 8 انگار اشتباه پیش اومد. مثبت در منفی شده مثبت.که باید می شد منفی .
اگر من اشتباه می کنم .لطفا دلیلش را به من توضیح دهید با تشکر.
سلام وعرض احترام
درست میفرمایید تصحیح شد اشتباه تایپی بود
ممنون
با سلام و تشکر
در مثال( ۴. دو عبارت درجه اول که در هم ضرب یا به هم تقسیم شده‌اند.) به نظر در جدول تعیین علامت اشتباه تایپی رخ داده است.
با سلام
در مثال ۴ که یه عبارت بهتوان دو رسیده بنابراین به ازای همه مقادیر جز ریشه مثبت میشود
سلام خسته نباشید. همیشه زمانی که میخوایم معادله قدرمطلقی رو برابر صفر بزاریم قدر مطلق رو برمیداریم و خیلی معمولی ایکس رو حساب میکنیم؟ یا استثنائی هم داره؟
با سلام
خیر دوست عزیز قدر مطلق رو بر میداریم وطرف دوم رو یه با با علامت مثبت ویه با با علامت منفی حل میکنیم
سلام. ببخشید اگه عبارت درجه ۲ با ضریب مثبت تو مخرج باشه و عبارت درجه ۱ با ضریب منفی تو صورت کسر بعدی ، و فقط یک ریشه a داشته باشه ، قبل a میشه موافق ضریب x^2 یا مخالفش؟
با سلام
من منظور شما رو درست متوجه نشدماگه اون ریشه مال معادله درجه دوم باشه در این صورت چون یه ریشه داره مخرج همواره موافق ضریب ایکس هست که در اینجامثبته
سلام برای عبارات فاکتوریل دار باید چه کار کرد؟
با سلام وادب
اونها رو‌نمیدن که تعیین علامت کنید
🖤🖤🖤💛
سلام. خیلی خوب بود ولی یه سوال.. چه وقتایی باید توی ردیف اخر بگیم تعریف نشده؟؟
با سلام
عددهایی که ریشه مخرج هستن تعریف نشده میباشن
سلام روزتون بخیر
ببخشید چه زمانی در معادله نیاز نیست جدول تعیین علامت بکشیم؟؟؟
با سلام
وقتی نا معادله درجه اول ساده هست میشه بدون تعیین علامت حلش کرد
عالی و فوق العاده بود ???
با اینکه این مبحثو از درسنامه کاملی مطالعه کرده بودم اما برام مفید نبود و بزرگترین مشکل پایه ایم ?
ولی الان کامل یاد گرفتم دستتون درد نکنه ?عالی هستید
موفق باشید همیشه ❤
با سلام
خدا رو شکر
سلام ممنون خیلی مختصر ومفید ??
سلام دوست عزیز
ممنون از نظر شما هدف ما هم همین است
هدف از تعیین علامت چند جمله ای ها چیه ؟
با سلام
در مبحثی مثل حل معادلات قدر مطلقی و حد گیری وغیره کاربرد زیادی داره
سلام در مورد سوال ۱۶ اولا من از طریق دلتا حل میکنم جواب ۲و۳ میاد دوما به روش شما حل میکنم جواب ۶- و ۱ میاد ولی شما میگید ۱- و ۶ که این اشتباه لطفا بگید چرا جواب ها از طریق دلتا و روش شما با هم فرق میکنه
سلام دوست عزیز
از هر روشی برید جواب همین میشه اگه از راه تجزیه برید دو عددی که ضربشون منفی شش وجمعشون منفی پنج بشه منفی شش ومثبت یک هست که وقتی مساوی صفر قرار بدیم همین جوابها بدست میاد برید حتما پست حل معادله درجه دوم رو حتما بخونید که ما در همین بخش قرار دادیم
سلام عالی توضیح دادین خدا خیرتون بده ممنووون
با سلام وادب ممنون از پیام دلگرم کننده شما
ممنون بابت این توضیح جامع و دقیقتون.خیلی زودتر از ویدیو های آموزشی تعیین علامت رو به دانش آموز آموزش میدید
ممنون بابت روحیه ای که به مابرای ادامه کار میدهید
سلام
قسمت یک مثال برای درک بهتر تعیین علامت اون آخرش قبل جدول باید مینوشتید y منفی است لطفاً اصلاح کنید
سلام ببخشید مثال 16 و8 چگونه تعیین علامت شدند؟
با سلام و ادب
هر عبارتراجدا گانه نعیین علامتکرده سپس علامتها رادرهم ضرب میکنیم
💛🖤🖤🖤🖤
سلام وقتتون بخیر
این عبارت را چگونه باید تعیین علامت کنیم:
قدر مطلق باز 2x+1 قدر مطلق بسته، منهای قدر مطلق باز x-1 قدر مطلق بسته.
(x-1)-(2x+1)=P
P=(2x+1)-(x-1)
البته من بجای قدرمطلق از پرانتز استفاده کردم.
خیلی ممنون میشم برامون حل کنید.
مرسی
با سلام
ابتدا ریشه عبارتهای داخل قدرمطلق رو به دست آورید سپس در یک جدول ریشه ها رو نوشته وهر عبارت رو تعیین علامت کنید سپس عبارت اصلی رو با توجه به علامت داخل جدول بدون قدر مطلق بنویسید که سه حالت میشه یکی کوچیکتر از منفی یک دوم یکی بین منفی یک دوم ویک وبعدی بیشتر از یک
واااقعاااا عالی بود ممنونممم❤️😍 خیلی خوب یادش گرفتم منی که دوازدهم هستم و هنوز توش مشکل داشتم
با سلام خدا رو شکر که برای شما مفید واقع شده