آموزش ریاضی پایه دهم
آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
مثلثات چیست؟ شاخهای از ریاضیات است که به بررسی روابط بین زوایا و اضلاع یک مثلث میپردازد. یکی از مهمترین اهداف این شاخه اندازهگیری فاصلهها به صورت غیرمستقیم است. مثلاً چگونه بتوانیم بلندای یک ساختمان یا یک کوه و یا عرض یک رودخانه را به راحتی و بدون اندازهگیری محاسبه کنیم.آموزش مثلثات در شاخههای زیر کاربرد فراوان دارد:
- علوم مهندسی
- فیزیک
- نقشه برداری
- دریانوردی
- نجوم
- …
تاریخچه مثلثات
که اولین لوح های پیدا شده در مورد موضوع مثلثات به سه هزار سال قبل از میلاد میرسد. همین مسئله نشان میدهد که دانشمندانی که در قرنها پیش زندگی میکردند، به این علم دست یافته بودند. مادر علم مثلثات را میتوان هندسه دانست. چراکه این شاخه از علوم ریاضیات از درون هندسه درآمده و صدها ریاضیدانان ایرانی در توسعهٔ آن نقش داشتهاند.
بررسیهای اخترشناسی در بابل قدیم و یونان، ریاضیدانان را بهسمت موضوعهایی کشاند که یافتههای آنان را میتوان مقدمهای بر مثلثات دانست. در میان این بزرگان میتوان به دانشمندانی از ایران و یونان اشاره کرد. ارشمیدس و ابوالوفای زنجانی تحقیقات و نوشتههای گستردهای در زمینه مثلثات از خود باقی گذاشتهاند.
اما گام اصلی را خواجه نصیرالدین طوسی برداشت. نقش طوسی را در مثلثات باید شبیه نقشه اقلیدس در هندسه دانست. زیرا او توانست مجموعهٔ آنچه را که پیش از او وجود داشت به صورت دانشی مستقل و منظم در آورد. تألیف او در کتابی به نام کشف القناع فی اسرار شکل القطاع قرار دارد که در واقع نخستین کتاب دربارهٔ علم و آموزش مثلثات است. ترجمهٔ کتاب خواجه نصرالدین طوسی، در سال 1891 به زبان فرانسوی انجام گرفت و تا مدتها به عنوان کتاب درسی، مورد استفادهٔ دانشمندان در اروپای غربی بود.
جالب است بدانید نامهای انتخاب شده برای نسبتهای مثلثاتی توسط ریاضیدانان ایرانی صورت گرفته است. این نامها مدتها بعد به زبانهای عربی و سپس به فرانسه ترجمه شده و به شکل امروزی در آمدهاند. جدول این اسامی در زیر آمده است:
| نام قدیم در فارسی | نام عربی | نام فرانسه | نماد فعلی |
|---|---|---|---|
| گریبان | جَیب | سینوس | sin |
| گریبان پُر | جَیب تمام | کسینوس | cos |
| سایه | ظل – ظل معکوس | تانژانت | tan |
| سایه پر | ظل تمام – مستوی | کتانژانت | cot |
| برنده | قاطع، قطر ظل | سکانت | sec |
| برنده پُر | قاطع تمام | کسکانت | cosec |
آموزش نسبتهای مثلثاتی
همانطور که میدانیم، وقتی در دو مثلث زوایای برابر وجود داشته باشد آن دو مثلث مشابه هستند. در نتیجه نسبت اضلاع متناظر آنها باهم برابر است.

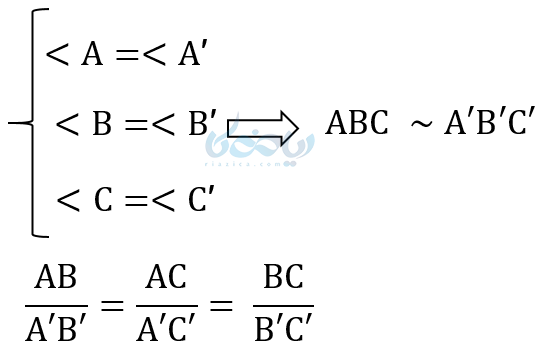
نکته مهم: اگر در دو مثلث قائم الزاویه، یک زاویه تند برابر داشته باشیم، دو مثلث متشابه هستند. در نتیجه نسبت اضلاعشان باهم برابر است. مثلاً در تمام مثلثهای قائم الزاویهای که یک زاویهٔ 30 درجه دارند، نسبت اضلاع باهم برابر است:
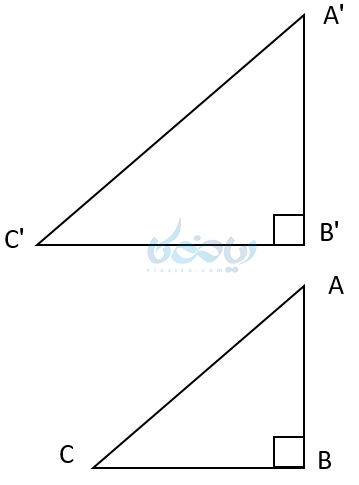
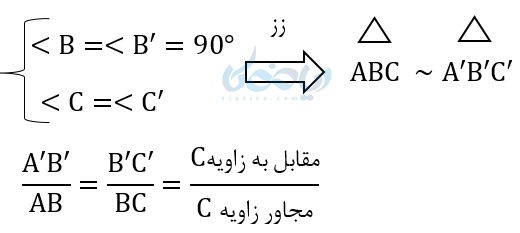
یک مثال دیگر برای فهم بهتر این بخش از آموزش مثلثات
مثال ۱: زاویه زیر را در نظر بگیرید:
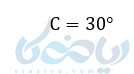
در تمام مثلثهای قائم الزاویه با زاویه 30 درجه، نسبت ضلع مقابل به زاویهٔ C،به ضلع مجاور به زاویهٔ C باهم برابر است. این مثال به راحتی برای شما قابل اندازهگیری است. برای این کار هم میتوانید با رسم دو مثلث قائم الزاویه با زاویه 30 درجه وبا اندازه اضلاع مختلف این موضوع را بررسی کنید وبا ماشین حساب صحت کارتان را ببینید .ریاضیدانان برای آسانی کار برای این نسبتها اسم گذاشتهاند و اکنون آنها را با نام نسبت های مثلثاتی میشناسیم که بخش مهمی در آموزش مثلثات هستند.
نسبتهای مثلثاتی :
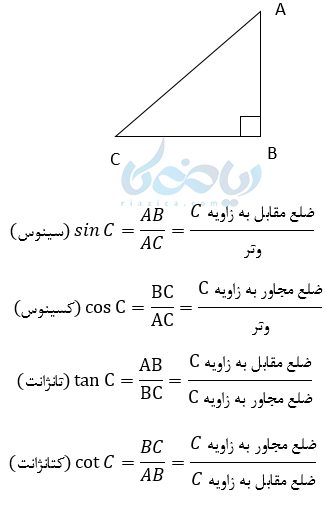
البته \( \Large sin , tan , cos \) نسبتهای مثلثاتی اصلی هستند که در ماشین حسابها نیز کلید آنها وجود دارد.
اگر در یک مثلث قائم الزاویه اندازه یک زاویه و یک ضلع از آن مثلث را داشته باشیم، میتوانیم بقیه ضلعها را بدست آوریم. برعکس این حالت نیز درست است. به این شکل که با داشتن اضلاع اندازه زاویهها را نیز میتوانید محاسبه کنید.
مثالی دیگر در آموزش نسبتهای مثلثاتی
مثال ۲: در مثلث قائم الزاویهٔ زیر نسبتهای مثلثاتی B را بدست آورید؟

نسبتهای مثلثاتی 30 و 60 و 45 درجه
شما با استفاده از ماشین حساب میتوانید هر نسبت مثلثاتی برای هر زاویهای را محاسبه کنید. اما در بین این زوایا، چند زاویه هستند که بسیار پرکاربرد و مهم بوده و بهتر است نسبتهای مثلثاتی آنها را همیشه به خاطر داشته باشید. نکته جالب اینجاست که با آموزش مثلثات میتوان با استفاده از یک مثلث متساوی الاضلاع و یک مربع به راحتی نسبتها 30 و60و45 درجه را بدون اندازهگیری و به طور دقیق بدست آوریم.
در ریاضی پایه یازدهم با استفاده از این زوایای پرکاربرد قادر خواهید بود که زوایای زیاد دیگری را از روی دایره مثلثاتی به راحتی محاسبه کنید. مانند: 120 و 150 و 210 و … . در ادامه با نسبتهای مثلثاتی این زوایای پرکاربرد آشنا میشویم.
نسبتهای مثلثاتی 30 و 60 درجه
در مبحث آموزش مثلثات، استفاده از مثلث برای پیدا کردن نسبت های مثلثاتی بسیار پرکاربرد است. برای پیدا کردن نسبت های مثلثاتی زوایای ۳۰ و ۶۰ درجه یک مثلث متساوی الاضلاع را با اندازه ضلع دلخواه در نظر میگیریم و یکی از ارتفاعهای آن را رسم میکنیم. ما میدانیم زاویههای مثلث متساوی الاضلاع 60 درجه است و میدانیم که در این مثلث ارتفاع، میانه و نیمساز هر ضلع در واقع یکی هستند. پس با رسم ارتفاعِ یکی از قاعدهها، دو مثلث قائم الزاویه داریم که یک زاویهٔ آنها 30 درجه میباشد. در نتیجه خواهیم داشت:

\( \Large \Delta AHC : \)
 \( \Large \Delta AHC : \)
\( \Large \Delta AHC : \)

نکته جالب این است که همانطور که میبینید زاویه 30 و 60 درجه متمم یکدیگرند. یعنی مجموع آنها 90 درجه است. پس:
\( \Large sin 60 = cos 30 \)
\( \Large cos 30 = sin 60 \)
\( \Large tan 30 = cot 60 \)
\( \Large cot 30 = tan 60 \)
این مطلب در مورد تمام زوایایی که با هم متمم هستند صدق میکند. پس به طور کلی داریم:
\( \Large sin (90 – \theta) = cos \theta \)
\( \Large tan (90 – \theta) = cot \theta \)
مثال ۳:
\( \Large sin 10 = cos 80 \)
\( \Large sin 25 = cos 65 \)
\( \Large tan 20 = cot 70 \)
نسبتهای مثلثاتی 45 درجه
نسبت های مثلثاتی زاویه ۴۵ درجه کاربرد زیادی در مبحث آموزش مثلثات و نسبتهای مثلثاتی دارد. برای محاسبه نسبتهای مثلثاتی 45 درجه از یک مربع با طول ضلع دلخواه استفاده کرده و یکی از قطرهای آن را رسم میکنیم. قطر مربع نیمساز زوایای آن نیز میباشد. پس دو مثلث قائم الزاویه متساوی الساقین داریم زوایای آنها 45 درجه است. در نتیجه داریم:
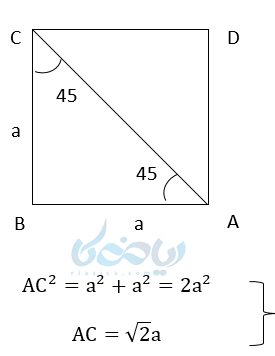

جدول نسبتهای مثلثاتی برای زوایای 30 و 45 و 60 درجه
| 45 | 60 | 30 | |
|---|---|---|---|
| \( \Large \frac{\sqrt2}{2} \) | \( \Large \frac{\sqrt3}{2} \) | \( \Large \frac{1}{2} \) | sin |
| \( \Large \frac{\sqrt2}{2} \) | \( \Large \frac{1}{2} \) | \( \Large \frac{\sqrt3}{2} \) | cos |
| 1 | \( \Large \sqrt3 \) | \( \Large \frac{\sqrt3}{3} \) | tan |
| 1 | \( \Large \frac{\sqrt3}{3} \) | \( \Large \sqrt3 \) | cot |
ویدیو آموزش نسبت های مثلثانی و نسبت هایش
در این ویدیو مطالب بالا کامل وروان توضیح داده شده است.
میخوای بیشتر در مورد نسبتهای مثلثات آموزش ببینی؟
تمرین: در مثلث زیر محیط و مساحت را محاسبه کنید.
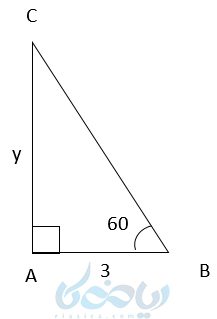
برای آموزش مطالب بیشتر در مورد مثلثات به پستهای دایره مثلثاتی و محاسبه مساحت مثلث بدون داشتن ارتفاع و روابط بین نسبتهای مثلثاتی مراجع کنید
این تمرین را حل کنید تا میزان یادگیری خود را از آموزش مثلثات بسنجید. در ادامه میتوانید پاسخ خود را در بخش دیدگاهها در پایین همین صفحه بنویسید. ما در ریاضیکا میخواهیم اشکالات شما را برطرف کنیم و به سوالاتتان پاسخ دهیم.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!





سلام.
محیطش میشه 12 رادیکال 3
مساحتش میشه 9 رادیکال 3
سلام دوست عزیز
ممنون از اینکه مسئله را حل کردید.
محیط : ۹ + ۳رادیکال۳
مساحت : ۴.۵ رادیکال ۳
موفق باشید.
سلام دوست گرامی قیمت هاتون فضایی هستش
سلام و احترام
پکیجی که در این پست مشاهده میکنید شامل ۱۱ ساعت ویدیو هست که حاصل ۳۰ سال تجربه تدریس توسط معلم نمونه استان تهران هست. اگر کل این مباحث را بخواهید با یک معلم خصوصی که حداقل ۱۰ سال سابقه تدریس دارد داشته باشید، باید مبلغی بالغ بر ۴ میلیون تومان هزینه کنید.
این ۳۵ قسمت کل ریاضی دهم رو شامل میشه و آموزش میده؟
با سلام وروز به خیر
بله دوست عزیز تمام درس به درس کتاب ریاضی تدریس شده به زبانی ساده وشیوا به صورت ویدیویی هم یک پکیج آموزش داریم که کل این سی وپنج قسمت تدریس شده
سلام میشه افزایش و کاهش نسبت های مثلثاتی روی دایره مثلثاتی رو نشون بدید