آموزش ریاضی پایه دهم
تابع خطی به سادگی یک خط مستقیم 📈
اسفند
در این نوشتار از آموزش‌های ریاضی دهم می‌خواهیم باهم با چند نوع تابع از جمله تابع خطی آشنا شویم و در مورد دامنه و برد نمودار آن‌ها صحبت کنیم. توابعی که در بخش تابع کتاب ریاضی دهم وجود دارند عبارتند از:
- توابع خطی
- تابع چندجمله‌ای
- تابع گویا
- تابع همانی
- تابع ثابت
- تابع قدرمطلق
- تابع درجه دوم
- تابع نمایی و لگاریتمی
- تابع مثلثاتی
- تابع رادیکالی
تابع خطی
معادلهٔ خط \( \Large y=2x-1 \) را در نظر بگیرید. اگر به \( \Large x \) مقادیر دلخواه بدهیم و همراه مقادیر \( \Large y \) آن‌ها را در یک جدول بنویسیم، داریم:
| 1 | ۰ | -۱ | x |
|---|---|---|---|
| 1 | -1 | -3 | y |
همانطور که مشاهده می‌کنید این جدول بیانگر یک تابع است. چون به ازای هر \( \Large x \) دقیقاً یک \( \Large y \) داریم و اگر آن‌ها را به صورت زوج مرتب بنویسیم، خواهیم داشت:
\( \LARGE f=\{(-1,-3),(0,-1),(1,1)…\} \)
پس نتیجه می‌گیریم که این خط یک تابع را نشان می‌دهد و نمودار آن به صورت زیر خواهد بود.
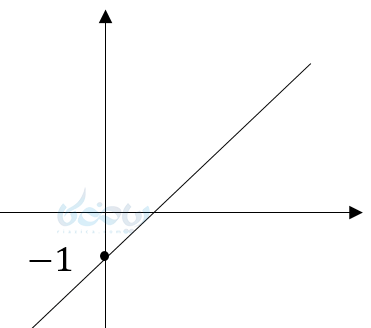
یک مثال از ظاهر نمودار تابع خطی
\( \LARGE D_f = \mathbb{R} \)
\( \LARGE R_f = \mathbb{R} \)
اگر به جدول دقت کنید طول‌ها و عرضها با یک مقدار ثابت تغییر می‌کند. یعنی وقتی طول‌ها یکی یکی اضافه شود، \( \Large y \)ها (سه تا سه تا) اضافه می‌شود. این خاصیت تمام توابع خطی است که نقاط همه در یک امتداد هستند و برای همین نمودار آن‌ها یک خط راست است.
نمودار کلی تابع خطی به صورت زیر است:
ظاهر کلی نمودار تابع خطی
تعریف تابع خطی
هر تابعی که بتوان آن را به شکل\( \Large y=ax+b \) نمایش داده یک تابع خطی نامیده می‌شود.
مفهوم شیب در نمودار خط و فرمول آن
مثال ۱: آیا جدول زیر نمایش یک تابع است؟ اگر هست چه نوع تابعی و چرا؟
حل ۱:
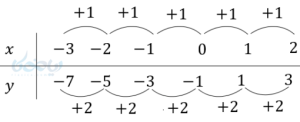
بله این جدول نمایش یک تابع است. چون به ازای هر \( \Large x \) فقط یک \( \Large y \) داریم. پس از نوع تابع خطی است. به این علت که مقادیر \( \Large x,y \) با یک مقدار ثابت تغییر می‌کنند.
حال اگر بخواهیم معادله این خط را بنویسیم همانطورکه قبلاً آموخته‌ایم، ابتدا شیب خط را با استفاده از دو نقطه این خط بدست می‌آوریم.
\( \LARGE m=\frac{y_2-y_1}{x_2-x_1} \)
\( \LARGE m=\frac{-1-(-3)}{0-(-1)}=\frac{2}{+1} \)
\( \LARGE m=2 \)
\( \LARGE y=ax+b \)
\( \LARGE \rightarrow (0,1),a=2 \)
\( \LARGE 1=0\times (2)+b \)
\( \LARGE b=1 \)
\( \LARGE y=2x+1 \)
نکته ۱: به معادله یک تابع ضابطه تابع یا نمایش جبری تابع نیز گفته می‌شود.
نکته مهم ۲: تا کنون یاد گرفتیم که هر تابع را به چهارشکل (زوج مرتب، نمودار ون، جدول و نمودار مختصاتی) می‌توان نمایش داد اما نمایش دیگر تابع ضابطه یا همان معادله تابع است. البته این نوع نمایش برای همه توابع امکان پذیر نیست و برای بعضی از توابع نمی‌توان معادله نوشت.
نکته ۳: خط \( \Large x=a \) جزو توابع نیست(خطهایی که موازی محور عرضها هستند).
نکته ۴: بزرگترین دامنه ممکن و برد تمام توابع خطی \( \Large \mathbb{R} \) می‌باشد به جز خط‌ها \( \Large y=b \) که بردشان فقط شامل \( \Large b \) است.
نکته ۵: در عکس زیر حالت‌های متفاوت علامت شیب خط را مشاهده می‌کنیم.
مثال ۲: نمودار معادله خط \( \Large y=2x+3 \) را رسم کنید.
حل ۲:
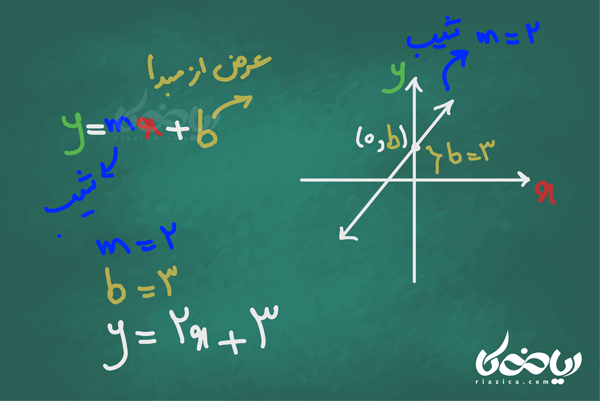
حل مثال ۲ روی تخته سیاه ریاضیکا 🙂
آخر کلاس آموزش تابع خطی
در این آموزش از تابع خطی سعی کردیم همراه با تصاویر و فرمول‌های مفهومی این آموزش مهم از ریاضی دهم را باهم یاد بگیریم. در صورتیکه هرگونه سوالی از این مبحث داشتید، در بخش دیدگاه‌ها در پایین همین نوشتار سوال خود را بپرسید. ما در ریاضیکا به سوالات شما پاسخ می‌دهیم.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی دهم به شما پیشنهاد می‌دهیم:
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!🙂
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 🙂
- آموزش الگو و دنباله به راحتی آب خوردن 🌊💡!
- آموزش دنباله حسابی 💡 – از همیشه سادهتر😉
- آموزش دنباله هندسی 📈👌 – دنباله را اینجا دنبال کنید!
- آموزش نسبت‌های مثلثاتی: توضیحات کامل 💎همراه با تصویر
- محاسبه مساحت بدون داشتن ارتفاع!🔮 – چیزی شبیه معجزه
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- روابط بین نسبت های مثلثاتی : 💎⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 💪 !
- صفر تا صد توان های گویا 📘 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 🔥
- تجزیه عبارت های جبری به 4 روش مختلف 📚
- عبارت های گویا 📜 به سادگی آب خوردن
- گویا کردن مخرج گنگ 🤔🔋 مثل آب خوردن!
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن💪🔮
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش حل نامعادله همراه با رسم نمودار و مثال‌های متنوع📈
- تابع چیست ؟ تمام آنچه باید بدانید.📍
- دامنه و برد تابع به زبان عکس‌ها 😍
- تابع خطی به سادگی یک خط مستقیم 📈
- تابع چند جمله ای به زبان ساده 📝
- تابع همانی – همان آموزشی که دنبالش بودید 👌
- تابع ثابت را در حافظه خود ثابت کنید 📝 !
- رسم نمودار تابع قدر مطلق به زبان شکلها 📐💎
- رسم سهمی با روش انتقال به سادگی آب خوردن!🌊
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 💪
- تابع گویا – گویاتر از همیشه یاد بگیر 📜
- اصل شمارش ، بدون شمردن 😮
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- آموزش جایگشت یا جابجایی 📚 مفهومی‌ترین آموزش
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️!
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 👀
- آموزش آمار ریاضی دهم 📉 تنها آموزش آمار که باید بخوانید!
ممنون واقعا بابت تدریس عالی تون🌷
با سلام وعرض ادب
ممنون از توجه شما
موفق باشید
خواهش نظر لطفتون است
ضابطه تابع چیه؟
با سلام
همون معادله تابع یا اسم دیگه آن نمایش جبری است مثلا در تابع خطی y=2x+1 به این معادلهضابطه تابع هم می گویند
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
بسیار عالی👌
با سلام وعرض ادب
ممنون از انرژی شما
خواهش
اونجا y2 منهای y1 کلا شیب خط چطور محاسبه شده اصلا منفی ۴ نداشت
با سلام وعرض احترام
ممنون از توجه شما اصلاح شد
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
ممنونم از مباحث خوبتون
خسته نباشید
با تشکر حجت هستم
با سلام واحترام
خوشحالیم که مفید بوده براتون
عالی بود ممنون
ممنون از شما
با سلام و احترام
تشکر از تدریستون
کدام خطوط درصفحه مختصات نمودار یک تابع خطی نیست؟چرا؟
با سلام
خطهایی که موازی محور عرضها هست چون تمام نقاط واقع بر آن دارای طولهای میاوی هستند
راس سهمی رو توضیح بده!
آقا نیمار علیک سلام این پست رو بخون https://riazica.com/parabola/
سهمی رو توضیح بده
علیک سلام دوست عزیز
برو این پست رو بخون https://riazica.com/parabola/
سلام
آیا تدریس خصوصی هم دارید؟
با سلام وادب
بله
سلام دوست عزیز
بله به صورت آنلاین در گوگل میت برای هماهنگی با شماره ۰۹۱۲۸۱۴۸۹۷۵ تماس بگیرید