آموزش ریاضی پایه دهم
متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
دی
موضوع درس دوم از فصل اول کتاب ریاضی پایه دهم متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه است. این بخش از کتاب، مبحثی مهم است، چرا که در بخش احتمالات نیز در آینده از این مبحث استفاده خواهد شد.
مجموعه مرجع
در بحث متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه در ریاضیات، زمانی که در مورد یک مجموعه خاص و زیرمجموعه‌های آن صحبت میکنیم، به مجموعه مورد نظر مجموعه، مادر یا جهانی یا به قول کتاب مجموعه مرجع می گویند. مجموعه مرجع را با U یا در بعضی از کتاب‌های درسی با M نمایش می‌دهند.
متمم یک مجموعه
حال اگر مجموعه A بخشی را از این مجموعه مرجع در نظر بگیریم، آنگاه ‘A یا متمم A مجموعه‌ای می‌باشد که عضوهایش عضو A نباشند. در این حالت به زبان ریاضی می‌نویسیم:
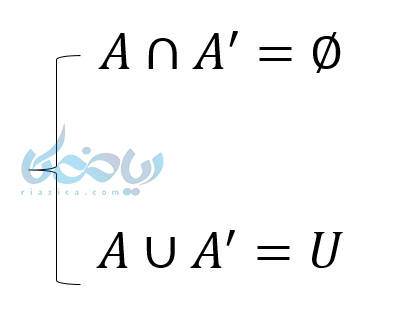
پس اشتراک یک مجموعه با متممش تهی و اجتماع آن با متممش مجموعه مرجع می باشد.اگر بخواهیم به زبان نمودار این مسئله را بیان کنیم خواهیم داشت:
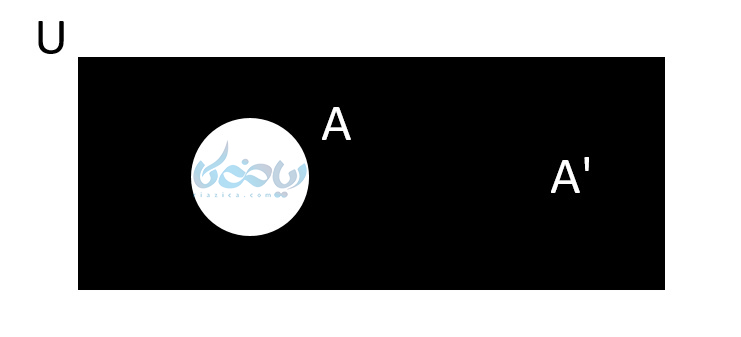
چند مثال از متمم یک مجموعه
اجازه بدهید با حل یک مثال، این مورد را برای شما بهتر توضیح دهیم.
مثال ۱: اگر مجموعه‌ی Z را مجموعه مرجع در نظر بگیریم و مجموعه A به شکل زیر تعریف بشود، مجموعه متمم آن را بنویسید.
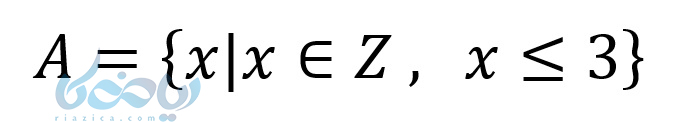
حل: با کمک متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه می‌نویسیم:
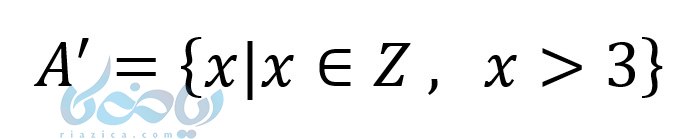
مثال ۲: اگر مجموعه‌ی مرجع R باشد و (A=[-1,22 ، آنگاه متمم آن را بنویسید.
حل: با کمک متمم یک مجموعه خواهیم داشت:
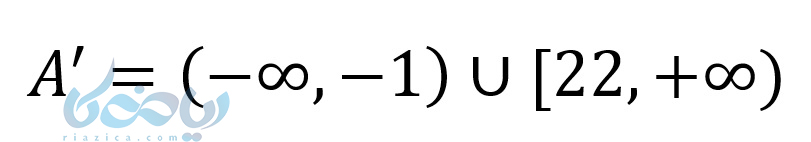
قوانین مجموعه مرجع و متمم یک مجموعه :
در بحث متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه قوانینی برقرار هستند که دانستن آنها برای دانش‌آموزان ریاضی پایه دهم بسیار مهم است. این قوانین عبارتند از:
(1
\( \Large U’ = \emptyset \)
(2
\( \Large \emptyset’ =U \)
(3
\( \Large A \cup A’ = U \)
(4
\( \Large A \cap A’ = \emptyset \)
(5
\( \Large (A \cup B)’ = A’ \cap B’ \)
(6
\( \Large (A \cap B)’ = A’ \cup B’ \)
(7
\( \Large A – B = A \cap B’ \)
(8
\( \Large A – B = A – (A \cap B) \)
(9
\( \Large (A’)’ = A \)
(10
\( \Large A \cup U = U \)
(11
\( \Large A \cap U = A \)
(12
\( \Large A’ = U – A \)
(13
\( \Large A = U – A’ \)
نکته ۱: 5 و 6 به قوانین دمورگان معروف هستند.
دو مجموعه‌ی جدا از هم
به دو مجموعه‌ای که هیچ عضو مشترکی ندارند، دو مجموعه جدا از هم می‌گویند. یعنی:
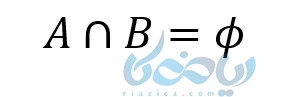
دقت کنید که لزوماً دو مجموعه‌ی جدا از هم متمم نمی‌باشند. چون اجتماع تمام آنها مجموعه‌ی مرجع نمی‌شود. پس دو مجموعه‌ی متمم جدا از یکدیگر هستند. ولی عکس این مطلب لزوماً درست نیست.
تعداد عضو های اجتماع
همانطور که در سال‌های قبل دیدیم وقتی تعداد عضوهای یک مجموعه متناهی است، مانند مجموعه‌ی A، تعداد عضوهای آن را با \( \Large n(A) \) نمایش می‌دهیم.
حال می‌خواهیم در مورد تعداد عضوهای اجتماع دو مجموعه صحبت کرده و چند مسئله‌ی مهم در این‌باره را مطرح کنیم.
تعداد عضوهای اجتماع دو مجموعه برابر است با مجموع عضوهای دو مجموعه، منهای تعداد عضوهای مشترک آنها. یعنی:
\( \Large n(A \cup B) \)
\( \Large =n(A)+n(B)-n(A \cap B) \)
نکته ۲: تمام قوانین بالا که در مورد مجموعه مرجع و متمم گفته شد درمورد تعداد اعضایشان نیز برقرار است.
(1
\( \Large n(U’) = n(\emptyset) \)
(2
\( \Large n(\emptyset’) =n(U) \)
(3
\( \Large n(A \cup A’) = n(U) \)
(4
\( \Large n(A \cap A’) = n(\emptyset) \)
(5
\( \Large n((A \cup B)’ )= n(A’ \cap B’) \)
(6
\( \Large n((A \cap B)’ ) = n(A’ \cup B’) \)
(7
\( \Large n(A – B) = n(A \cap B’) \)
(8
\( \Large n(A – B) = n(A) – n(A \cap B)) \)
(9
\( \Large n((A’)’) = n(A) \)
(10
\( \Large n(A \cup U) = n(U) \)
(11
\( \Large n(A \cap U) = n(A) \)
(12
\( \Large n(A’) = n( U – A) \)
(13
\( \Large n(A) = n(U – A’) \)
چند مثال از تعداد عضوهای اجتماع دو مجموعه
مثال ۳: در یک مدرسه‌ی ۱۰۰ نفری اگر تیم والیبال مدرسه‌ی A از ۳۲ نفر تشکیل شده باشد و تعداد عضوهای تیم فوتبال مدرسه‌ی B، برابر ۲۸ نفر باشد و ۷ نفر در هر دو تیم عضو باشند، به سوالات زیر پاسخ دهید.
الف) تعداد افرادی که حداقل در یکی از دو تیم عضو هستند؟
ب) تعداد افرادی که فقط در تیم والیبال هستند؟
ج) تعداد افرادی که در هیچ کدام از دو تیم عضو نیستند؟
حل : با کمک متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه می‌نویسیم .
\( \Large n(U) = 100 \)
\( \Large n(A) = 32 \)
\( \Large n(B) = 28 \)
\( \Large n(A \cap B) = 7 \)
(الف
\( \Large n(A \cup B) \)
\( \Large =n(A)+n(B)-n(A \cap B) \)
\( \Large = 32 + 28 – 7 = 53 \)
(ب
\( \Large n(A – B) \)
\( \Large = n(A) – n(A \cap B) \)
\( \Large = 32 -7 = 25 \)
طبق اصل 8
(ج
\( \Large n(A’ \cap B’) \)
\( \Large = n(A \cup B)’ \)
\( \Large = n(U) – n(A \cup B) \)
\( \Large = 100 – 53 = 47 \)
طبق اصل 13 و 5
مثال ۴: اگر رابطه زیر برقرار باشد:
\( \Large n(U) = 100 \)
\( \Large n(A) = 60 \)
\( \Large n(B) = 40 \)
\( \Large n(A \cup B) = 80 \)
مطلوبست:
حل: با کمک متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه میتوان نوشت:
(الف
\( \Large n(A \cup B) \)
\( \Large = n(A) + n(B) – n(A \cap B) \)
\( \Large 80 = 40 + 60 – n(A \cap B) \)
\( \Large n(A \cap B) = 20 \)
(ب
\( \Large n(A’ \cap B) \)
\( \Large = n(B \cap A’) = n(B – A) \)
\( \Large = n(B) – n(A \cap B) \)
\( \Large = 40 – 20 = 20 \)
یعنی فقط B
(پ
\( \Large n(A \cap B’) \)
\( \Large = n(A – B) \)
\( \Large = n(A) – n(A \cap B) \)
\( \Large = 60 – 20 = 40 \)
یعنی فقط A
(ت
\( \Large n(A’ \cup B’) \)
\( \Large = n(A \cap B)’ \)
\( \Large = n(U) – n(A \cap B) \)
\( \Large = 100 – 20 = 80 \)
یعنی حداقل 80 نفر عضو هیچ تیمی نیستند
نکته ۳: وقتی مسئله می گوید حداقل یا لااقل یا دست کم چند نفر عضو هر دو مجموعه هستند یعنی تعداد اعضای اجتماع را می خواهد یا وقتی می‌گوید چند عضو A یا B یا هر دو هستند باز مفهوم اجتماع را می دهد.
آخر کلاس
قوانین مجموعه‌ها که در این آموزش برای شما دانش آموزان عزیز بیان شد، قوانین مهمی هستند که با به خاطر سپردن این روابط نکته‌ی دیگری برای شما باقی نمی‌ماندوهر مسئله در این زمینه را میتوانیدپاسخگو باشید.
اگر از هر بخش این آموزش سوالی دارید، می‌توانید سوال خود را در بخش نظرات همین صفحه مطرح کنید تا کارشناسان ما در ریاضیکا در سریع‌ترین زمان ممکن به شما پاسخ دهند.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی دهم به شما پیشنهاد می‌دهیم:
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
ببخشید میدونم سوالم سادست اما چرا تو مثبت و منفی بی نهایت علامت بازه بسته نیست؟؟؟
ضمن عرض سلام
مشکلی نیست دوست عزیز
اعداد مثبت و منفی بینهایت اعداد مشخصی نیستند که بخواهیم بازه را بسته قرار دهیم.
سلام چونکه بینهایت در واقع محدودیتی نداره که بخوایم توی ی عدد خاص محدودش کنیم چ شامل تمام اعداد میشه
سلام وقتتون بخیر
علامت اجتماع چی هست؟
سلام وقت به خیر
علامت اجتماع U است.
موفق باشید.
سلام ممنون از سایت خوبتون واقعا توضیاحات مفید و خوبی دادید متچکرم:)
با سلام وروز به خیر
ممنون از توجه شما ونظرات مفیدتون
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام. وقتتون بخیر. منظور از حداکثر در یکی از گروه ها باشند چیه؟
با سلام وعرض ادب
وقتی میگه حداکثر دونفر یعنی دونفر وکمتر وقتی میگه حداقل دونفر یعنی دونفر وبیشتر
خییییییییییییییلییییییییییی عالییییییی بود
ممنون ازتون
با سلام واحترام
ممنون از نظر لطف شما دوست عزیز
سلام وقت بخیر ۰ند تا سوال داشتم اول این که چطوری اشتراک دو عدد رو پیدا میکنیم؟ مثلا توی سوال اگه بپرسه که از ۳۵ نفر ۲۰ نفر فوتبال و ۲۳ نفر والیبال دوست دارند و ۳ نفر علاقیه ای بی هیچ یک ندارند . اشتراک ۲۰ و ۲۳ چگونه به دست میاد؟؟
با سلام وعرض ادب
دوست عزیز اشتراک بین دو مجموعه است نه عدد
شما ابتدا ۳-۳۵ میکنیمتا تعداد اعضای اجتماع دومجموعه بدست آید سپس تعداد اعضای دومجموعه یعنی ۲۰ و۲۳ را جمع میکنیم سپس از تعداد اعضای اجتماع کم کنید یعنی ۳۲-۴۳پس یازده نفر عضو هر دو‌تیم هستند یعنی تعداد اعضای اشتراک دومجموعه
سلام وقت بخیر
میشه قسمت”متمم دو مجموعه‌ی جدا از هم”رو برای من به صورت ساده تر توضیح بدین؟
خیلی ممنون میشم
با سلام
فرق دو مجموعه متمم و دومجموعه جدا از هم در این هست که هردو با اینکه اشتراکشون تهی هست وای اجتماع دومجموعه متمم همیسه میشود مجموعه مرجع ولی در مورد دو مجموعه جدا از هم اینطورنیست
یا این سوال رو اگر میشه جواب بدین
“اگردو مجموعه از هم جدا باشد،آیا میتوان گفت متمم های ان ها نیز از هم جدا هستند؟چرا؟”
ببخشید Aپریم اجتماعش با Bچی میشه
با سلام وادب
بسته به نوع مجموعه ها فرق میکنه
سلام . میدونم که متمم کیو میشود کیوپریم .
اما نمیدونم چطوری اعضای اون رو نشون بدم … آیا با بازه اینکار رو انجام بدم ؟ اگه اینطوره لطفا بگید چجوری نشون بدم??
با سلام وادب
این مجموعه که همون اعد اد گنگ یااصم هسترو نه میشه بااعضایشنشانداد نه با بازه فقطباید بشناسیدشون
سلام
دریک روزازبین ۱۰۴موردجرم گزارش شده ۷۰مورددرشب و۶۱مورددرحومه شهربوده است حداقل چندموردجرم درشب ودرون شهر گزارش شده است؟؟
میشه توضیح بدید
سلام وقتتون بخیر پاسخ ان آ اشتراکش با بی داخل پرانتز کامل و پریمش جوابش مگه نمیشه ان مرجع منهای ان آ اشتراکش با بی؟؟؟
با سلام دوست عزیز
اگه اجتماع باشه حرف شما درست بود ولی لشتراک چنین قانونی نداریم
سلام ببخشید من ی سوال الان دارم که بهم مجموعه A و B رو به صورت بازه داده اما مجموعه مرجع رو نداده و از من ‘A’_B رو میخواد
چیکار باید بکنم؟
سلام ببخشید من ی سوال الان دارم که بهم مجموعه A و B رو به صورت بازه داده اما مجموعه مرجع رو نداده و از من ‘A’_B رو میخواد
چیکار باید بکنم؟
با سلام دوست عزیز
در بازه ها مرجع مجموعه اعداد حقیقی محسوب میشه
سلام ببخشید خواستم بدونم متمتم N
برابرباR_N
با سلام وادب
بله
سلام فرمول هشت اشتباه
با سلام وادب
دوست عزیز درسته