آموزش ریاضی پایه دهم
تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
ما در درسنامه معرفی عبارتهای گویا نهم به طور کامل در مورد عبارتهای گویا توضیح دادیم اما یکی دیگر از توابع مهم که در آموزش ریاضی دهم باهم یاد خواهیم گرفت، آموزش تایع گویا است. این تابع از تقسیم نوابع چندجملهای به هم بدست میآیند که به طور جامع در در ادامه باهم در مورد آن صحبت خواهیم کرد.

تعریف تابع گویا
تابعی که از تقسیم دو تابع چند جملهای به هم تشکیل میشود را تابع گویا مینامند.
تابع گویا \( \LARGE f(x)=\frac{P(x)}{Q(x)} , Q \neq 0 \)
\( \LARGE f(x)=\frac{x}{x^3-x^2-1} \)
\( \LARGE g(x)=\frac{3x^2-4x+5}{x^2-4} \)
\( \LARGE h(x)=\frac{x-1}{x} \)
با توجه به تعریف چند جمله ایها تابع گویا نمی تواتد متغیرش زیر رادیکال یا داخل قدرمطلق باشد.
دامنه توابع گویا
در مورد دامنه توابع گویا باید گفت چون مخرج صفر بیمعنی است پس بزرگترین دامنه ممکن آنها برابر است با:
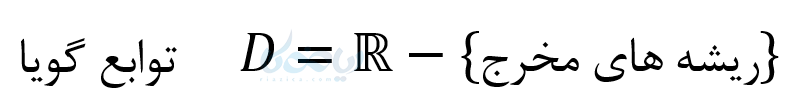
مثال: دامنه تابع زیر را پیدا کنید.
(1
\( \LARGE f(x)=\frac{1-3x}{x-2} \)
\( \LARGE D_f = \mathbb{R} – \{2\} \)
(2
\( \LARGE g(x)=\frac{x-1}{x^2-4} \)
\( \LARGE D_g = \mathbb{R} – \{-2,+2\} \)
(3
\( \LARGE h(x)=\frac{3x}{x^2-5x+6} \)
\( \LARGE D_h = \mathbb{R} – \{2,3\} \)
نکته :اگر تابع گویا ساده می شود ابتدا باید دامنه آن را بدست آوریم سپس آن را ساده کنیم .
آخر کلاس آموزش تابع گویا
تابع گویا با وجود سادگی، از توابعی است که بسیار با آن روبه رو خواهید شد. در این آموزش سعی کردیم این تابع را همراه با مثالهای متنوع و تشریح دامنه و برد آن برای شما بیان کنیم.
در صورتیکه هر سوالی در رابطه با این آموزش داشتید، میتوانید سوال خود را در بخش دیدگاههای این پست مطرح کنید. ما در ریاضیکا به سوالات شما پاسخ خواهیم داد.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!





سلام.اگر صورت یا مخرج کسر رادیکالی یا قدرمطلقی باشه گویا نیست.؟
سلام و عرض ادب
در مورد عبارت رادیکالی اگر رادیکال ساده نشود تابع گویا نیست.
در مورد قدرمطلق هم تابع اگر متغیر داخل قدر مطلق باشد گویا نیست
سلام استاد، درباره دیدگاه تون درباره قدر مطلق من پاسخنامه کتاب میکرو رو دیدم که میگفت قدر مطلق اگه تو تابع باشه گویا محسوب نمیشه، جسارتا در محدوده کنکوری نظر شما همون هست که فرمودید؟
با سلام دوست عزیز
بله درسته گویا نیست
سلام اگر در صورت کسر sin یا cos باشد گویا هست؟
با سلام دوست عزیز
در این صورت تابع گویا نیست بلکه تابع مثلثاتی میباشد
سلام استاد.اگر در نمودار تابع گویا حفره وجود داشته باشد چرا طول حفره(x) باید در صورت و مخرج صدق کند؟
با سلام اگر منظورتان از حفره مقادیری است که به ازای ریشه آنها کسربی معنی میشود برای همین آنها را حذف میکنیم