آموزش ریاضی پایه دهم
آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
در آموزش ترکیب در ریاضی پایه دهم یاد میگیریم چگونه چند شئ را از بین اشیا انتخاب کنبم. همچنین میتوانیم تعداد انتخابهایمان را از قبل محاسبه کنیم.
ترکیب یا انتخاب \( \Large k \) شی از \( \Large n \) شی متمایز
گاهی در مسائل ما میخواهیم از بین \( \Large n \) شئ فقط \( \Large k \) شئ را انتخاب کنیم و ترتیب قرارگرفتن اشیا برای ما مهم نیست. در واقع ترکیب انتخاب شده برای ما مهم است. مثلا فرض کنید یک مجموعهٔ 5 عضوی داریم و میخواهیم تعداد زیر مجموعههای 3 عضوی آن را بیابیم. میدانیم در مجموعه ترتیب قرارگرفتن اشیا مهم نیست. یعنی داریم:
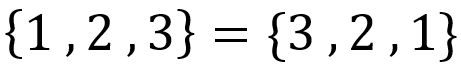
پس در این مثال از بین 5 عضو مجموعه، فقط میخواهیم ترکیبهای 3 تایی انتخاب کنیم. خب از طرفی میدانیم تعداد جایگشت های 3 عضو برابر است با \( \Large 3!=6 \). خوب اگر جایگشت های 3 عضو از 5 عضو را پیدا کنیم. داریم:
\( \LARGE P(5,3)=\frac{5!}{2!} \)
\( \LARGE =\frac{5 \times 4 \times 3 \times 2!}{2!} =60 \)
میدانیم این با در نظرگرفتن جایگشتهای 3 عضو انتخاب شده که مورد نظر ما نیست پس این تعداد را به !3 تقسیم میکنیم. داریم:
\( \LARGE \frac{60}{3!}=\frac{60}{6}=10 \)
یعنی از بین 5 عضو به 10 طریق میتوان 3 عضو را بدون در نظرگرفتن جایگشت های آن انتخاب کرد. پس فرمول بالا به صورت زیر استفاده میشود:
\( \LARGE C(5,3)=\frac{5!}{2!\times 3!}=10 \)
و به طور کلی داریم. ترکیب یا انتخاب \( \Large k \) شی از بین \( \Large n \) شی برابر است با:
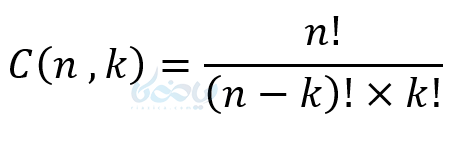
نکته آموزشی از ترکیب: این نماد را به صورت \( \Large nCk \) یا \( \Large \begin{pmatrix} n \\ k \end{pmatrix} \) هم نمایش میدهند.
نکته مهم: دانشآموزان عزیز برای یادگیری بیشتر میتوانید نوشتار آموزش جایگشت را از مجموعه آموزشهای ریاضی دهم ریاضیکا بخوانید.
مثال ۱: میخواهیم از بین 10 گل، دسته گلهای چهارتایی درست کنیم. این کار به چند طریق امکانپذیر است؟
حل ۱:
\( \LARGE C(10,4)=\begin{pmatrix} 10 \\ 4 \end{pmatrix} \)
\( \LARGE = \frac{10!}{4!\times 6!} = \frac{10 \times 9 \times 8 \times 7 \times 6!}{4!\times 6!} \)
\( \LARGE =210 \)
در این مسئله نیز فقط ترکیب گلها برای ما مهم است نه ترتیب قرارگرفتن آنها.
مثال ۲: یک مربی فوتبال از بین 20 نفر میخواهد یک تیم فوتبال تشکیل دهد، این کار به چند طریق امکانپذیر است؟
حل ۲:
\( \LARGE C(20,11)=\begin{pmatrix} 20 \\ 11 \end{pmatrix} \)
\( \LARGE = \frac{20!}{9!\times 11!} \)
مثال ۳: یک مربی فوتبال میخواهد از بین 11 نفر اعضای تیم یک نفر را برای دفاع راست یک نفر دفاع چپ و یک نفر را به عنوان دروازهبان انتخاب کند. این کار به چند طریق امکان پذیر است؟
حل ۳: در این مسئله نه تنها انتخاب 3 نفر مهم است، بلکه نحوه انتخاب آنها نیز مهم است که چه کسی از این سه نفر نیز دفاع راست چه کسی دفاع چپ و چه کسی دروازهبان باشد. پس تعداد جایگشتهای 3 نفر از 11 نفر را میخواهیم. یعنی داریم:
\( \LARGE P(11,3)=\frac{11!}{8!} \)
مثال 4: در کیسهای 4 مهره سفید و 5 مهره سیاه است. میخواهیم 3 مهره از این کیسه به تصادف انتخاب کنیم این کار به چند طریق امکان دارد. اگر:
الف) 2 مهره سفید و یک مهره سیاه باشند.
\( \LARGE \begin{pmatrix} 4 \\ 2 \end{pmatrix} \times \begin{pmatrix} 5 \\ 1 \end{pmatrix} \)
\( \LARGE = 6 \times 5 =30 \)
با توجه به اینکه 2 تا سفید و یکی سیاه پس طبق اصل ضرب به دست آوردیم.
ب) هر سه سیاه باشند.
\( \LARGE \begin{pmatrix} 5 \\ 3 \end{pmatrix} =10 \)
ج) هر سه همرنگ باشند.
\( \LARGE \begin{pmatrix} 5 \\ 3 \end{pmatrix} + \begin{pmatrix} 4 \\ 3 \end{pmatrix} \)
\( \LARGE =10+4=14 \)
یعنی یا هر سه سفید یا هر سه سیاه (اصل جمع)
د) حداقل یکی سیاه باشد.
\( \LARGE \begin{pmatrix} 5 \\ 1\end{pmatrix} \begin{pmatrix} 4 \\ 2 \end{pmatrix} \)
\( \LARGE + \begin{pmatrix} 5 \\ 2 \end{pmatrix} \begin{pmatrix} 4 \\ 1 \end{pmatrix} + \begin{pmatrix} 5 \\ 3 \end{pmatrix} \)
\( \LARGE =5 \times 6 + 10 \times 4 +10 \)
\( \LARGE =80 \)
حداقل یکی سیاه یعنی یا یکی سیاه و 2 تا سفید یا دو تا سیاه یکی سفید یا هر سه سیاه (اصل ضرب و جمع)
برای محاسبه سریعتر مسائل مربوط به آموزش ترکیب ، قوانین زیر را به خوبی فرا بگیرید.
قوانین ترکیب (\( \Large k \) شئ از \( \Large n \) شئ)
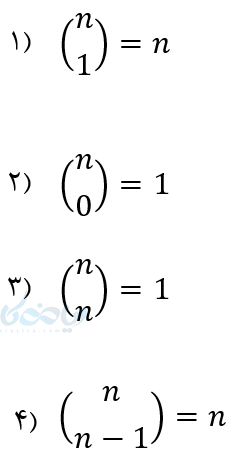
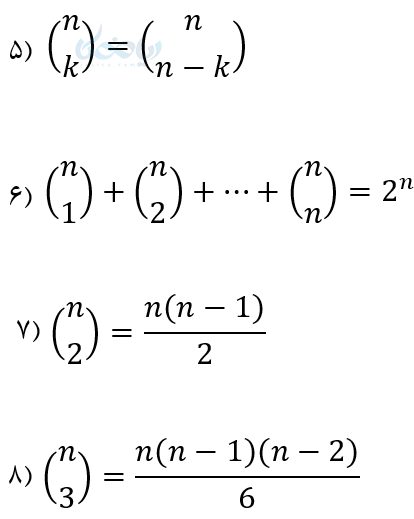
مثال برای قانون 4:
(1
\( \LARGE \begin{pmatrix} 4 \\ 3 \end{pmatrix} =4 \)
(2
\( \LARGE \begin{pmatrix} 7 \\ 6 \end{pmatrix} =7 \)
مثال برای قانون 5:
(1
\( \LARGE \begin{pmatrix} 7 \\ 3 \end{pmatrix} = \begin{pmatrix} 7 \\ 4 \end{pmatrix} \)
(2
\( \LARGE \begin{pmatrix} 12 \\ 5 \end{pmatrix} = \begin{pmatrix} 12 \\ 7 \end{pmatrix} \)
مثال برای قانون 6:
\( \LARGE \begin{pmatrix} 5 \\ 1 \end{pmatrix} + \begin{pmatrix} 5 \\ 2 \end{pmatrix} + .. + \begin{pmatrix} 5 \\ 5 \end{pmatrix} \)
\( \LARGE =2^5=32 \)
مثال برای قانون 7:
\( \LARGE \begin{pmatrix} 10 \\ 2 \end{pmatrix}=\frac{10 \times 9}{2} \)
\( \LARGE = 45 \)
مثال برای قانون 8:
\( \LARGE \begin{pmatrix} 10 \\ 3 \end{pmatrix}=\frac{10 \times 9 \times 8}{6} \)
\( \LARGE = 120 \)
ویدیو از آموزش ترکیب در ریاضی دهم
در این ویدیو ترکیب اشیا واعداد از بین چند شی و عدد با مثال توضیح داده شده و قوانین ترکیب نیز بیان شده است.
زنگ آخر کلاس آموزش ترکیب
بچهها در این نوشتار با آموزش ترکیب و یا انتخاب \( \Large k \) شئ از \( \Large n \) شئ متمایز و قوانین ترکیب (\( \Large k \) شی از \( \Large n \) شی) آشنا شدیم. همچنین این مبحث مهم را با مثالهای مهم و مفهومی باهم به خوبی بررسی کردیم.
مباحث مهم دیگری از آموزش ریاضی دهم را میتوانید در همین سایت بخوانید. هرسوالی که از این نوشتار آموزشی داشتید را میتوانید در پایین هم بخش در قسمت دیدگاهها برای ما بنویسید. بچههای ریاضیکا حتماً به سوالات شما پاسخ میدهند. شاد و پیروز باشید 🙂
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!





سلام ببخشید آیا این سوال رو میشه بدون استفاده از متمم حل کرد؟چگونه؟
سوال:(یک آشپز 10 نوع ادویه دارد از هر سه تا از این ادویه ها یک طعم مخصوص درست می کند،این آشپز چند طعم می تواند درست کند زمانی که دو نوع ادویه هستند که نمی توانند با هم استفاده شوند؟؟
با سلام وعرض ادب
بله میشه این سوال کتاب هست از دبیرتون بپرسید جواب میدهن
دستتون درد نکنه برای مرور درس عالی بود
با سلام وقت به خیر
ممنون از لطف شما
بسیار مطلب مفیدی بود
این مطلب رو برای ازمون ارشد مطالعه کردم ،تمام ریاضیات دبیرستانم که مربوط به این مبحث بود برام دوره شد.سپاس
با سلام ودرود
خدا رو شاکریم که برای همه سطوح مفید هست مطالب سایت ما
سلام میشه لطف کنید اثبات ترکیب n از n رو بزارید توی سایت؟
با سلام وادب
فرمولش رو بنویس با توجه به اینکه صفر فاکتوریل میشه یک حله واثبات میشه که میشه یک
سلام استاد
لطفا سمت چپ فرمول شماره 6 را اصلاح فرمایید .
ممنون از دقت نظر شما اصلاح میشه
سلام
ممنون و خدا قوت
خدا خیرتون بده برای امتحان آمار دانشگاهم که فرمولارو یادم رفته بود خیلی سریع تونستم با این مطالب مرورشون کنم🙏🏻🌷سپاس🌹
با سلام وادب
خدا رو شاکریم که مطالب سایت برای همه کاربردی ومفید هست
سلام وقت بخیر
ممنون از مطلب شما
با سلام ممنون از نگاه شما
اینقدری که دقیق و بی نقص بود تازه فهمیدم ریاضی یعنی چی… واقعا دستتون درد نکنه.. موفق باشید
سلام وقت بخیر ببخشید اثبات فرمول ترکیب به روش استقرای ریاضی چجوری میشه