آموزش ریاضی پایه یازدهم تجربی
آموزش معادله خط به زبان ساده 〽️📈 – قدم به قدم با مثال?
سلام به همه دانشآموزان و علاقهمندان ریاضی و ریاضیکا. در این آموزش میخواهیم در مورد آموزش معادله خط و طریقهٔ نوشتن معادله یک خط با استفاده از شیب صحبت کنیم .پس ابتدا شیب خط را تعریف کرده سپس نوشتن معادله خط را بیان می کنیم.
شیب خط
شیب یک خیابان یا یک جاده به دو کمیت ارتفاع و مسافت افقی طی شده بستگی دارد. یک نکته مهم که در آموزش معادله خط باید به آن توجه کنید این است که به طور کلی شیب یعنی نسبت ارتفاع به مسافت افقی طی شده. از رابطه شیب خط که در زیر آورده شده است، شیب خط را بدست میآوریم.

حال اگر دو نقطه زیر را در نظر بگیریم خواهیم داشت.
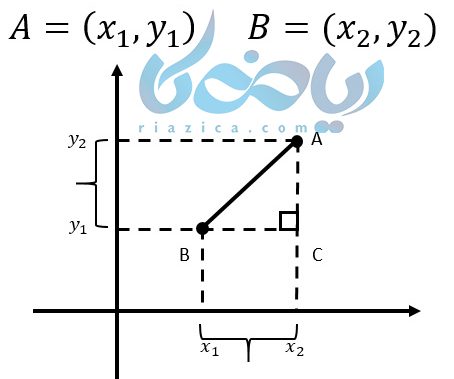
حال در مثلث ABC شیب خط AB به صورت زیر است :

نوشتن معادله یک خط
یک خط از بی نهایت نقطه تشکیل شده است که طول و عرض این نقاط باهم رابطه دارند. مثلاً خطی را در نظر بگیرید که از نقاط (1,2) و (2,4) میگذرد. این نشان میدهد که تمام نقاطی که روی این خط قرار دارند، عرضشان دو برابر طولشان است. این را به زبان ریاضی و آموزش معادله خط این گونه مینویسیم:
\( \Large y = 2x \)
در واقع معادله یک خط رابطهٔ بین طول و عرض نقاط واقع بر یک خط را نشان میدهد. اما تشخیص این رابطه و نوشتن معادله یک خط همیشه به این آسانی نیست. برای نوشتن معادله یک خط حداقل دو نقطه از آن را نیاز داریم. در نهایت با استفاده از رابطهٔ شیب خط که در زیر آورده شده است، شیب خط را بدست میآوریم:
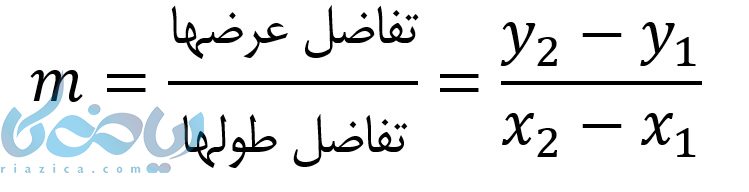
سپس شیب و مختصات یکی از نقاط را در معادله کلی خط یعنی \( \LARGE y = ax + b \) که در آن \( \LARGE a \) شیب خط و \( \LARGE b \) عرض از مبدا است، قرار میدهیم. در نهایت \( \LARGE b \) را پیدا میکنیم.
مثال ۱: معادله خطی که از دو نقطه (1,2) و (5,3) میگذرد را بنویسید.
حل ۱:
\( \LARGE m = \frac{3-2}{5-1} = \frac{1}{4} \)
\( \LARGE y = ax + b \)
\( \LARGE 2 = 1 \times \frac{1}{4} + b \)
\( \LARGE b = \frac{7}{4} \Rightarrow y = \frac{1}{4} x + \frac{7}{4}\)
پس به طور کلی برای نوشتن معادله یک خط به شیب و یک نقطه از خط نیاز داریم.
مثال ۲: \( \Large m=3 \) شیب خطی است و محور طولها را در نقطهای به طول 2 قطع میکند. معادله این خط را بنویسید.
حل ۲:
\( \LARGE m = 3 , (2,0) , y = ax + b \)
\( \LARGE 0 = 2 \times 3 + b \)
\( \LARGE b = -6 \)
\( \LARGE y = 3x – 6 \)
آموزش معادله خط : شیب خطوط موازی و عمود
برای خطها دو حالت خاص را میتوان در نظر گرفت که به راحتی با معادله خط آنها قابل تشخیص است:
- خطوط موازی
- خطوط عمود
۱- خطوط موازی
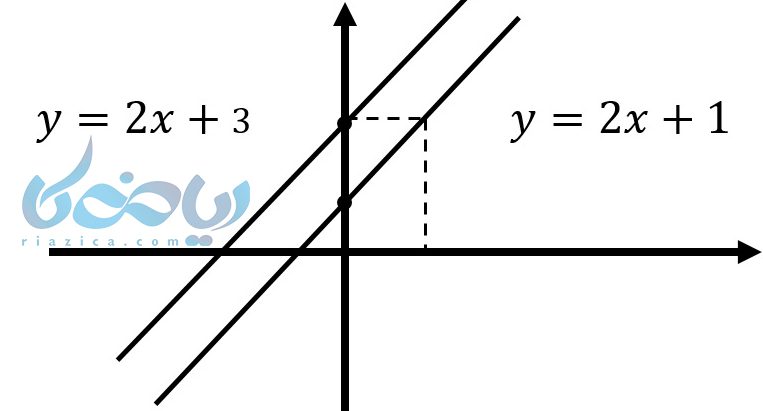
اگر دو خط با هم موازی باشند شیبهایشان برابر است. در اصل شیب یعنی مقدار کج و راستی یک خط. خط هایی با شیب برابر با هم موازیاند. بعنوان مثال دو خط زیر را در نظر بگیرید:
\( \Large y = 2x + 3 \) و \( \Large y = 2x + 1 \)
این دو خط با هم موازی هستند و فقط عرض از مبدا آنها با هم فرق میکند. درنتیجه مقدار \( \LARGE a \) (همان شیب) در خطوط موازی حتماً برابر است.
۲- خطوط عمود بر هم
دو خط عمود برهم شیبهایشان قرینه و معکوس یکدیگر است. طوریکه حاصلضرب شیبهای آنها منفی یک میشود.
\( \Large mm’ = -1 \)
\( \Large y = 2x+2 \)
\( \Large \Rightarrow y = -\frac{1}{2} x + 3 \)
فرم های کلی معادله خط ها وشیب آنها
در آموزش معادله خط می آموزیم معادله یک خط را می توان به دو فرم کلی زیر نوشت
\( \LARGE 1) y = ax + b \\ \LARGE 2) ax + by + c = 0 \)
در فرم اول \( \LARGE a \) شیب خط و \( \LARGE b \) عرض از مبدا است.
ولی در فرم دوم شیب خط و عرض از مبدا به صورت زیر میباشند:
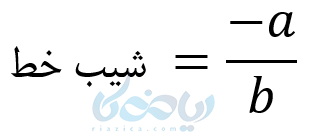
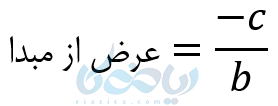
پس اگر مختصات دو نقطه را داشته باشیم و شیب را بخواهیم پیدا کنیم از رابطه ی زیر استفاده میکنیم:

ولی اگر معادله خط را داشته باشیم از روی معادله، شیب را پیدا میکنیم.
اگر خط صعودی باشد، یعنی با افزایش مقدار x مقدار y نیز افزایش پیدا کند شیب خط مثبت میشود.
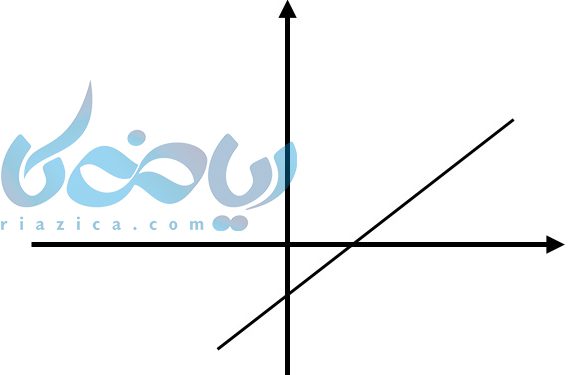
اگر خط نزولی باشد یعنی با افزایش مقدار \( \LARGE x \) مقدار \( \LARGE y \) نیز کاهش پیدا کند شیب خط منفی میشود.
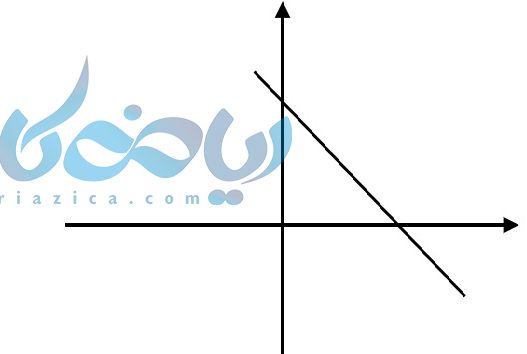
یک نکته مهم: به طور کلی نمودار از چپ به راست خوانده میشود. در نتیجه اگر خط به سمت بالا برود خط صعودی و اگر به سمت پایین برود خط نزولی میشود.
معادله خط های استثناء
دو حالت استثناء را میتوان برای شیب خط ها در نظر گرفت:
- خط موازی محور افق(طولها)
- خط موازی محور قائم(عرضها)
معادله خطوط موازی محور افق(طولها) وشیب آنها
اگر خطی مانند خطی که در شکل زیر قرار دارد موازی محور \( \Large x \)ها باشد، تمام نقاط واقع بر آن داری عرض یکسان هستند. در نهایت معادله این خط به \( \Large x \) بستگی ندارد. پس معادله آن به صورت \( \Large y = b \) است که \( \Large b \) همان عرض از مبدأ است. عرض از مبدأ جایی است که خط مورد نظر ما، محور عرضها را قطع میکند. شیب این خطها صفر است. زیرا:
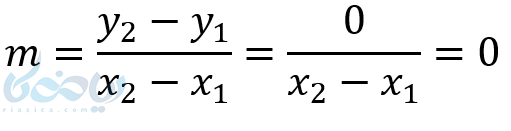
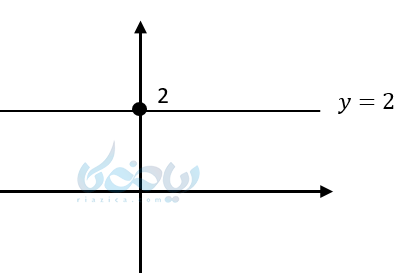
معادله خطوط موازی محور قائم(عرضها) وشیب آنها
اگر خطی موازی محور \( \Large y \)ها باشد، مانند خطی که در شکل زیر قرار دارد، تمام نقاط واقع بر آن دارای طول یکسان هستند. در نهایت معادله این خط ها به صورت \( \Large x = a \) است. \( \LARGE a \) جایی است که خط محور \( \Large x \) ها را قطع میکند. شیب این خط ها تعریف نشده است. زیرا:
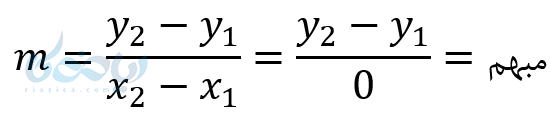
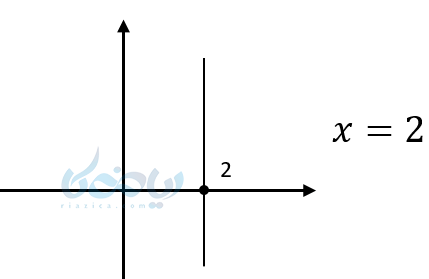
مثال۳: معادله خطی را بنویسید که از نقاط (5,2) و (3,2) بگذرد؟
حل۳: چون تمام نقاط عرضشان 2 است پس معادله خط برابر است با \( \Large y = 2 \)
چند مثال برای درک بهتر از آموزش معادله خط
مثال ۴: معادله خطی را بنویسید که از نقاط (2,3-),(1,2) بگذرد ؟
حل ۴:
\( \LARGE m = \frac{3-2}{-2-1} = \frac{1}{-3} \)
\( \LARGE y = ax + b \)
\( \LARGE 2 = 1 \times – \frac{1}{3} + b \)
\( \LARGE b = \frac{7}{3} \Rightarrow y = \frac{-1}{3} x + \frac{7}{3}\)
مثال ۵: معادله خطی را بنویسید که از نقاط (2,3) و (2,8) بگذرد ؟
حل ۵: چون نقاطی که روی این خط هستند طولشان 2 است پس معادله خط مورد نظر برابر است با \( \Large x = 2 \).
مثال ۶: معادله خطی را بنویسید که از نقطه (3,1) گذشته و برخط \( y = \frac{-1}{2}x + 2 \) عمود باشد؟
حل ۶:
\( \LARGE m = 2 \)
\( \LARGE 1 = 3 \times 2 + b \)
\( \LARGE b = -5 \)
\( \LARGE y = 2x – 5 \)
رابطه شیب با تانژانت در معادله خط
اگر خطی موازی محور \( \Large x \)ها نباشد، حتماً محور \( \Large x \)ها را در یک نقطه قطع میکند و با آن دو زاویه میسازد. جز خط هایی که موازی محور \( \Large x \) ها میباشند زاویه ای که سمت راست قرار دارد را در نظر بگیرید. شیب خط با \( \LARGE tan \) این زاویه برابر است.
زیرا:
\( \LARGE tan\theta = \frac{AB}{BC} \)
از طرفی طبق تعریف شیب:
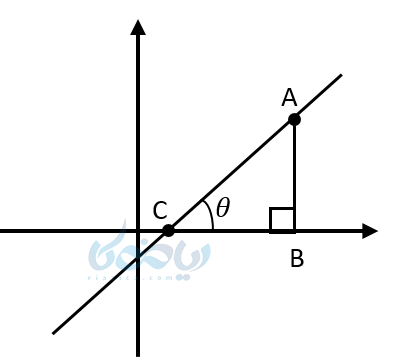

مثال ۷: معادله خطی را بنویسید که با جهت مثبت محور \( \Large x \)ها زاویه 45 بسازد و محور عرضها را در نقطه 2 قطع کند؟
حل ۷:
\( \LARGE m = tan45 = 1 \)
عرض از مبدا:
\( \LARGE b = 2 \)
پس
\( \LARGE y = x + 2 \)
مثال ۸: خطی از نقاط \( (-2 , 0 ) , (1 , \sqrt[2]{3} ) \) میگذرد. این خط با محور \( \Large x \)ها چه زاویهای میسازد؟
حل ۸:
\( \LARGE m = \frac{\sqrt{3} – 0}{1 – (-2) } = \frac{\sqrt{3}}{3} \)
\( \LARGE m = tan30 = \frac{\sqrt{3}}{3} \)
آموزش معادله خط و نقطه وسط یک پاره خط
اگر مختصات دو سر یک پاره خط را داشته باشیم و مختصات نقطه وسط یک پاره خط را بخواهیم، از رابطه زیر استفاده میکنیم:
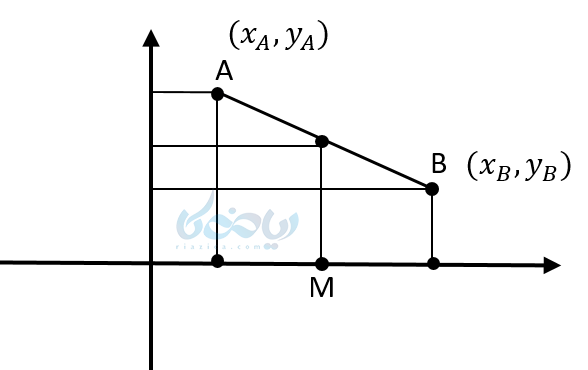
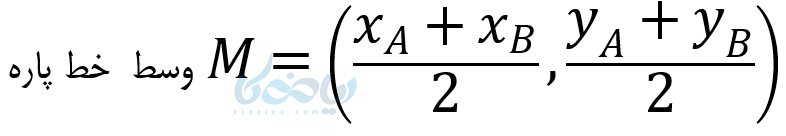
مثال ۹: اگر (4,3),(2,1) دو سر یک پاره خط باشند مختصات نقطه وسط این پاره خط را به دست آورید؟
حل ۹:
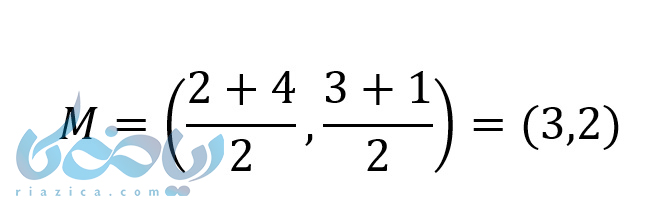
طول پاره خط AB
نقاط زیر را در نظر بگیرید. اگر بخواهیم با کمک آموزش معادله خط طول پاره خط \( \Large AB \) را بیابیم، طبق شکل و رابطه فیثاغورس خواهیم داشت:
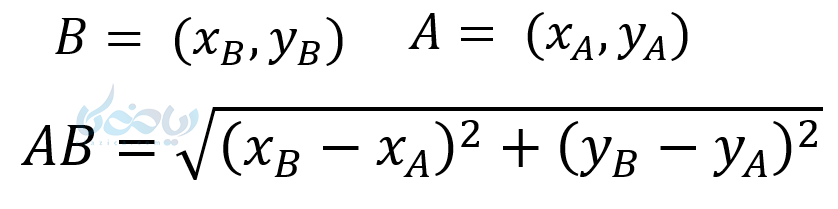
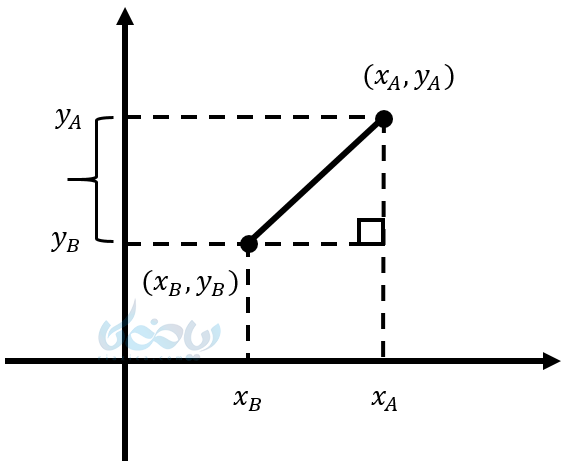
مثال ۱۰: طول پاره خط \( \Large AB \) را بدست می آورید اگر داشته باشیم : \( A = (2,1) \) و \( B = (3,5) \)
حل ۱۰:
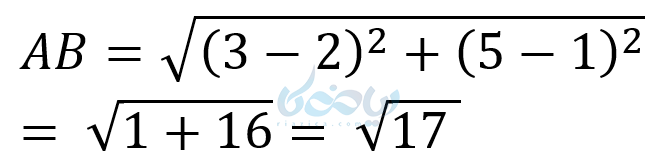
فاصله نقطه از خط در آموزش معادله خط
به شکل زیر دقت کنید. نقطه \( \Large A \) خارج از خط \( \Large d \) قرار دارد. میخواهیم فاصله این نقطه تا خط \( \Large d \) را پیدا کنیم. میدانیم کوتاهترین فاصله بین نقطه \( \Large A \) و خط \( \Large d \)، خط عمود گذرنده از \( \Large A \) میباشد. برای پیدا کردن این فاصله به مختصات نقطه \( \Large A \) و معادله خط \( \Large d \) به فرم گسترده نیاز داریم.

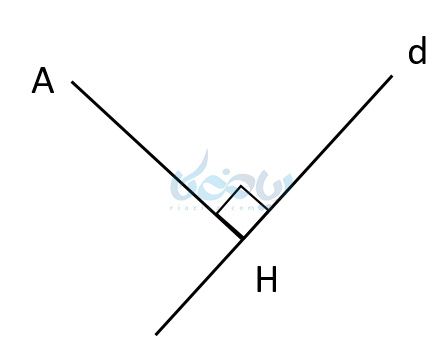
مثال ۱۱: فاصله نقطه (A=(1,2 از خط روبرو را بدست آورید؟ (\( \Large 3x-4y=5 \))
حل ۱۱:
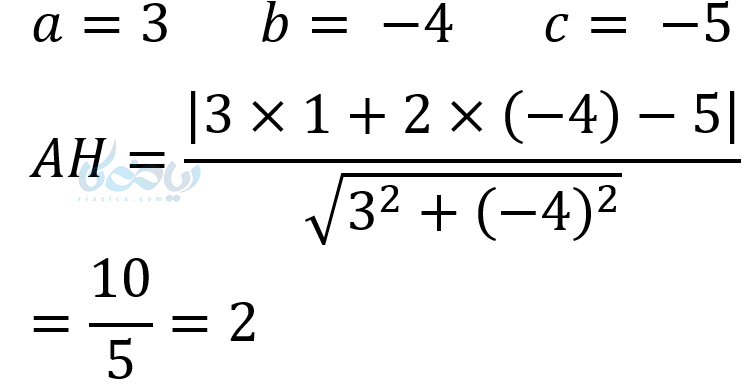
سوال های شما در نورد معادله خط
مثال ۱۲: معادله خطی بنویسید که محور طولها را در نقطهای به طول 2 قطع کند و موازی خط به معادله \( \Large \frac{x}{2} + \frac{y}{3}=1 \) باشد.
حل ۱۲:
چون بیان کرده که موازی باشد پس شیب خط درخواستی با شیب \( \Large \frac{x}{2} + \frac{y}{3}=1 \) برابر است.
\( \LARGE \frac{x}{2} + \frac{y}{3}=1 \)
\( \LARGE \frac{y}{3}=1-\frac{x}{2} \)
\( \LARGE y=3-\frac{3x}{2} \)
\( \LARGE a=-\frac{3}{2} \)
سوال به ما نقطه \( \Large (2,0) \) را نیز داده است چون خط درخواستی محور طولها را در نقطه ۲ قطع کرده است.
\( \LARGE y=ax+b \)
\( \LARGE a=-\frac{3}{2} , (2,0) \)
\( \LARGE 0=-\frac{3}{2} \times 2 + b \)
\( \LARGE b=3 \)
\( \LARGE y=-\frac{3}{2} x + 3 \)
توصیه میشه قبل از خوندن این پست ،پست معادله خط نهم را هم مطالعه کنید.
آخر زنگ آموزش معادله خط
در این نوشتار سعی کردیم آموزش معادله خط را همراه با مثالهای متنوع برای شما دانشآموزان و علاقمندان به ریاضیات بیان کنیم. تمام تلاش ما در ریاضیکا آموزش ریاضی به بیانی ساده و شیوا است.
در صورتیکه که هرگونه سوالی از این مبحث داشتید، میتوانید آن را در قسمت دیدگاهها در پایین همین نوشتار بنویسید. کارشناسان ما در ریاضیکا به سوالات شما پاسخ خواهند داد.




سلام با عرض خسته نباشید از آموزش کاملتون.
فاصله دو خط موازی چه جوری پیدا کنیم.
مرسی.
سلام بر شما دوست عزیز.
به وسیله فرمول، فاصله نقطه از خط.
عالی بود دمتون گرم ??
خواهش میکنم
موفق باشید ??
ممنون از توضیحاتتون. واقعا بهم کمک کرد.
سپاسگزارم
ضمن عرض سلام
خیلی خوشحالیم که تونستیم کمکی به شما کرده باشیم
سپاسگزار خواهیم بود اگر ما رو به دوستانتون معرفی کنید
موفق و پیروز باشید.
معادله خطو هرچی کلیپ نگاه میکنم یاد نمیگیرم میشه کامل توضیح بدین
با سلام دوست عزیز
در این پست به ساده ترین زبان گفتیم خواستید به صورت خصوصی در خدمت شما هستیم
سلام من یه معادله خط دارم و سوال داده که مختصاتی پیدا کنید ازش که طول و عرض ان مساوی باشد اینو چطوری حل کنم
سلام و وقت به خیر
کافی است به جای x، y را قرار دهید.
یعنی به جای عرض، طول را میگذاریم.
یک معادله یک مجهولی بدست میآید که درنهایت طول و عرض محاسبه میشود.
باسلام عالی بود فقط یک سوال داشتم خط موازی با y=3x+2چیست؟؟؟؟
سلام و وقت بخیر
شیب این خط ضریب x یعنی ۳ است. پس هر خطی که شیب آن ۳ باشد، با این خط موازی است. یعنی بی نهایت خط وجود دارد که با عرض از مبداهای مختلف که با این خط موازی هستند.
سلام جواب سوال معادله خطی را بنویسید که محور طول ها را در نقطه ای به طول 2 قطع کند و موازی به خط معادله x\2 +y\3 =1 باشد چیست
سلام دوست عزیز.
جواب می شود :
y=-3/2x+3
در آپدیت این نوشتار می توانید جواب کامل راببینید.
سلام جواب سوال معادله خطی بنویسید که محور طول ها را در نقطه ای به طول 2 قطع کند و موازی خط به معادله x\2 +y\3 =1 باشد چیست
سلام دوست عزیز.
جواب می شود :
y=-3/2x+3
در آپدیت این نوشتار می توانید جواب کامل راببینید.
خطی با شیب m از نقطه (2,1) گذشته و محور های مختصات را در A و B قطع می کند m را به گونه ای بیابید که مساحت مثلث OAB برابر چهار شود
سلام ببخشید میشه به این سوال جواب بدین
ضابطه ی تابع خطی را بیابید که از دو نقطه ی (۲,۴) A و(۴,۶) B می گذرد
با عرض سلام واحترام
دقیقا مانند مثال سه عمل کنید
سلام وخسته نباشید معادله خطی بتویسید که از سه نقطه a, b ,c بگذرد مختصات نقاط داده شده است
با سلام
با استفاده از دو تا نقطه ها شیب رو پیدا کنید ومانند مثالهای حل شده رد پست معادله رو بنویسید
معادله خطی که از نقطه A با مختصات (۳-،۲)میگذرد تا زاویه ۵x /۶ بسازد
با سلام وعرض ادب
صورت سوال درست نیست
سلام ببخشید میشه لطفا این سوال رو حل کنید ممنون میشم
معادله تمام خطوطی که از نقطه(۰و۱) میگذرند بنویسید
با سلام وعرض ادب
از یک نقطه بی نهایت خط میگذرد پس نمی توان معادله همه رو نوشت
بله خیلی ممنون?
با سلام وعرض ادب
خواهش میکنم
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
با سلام و احترام
آیا میشود بدون داشتن مختصات دو نقطه محور x و فقط با دو نقطه محور y شیب خط را حساب کرد؟
با سلام
اگر هر دو نقطه روی خوذ محورعرضها باشنذ طولشان صفر است و شیب تعریف نشده است
محور x تاریخ هست و محور y قیمت و به نظرم برای محور x نمیشه عدد در نظر گرفت
آیا میشه یک عدد دستی وارد کرد مثلاً 1 برای نقطه اول و 2 برای نقطه دوم
با سلام
بله، می شود برای هر تاریخی یک عددی را مشخص کرد یا خود تاریخ را زیر محور بنویسید.
رای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
بسیار مفید
با سلام وعرض ادب
خوشحالیم که مفید واقع شده
سلام
خیلی خوب بود.
ممنون از سایتتون
با سلام واحترام
ممنون از توجه شما
ببخشید میشه جواب این سوال رو بدین
معادله ی خطی را بنویسید که از دو نقطه ی طول ۲ عرض ۶ و طول منفی ۴ و عرض ۳ بگذرد
با سلام واحترام
دوست عزیز اگه پست رو خوب بخونید به جواب میرسید
سلام
وقتی به ما یک معادله خط میدن چجوری میتونیم به طور دقیق نقطه رو پیدا کنیم
با سلام وعرض ادب
کافیه هر چند تا نقطه میخواهی به ایکس مقدار بدی وو وای رو بدست بیاری
سلام من یک سوال داشتم من همیشه در پیدا کردن نقاط برای یک معادله خط مشکل دارم چجوری میتونم با یک فرمول مشخص به جواب درست برسم ؟
با سلام وعرض ادب
خیلی راحت به ایکس مقدار بده تو معادله ووای رو بدست بیار
سلام ممنون از توضیحات خوبتون ببخشید به سوال داشتم :
اگر سوال ضابطه دو تابع رو بده و از ما نقطه ای که این دو تا تابع هم دیگه رو قطع میکنن رو بخواد
چه طور باید عمل کنیم ؟؟
با سلام وعرض ادب
بهترین روش رسم نمودار دو تابع وپیدا کردن محل برخورد آنها
سلام خسته نباشید واقعا توضیحات کامل بود حتی از کتاب خودمون.من در یک سوال گیر کردم اگه میشه کمکم کنید.
سوال=از نقطه A به طول 2 که روی خط 2x+y=3 است، خطی عمود بر 4x_3y=7 رسم کرده ایم. معادله این خط چیست؟
با سلام وروز به خیر
کافیه این نفطه رو بگذارید داخل معادله خط اولی تا عرض نقطه بدست بیادوشیب خط دومی رو پیدا کنید وقرینه ومعکوسش کنید وبا اون نقطه معادله خط رو بنویسید
معادله خطی بنویسید که از نقطه (2 , 3 _)A گذشته و زاویه آن با محور x ها ۳۰ باشد
اینو چطور میشه حل کرد؟
با سلام وعرض ادب
شیب خط با تانژانت زاویه ای که خط یا جهت مثبت محور ایکسها میسازه برابر هست پس شیب این خط رو بهتون داده بذارید تا نقطه داده شده در معادله خط وبدستش بیارید
سلام
جواب این سوال : «معادله خطی که از نقطه ای به طول ۵ و عرض ۱_ گذشته و بر خط x=۳ عمود باشد چیست » چی میشه ؟
با سلام وعرض ادب
خطی که براین خط عمود است شیبش صفر ایت و فقط عرض از مبدا دارد پس معادله اش میشود y=-1
ببخشید ، دو خطی که با هم زاویه 60 میسازن شیبشون چه ارتباطی با هم دارند ؟
با سلام وعرض ادب
شیب خط برابر با تانژانت زاویه ای که دو خط با هم میسازند
چقدرررررررر سایت عالی دارین واقعااا عالیه مرسی
با سلام و عرض ادب
خوشحالیم که برای شما مفید واقع شده
ba salam va tashakkor.
javabe test 1 eshtebah mibashad. lotfan tashih namaied.
با سلام وعرض ادب
ممنون از دقت نظر شما تصحیح شد
سلام
ممنون از توضیحاتتون
جواب این سوال بی زحمت:معادله خطی را بنویسید که از نقطه (2-و6):A بگذرد و مجموع طول از مبدا و عرض از مبدا ان 5 باشد.
سلا م ممنونم از توضیح عالی تون ، فقط یه سوال داشتم ، معادله خطی که از دونقطه [۳,۸_] و[۲_,۱_] عبور می کند چیست؟؟
با سلام
اگه پست رو خوب بخونید خودتون میتونید بنویسید
سلام بخشید این سوال با کدوم راه حل،حل میشه؟؟
معادله نیمساز دو خط 3x+4y=3 و ۴x+3y=3 کدام میتواند باشد؟
سلام وقتی معادله خط رو داریم چطور مثلثی که این خط میسازه رو مساحتش رو بدست بیاریم؟
با سلام وادب
باید مختصات نقاطی که خط محورها رو قطع میکنه پیا کنید مساحت مثلث قائم الزاویه ای که خط با محورها میسازه رو بدست میاریم
سلام و عرض ادب
چطور میشه قرینه یک خط رو نسبت به یک خط دیگه پیدا کرد؟
با سلام
بله میشه همون قرینه محوری روی خطی که میخواهید قرینه اش رو بدست بیارییم دوتا نقط پیدا میکنیم وقرینه اش رو نسبت به خط مورد نظر پیدا کرده وبه هم وصل میکمیم
سلام چطوری b را در معادله ها بدست می اورید
با سلام ادب
وقتی شیب رو بدست آوردیم میذاریم در معادله خط تا بی بدست بیاد
سلام میشه جواب این سوال رو بهم بگید
معادله خطی بنویسید ک از نقطه(3,1)بگذرد و باخط گذرنده از نقاط(_۲ ،۳) و (۵، _۶) موازی باشد
سلام…. ضمن تشکر از جنابعالی به خاطر مطالب مفید و بسیار عالیتون…. خدا به شما خیر بده
با سلام وادب
ممنون از نگاه زیبابین شما دوست عزیز
عالی
عالی