آموزش ریاضی پایه دهم
تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
در این نوشتار میخواهیم باهم در رابطه با تجزیه عبارت های جبری صحبت کنیم. این مبحث از سری آموزش ریاضی دهم است که در عین سادگی از اهمیت بالایی برخوردار است وکاربرد زیادی در ریاضیات دارد.
مفهوم تجزیه عبارت های جبری
تجزیه عبارت های جبری بدان معناست که:
یک عبارت جبری که به صورت مجموع یا تفاضل چند جمله است و یا به عبارت بهتر یک چند جملهای را به صورت حاصلضرب دو یا چند چند جملهای درآوریم.
مثلاً:
\( \LARGE a^2 + 3a + 4ab \)
\( \LARGE = a (a + 3 + 4b) \)
در اینصورت به هر یک از چند جملهایها شمارنده چند جملهای اولیه میگویند و چند جملهای اولیه مضرب این چند جملهایهای جدید است.
در مثال بالا \( \Large a , a+3+4b \) شمارندههای \( \Large a^2 + 3a + 4ab \) هستند. \( \Large a^2 + 3a + 4ab \) هم مضرب \( \Large a \) و هم مضرب \( \Large a + 3 + 4b \) است.
نکته ۱: وقتی صحبت از تجزیه میشود باید تجزیه با ضرایب صحیح و غیررادیکالی انجام گیرد. چون جملات با ضرایب غیرصحیح طبق قرارداد مضرب چندجملهایها محسوب نمیشوند.
روشهای تجزیه عبارت های جبری
- فاکتورگیری (عامل مشترکگیری)
- استفاده از اتحادها
- دستهبندی و فاکتورگیری
- شکستن و دستهبندی
1- فاکتورگیری یا عامل مشترکگیری
یکی از مهمترین روشهای تتجزیه عبارت های جبری روش فاکتورگیری یا همان عامل مشترکگیری است. در این روش:
- ابتدا ب.م.م (بزرگترین مقسوم علیه مشترک) جملات را پیدا میکنیم که در واقع تمام جملات به آن بخش پدیر هستن.ب.م.م عبارت های جبری برابر راست با حاصلضرب عاملهای مشترک با توان کمتر. یا به زبان سادهتر در مورد ضرایب عددی ب.م.م آنها را پیدا میکنیم. در مورد متغیرها نیز ، متغیرهای مشترک با توان کمتر را انتخاب میکنیم
- سپس تمام جملات را به ب.م.م تقسیم میکنیم. به مثال زیر دقت کنید:
\( \LARGE 4a^{2}b + 8a^{4}b^{3}c \)
\( \LARGE + 24a^{2}b^{2}c^{2} \)
در این مثال ب.م.م ضرایب 4 است. به عبارتی تمام ضرایب عددی به ۴ بخشپذیر هستند. عامل مشترک تمام جملات \( \Large a^2 , b \) است. همانطور که دقت میکنیم در مورد متغیرهای مشترک توان کمتر انتخاب میشود. پس از ب.م.م یا همان عامل مشترک \( \Large 4a^{2}b \) فاکتور میگیریم. یعنی تمام جملات را به این جمله تقسیم کرده و بعد از ساده کردن جواب نهایی را مینویسیم.
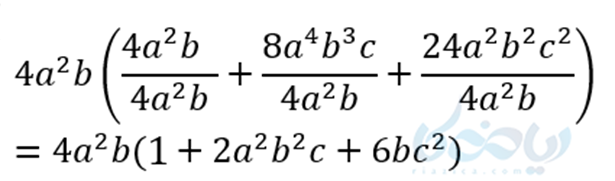
همانطور که مشاهده کردید این سه جملهای به صورت حاصلضرب یک «یکجملهای» و یک «سهجملهای» درآمد، این یعنی تجزیه.
نکته ۲: کار تقسیم را ذهنی انجام میدهیم و فقط جواب آخر را می نویسیم. به مثال دیگری در زیر دقت کنید:
(1
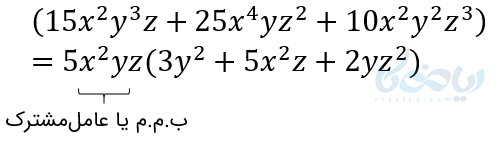
(2
\( \LARGE 17a^4 – 5a^2 \)
\( \LARGE = a^2(17a^2 – 5) \)
(3
\( \LARGE 3abc+9a^{2}b^{2}c\)
\( \LARGE +18a^{3}bc^{2} \)
\( \LARGE = 3abc(1 + 3ab+ 6a^{2}c) \)
2- استفاده از اتحادها
در تجزیه عبارت های جبری ، گاهی چند جملهای داده شده را میتوان با استفاده از اتحادها تجزیه کرد. برای استفاده از این روش باید به اتحادهای جبری تسلط کامل داشته باشیم تا بتوانیم اتحاد مورد نظر را به راحتی شناسایی و عبارت را تجزیه کنیم.پس بهتر است ابتدا اتحادها را خوب فرا بگیرید.
الف) اتحاد مربع دوجملهای
اگر یک سهجملهای داشته باشیم که دو تا از جملات آن مربع کامل باشند، باید حدس بزنیم اتحاد مربع دوجملهای است. سپس حدس خود را امتحان کنیم. به مثال زیر دقت کنید:
\( \LARGE a^2 + 6a + 9 \)
در این سهجملهای دو جمله مجذور کامل یا همان مربع کامل داریم. حال از کجا مطمئن شویم که این جواب یک اتحاد مربع دوجملهای است:
- ابتدا جذر دوجملهای را مینویسیم. یعنی \( \Large a , 3 \).
- حال دقت میکنیم آیا دو برابر یکی در دیگری جمله وسط میشود.
- اگر این طور بود پس حدس ما درست است و تجزیه عبارت را مینویسیم.
\( \LARGE (a^2 + 6a +9 ) = (a+3)^2 \)
نکته ۳: علامت بین آنها را از جملهای که مجذور کامل نیست متوجه میشویم. به مثال دیگر در زیر دقت کنید:
\( \LARGE (4a^4 – 20a^{2}b + 25b^2) \)
\( \LARGE = (2a^2 – 5b)^2 \)
در این مثال هم ملاحظه میکنید دو برابر اولی در دومی جمله وسطی میشود. البته همیشه ترتیب جملات به همین شکل نیست. مثلاً:
\( \LARGE (16x^2 + y^2 -8xy) \)
\( \LARGE = (4x-y)^2 \)
اما اگر جملهای که مجذور کامل نیست دو برابر جذر دو جمله دیگر نباشد، میگوییم این عبارت به این روش تجزیه نمیشود. مثلاً:
\( \LARGE a^2 – 10a + 49 \)
در این عبارت با اینکه دو جمله مجذور کامل داریم. اما به روش اتحاد مربع دوجملهای تجزیه پذیر نیست.
نکته ۴: تمام عبارتهای جبری با ضرایب صحیح قابل تجزیه نیستند.
ب) تجزیه عبارت های جبری به روش اتحاد مزدوج
برای اینکه بتوانیم عبارتی را از این روش تجزیه کنیم باید دو جمله مجذور کامل باشند، اما یکی منفی باشد. به مثال زیر دقت کنید:
\( \LARGE a^2 – 4 \)
این عبارت هر دو مجذور کامل و یکی منفی است. پس میتوان از روش اتحاد مزدوج آن را تجزیه کرد. برای این کار جذر این دو جمله را به صورت دو دوجملهای مزدوج مینویسیم.
یعنی:
\( \LARGE a^2 – 4 = (a-2)(a+2) \)
مثال:
(1
\( \LARGE 25a^{4}b^{2} – 1 \)
\( \LARGE = (5a^{2}b-1)(5a^{2}b+1) \)
(2
\( \LARGE -9 + x^4 \)
\( \LARGE = x^4 – 9 \)
\( \LARGE = (x^2 – 3)(x^2 + 3) \)
به مثال زیر دقت کنید:
\( \LARGE a^5 – a \)
در این مثال به نظر نمیرسد اتحاد مزدوج باشد. ولی هر دو فاکتور \( \Large a \) را دارند. پس ابتدا فاکتورگیری میکنیم:
\( \LARGE a^5 – a = a(a^4 – 1) \)
بعد از فاکتورگیری ملاحظه میکنید عبارت داخل پرانتز اتحاد مزدوج است. پس دوباره قابل تجزیه است پس داریم:
\( \LARGE a^5 – a \)
\( \LARGE = a(a^4 – 1) \)
\( \LARGE = a(a^2 – 1)(a^2 + 1) \)
\( \LARGE = a(a – 1)(a + 1) \)
\( \LARGE \times (a^2 + 1) \)
نکته ۵: گاهی هم روش فاکتورگیری هم روش اتحاد برای تجزیه به کار گرفته میشود.
نکته ۶: در تجزیه عبارت های جبری بایدتا جایی که امکان دارد عبارت جبری تجزیه شود.
ج) تجزیه به روش اتحاد جمله مشترک
اگر یک سهجملهای داشته باشیم که یک جمله آن مربع کامل باشد، حدس میزنیم که این عبارت به روش اتحاد جمله مشترک تجزیه میشود. مانند:
\( \LARGE x^2 + 5x +6 \)
میدانیم در اتحاد جمله مشترک، یک جمله مشترک و دو جمله غیرمشترک داریم که درجواب این اتحاد یک جمله مجذور جمله مشترک است. پس ابتدا جذر جمله مربع کامل را میگیریم. در دو پرانتز مینویسیم:
\( \LARGE x^2 + 5x +6 \)
\( \LARGE = (x….)(x….) \)
جملات غیرمشترک یکبار جمع شده و در جمله مشترک ضرب میشوند و یکبار در هم ضرب میشوند. پس ما در این جا به دنبال دو عدد میگردیم که حاصلضرب آنها 6 و مجموعشان 5+ باشد که آن دو عدد 2+ و 3+ هستند. پس داریم:
\( \LARGE x^2 + 5x +6 \)
\( \LARGE = (x+3)(x+2) \)
گاهی به این راحتی دو عدد را نمیتوان پیدا کرد. به مثال زیر دقت کنید:
\( \LARGE x^4 – x^2 – 12 \)
\( \LARGE = (x^{2}….)(x^{2}….) \)
در این مثال به دنبال دو عدد میگردیم که حاصلضربشان 12 و مجموعشان 1- شود. اگر نتوانستید ذهنی این کار را انجام دهید ابتدا اعدادی که حاصلضربشان 12 میشود را پیدا کنید، یعنی:
\( \LARGE ,3 \times 4 \) \( \LARGE ,2 \times 6 \) \( \LARGE 1 \times 12 \)
حال میدانیم در جمع همیشه جواب ،علامت عدد بزرگتر را میگیرد پس به عددهای بزرگتر علامت حاصل جمع یعنی علامت 1- را میدهیم. یعنی:
\( \LARGE ,3 \times (-4) \) \( \LARGE ,2 \times (-6) \) \( \LARGE 1 \times (-12) \)
چون علامت 12 یعنی حاصلضرب منفی است پس باید عدد دیگر مثبت باشد. خوب حال دقت کنید مجموع کدام دسته منفی یک میشود؟
درست است 4- و 3 پس داریم:
\( \LARGE x^4 – x^2 – 12 \)
\( \LARGE = (x^2 + 3)(x^2 -4) \)
باز در اینجا پرانتز دوم از روش مزدوج باز هم تجزیه میشود. پس داریم:
\( \LARGE x^4 – x^2 – 12 \)
\( \LARGE = (x^2 + 3) \)
\( \LARGE \times (x-2)(x+2) \)
نکته ۷: پس گاهی از چند اتحاد همزمان برای تجزیه استفاده میشود.
حال به مثال دیگری دقت کنید:
\( \LARGE x^2 – 5xy -24y^2 \)
\( \LARGE = (x…y)(x…y) \)
پس دو جمله غیرمشترک باید شامل \( \Large y \) باشند. حال دنبال دو عدد میگردیم که ضربشان 24- و جمعشان 5- باشد. پس داریم:
\( \LARGE ,3 \times (-8) \) \( \LARGE ,4 \times (-6) \) \( \LARGE ,2 \times (-12) \) \( \LARGE 1 \times (-24) \)
\( \LARGE x^2 – 5xy – 24y^2 \)
\( \LARGE = (x + 3y)(x – 8y) \)
البته وقتی شما در اینکار مهارت پیدا کردید این مراحل را میتوانید ذهنی انجام دهید.
چند مثال دیگر در زیر برای شما آوردیم:
(1
\( \LARGE a^{2}x^2 – 7ax + 10 \)
\( \LARGE =(ax-2)(ax-5) \)
(2
\( \LARGE x^3 +3x^2 – 28x \)
\( \LARGE = x(x^2 + 3x-28) \)
\( \LARGE = x(x-4)(x+7) \)
(3
\( \LARGE x^4 -13x^2 +36 \)
\( \LARGE = (x^2 – 9)(x^2 – 4) \)
\( \LARGE = (x-3)(x+3)\)
\( \LARGE \times (x-2)(x+2) \)
(4
\( \LARGE 9x^2 -6x -8 \)
\( \LARGE = (3x+2)(3x-4) \)
در این مثال چون جمله مشترک ضریب دارد، ابتدا جمله \( \Large 6x \) را به جمله مشترک تقسیم میکنیم، یعنی:
\( \LARGE -\frac{6x}{3x} = -2 \)
پس دنبال دو عدد میگیریم که حاصلضرب آنها 8- و جمع آنها 2- باشد. که بعد از ضرب در جمله مشترک \( \Large -6x \) شده.
حال به نمونه دیگری که به کمک اتحاد جمله مشترک میتوان آن را تجزیه کرد، دقت کنید:
\( \LARGE 3x^2 -4x – 15 \)
در این سه جمله ای اصلاً جمله مجذور کامل نداریم. پس به نظر میرسد نمیتوان آن را از روش جمله مشترک تجزیه کرد. اما به کمک روشی که به روش \( \Large A \) معروف است میتوان آن را تجزیه کرد. به این صورت که ابتدا اسم این عبارت را \( \Large A \) میگذاریم تا یک تساوی داشته باشیم:
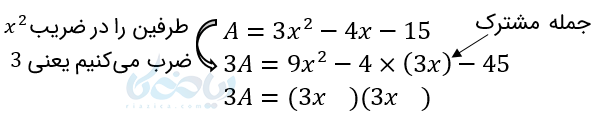
دنبال دو عدد میگیریم که حاصلضرب آنها 45- و مجموع آنها 4- باشد چون \( \Large 3x \) جمله مشترک است و برای همین \( \Large -4 \times 3x \) را یه این صورت نوشتیم داریم:
\( \LARGE 3A = (3x-9)(3x+5) \)
اما ما به جای عبارت داده شده سه برابر آن را تجزیه کردیم. پس از پرانتز اول به اندازه عدد 3 فاکتور میگیریم و با ضریب \( \Large A \) ساده میکنیم:
\( \LARGE 3A = 3(x-3)(3x+5) \)
\( \LARGE A = (x-3)(3x+5) \)
نکته ۸: برای تجزیه این عبارت از روش شکستن و دستهبندی که در ادامه آموزش میدهیم نیز میتوانید استفاده کنید.
مثالی دیگر برای شما میآوریم:
(\( \LARGE 6x^2 + 25x + 14 \))
\( \LARGE A = 6x^2 + 25x + 14 \)
\( \LARGE 6A = 36x^2 \)
\( \LARGE + 25 \times (6x) + 84 \)
\( \LARGE 6A = (6x+21)(6x+4) \)
\( \LARGE 6A = 2\times 3(3x+7) \)
\( \LARGE \times (3x+2) \)
در این مثال باید به اندازه ۶ واحد فاکتور بگیریم. اما چون هیچ کدام از پرانتزها به عدد 6 بخشپذیر نبودند از پرانتز اول 3 واحد و از پرانتز دوم 2 واحد فاکتور میگیریم.
نکته ۹: هر سه جملهای لزوما تجزیه پذیر نیست. مانند:
\( \LARGE x^2 – x +12 \)
د) تجزیه عبارت های جبری به روش اتحاد چاق و لاغر
از این روش وقتی میتوان استفاده کرد که دو جمله داشته باشیم که هر دو مکعب کامل باشند. مانند:
\( \LARGE a^3 – 8 \)
یا
\( \LARGE a^3 + 8 \)
حال برای تجزیه ابتدا کعب یا همان ریشه سوم دو جمله را پیدا میکنیم و علامت بین آنها همان علامت بین مکعبها است.
\( \LARGE a^3 – 8 = (a-2)( …..) \)
برای نوشتن سه جملهای این اتحاد از دو جمله ای کمک میگیریم، به این صورت که:

\( \LARGE a^3 – 8 \)
\( \LARGE = (a-2)(a^2 + 2a +4 ) \)
مثال:
(1
\( \LARGE a^3 +27 \)
\( \LARGE = (a+3)(a^2 -3a + 9 ) \)
(2
\( \LARGE a^{3}b^{6} – 1 \)
\( \LARGE = (ab^2 – 1) \)
\( \LARGE \times (a^{2}b^4 + ab^{2} + 1) \)
نکته ۱۰: در مورد اعداد، عددهای مکعب کامل را میشناسید. مانند:
\( \LARGE 1 , 8 , 27 , 64 , 125 , ….. \)
در مورد متغیرها اگر توان متغیر مضرب 3 باشد یعنی مکعب کامل است و وقتی کعب یا همان ریشه سوم میگیریم توان به 3 تقسیم میشود.
نکته ۱۱: در این روش هم گاهی از فاکتورگیری همراه این اتحاد استفاده میکنیم و تا حد امکان عبارت را تجزیه مینماییم.
(1
\( \LARGE a^4 – 125a \)
\( \LARGE = a(a^3 – 125) \)
\( \LARGE = a(a-5) \)
\( \LARGE \times (a^2 +5a + 25) \)
(2
\( \LARGE a^6 – 1 \)
\( \LARGE = (a^2 – 1)(a^4 + a^2 + 1) \)
\( \LARGE =(a-1)(a+1) \)
\( \LARGE \times (a^4 + a^2 + 1) \)
پ) تجزیه به روش اتحاد مکعب دوجملهای
اگر یک چهارجملهای داشته باشیم که دوجمله آن مکعب کامل باشد، حدس میزنیم اتحاد مکعب دوجملهای است. مانند:
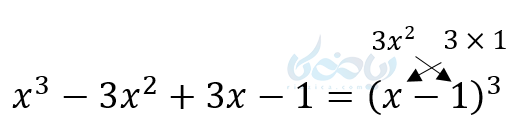
ابتدا مکعب دو جمله مکعب کامل را نوشته و بعد بررسی میکنیم آیا دو جمله دیگر 3 برابر مربع یکی در دیگر هست یا خیر؟
البته از این تجزیه کمتر استفاده میشود و هر چهارجملهای لزوما از این روش تجزیه نمیشود.
3-تجزیه عبارت های جبری به روش دستهبندی و فاکتورگیری
در تجزیه عبارت های جبری ، گاهی در چند جملهایها به خصوص چهارجملهایها، در تمام جملات یک عامل مشترک نداریم و میتوانیم با دستهبندی آنها و فاکتورگیری از این جملات به جملات مشترک برسیم. به مثال زیر دقت کنید:
\( \LARGE a^3 – 2ab + a^{2}b – 2b^2 \)
در اینجا میبینید همگی یک عامل مشترک ندارند ولی دوتا از جملات عامل مشترک \( \Large a^2 \) و دوتا از جملات عامل مشترک \( \Large -2b \) را دارند پس خواهیم داشت:
\( \LARGE a^3 – 2ab + a^{2}b – 2b^2 \)
\( \LARGE = a^2(a+b)-2b(a+b) \)
میبینید که حال دوجملهای \( \Large (a+b) \) عاملمشترک است. پس از این عامل فاکتور میگیریم.
\( \LARGE a^2 – 2ab + a^{2}b – 2b^2 \)
\( \LARGE = a^2(a+b)-2b(a+b) \)
\( \LARGE = (a+b)(a^2 – 2b) \)
مثال:
\( \LARGE 2x^3 – 4x^2 – 6xy + 12y \)
\( \LARGE = 2x(x^2 – 3y) \)
\( \LARGE -4(x^2 – 3y) \)
\( \LARGE = (x^2 – 3y)(2x-4) \)
نکته ۱۲: اگر بعد از فاکتورگیری اولیه دیدید دوجملهایها یکی نیستند، دستهبندی خود را تغییر دهید.
4-روش شکستن و دستهبندی
در تجزیه عبارت های جبری ، گاهی ملاحظه میشود برای تجزیه نمیتوانیم مانند روش دستهبندی و فاکتورگیری عبارت را تجزیه کنیم. اما با شکستن یک یا دو جمله میتوان به روش دستهبندی و فاکتورگیری عبارت را تجزیه کرد.
به مثال زیر دقت کنید:
\( \LARGE 2x^2 + 3x +1 \)
این سهجملهای را در ابتدا نمیتوان دسته بندی کرد ولی میتوانیم با شکستن دو جمله این کار را انجام دهیم. جمله \( \Large 2x^2 , 3x \) را به شکل زیر میشکنیم.
\( \LARGE \rightarrow \begin{cases} 2x^2 = x^2 + x^2 \\ 3x = 2x + x \end{cases} \)
\( \LARGE 2x^2 + 3x +1 \)
\( \LARGE = (x^2 + 2x +1) \)
\( \LARGE +(x^2 + x) \)
\( \LARGE = (x+1)^2+x(x+1) \)
\( \LARGE = (x+1)(x+1+x) \)
\( \LARGE = (x+1)(2x+1) \)
به مثال دیگری در این زمینه دقت کنید که در آن فقط یک جمله را میشکنیم و به صورت تفریق دو جمله مینویسیم.
\( \LARGE 3x^2 + x – 4 \)
\( \LARGE = 3x^2 + 4x – 3x – 4 \)
\( \LARGE = (3x^2-3x) \)
\( \LARGE +(4x-4) \)
\( \LARGE = 3x(x-1)+4(x-1) \)
\( \LARGE = (x-1)(3x+4) \)
البته این نمونهها را میتوانید از روش \( \Large A \) که در تجزیه اتحاد جمله مشترک که به آن اشاره کردیم نیز استفاده کنید.
نکته ۱۳: این دو روش آخر در کتاب درسی و در حد یک مثال آمده است و بیشتر تمرکز کتاب بر روی تجزیه به روش فاکتورگیری و اتحاد است.
ویدیویی از آموزش تجزیه عبارت های جبری
در این ویدیو چند مثال از روش دسته بندی وفاکتور گیری و همین طور روش شکستن ودسته بندی از تجزیه عبارت های جبری برای شما آورده ایم.
زنگ آخر کلاس تجزیه عبارت های جبری
دوستان با هم در ریاضیکا مبحث تجزیه عبارت های جبری را همراه با بیش از ۲۰ مثال گوناگون یادگرفتیم. اگر علاقمند به مطالعه درس شیرین اتحادها نیز هستید، آن را نیز برای شما در بخش آموزش ریاضی دهم قرار دادهایم.
سوالهایتان را زیر همین نوشتار در بخش دیدگاهها بنویسید.. کارشناسان ریاضیکا به سوالهایتان پاسخ میدهند.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!





عالی بود??????
سلام و عرض ادب
متشکرم از توجهی که داشتید.
موفق باشبد.
b + 2bc = چی میشه جوابش
سلام و عرض ادب
می توان در اینجا از b فاکتور گرفت:
(b(1+2c
موفق باشید.
سلام لطفا جواب این سوال حقیر رو بدهید 6x^2-13x-5
یا سلام
به روش A که در پست توضیح دادیم عمل کنید در عدد شش ضرب کنید واز راه جمله مشترک تجزیه کنید سپس به اندازه ۶تا فاکتور بگیریدجواب میشود )(2X-5)(3X+1)
سلام. خواهش میکنم هر چه زودتر به سوالم جواب بدید لطفا
سوال گفته حاصل این عبارت رو با اتحاد ها بدست بیاورید
547 به توان 2+ 500 به توان 2 _(منهای) 47 به توان 2
خواهش میکنم جواب بدید
با سلام
کافیه ۵۴۷ به توان دو را باز کنید بنویسید2^(۵۰۰+۴۷) اگر از اتحاد مربع دو جمله ای استفاده کنیم با بقیه جملات ساده کنیم در نهایت داریم 547000
3a²-4a+2ab-b²+1 رو میشه تجزیه کنید.ممنون میشم
با سلام وعرض ادب
کافیه 3a^2 vرو به 4a^2,a^2 بشکنید دو تا اتحاد مربع دو جمله ای به وجود میاید سپس با اتحاد مزدوج داریم(3a+b-1)(a-b-1)
سلام میشه لطفاروش تجزیه عبارت جبری زیر رو هم بفرمایید
X^3-3x-2
سلام خیلی ممنون از مطلبتون
چطور باید این رو تجزیه کرد؟
(x^3 – 7x^2 + 6x)
با سلام وعرض ادب
کافیست از x فاکتور بگیرید وبعد از راه جمله مشترک تجزیه کنید
خیلی خوب یاد گرفتم ممنونم
اجرتون با آقا امام زمان
باسلام وعرض ادب
ممنون از دعای خیر شما
خیلی ممنون فقط این سوال فک کنم تجزیه نمیشه درسته ؟ x^3-3x^2y+3xy^2+y^3
با سلام و عرض ادب
یا این علامت ها تجزیه نمی شوند ولی اگر همه مثبت یا منفی باشد از راه اتحاد مکعب دو جمله ای تجزیه می شود.
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام شما سایتی برای فیزیک دهم هم دارید یا سایتی پیشنهادی دارید که این سایته شما باشه
سلام و عرض ادب
سایتی متاسفانه نمیشناسیم
دمتون گرم عالی بود???
با سلام واحترام
خدا رو شکر مفید بوده
سلام مطالبی که گذاشتین خیلی برام مفید بودند ممنون. یک سوال هم داشتم، عبارت16x²+36y²-(6y-4x) ²اگه میشه بگین ممنون
با سلام واحترام
دوست عزیز اینجا قادر به پاسخگویی نیستیم
خیلی استفاده کردم
ممنونم
آن شالله عاقبت به خیر بشین…
با سلام واحترام
ممنون از دعای خیر شما خوشحالیم که مفید واقع شده
باسلام
x^3_x^2+24x_144
میشه توضیح بدید چطور حل میشه
با سلام وعرض ادب تجزیه این عبارت با روش شکستن وفاکتور گیری ممکنه باید x^2 رو به دوجمله 3x^2,-4x^2بشکنید و24xرو به 36x,-12xبشکنید بعد از سه جمله از xفاکتور بگیر و ساز سه جمله دیگه از -4فاکتور بگیرید. درنهایت داریم)x-4)(x^2+3x+36)
خیلی عالی بود ، ممنون
با سلام واحترام
ممنون از نظر لطف شما
ممنون میشم ب سوالم جواب بدین سوال خواسته اینو تجزیه کنیم
ایکس به توان ۴+چهارایکس+چهار-ایگرگ ب توان دو
Xبه توان ۴ به علاوه یک چند میشه؟؟؟
با سلام
به مقدار ایکس بستگی داره
سلام دستتون درد نکنه عالی بود ولی شکستن و دسته بندی خیلی سخته
با سلام وادب
خرسندیم که برای شما مفید بوده
روش سوم سرحالم کرد??
با سلام وادب
ممنون از نگاه زیبای شما
سلام ببخشید جواب این سوال رو میشه بگید لطفا؟
حاصل عبارت زیر را بدست آورده و سپس به ساده ترین صورت بنوسید؟
4x(3x-2)-12x²
ممنون میشم اگه واسم حل کنید.
لطفا جواب این سوال هم بگید???
مقدار عددی عبارت 4b²+1 را به ازای b=3 بدست آورید
۹
خوب عزیزم نگاه داخل صورت 4b²+1بجای bداخل سوال 3میزاریم=1+²(3)4=33
سلام خسته نباشید لطفا این سئوال رو واس من حل کنید
معادله های زیر را حل کنید.
5x=x-12 4x+15=7x+21
سلام لطفا جواب این سوال هرکس بلده با راه حل به منم بگه لطفا???
جاهای خالی را پرکنید؟
6ab+8b²=2b
ببخشید
2ab+8b²c=2b
(………)+(……..)
a=3
b=_2
چون
6ab+8b²=2b
اول تجزیه میکنیم سمت راست را که میشه b(6a+8b)=2b
حالا دو ۲ طرف را بر b تقسیم میکنیم
که میشه 6a+8b=2
و معادله حل میشه که a=3
b=_2
با سلام
ممنون از پایخگویی شما ولی نمیشه دو طرف یه معادله رو به متغیر تقسیم کرد چون یکی از جوابها از دست میره بعد اینکه کلا یه معادله بادومجهول قابل حل نیست منظور سوال این دوستمون اصلا مشخص نیست
سلام
تجزیه عبارت 25y^2+25y+6 چی میشه؟
سلام خوبین پاسخ این تجزیه چی میشه r*3+r*2+r+1
سلام..وقتتون بخیر..از این قسمت تجزیه میشه یه سوال کاربردی وسخت بگید؟ مثلا میشه سوالی طرح کرد که مسئله ای باشه. یا عددی باشه
خواهش میکنم جواب این بنده ی حقیر رو بدید.
آیا برای فاکتور گیری واجب است که بین اعداد ب م م بگیرم؟؟؟؟
یا سلام وادب
نه ذهتی هم میشه فهمید که ضرایب مشترکا به چی بخش پذیرند
خیر
ببخشید این سوال چی میشه ؟؟
x⁴+4x²+16
سلام دوست عزیز
یه ۲x*۲ اضافه وکم کن بعد با تجزیه به روش مربع کامل ومزدوج حل میشه
با سلام
بسیار عالی هستید .
نکته 8 نیاز به ویرایش دارد.
با تشکر
با سلام دوست عزیز
دقیقا کجای مطلب احتیاج به ویرایش دارد
با سلام اگر لطف کنید یه سری نمونه سوال تجزيه ترکیبی و سطح بالا که با روشهایی مثل دسته بندی و شکستن و … بگذارید در قالب پی دی اف ممنونم
با سلام
انشاالله به زودی قرار میدیم
درود خدا بر شما
احسنت
🌺🌺🌺
سلام دوست عزیز
ممنون از نظر لطف شما
سلام ممنونم از مقاله خوب تان در مورد تجزیه عبارات جبری
سلام
\(x^3 + x + 3\)
را چگونه تجزیه کنیم؟