آموزش ریاضی پایه دهم
آموزش دنباله حسابی 🧮🔢 – از همیشه ساده‌تر؟
بهمن
در این پست از مجموعه آموزش‌های ریاضی پایه دهم از سایت ریاضیکا با آموزش دنباله حسابی در خدمت شما دانش‌آموزان هستیم. دنباله حسابی یکی از مهمترین دنباله‌های با الگو در ریاضیات است که به فراوانی در اطراف ما دیده میشود. پس داشتن یک الگوی کلی برای تمام دنباله های حسابی و بررسی آن‌ها مهم است که ما در این نوشتار به آن می‌پردازیم. شما در این مطلب (آموزش دنباله حسابی) به طور قطع به جواب تمامی سوال‌هایتان می‌رسید.
در قسمت قبل با الگوی خطی آشنا شدیم. نام دیگر الگوی خطی دنباله حسابی است که تعریف دقیق آن به صورت زیر است.
تعریف دنباله حسابی
دنباله ای عددی که فاصله هر دو جمله متوالی آن یک مقدار ثابت است که به این مقدار ثابت قدر نسبت می گویند. قدر نسبت را با حرف \( \Large d \) نمایش می‌دهند. قدرنسبت هر عدد حقیقی می‌تواند باشد.
مثال 1: در دنباله های حسابی زیر، جمله اول و قدر نسبت را مشخص کنید؟
حل 1:
(1
\( \LARGE 4 , 7 , 10 , … \)
\( \LARGE \begin{cases} a_1 = 4 \\ d = 3 \end{cases} \)
(2
\( \LARGE -1 , -3 , -5 , … \)
\( \LARGE \begin{cases} a_1 = -1 \\ d = -2 \end{cases} \)
(3
\( \LARGE 1 , 1\frac{1}{2} , 2 , 2\frac{1}{2} , 3 , … \)
\( \LARGE \begin{cases} a_1 = 1 \\ d = \frac{1}{2} \end{cases} \)
(4
\( \LARGE 5 , 5 , 5 , … \)
\( \LARGE \begin{cases} a_1 = 5 \\ d = 0 \end{cases} \)
(5
\( \LARGE \sqrt2 , 2\sqrt2 , 3\sqrt2 , … \)
\( \LARGE \begin{cases} a_1 = \sqrt2 \\ d = \sqrt2 \end{cases} \)
همانطور که مشاهده می‌کنید قدر نسبت می‌تواند مثبت، منفی، عدد گویا و حتی صفر باشد.
نکته ۱: اگر \( \Large d \) مقداری مثبت باشد، دنباله صعودی و اگر \( \Large d \) مقداری منفی باشد، دنبال نزولی است. اگر \( \Large d = 0 \) باشد، دنباله ثابت خواهد بود. پس برای هر دنباله سه حالت وجود دارد:
- صعودی: قدر نسبت مثبت
- نزولی: قدر نسبت منفی
- ثابت: قدر نسبت صفر
نکته ۲: در دنباله هایی با قدر نسبت مساوی این جمله اول است که باعث میشود دنباله ها یکسان نباشند. پس در یک دنباله حسابی هم جمله اول و هم قدر نسبت دارای اهمیت هستند.
در این دو دنباله جمله‌های اول یکسان اما قدر نسبتها متفاوت است.
\( \LARGE 5 , 2 , -1 , -4 , … \)
\( \LARGE \begin{cases} a_1 = 5 \\ d = -3 \end{cases} \)
\( \LARGE 5 , 8 , 11 , 14 , … \)
\( \LARGE \begin{cases} a_1 = 5 \\ d = 3 \end{cases} \)
در این دو دنباله حسابی، قدر نسبتها مساوی، ولی جملات اول یکسان نیستند.
\( \LARGE 2 , 4 , 6 , 8 , … \)
\( \LARGE \begin{cases} a_1 = 2 \\ d = 2 \end{cases} \)
\( \LARGE 1 , 3 , 5 , 7 , … \)
\( \LARGE \begin{cases} a_1 = 1 \\ d = 2 \end{cases} \)
تشخیص دنباله حسابی
یکی از نکات مهم در آموزش دنباله حسابی ، تشخیص این دنباله از بین دنباله های داده شده است. برای تشخیص دادن یک دنباله حسابی کافیست دو جفت جمله متوالی را از هم کم کنیم اگر مقداری ثابت شد دنباله حسابی است.
مثال 2: آیا دنباله های زیر حسابی هستند؟
حل 2:
(1
\( \LARGE \frac{5}{3} , \frac{7}{6} , \frac{2}{3} , … \)
\( \LARGE \begin{cases} a_2 – a_1 = \frac{7}{6} – \frac{5}{3} = -\frac{1}{2} \\ a_3 – a_2 = \frac{2}{3} – \frac{7}{6} = -\frac{1}{2} \end{cases} \)
دنباله حسابی است.
(2
\( \LARGE \frac{1}{2} , \frac{1}{4} , \frac{1}{6} , … \)
\( \LARGE \begin{cases} a_2 – a_1 = \frac{1}{4} – \frac{1}{2} = -\frac{1}{4} \\ a_3 – a_2 = \frac{1}{6} – \frac{1}{4} = -\frac{1}{12} \end{cases} \)
دنباله حسابی نیست.
فرمول جمله عمومی دنباله حسابی
فرض کنید، \( \Large a_1 , a_2 , a_3 , … \) جملات متوالی یک دنباله حسابی باشند. پس می‌دانیم:
\( \LARGE \begin{cases} 1) a_2 = a_1 + d \\ 2) a_3 = a_2 + d \end{cases} \)
از رابطه 1 و 2 به رابطه زیر میرسیم:
\( \LARGE a_3 = a_1 + 2d \)
پس به طور کلی داریم:
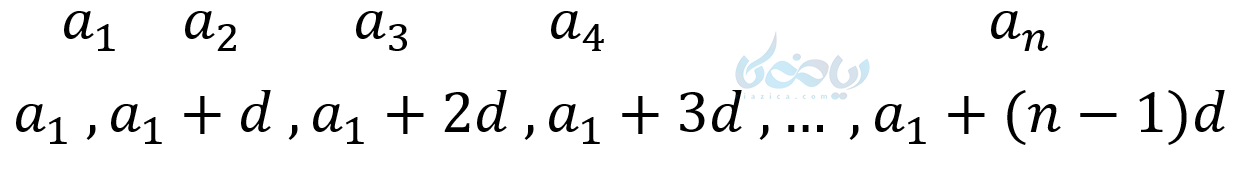
با توجه به جملات دنباله نتیجه می‌گیریم برای پیدا کردن جمله عمومی یک دنباله حسابی به جمله اول و قدر نسبت نیاز داریم تا با قرار دادن آن‌ها در رابطه زیر فرمول جمله عمومی به دست آید:
مثال 3: جمله عمومی دنباله حسابی زیر را بنویسید؟
\( \LARGE -7 , -4 , -1 , … \)
حل 3:
\( \LARGE -7 , -4 , -1 , … \)
\( \LARGE \begin{cases} d = -4 – (-7) = 3 \\ a_1 = -7 \\ a_n = ? \end{cases} \)
\( \LARGE a_n = a_1 + (n – 1) d \)
\( \LARGE a_n = -7 + (n – 1) \times 3 \)
پس از مرتب کردن داریم:
\( \LARGE a_n = 3n – 10 \)
پس با رابطه ای که برای جمله عمومی بدست آوردیم به راحتی جمله عمومی و یا جملات دیگر دنباله حسابی را می‌توانیم بدست آوریم.
مثال 4: در دنباله حسابی زیر جمله بیستم را بدست آورید.
\( \LARGE 3 , 1 , -1 , … \)
حل 4:
\( \LARGE 3 , 1 , -1 , … \)
\( \LARGE \begin{cases} d = 1 – 3 = -2 \\ a_1 = 3 \\ a_{20} = ? \end{cases} \)
\( \LARGE n = 20 \)
\( \LARGE \rightarrow a_{20} = a_1 + 19d \)
\( \LARGE \rightarrow a_{20} = 3 + 19 \times (-2) \)
\( \LARGE \rightarrow a_{20} = -35 \)
پس جمله 20ام عدد 35- است.
مثال 5: جمله چندم دنباله حسابی زیر 12 است؟
\( \LARGE 3 , \frac{10}{3} , \frac{11}{3} , … \)
حل 5:
\( \LARGE 3 , \frac{10}{3} , \frac{11}{3} , … \)
\( \LARGE \begin{cases} d = \frac{11}{3} – \frac{10}{3} = \frac{1}{3} \\ a_1 = 3 \\ a_n = 12 \rightarrow n = ? \end{cases} \)
\( \LARGE a_n = a_1 + (n – 1) d \)
\( \LARGE 12 = 3 + (n – 1) \times \frac{1}{3} \)
پس از مرتب کردن داریم:
\( \LARGE \frac{n}{3} = \frac{28}{3} \rightarrow n = 28 \)
مثال 6: در یک دنباله حسابی جمله چهارم 25 ، و جمله دهم 67 است. این دنباله را مشخص کنید.
حل 6:
\( \LARGE \begin{cases} a_4 = 25 \\ a_{10} = 67 \end{cases} \)
\( \LARGE \rightarrow \begin{cases} a_4 = a_1 + 3d = 25 \\ a_{10} = a_1 + 9d =67 \end{cases} \)
حل دستگاه:
\( \LARGE \begin{cases} a_1 = 4 \\ d = 7 \end{cases} \)
پس دنباله را به صورت زیر می‌نویسیم:
\( \LARGE 4 , 11 , 18 , 25 \)
نکته ۳: برای حل مثال‌هایی مانند مثال بالا که دو جملهٔ یک دنباله حسابی داده شده و قدر نسبت و جمله اول را می‌خواهیم، می‌توانیم از رابطهٔ زیر که در اصل از ساده کردن همان دستگاه بالا به دست می‌آید استفاده کنیم:
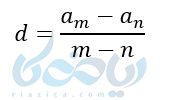
که در آن \( \Large m , n \) شماره جملات دنباله و \( \Large a_m , a_n \) جملات داده شده هستند. به شکلی که \( \Large m > n \) است.
لازم است به این نکته توجه کنیم که بعد از بدست آوردن \( \Large d \)، باید با استفاده از رابطه ی یکی از جملات داده شده \( \LARGE a_1 \) را به دست آوریم.
مثال 7: جملهٔ پنجم یک دنباله 11- و جملهٔ یازدهم آن 47- است. این دنباله را مشخص کنید.
حل 7:
\( \LARGE \begin{cases} a_5 = -11 \\ a_{11} = -47 \end{cases} \)
\( \LARGE d = \frac{a_m – a_n}{m – n} \)
\( \LARGE \rightarrow d = \frac{-47 – (-11)}{11 – 5} = -6 \)
\( \LARGE a_5 = -11 \)
\( \LARGE \rightarrow a_{5} = a_1 + 4d \)
\( \LARGE -11 = a_1 +4 \times (-6) \)
\( \LARGE \rightarrow a_1 = 13 \)
\( \LARGE \begin{cases} a_1 = 13 \\ d = -6 \end{cases} \)
\( \LARGE a_n = a_1 + (n – 1)d \)
\( \LARGE a_n = -6n + 19 \)
نکته ۴: اگر بین دو عدد \( \Large a \) و \( \Large b \) چند عدد را طوری درج کنیم که همگی تشکیل دنباله حسابی دهند، می‌گوییم این اعداد واسطه حسابی هستند.
مثال ۸: جمع سه جمله اول یک دنباله حسابی برابر با ۳ است. جمع سه جمله دوم آن نیز برابر با ۳۹ میباشد. این دنباله را مشخص کنید. (تمرین ۳ صفحه ۲۴ کتاب ریاضی دهم)
حل ۸:
مثال ۹: بین دو عدد ۱۸ و 62 سه واسطه حسابی درج کنید.
حل ۹:
راه اول:
\( \LARGE 18 , … , … , … , 62 \)
\( \LARGE a_1 = 18 \)
\( \LARGE a_5 = 62 \)
\( \LARGE \rightarrow a_{5} = a_1 + 4d \)
\( \LARGE 62 = 18 + 4d \)
\( \LARGE \rightarrow d = \frac{62 – 18}{4} = \frac{44}{4} = 11 \)
\( \LARGE \begin{cases} a_1 = 18 \\ d = 11 \end{cases} \)
پس داریم:
\( \LARGE 18 , 29 , 40 , 51 , 62 \)
راه دوم:
از رابطه
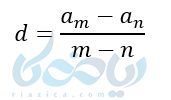
استفاده کنیم.
\( \LARGE 18 , … , … , … , 62 \)
\( \LARGE a_1 = 18 \)
\( \LARGE a_n = a_1 , a_m = a_5 \)
\( \LARGE d = \frac{a_m – a_n}{m – n} \)
\( \LARGE \rightarrow d = \frac{62 – 18}{4} = \frac{44}{4} = 11 \)
\( \LARGE \begin{cases} a_1 = 18 \\ d = 11 \end{cases} \)
پس داریم:
\( \LARGE 18 , 29 , 40 , 51 , 62 \)
نوشتن واسطه حسابی با آموزش دنباله حسابی
نکته ۵: اگر \( \Large a , b , c \) سه جملهٔ متوالی یک دنباله حسابی باشند، آنگاه داریم:
\( \LARGE \begin{cases} b – a = d \\ c – b = d \end{cases} \)
\( \LARGE \rightarrow b – a = c – d \)
\( \LARGE \rightarrow 2b = a + c \)
\( \LARGE \rightarrow b = \frac{a + c}{2} \)
یعنی در سه جملهٔ متوالی یک دنباله حسابی، جملهٔ وسطی میانگین جملهٔ اول و سوم است و به آن واسطه حسابی می‌گویند.
مثال ۱۰: مقدار \( \Large x \) را چنان بیابید که سه جملهٔ زیر جملات متوالی یک دنباله حسابی باشند.
\( \LARGE 4x – 1 , x + 2 , 2 – x \)
حل ۱۰:
\( \LARGE \begin{cases} a = 4x – 1 \\ b = x +2 \\ c = 2 – x \end{cases} \)
\( \LARGE b = \frac{a + c}{2} \)
\( \LARGE x + 2 = \frac{4x – 1 + 2 -x}{2} \)
\( \LARGE 2x + 4 = 3x + 1 \)
\( \LARGE \rightarrow x = 3 \)
اگر \( \Large x \) را جایگذاری کنیم، داریم:
\( \LARGE 11 , 5 , -1 \)
سوالات شما در آموزش دنباله حسابی
مثال ۱۱: در الگوی خطی جملات دوم و پنجم قرینه هم هستند و جمله هفتم برابر 7 میباشد. الگوی عمومی رابیابید.
حل ۱۱:
\( \LARGE \begin{cases} a_2 = -a_5 \\ a_7 = 7 \end{cases} \)
\( \LARGE a_2=-a_5 \)
\( \LARGE a+d=-(a+4d) \)
\( \LARGE a+d=-a-4d \)
\( \LARGE 2a=-5d \rightarrow a=-2.5d \)
\( \LARGE a_7 = 7 \)
\( \LARGE a+6d = 7 \rightarrow a=-2.5d \)
\( \LARGE -2.5d+6d=7 \rightarrow d=2\)
\( \LARGE \begin{cases} d=2\\ a=-5 \end{cases} \)
\( \LARGE a_n =a +(n-1)d \) \( \LARGE a_n =2n-7 \)
دو نکتهٔ مهم مشاوره‌ای از آموزش دنباله حسابی
نکته ۶: دقت کنید با دانستن آموزش دنباله حسابی ، تعریف دنباله حسابی و رابطهٔ جملهٔ عمومی دنباله حسابی بدون احتیاج به هیچ کدام از رابطه های دیگر می‌توان به تمام سوالات این قسمت جواب دهیم.
نکته ۷: قبل از آن که در یک موضوع ریاضی به دنبال حل مسائل بیشتر و تست زدن باشیم، باید ابتدا مفهوم اصلی را به خوبی درک کنیم و مسائل ساده را چندین بار و با مثال‌های متعدد حل کنیم. سپس به مسائل پیچیده‌تر و تست زدن بپردازیم.
آخر کلاس امروز آموزش دنباله حسابی
آموزش دنباله حسابی یکی از بخش‌های مهم در ریاضی پایه دهم است. ما در این نوشتار با مثال‌های خیلی زیادی این مبحث رو باهم یادگرفتیم. با سه نوع صعودی، نزولی و ثابت آشنا شدیم و تونستیم باهم دنباله‌های مختلفی رو تشخیص بدهیم. همچنین یاد گرفتیم که قدر نسبت و جمله اول یه دنباله رو حساب کنیم.
اگر بعد از مطالعه این نوشتار هر سوالی به ذهنتون رسید، می‌تونید تو بخش دیدگاه‌ها در پایین همین قسمت از ما سوالتون رو بپرسید. ما در ریاضیکا اینجاییم تا به سوالات شما پاسخ بدیم.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی دهم به شما پیشنهاد می‌دهیم:
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- آموزش دنباله حسابی 🧮🔢 – از همیشه ساده‌تر؟
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش حل نامعادله همراه با رسم نمودار و مثال‌های متنوع↪️📝
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع خطی به سادگی یک خط مستقیم 📈📏
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!
خوب بود ممنون
ممنون از شما دوست گرانقدر
عالیهههههههههههههه
واقعا قابل تحسین امیدوارم زندگی نویسنده مثل توضیح و مثال هاش باکیفیت بمونه
سلام دوست عزیز
ممنون از انرژی که به ما دادید.
موفق و پیروز باشید.
عالی بودخیلی ممنونم❤❤ خسته نباشید ??
سلام و عرض ادب
متشکرم از توجهی که داشتید.
موفق باشبد.
کارتون عالیه خسته نباشید. ممنون از این جمع بندیه عالی
سلام و عرض ادب
ممنون از انرژی و پیام پرمهرتون.
موفق باشید
سلام در آخرین مثال، مثال 11؛ اون a چطوری منفی 5 شد ؟ و ممنون میشم ک توضیح بدید جمله عمومیشو چطوری بدست آوردید.
با سلام واحترم
a اشتباه محاسبه شده بود تصحیح شد
سلام یه سوال دارم اگر قدر نسبت دنباله حسابی
مثلا tn=dn+1 را دو برابر کنیم جمله پانزدهم چند برابر میشود؟
واقعا ممنون ازسایت خوبتون خیلی مطالب مفید و واضح اند،من با این مطالب خیلی از تستارو میتونم جواب بدم واقعا ممنون❤❤❤
با سلام
ما نتیجه سی سال تدریس رو در سایتمون گذاشتیم
خیلی عالییییییییی بود پایدار وموفق باشید
با سلام وادب
ممنون از دعای خیر شما
با سلام و خسته نباشید. اگر امکان دارد این سوال را جواب دهید.
سه عدد متوالی در دنباله حسابی تشکیل مثلث قائم الزاویه به محیط 24 را می دهد. این سه عدد را بیابید.
با سلام و خسته نباشید. اگر امکان دارد این سوال را برای من جواب دهید.
سه عدد متوالی در دنباله حسابی تشکیل مثلث قائم الزاویه ای به محیط 24 را می دهد،این سه عدد را بیابید.
با سلام دوست عزیز
کافیه این سه جمله رو بر حسب جمله اول وقدر نسبت بنویسی یه بار جمع کنی مساوی۲۴ پس از ساده سازی مجموع جمله اول وقدر نسبت میشود ۸ a+d=8 طبق رابظطه فیثاغورس هم به دست میاد 3d-a=0 بعد حل دستگاه به اعداد ۶و۸ و۱۰ میرسیم
با سلام.
من در سه سال اخیر به خاطر کرونا رابطه ی فیثاغورس و حل دستگاه را درست یاد نگرفتم. اگر امکان دارد جواب را کامل برام بفرستید. ممنونم از استاد بزرگوار. اجرتان با خدا.
سلام دوست عزیز
اینجا امکانش نیست
باید سعی کنید این دروس رو یاد بگیرید چون پایه ای هستن
با سلام
هیچ سایتی به این سادگی با زبان ساده بیان نکرده ممنون از وقتی که گذاشتید
سلام
سپاسگزارم
بسیار جامع و ساده و روان و قابل فهم بیان شده
من برای آموزش به دخترم همیشه از مطالب این سایت استفاده میکنم
سلام
ممنون از نگاه شما