آموزش ریاضی پایه دهم
آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
آموزش رسم سهمی و رسم نمودار معادلات و توابع (که در فصل بعدی از کتاب آموزش ریاضی دهم با آنها آشنا میشویم) در ریاضیات بسیار حائز اهمیت است. زیرا ما با استفاده از نمودار یک معادله به سوالات زیادی میتوانیم پاسخ دهیم و حتی ریشههای آن را پیدا کنیم. همینطور به تابع بودن یا نبودن آن را پی میبریم. قبلاً دیدیم که نمودار معادلات درجه اول به صورت یک خط راست است. در مبحث آموزش رسم سهمی باهم یاد خواهیم گرفت که نمودار معادلات درجه دوم، یک منحنی به نام سهمی میشود.
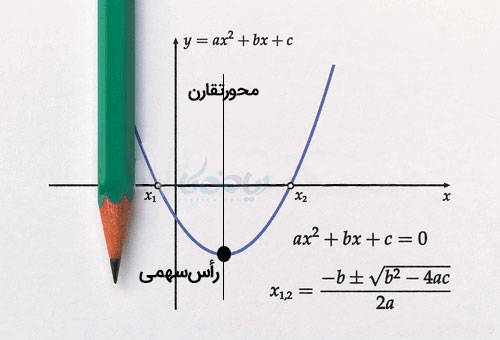
رسم نمودار معادله درجه دوم ساده \( \LARGE y = x^2 \)
از نکات مهم و سادهای که در آموزش رسم سهمی یاد میگیریم این است یکی از سادهترین روشهای رسم نمودار هر معادله و تابعی نقطهیابی است. یعنی به \( \Large x \) مقدار داده و مقادیر \( \Large y \) را پیدا میکنیم. به جدول زیر دقت کنید.
| … | 2 | 1 | \( \Large \frac{1}{2} \) | 0 | \( \Large \frac{-1}{2} \) | -1 | -2 | x |
|---|---|---|---|---|---|---|---|---|
| … | 4 | 1 | \( \Large \frac{1}{4} \) | 0 | \( \Large \frac{1}{4} \) | 1 | 4 | y |
اگر این نقاط را روی محور مختصات پیدا میکنیم نمودار این معادله یک منحنی خواهد شد که آن را سهمی مینامیم.
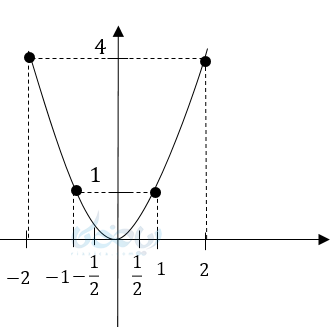
در این سهمی، مبدأ را راس سهمی میگویند. دهانه سهمی رو به بالا است و محور عرضها محور تقارن این نمودار خواهد بود. در اینجا \( \Large a \) یعنی ضریب \( \Large x^2 \) مثبت است. در ادامه میخواهیم قرینه معادله بالا را رسم کنیم.
رسم نمودار معادله درجه دوم ساده \( \LARGE y = -x^2 \)
| … | 2 | 1 | \( \Large \frac{1}{2} \) | 0 | \( \Large \frac{-1}{2} \) | -1 | -2 | x |
|---|---|---|---|---|---|---|---|---|
| … | -4 | -1 | \( \Large \frac{-1}{4} \) | 0 | \( \Large \frac{-1}{4} \) | -1 | -4 | y |
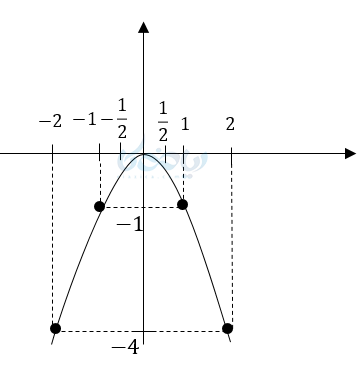
در مبحث آموزش رسم سهمی میبینیم مبدأ رأس سهمی است. ولی دهانهٔ سهمی رو به پایین و باز محور عرضها محور تقارن نمودار است. در اینجا \( \Large a \) بعنی ضریب \( \Large x^2 \) منفی است.
پس به طور کلی نمودار هر معادله \( \Large y = ax^2 + bx + c \) که در آن \( \Large a , b , c \) اعداد حقیقی هستند و \( \Large a \neq 0 \) یک سهمی میشود. توجه به سه مورد زیر بسیار مهم و ضروری است:
- اگر \( \Large a > 0 \) باشد نمودار ∪ و راس سهمی پایینترین نقطه نمودار است.
- اگر \( \Large a < 0 \) باشد نمودار ∩ میباشد و راس بالاترین نقطه نمودار است.
- همچنین خط عمودی که از رأس سهمی میگذرد محور تقارن سهمی نامیده میشود.
حال این سوال پیش میآید که ما هر بار برای رسم نمودار یک معادله درجه دوم باید این همه نقاط پیدا کنیم و راه سادهتری وجود ندارد؟ بله، وجود دارد. در قسمت پایین از آموزش رسم سهمی میتوانید ببینید:
روشهای رسم نمودار معادله درجه دوم
در آموزش رسم سهمی میآموزیم که به طور کلی میتوان دو روش مختلف را برای رسم نمودار معادله درجه دوم به کار برد:
- روش مربع کامل برای رسم نمودار معادله درجه دوم
- پیدا کردن راس از رابطه \( \LARGE (-\frac{b}{2a},-\frac{\Delta}{4a}) \)
1- روش مربع کامل برای رسم نمودار معادله درجه دوم
ابتدا باید توضیح دهیم معادلات درجه دوم به دو فرم نوشته میشوند:
- فرم گسترده
\( \LARGE y = ax^2 + bx + c \)
\( \LARGE a \neq 0 \)
- فرم تجزیه شده یا مربع کامل
\( \LARGE y = a(x-h)^2 + k \)
\( \LARGE a \neq 0 \)
اگر معادله داده شده برای رسم نمودار به فرم تجزیه شده یا همان مربع کامل باشد، کار برای ما راحتتر است. ابتدا رأس را که برابر است با
\( \Large (h , k) \) پیدا کرده و در وسط جدول نوشته و با دو نقطه کمکی دیگر که معمولاً یک واحد قبل و بعد \( \Large h \) را برای \( \Large x \) در نظر گرفته، پیدا میکنیم. خط \( \Large x = h \) محور تقارن است.
به مثال زیر دقت کنید.
مثال ۱: نمودار معادله مقابل را رسم کنید؟ \( \LARGE y = (x+1)^2 – 3 \)
حل ۱:
| \( \Large 0 \) | -1 | -2 | x |
|---|---|---|---|
| -2 | -3 | -2 | y |
راس سهمی \( \LARGE S:(-1,-3) \)
دهانه رو به بالا \( \LARGE a>0 \)
محور تقارن \( \LARGE x=-1 \)
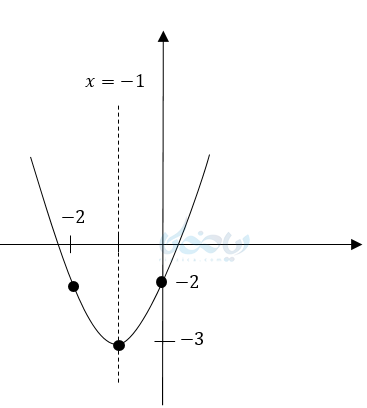
در واقع ما رأس و دو نقطه متقارن با آن را پیدا کرده و به راحتی نمودار را رسم میکنیم. در این مثال \( \Large S:(-1,-3) \) و چون \( \Large a > 0 \) است نمودار رو به بالا است. همچنین خط \( \Large x = -1 \) محور تقارن نمودار خواهد بود.
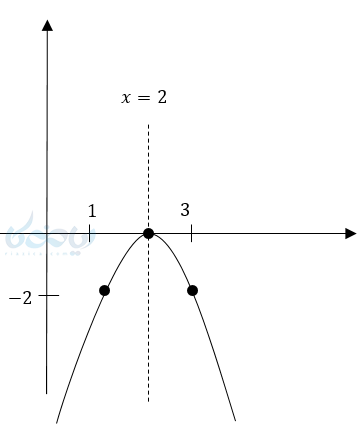
مثال ۲: نمودار تابع روبرو را رسم کنید؟ \( \LARGE y = -(x-2)^2 \)
حل ۲:
| 3 | 2 | 1 | x |
|---|---|---|---|
| -1 | \( \Large 0 \) | -1 | y |
راس سهمی \( \LARGE S:(2,0) \)
دهانه رو به پایین \( \LARGE a<0 \)
محور تقارن \( \LARGE x=2 \)
اما اگر معادله درجه دوم ما به فرم گسترده \( \Large y = ax^2 + bx + c \) باشد، ابتدا آن را به فرم تجزیه شده یا همان مربع کامل در میآوریم. اجازه دهید با یک مثال ابتدا موضوع را مطرح میکنم.
مثال ۳: نمودار تابع \( \Large y = x^2 -2x + 3 \) را رسم کنید؟
حل ۳:
همانطور که در روش مربع کامل در حل معادلات درجه دوم گفتیم برای اینکه این معادله به صورت مربع کامل شود، نباید \( \Large x^2 \) ضریب غیر از یک داشته باشد. سپس ضریب \( \Large x \) را نصف و به توان دو میرسانیم. عدد به دست آمده را اضافه و کم میکنیم. در واقع ما به اندازه صفر اضافه کردهایم ولی این کار به تجزیه معادله کمک میکند. یعنی:
\( \LARGE y = x^2 -2x + 3 \)
\( \LARGE y = (x^2 -2x+1)-1+3 \)
\( \LARGE y = (x-1)^2 + 2 \)
حال به همان روش که در بالا گفتیم نمودار را رسم میکنیم.
| 2 | 1 | \( \Large 0 \) | x |
|---|---|---|---|
| 3 | 2 | 3 | y |
رأس سهمی \( \LARGE S:(1,2) \)
دهانه رو به بالا \( \LARGE a>0 \)
محور تقارن \( \LARGE x=1 \)
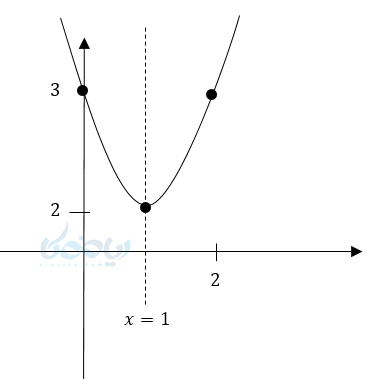
نکته ۱ آموزش رسم سهمی: نقاط کمکی برای بهتر رسم کردن است و گرنه با همان راس و اطلاعات بدست آمده به راحتی نمودار رسم میشود.
مثال ۴: نمودار تابع \( \Large y = -x^2 + x \) را رسم کنید؟
حل ۴:
در این مثال ابتدا از منفی فاکتور میگیریم، سپس تجزیه میکنیم.
\( \LARGE y = -(x^2 – x) \)
\( \LARGE y = -(x^2 – x + \frac{1}{4} – \frac{1}{4}) \)
\( \LARGE y = -(x – \frac{1}{2})^2 + \frac{1}{4} \)
در این مثال برای پیدا کردن نقطههای کمکی، برای راحتتر کردن کار، میتوانیم نیم واحد قبل و بعد را در نظر بگیریم.
| \( \Large 1 \) | \( \LARGE \frac{1}{2} \) | \( \Large 0 \) | x |
|---|---|---|---|
| \( \Large 0 \) | \( \LARGE \frac{1}{4} \) | \( \Large 0 \) | y |
رأس سهمی \( \LARGE S:(\frac{1}{2},\frac{1}{4}) \)
دهانه رو به پایین \( \LARGE a<0 \)
محور تقارن \( \LARGE x=\frac{1}{2} \)
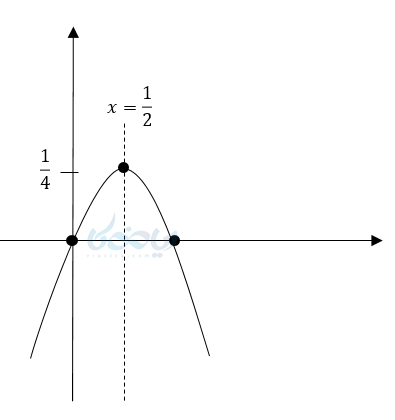
مثال ۵: نمودار \( \Large y = 3x^2 – 6x + 1 \) را رسم کنید؟
حل ۵:
در این مثال نیز چون \( \Large x^2 \) ضریب دارد، ابتدا از 3 فاکتور میگیریم و سپس تجزیه میکنیم.
\( \LARGE y = 3(x^2 – 2x + \frac{1}{3}) \)
\( \LARGE y = 3(x^2 – 2x + 1 – 1 + \frac{1}{3}) \)
\( \LARGE y = 3(x-1)^2 – 2 \)
| \( \LARGE 2 \) | \( \LARGE 1 \) | \( \Large 0 \) | x |
|---|---|---|---|
| \( \LARGE 1 \) | \( \LARGE -2 \) | \( \LARGE 1 \) | y |
رأس سهمی \( \LARGE S:(1, -2) \)
دهانه رو به بالا \( \LARGE a>0 \)
محور تقارن \( \LARGE x=1 \)
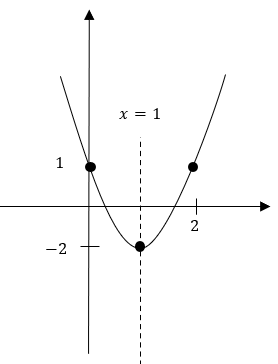
نکته ۲ آموزش رسم سهمی: وقتی \( \Large a \) عدد بزرگتر از 1 یا کوچکتر از 1- باشد دهانه سهمی بستهتر میشود.
نکته ۳ آموزش رسم سهمی: وقتی \( \Large a \) عدد بین 0 و 1 باشد یا بین 0 و 1- دهانه سهمی بازتر میشود.
2- پیدا کردن راس از رابطه \( \LARGE (-\frac{b}{2a},-\frac{\Delta}{4a}) \)
اگر معادله درجه دوم به فرم گسترده را بخواهیم به فرم مربع کامل بنویسیم خواهیم داشت:
\( \LARGE y = ax^2 + bx +c \)
\( \LARGE y = a(x^2 + \frac{b}{a}x +\frac{c}{a}) \)
\( \LARGE y = a(x^2 + \frac{b}{a}x + \frac{b^2 }{4a^2} \)
\( \LARGE – \frac{b^2 }{4a^2}+\frac{c}{a}) \)
\( \LARGE y = a(x + \frac{b}{2a} )^2 \)
\( \LARGE + \frac{4ac-b^2 }{4a} \)
خب در این رابطه \( \LARGE h = – \frac{b}{2a} \) و \( \LARGE k = \frac{4ac-b^2}{4a}= – \frac{\Delta}{4a} \) خواهند بود.
یعنی راس سهمی برابر است با: \( \LARGE S : (-\frac{b}{2a},-\frac{\Delta}{4a}) \)
خب از این پس وقتی معادله درجه دومی را بخواهیم رسم کنیم که به فرم گسترده داده شده بود، دیگر نیازی به مربع کامل کردن آن نیست. ما میتوانیم از روابط بالا برای پیدا کردن رأس سهمی استفاده میکنیم.
نکته ۴: آموزش رسم سهمی میگوید، شما با داشتن رابطه \( \LARGE x_s = – \frac{b}{2a} \) به تنهایی نیز میتوانید نمودار معادله درجه دوم را رسم کنید. وقتی \( \Large x_s \) یعنی طول رأس را پیدا کردید با جایگذاری آن در معادله \( \Large y \) رأس را نیز میتوانید به سادگی پیدا کنید.
مثال ۶: نمودار تابع \( \Large y = x^2 + 4x +1 \) را رسم کنید؟
حل ۶:
\( \LARGE x_s = -\frac{b}{2a} =-\frac{4}{2}=-2 \)
جایگذاری در معادله:
\( \LARGE y_s = (-2)^2 + 4(-2) +1 \)
\( \LARGE y_s = -3 \)
| -1 | -2 | -3 | x |
|---|---|---|---|
| -2 | -3 | -2 | y |
رأس سهمی \( \LARGE S:(-2,-3) \)
دهانه رو به بالا \( \LARGE a>0 \)
محور تقارن \( \LARGE x=-2 \)
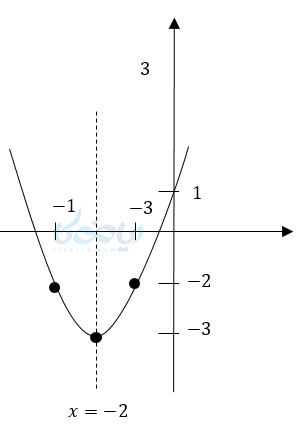
مثال ۷: نمودار معادله \( \Large y = 3x^2 – 2 \) را رسم کنید؟
حل ۷:
\( \LARGE x_s = -\frac{b}{2a} =\frac{0}{6}=0 \)
جایگذاری در معادله:
\( \LARGE y_s = 3(0)^2 – 2=-2 \)
| 1 | \( \Large 0 \) | -1 | x |
|---|---|---|---|
| 1 | -2 | 1 | y |
رأس سهمی \( \LARGE S:(0,-2) \)
دهانه رو به بالا \( \LARGE a>0 \)
محور تقارن \( \LARGE x=0 \)
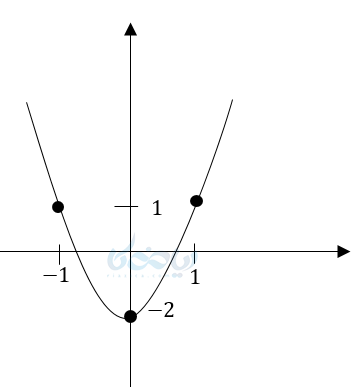
مثال ۸: نمودار یک سهمی محور \( \Large y \)ها را در نقطهای به عرض 2 و محور \( \Large x \)ها را در نقاط 1- و 2 قطع کرده است معادله این سهی را بنویسید و آن را رسم کنید؟
حل ۸:
میدانیم معادله سهمی یا همان معادله درجه دوم برابر است با:
\( \LARGE y = ax^2 + bx + c , (1) \)
در این تمرین در واقع به سه نقطه یا سه مقدار برای \( \Large x , y \) داده شده است با فرار دادن این سه نقطه در معادله ضرایب a,b,c را بدست می اوریم. یعنی داریم:
\( \LARGE (0,2) \)
\( \LARGE \rightarrow 2 = a(0)^2 + b(0) + c \)
\( \LARGE \rightarrow c = 2 \)
حال به جای \( \Large c \) عدد 2 قرار میدهیم.
\( \LARGE (2,0) \)
\( \LARGE 0 = a(2)^2 + b(2) + 2 \)
\( \LARGE \rightarrow 4a+2b=-2 \)
\( \LARGE (-1,0) \)
\( \LARGE 0 = a(-1)^2 + b(-1) + 2 \)
\( \LARGE \rightarrow a-b=-2 \)
حال این دو معادله در یک دستگاه حل میکنیم:
\( \LARGE \begin{cases} 4a+2b=-2 \\ a-b=-2 \end{cases} \)
معادله پایین را در یک 2 ضرب میکنیم.
\( \LARGE \begin{cases} 4a+2b=-2 \\ 2a-2b=-4 \end{cases} \)
\( \LARGE \rightarrow a = -1 , b = 1 \)
\( \LARGE y=-x^2+x+2 \)
\( \LARGE x_s = -\frac{b}{2a} =-\frac{1}{-2}=\frac{1}{2} \)
جایگذاری در معادله:
\( \Large y_s =-(\frac{1}{2})^2+\frac{1}{2}+2 \)
\( \LARGE y_s =\frac{9}{4} \)
| 1 | \( \LARGE \frac{1}{2} \) | \( \Large 0 \) | x |
|---|---|---|---|
| 2 | \( \LARGE \frac{9}{4} \) | 2 | y |
راس سهمی \( \LARGE S:( \frac{1}{2},\frac{9}{4}) \)
دهانه رو به پایین \( \LARGE a<0 \)
محور تقارن \( \LARGE x=\frac{1}{2} \)
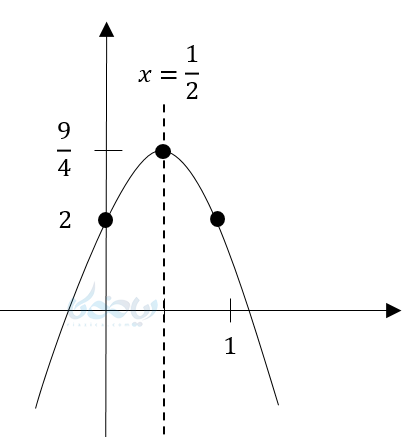
حل معادله درجه دوم از طریق آموزش رسم سهمی
با دانشی که در آموزش رسم سهمی بدست میآوریم، قادر خواهیم بود یک معادله درجه دوم را به راحتی حل کنیم. البته گاهی در این روش اگر جوابها عدد صحیح نباشند، مقدار دقیق آنها مشخص نیست. ولی به راحتی از روی رسم نمودار معادله درجه دوم میتواند تعداد جواب و علامت جوابها را متوجه شد.
- اگر معادله درجه دوم دو جواب داشته باشد، یعنی \( \Large \Delta>0 \) ، نمودار آنها محور \( \Large x \)ها را در نقاطی که همان جوابها هستند قطع میکند. یعنی داریم:
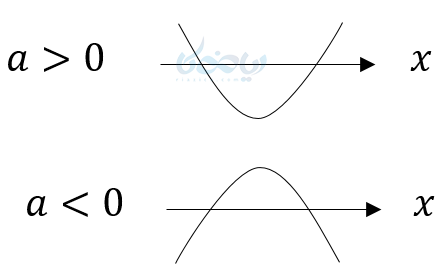
که علامت جوابها از روی قسمتی که نمودار محور \( \Large x \)ها را قطع کرده میتوان فهمید.
- اگر معادله درجه دوم یک جواب داشته باشد یعنی \( \Large \Delta=0 \)، نمودار آن در یک نقطه که همان ریشه معادله است بر محور \( \Large x \)ها مماس میشود. یعنی داریم:
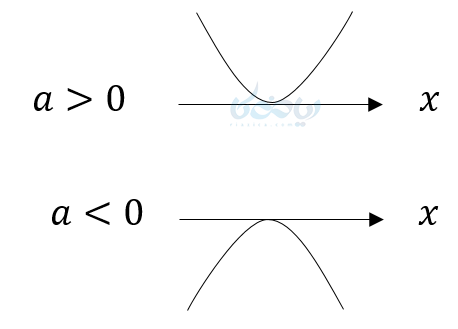
- اگر معادله درجه دوم اصلا جواب نداشته باشد، یعنی \( \Large \Delta<0 \)، آنگاه نمودار اصلا محور \( \Large x \)ها را قطع نمیکند. یعنی داریم:
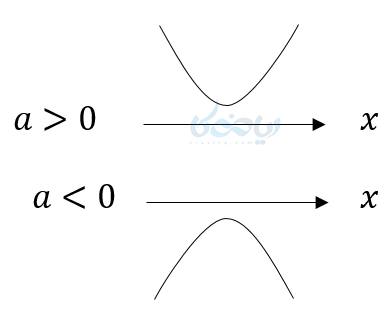
مثال ۹: با رسم نمودار معادله زیر جوابها را پیدا کنید؟
حل ۹:
\( \LARGE (x^2-2x-3=0) \)
\( \LARGE x_s = -\frac{b}{2a} =\frac{2}{2}=1 \)
جایگذاری در معادله:
\( \LARGE y_s = (1)^2-2(1)-3 \)
\( \LARGE y_s = -4 \)
| 2 | 1 | \( \Large 0 \) | x |
|---|---|---|---|
| -3 | -4 | -3 | y |
رأس سهمی \( \LARGE S:(1,-4) \)
دهانه رو به بالا \( \LARGE a>0 \)
محور تقارن \( \LARGE x=1 \)
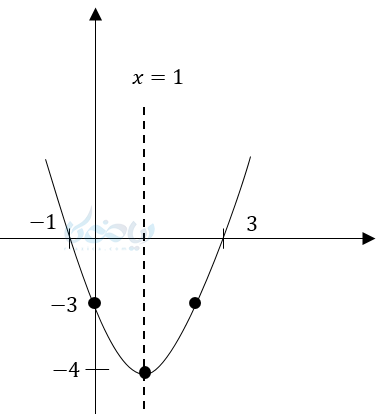
همانطور که میبینید نمودار محور\( \Large x \)ها را در دونقطه قطع کرده و یکی از جوابها منفی و دیگری مثبت است حال این معادله را از روش کلی حل میکنیم.
\( \LARGE \Delta = b^2-4ac \)
\( \LARGE \Delta= 4+12=16 \)
\( \LARGE x = \frac{-b \pm \sqrt{\Delta} }{2a} =\frac{2\pm \sqrt{4} }{2} \)
\( \LARGE x_1 = 3 , x_2 = -1 \)
نکته ۵ آموزش رسم سهمی: نقطهای که نمودار محور \( \Large y \)ها را قطع میکند، همان مقدار \( \Large c \) است. در مثال بالا \( \Large c = -3 \) است. نمودار نیز محور \( \Large y \)ها را در نقطه 3- قطع کرده است.
برای اموزش مطالب بیشتر در مورد سهمی می توانید به پست ماکزیمم و مینیمم سهمی مراجعه کنید. همینطور برای رسم سهمی به روش انتقال به پست رسم سهمی با روش انتقال مراجعه نمایید.
جمعبندی آموزش رسم سهمی با یک ویدیو کوتاه
آخر کلاس آموزش رسم سهمی
روش دیگر رسم سهمی یعنی انتقال را میتوانید در پستهای رسم توابع مشاهده کنید. برای این بخش از آموزش ریاضی دهم، نمونه سوال ریاضی دهم نیز در سایت برای علاقمندان قرار داده شده است که میتوانید از بخش محصولات سایت آنها را ببینید.
در صورتیکه که هرگونه سوالی از آموزش رسم سهمی داشتید، میتوانید سوال خود را در بخش دیدگاهها در پایین همین نوشتار مطرح کنید. گروه آموزشی ریاضیکا به سوالهایتان پاسخ میدهد.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!





عالی بود ممنون
سلام دوست عزیز ممنون از انرژی که دادید.
سلام ببخشید یه سوال در معدله سهمی aوbوc چی هستن ؟ مثلا در معادله خط می گفتیم a شیب است و… حالا در معادله سهمی چی هستن؟
سلام و عرض ادب
a یعنی ضریب x^2 نشان میدهد دهانه سهمی روبه بالا است یا پایین و همینطور باعث باز و بسته تر شدن دهانه سهمی می شود. و b روی جابجایی مکان سهمی تاثیر دارد و C محل برخورد نمودار روی محور y ها را نشان میدهد.
برای اطلاعات بیشتر به درسنامه https://riazica.com/maximum-and-minimum-quadratic-function/ مراجعه کنید.
موفق باشید.
من تو حل سوالات تستی سهمی اشکال دارم مفاهیمش رو کامل درک کردم ولی تو حل تست ها ی سختش می مونم، نمیدونم چه جوری از روابط و داده ها برای رسیدن به جواب استفاده کنم
با عرض سلام
اولا بعضی تستها استاندارد نیستن ثانیا با حل زیاد تست وتمرین به مهارت میرسید نگران نباشید
آییییی دستتون درد نکنه خیلی بکارم اومد عالی شدم تو رسمش مرسییی❤️
با سلام وعرض ادب
خوشحالیم که براتون مفید بوده معرف ما به دوستانتان باشید
.
پیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
بسیاربسیار ممنون..واقعا دستتون درد نکنه..موفق باشید…
با سلام وعرض ادب
خدا رو شکر که براتون مفید بوده
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام خسته نباشید ، ممنون از آموزش های خوبتون.
ببخشید من مثال 5 رو متوجه نمیشم چجوری تجزیه کردید، میشه توضیح بدید؟
با سلام وعرض ادب
نصف ضریب x رو نصف وبه توان دو میرسنیم وکم وزیاد کرده وضیب سه که پشت پرانتز هست رو روش تاثیر دادیم
سلام کی نمودار سهمی نوک تیز میشه
با سلام سهمی هیچ وقت نوک تیز نمیشود اون نمودار قدر مطلق هست که به صورت هفت وهشت میشه
من در x+,x_ مشمل دارم
با سلام
میشه بفرمایید پایه چندم هستید؟
سلام، خیلی مفید و عالی بود واقعا خسته نباشید??
با سلام و وقت به خیر
ممنون از انرژی مثبت شما
سلام ایکس به علاوه منفی ایکس چی میشه من خیلی تو این مشکل دارم
با سلام وادب
جمع هر عدد با قرینه اش میشه صفر
سلام. در عبارت 4x^2-4x-3=Y ابتدا سمت چپ را به ۴ تقسیم میکنیم اینگونه یک اتحاد جمله مشترک درست میشود که ریشههایش 3/2 و -1/2 هستند سپس میانگین این نقاط را به دست میاوریم که میشود 1/2 که طول محور تقارن سهمی است و عرض نقطه مینیموم میشود رأس. درست است؟ در درست بودن شک دارم.
عرض نقطه مینیموم میشود -۴ اشتباه نوشتم. ??
استاد مثال نه رو اشتباه نوشتین
سلام دوست عزیز کجاش اشتباهه؟
سلام واقعا عالی توضیح دادید متوجه شدم سپاس 🤍🙏🙏🙏🙏
با سلام
ممنون از توجه شما
سلام ببخشید سئوالی داشتم میشه لطفا پاسخ بدید و برام توضیح بدید ، ما یه معادله ای داریم که هست ایگرگ مساوی با پرانتز باز ایکس منهای دو، پرانتز بسته به توان دو این نمودار سهمیش چه جوری به دست میاد آیا من می تونم به جای ایکس دوتا ۰ بدم و یه دونه دونم بدم؟
با سلام وادب
دوست عزیز در درسنامه بالا کامل توضیح داده شده
این سوال شما راس سهمی نقطه (۲،۰) است و دهانه سهمی رو به بالا است بهترین روش در راس سهمی اینه که راس رو پیدا کنید ویه نقطه قبل وبعد رو هم پیدا کنید وسهمی رو رسم کنید
توی روش دوم پیدا کردن راس از رابطه … توی اثباتش آخرین x^2 باید x باشه نه x^2
با سلام اصلاح شد ممنون از دقت شما