آموزش ریاضی پایه دهم
آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
آموزش ریشه گیری در ریاضی دهم مبحثی مهم در ریاضیات، هندسه، فیزیک و شیمی و هر جایی که با حساب کردن سر و کار داریم است. بنابراین یادگیری و تبحر در ساده کردن رادیکالها و کار با آن بسیار مهم است. با توجه به اینکه در تستها نیز جوابها به سادهترین شکل ممکن نوشته میشود، لزوم یادگیری بهتر آن بیشتر میگردد.
ریشه دوم در آموزش ریشه گیری در ریاضی دهم
به عبارت زیر دقت کنید:
\( \LARGE \begin{cases} (-2)^2=4 \\ (2)^2=4 \end{cases} \)
بنابر تعریف 2 و 2- ریشههای دوم عدد 4 هستند. اما بنابه قرارداد وقتی مینویسیم \( \Large \sqrt 4 \)، آن ریشهای که مثبت است را در نظر میگیریم و میدانیم ریشه دوم یا جذر عدد 4، ۲ میشود( \( \Large \sqrt 4 = 2 \) ).
دقت کنید اعداد منفی ریشه دوم ندارند. چون هیچ عددی وجود ندارد که در خودش ضرب شده و منفی شود. به مثالهای زیر دقت کنید:
| 81 | 16 | 4 | عدد |
|---|---|---|---|
| ۹ , – ۹ | ۴ , – ۴ | ۲ , – ۲ | ریشههای دوم |
پس به طور کلی هر عدد مثبت دو ریشه دوم دارد که قرینه یکدیگر هستند.
به مثالهای زیر دقت کنید:
(1
\( \LARGE \sqrt 16 = 4 \)
\( \LARGE \rightarrow \sqrt {2^4} = 4 \)
(2
\( \LARGE \sqrt {(-2)^2} = \sqrt 4 = 2 \)
\( \LARGE \rightarrow \sqrt {(-2)^2} = \left| -2 \right| \)
پس داریم:
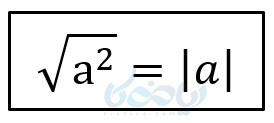
نکته ۱ در آموزش ریشه گیری در ریاضی دهم: رادیکالهای زیر را بیمعنی هستند زیرا مقادیر زیر رادیکال منفی هستند.
(1
\( \LARGE \sqrt {-25} \)
(2
\( \LARGE \sqrt {(-2)^3} \)
(3
\( \LARGE \sqrt {3 \times (-2)} \)
مقدار تقریبی ریشه دوم اعدادی که مجذور کامل نیستند.
میدانیم ریشه دوم همه اعداد مثبت یک عدد صحیح نمیشود. مثلاً \( \Large \sqrt 20 \). اما میتوانیم مقدار تقریبی ریشه دوم این عدد را پیدا کنیم.
عدد 20 بین دو عدد مجذور کامل 16 و 25 قرار دارد. پس ریشه دوم یا همان جذرش بین جذر این دو عدد یعنی 4 و 5 قراردارد. یعنی:
\( \LARGE \sqrt {16} < \sqrt {20} < \sqrt {25} \)
\( \LARGE 4 < \sqrt {20} < 5 \)
حال اگر بخواهیم مقدار تقریبی آن را تا یک رقم اعشار پیدا کنیم، کافیست حدس بزنیم. چون 20 فاصلهاش تا 16 و 25 تقریباً یک اندازه است، پس حدس میزنیم جذر آن تقریباً \( \Large 4.5 \) شود. حال حدس خود را امتحان میکنیم.
\( \LARGE (4.5)^2=20.25 \)
چون مقدار این عدد از 20 بیشتر شد، پس حدس خود را به \( \Large 4.4 \) تغییر میدهیم.
\( \LARGE (4.4)^2=19.36 \)
\( \LARGE \rightarrow \sqrt 20 = 4.4 \)
به همین ترتیب میتوانیم جذر تقریبی را تا چند رقم اعشار بدون استفاده از ماشین حساب، و یا با استفاده از راهحلهایی که در پایههای قبل خواندیم حدس بزنیم.
ریشه سوم در آموزش ریشه گیری در ریاضی دهم
میدانیم رابطهٔ زیر برقرار است:
\( \Large 3^3=27 , (-3)^3=-27 \)
پس میتوانیم بنویسیم:
\( \LARGE \sqrt [3] {27} =3 , \sqrt [3] {-27} =-3 \)
و میخوانیم ریشه سوم عدد 27 میشود 3، و ریشه سوم 27- میشود 3-. نتیجه:
پس هر عدد (چه مثبت و چه منفی) یک ریشه سوم دارد.
نکتهٔ ۲ در آموزش ریشه گیری در ریاضی دهم: به ریشه سوم، کعب نیز گفته میشود. یعنی \( \LARGE \sqrt [3] {27} =3 \) خوانده میشود ،کعب 27 میشود 3.
\( \LARGE 2^3 = 8 \Leftrightarrow \sqrt [3] {8}=2 \)
\( \LARGE (-2)^3 = -8 \Leftrightarrow \sqrt [3] {-8}= -2 \)
و به طور کلی میتوان گفت هر عدد یک ریشه سوم دارد:
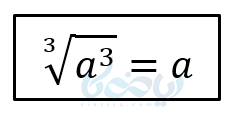
مقدار تقریبی اعدادی که ریشه سوم کامل ندارند
ریشه سوم همه اعداد، عدد صحیح نمیشود. مانند: \( \LARGE \sqrt [3] {90} \). اما میتوان مقدار تقریبی ریشهٔ سوم این اعداد را پیدا کنیم. میدانیم 90 بین دو عدد مکعب کامل 64 و 125 قراردارد. پس ریشه سوم آن نیز بین دو عدد 4 و 5 خواهد بود. یعنی:
\( \LARGE \sqrt [3] {64} < \sqrt [3] {90} < \sqrt [3] {125} \)
\( \LARGE 4 < \sqrt [3] {90} < 5 \)
حال اگر بخواهیم تا یک رقم اعشار آن را محاسبه کنیم، میبینیم فاصله 90 تا 64 کمتر است. پس حدس میزنیم ریشهٔ سوم آن تقریباً \( \Large 4/2 \) خواهد بود.
\( \LARGE \sqrt [3] {90} \simeq 4.2 \)
\( \LARGE \rightarrow (4.2)^3=74.088 \)
چون این عدد فاصلهاش با 90 زیاد است، به حدس خود اضافه میکنیم.
\( \LARGE \sqrt [3] {90} \simeq 4.4 \)
\( \LARGE \rightarrow (4.4)^3=85.184 \)
اگر باز به حدس خود اضافه کنیم، خواهیم داشت:
\( \LARGE \sqrt [3] {90} \simeq 4.5 \)
\( \LARGE \rightarrow (4.5)^3=91.125 \)
چون این عدد از 90 بیشتر است، پس قابل قبول نیست. پس نتیجه میگیریم ریشه سوم 90 تا یک رقم اعشار \( \Large 4.4 \) خواهد بود.
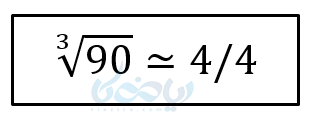
ریشه چهارم و ریشههای زوج در آموزش ریشه گیری دهم
میدانیم رابطه زیر برقرار است:
\( \LARGE \begin{cases} (-2)^4=16 \\ (2)^4=16 \end{cases} \)
پس 2 و 2- ریشههای چهارم عدد 16 هستند. اما بنابه قرارداد وقتی مینویسیم \( \LARGE \sqrt [4] {16} \) و میخوانیم ریشه چهارم عدد 16، آن ریشهای که مثبت است را در نظر میگیریم. یعنی \( \LARGE \sqrt [4] {16} =2 \). پس هر عدد مثبت دو ریشه چهارم دارد که قرینهٔ یکدیگرند. به همین ترتیب میتوان ریشه ششم، هشتم و غیره را تعریف کرد و نتیجه بگیریم:
هر عدد مثبت دارای دو ریشه زوج است که قرینه یکدیگرند.
ریشهی پنجم و ریشههای فرد
میدانیم
\( \LARGE \begin{cases} (3)^5=243 \\ (-3)^5=-243 \end{cases} \)
\( \LARGE \rightarrow \begin{cases} \sqrt [5] {243} = 3 \\ \sqrt [5] {-243} = -3 \end{cases} \)
پس هر عدد چه منفی چه مثبت دارای یک ریشه پنجم است. که اگر عدد مثبت باشد ریشه پنجم آن مثبت و اگر منفی باشد ریشه پنجم آن منفی است. این مطلب برای تمام توانهای فرد برقرار است.
پس به طور کلی داریم:
هر عدد (چه مثبت و چه منفی) فقط دارای یک ریشه فرد میباشد.
تعریف ریشه n اُم
اگر \( \Large n \geq 2 \) یک عدد طبیعی باشد، \( \Large b \) را یک ریشه \( \Large n \) اُم عدد \( \Large a \) مینامیم. هرگاه \( \Large b^n = a \) یا به زبان ریاضی داریم:
\( \LARGE b^n = a \Leftrightarrow \sqrt [n] {a} = b \)
نکته ۳ در آموزش ریشه گیری دهم: دقت داشته باشید در این تعریف وقتی n یک عدد زوج است، a باید مثبت باشد. چون اعداد منفی ریشهٔ زوج ندارند.
همین طور داریم:

نکته ۴: هرگاه مینویسیم \( \Large \sqrt [n] {a} \) ، اگر \( \Large n \) زوج باشد، ما \( \Large a \) را مثبت یا صفر در نظر میگیریم.
قوانین رادیکالها در آموزش ریشه گیری دهم
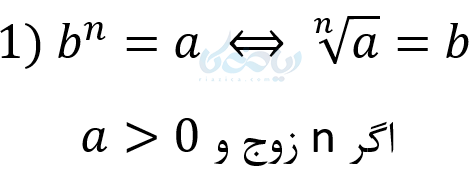
کاربرد ریشهگیری
شاید این سوال برایتان پیش بیاید که دانستن این مطالب چه کاربردی دارد؟ در خیلی از معادلات در درسهای مختلف ما به دنبال ریشههای مختلف اعداد هستیم. به مثال زیر دقت کنید:
\( \LARGE x^2=9 \)
\( \LARGE \rightarrow x= \pm \sqrt 9 = \pm 3 \)
معنای این معادله این است که چه اعدادی به توان دو برسند 9 خواهند شد. میدانیم هم 3 و هم 3- به توان دو برسند 9 میشوند. یعنی 3 و 3- ریشههای دوم 9 هستند.
چند مثال دیگر برای فهم بهتر از آموزش ریشه گیری دهم
(1
\( \LARGE x^2=5 \)
ریشه دوم میگیریم
\( \LARGE \rightarrow x= \pm \sqrt 5 \)
(2
\( \LARGE x^4=16 \)
ریشه چهارم میگیریم
\( \LARGE \rightarrow x = \pm \sqrt {16} = \pm 2 \)
(3
\( \LARGE x^3=27 \)
ریشه سوم میگیریم
\( \LARGE \rightarrow x=3 \)
(4
\( \LARGE x^3=-64 \)
ریشه سوم میگیریم
\( \LARGE \rightarrow x = -4 \)
(5
\( \LARGE x^6=64 \)
ریشه ششم میگیریم
\( \LARGE \rightarrow x= \pm \sqrt {64} = \pm 4 \)
(6
\( \LARGE x^5=-243 \)
ریشه پنجم میگیریم
\( \LARGE \rightarrow x=-3 \)
مسئله 1: مساحت مربعی 81 مترمربع است. طول ضلع مربع چقدر است؟
یک ضلع به توان 2 = S
\( \LARGE \rightarrow x^2=81 \)
\( \LARGE \rightarrow x=\pm 9 \)
امّا میدانیم که ضلع مربع منفی نمیتواند باشد. پس فقط جواب \( \Large x=9 \) قابل قبول است.
مسئله 2: حجم منبع آبی به شکل مکعب 300 لیتر است. ارتفاع این مکعب را تا یک رقم اعشار حساب کنید.
\( \LARGE V=x^3 \)
\( \LARGE \rightarrow x^3=300 \)
\( \LARGE \rightarrow x=\sqrt [3] {300} \simeq 6/6\)
\( \LARGE \sqrt [3] {216} < \sqrt [3] {300} < \sqrt [3] {343} \)
\( \LARGE 6< \sqrt [3] {300} < 7 \)
چون 300 به 343 نزدیکتر است، پس حدس میزنیم اعشار آن \( \Large 6.7 \) باشد. اما \( \Large (6.7)^3=300.763 \) پس چون از 300 بیشتر است یک رقم کم میکنیم.
\( \Large (6/6)^3=487/496 \)
مسئله ۳: جمله پنجم یک دنباله هندسی 64 و جمله دهم آن 2048 است. قدرنسبت این دنباله چقدر است؟
\( \LARGE \begin{cases} a^5=a_1 r^4 \\ a_{10}=a_1 r^9 \end{cases} \)
\( \LARGE \rightarrow \begin{cases} 61=a_1 r^4 \\ 2048 = a_1 r^9 \end{cases} \)
\( \LARGE \rightarrow \frac{a_{10}}{a^5}=\frac{a_1 r^9}{a_1 r^4 }=\frac{2048}{64} \)
\( \LARGE \rightarrow r^5=32 \)
\( \LARGE \rightarrow r=\sqrt [5] {32} = \sqrt [5] {2^5} = 2 \)
چند نکته در مورد ساده کردن رادیکالها
- برای ساده کردن رادیکالها، اگر زیر رادیکال عدد داشتیم ابتدا آن را تجزیه میکنیم. اگر توان عدد حاصل از فرجه کمتر باشد عدد از زیر رادیکال ساده نمیشود.
\( \LARGE \sqrt [6] {32} = \sqrt [6] {2^5} \)
ساده نمیشود.
\( \LARGE \sqrt [5] {a^2 b^3} \)
ساده نمیشود.
- اگر توان عدد تجزیه شده یا متغیر زیر رادیکال بر فرجه بخشپذیر باشد، عدد یا متغیر ساده شده و از زیر رادیکال بیرون میآید و توانش به فرجه تقسیم میگردد.
(1
\( \LARGE \sqrt [5] {32} = \sqrt [5] {2^5} =2 \)
(2
\( \LARGE \sqrt [6] {64 a^{12} b^3} \)
\( \LARGE = \sqrt [6] {2^6 a^{12} b^3} \)
\( \LARGE = 2a^2 \sqrt [6] {b^3} \)
- اگر توان عدد تجزیه شده یا متغیر زیر رادیکال از فرجه بزرگتر ولی بر ان بخشپذیر نباشد، توان را میشکنیم و سپس ساده میکنیم:
(1
\( \LARGE \sqrt [4] {32} \)
\( \LARGE = \sqrt [4] {2^5} = \sqrt [4] {2^4 \times 2} \)
\( \LARGE = 2 \sqrt [4] {2} = 2 \sqrt [4] {2} \)
(2
\( \LARGE \sqrt [5] {a^5 b^{19} } = \)
\( \LARGE \sqrt [5] {a^5 \times b^{15} \times b^4 } \)
\( \LARGE = ab^3 \sqrt [5] {b^4 } \)
مثال در آموزش ریشه گیری در ریاضی دهم: عبارتهای زیر را ساده کنید.
(1
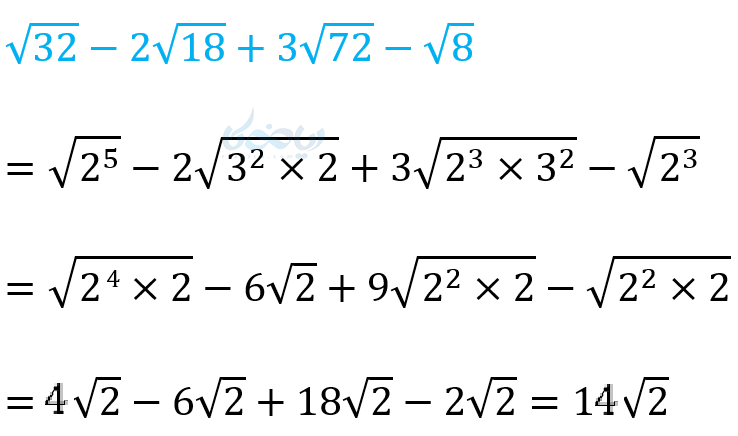
(2
(3
(4
مقایسه ریشهها و اعداد تواندار در آموزش ریشه گیری در ریاضی دهم
- اعداد بزرگتر از یک هرچه به توان برسند بزرگتر و هرچه در ریشهگیری پیشروی کنیم کوچکتر میشوند.
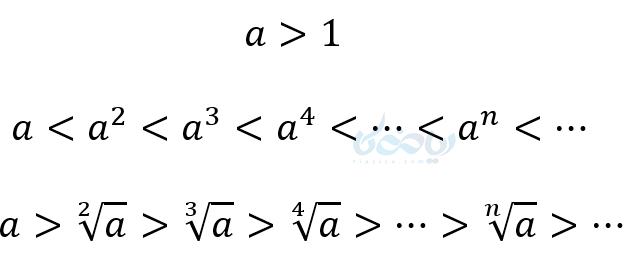
مثال در آموزش ریشه گیری در ریاضی دهم:
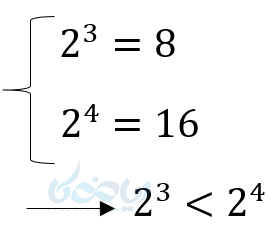
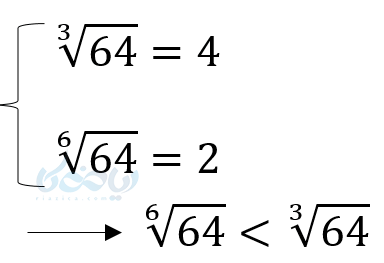
- اعداد بین صفر و یک هرچه به توان برسند کوچکتر شده و هرچه در ریشهگیری پیشرفت کنیم بزرگتر میشوند.
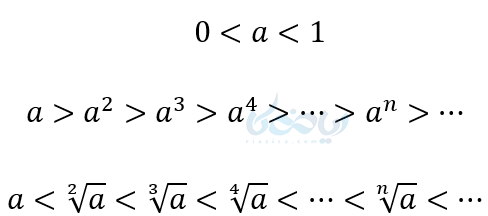
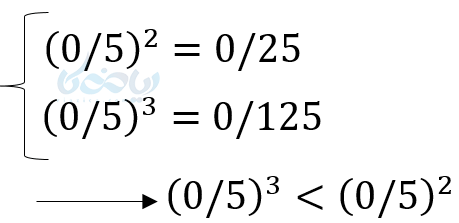
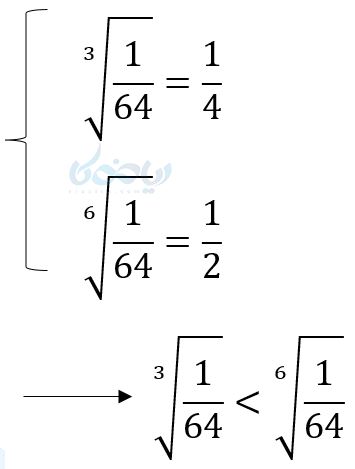
- اعداد بین \( \Large -1<a<0 \) میدانیم اگر به توان زوج برسند مثبت میشوند و بزرگتر میشوند. امّا اگر به توان فرد برسند هرچه توان بیشتر باشد آنها بزرگتر میشوند و وقتی ریشه فرد آنها گرفته میشود هرچه بزرگتر شود مقدار آنها کوچکتر میشود.
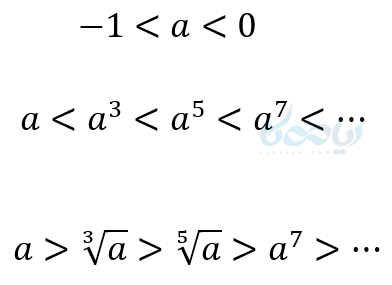
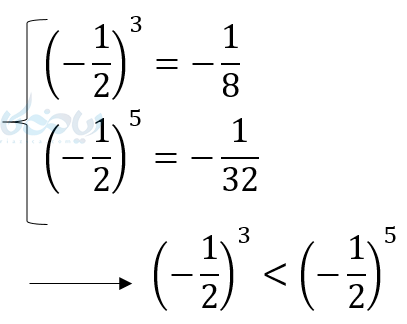
در اعداد منفی هر چه عدد از نظر عددی (بدون در نظر گرفتن علامت منفی) بزرگتر باشد از نظر مقدار کمتر است. - در اعداد کوچکتر از 1- نیز اگر به توان زوج برسند که بزرگتر میشوند. ولی وقتی به توان فرد میرسند هرچه توان بزرگتر شود مقدارشان کمتر میشود و وقتی ریشه فرد میگیریم هرچه فرجه بزرگتر، مقدارشان بیشتر میشود.
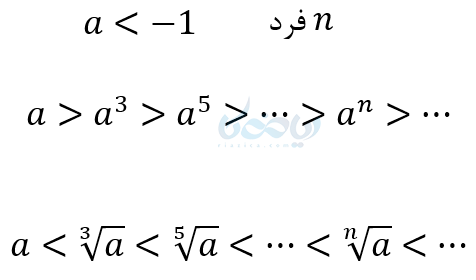
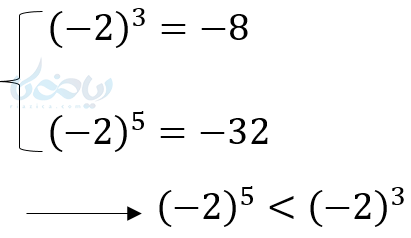
نکته در آموزش ریشه گیری در ریاضی دهم: برای به خاطر سپردن اعداد بزرگتر از یک و اعداد بین \( \Large -1<a<0 \) مثل هم با این فرق که اعداد منفی فقط ریشه فرد دارند و اعداد بین صفر و یک و اعداد کوچکتر از 1- مانند هم هستند.
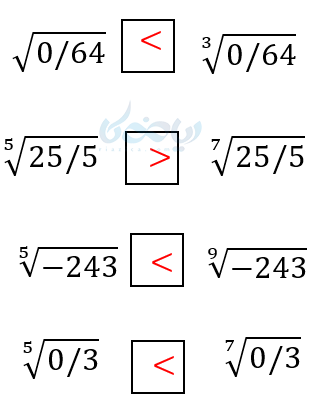
مثال: در جاهای خالی علامت مناسب بگذارید. (< و = و >)
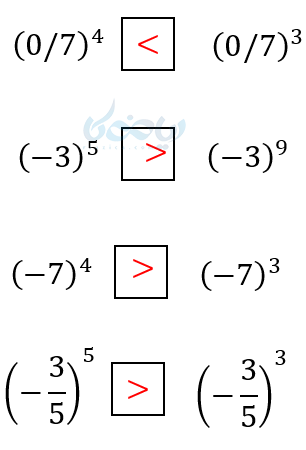
زنگ آخر درس آموزش ریشه گیری دهم
بچهها با هم در ریاضیکا آموزش ریشه گیری دهم که از مباحث مهم و کاربردی است را یادگرفتیم. در این آموزش دهها مثال مختلف را برای فهم بهتر باهم بررسی کردیم.
ادامهٔ آموزش ریاضی دهم را میتوانید در همین سایت مطالعه کنید. هرچه سوال از این نوشتار داشتید را در قسمت دیدگاهها در پایین همین بخش مطرح کنید. بچههای ریاضیکا حتما به سوالات شما پاسخ میدهند. موفق باشید 🙂
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!



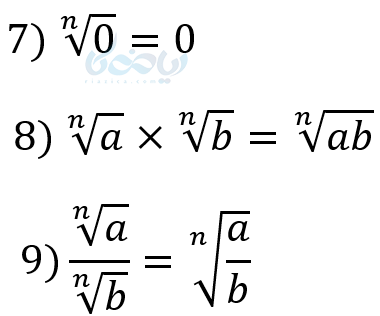
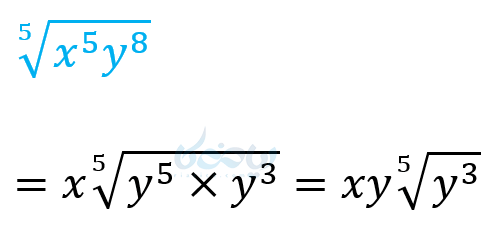
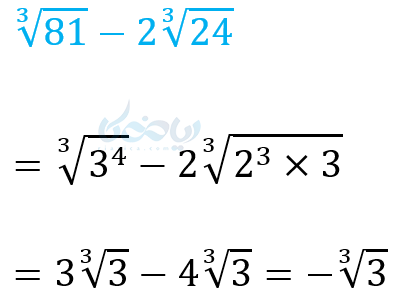

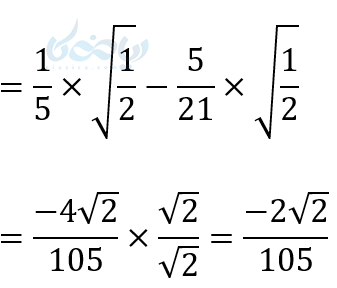


عالی بود خیلی ممنونم
ضمن عرض سلام
خیلی خوشحالیم که براتون مفید بوده مطالب
موفق و پیروز باشید
???
????
عالییییی
بهترین جزوه ای بود که درمورد ریشه گیری خوندم
مطالبتون خیلی مفید بود
ممنون از زحمات شما
سلام و عرض ادب
ممنون از پیام پرمهرتون.
موفق باشید.
بد ترین جزوه دنیا است
سلام و عرض ادب
ممنون از توجهتون. سپاسگذار میشم مشکلی که داشتید برایمان بیان کنید.
موفق باشید.
خیلی خیلی مفید بود
با عرض ادب وتشکر
خوشحالیم که براتون مفید بوده
متشکرم بخاطر مطالب مفیدتون
با سلام واحترام
خواهش میکنم دوست عزیز
سلام میشه گفت ایکس رادیکال ۹ همیشه میشه ۹ ؟ حالا ایکس هر عددی باشه ؟؟
با سلام
خیر مقدار ایکس تغییر کنه اونم تغییر میکنه
سلام. ببخشید من یه سوال دارم. آیا رادیکال ایکس دو , و رادیکال ایکس، به توان با هم تفاوتی در جواب دارند؟ نظر بنده این هست که از اولی قدرمطلق ایکس و از دومی خود ایکس خارج میشه درسته؟
با سلام
درست میگید فقط توی دومی از اول باید شرط ایکس بزرگتر از صفر در نظر گرفته بشه وگرنه بی معنی هست
عالی بود.
درود خسته نباشید.
با اختلاف بهترین سایتی هستین که حتی من به ویدیو های آموزشی ترجیهش میدم و خیلی کاملن مطالبتون ولی توی این مطلب یه مشکل هست.
در قسمت سوم از (مقایسه ریشهها و اعداد تواندار) مقایسه ها برعکس هستن.فرمودین اعداد بین صفر و منفی یک هرچقدر توان فردشون بیشتر باشه همونقدر بزرگترن درحالی که برعکس اینه.
همچنین فرمودین رادیکال فرجه فرد اونها نیز هرچقدر بیشتر باشه اونقدر بزرگترن که این هم برعکسه.
در هر حال تا الان من مفید ترین مطالب ریاضیمو از ریاضیکا آموختم و دست بوس شما هستم.
با سلام و ادب
ممنون از لطف شما وانرژی شما ممنون از توجه شما بررسی و تصحیح میشود
شرمنده شب بود حواسم نبود غلط حل کردم مطالب کاملا صحیح هستن دستتون درد نکنه.
محمد رضاسبقت اللهی با سلام آقای سید ایمان موسوی نطنزی
در وب سایت ریشه گیری در ریاصی دهم:زیر رادیکال نمون
riazica.com
در قسمت چند نکته در مورو ساده کردن رادیکال ها
(گزینه ۳ اگر توان عدد تجزیه شده یا متغیر زیر رادیکال از فرجه بزرگتر ولی بر آن بخش پدیر نباشد توان را می شکنیم وسمس ساده می کنیم)
در ساده کردن رادیکال ۳۲ با فرجه ۴
جواب صحیح ۲رادیکال۲ بافرجه ۴ می باشد
دصورتیکه شما ۴رادیکال۲ بافرجه ۴ ثبت کرده اید
اگه جواب من صحیحه لطفاً اصلاح نمایید
با تشکر وارادت محمد رضا سبقت اللهی
۱۴/۳/۱/۱۴
با سلام
ممنون از دقت شما دوست عزیز
تصحیح شد