آموزش ریاضی پایه دهم

آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!

آخرین بروزرسانی در تاریخ 1402/09/19 توسط سید ایمان موسوی نطنزی
آموزش الگو به راحتی آب خوردن!
15
فروردین

اولین چیزی که در آموزش الگو و دنباله خواهیم فهمید، این است که دنیای اطراف ما سرشار از الگوهای متنوع و گوناگونی است. مانند طرح‌های روی یک گل آفتابگردان، شکل‌های هندسی روی کاشی‌کاری‌ها، مارپیچ‌های روی میوه‌های آناناس و هزاران مثال دیگر.

یکی از وظایف و رسالت‌های مهم ریاضی مدل‌سازی کردن پدیده‌های طبیعی است. به طوریکه برخی ریاضیدانان، ریاضی را علم مطالعه الگوها نامیده‌اند. بنابراین آموزش الگو و دنباله در ریاضیات مبحث مهمی است که در این نوشتار به آن می‌پردازیم.

آموزش الگو و دنباله : یک تعریف اولیه

الگو یک ساختار منظم از موارد زیر است:

  • اشکال
  • تصاویر
  • صداها
  • نمادها
  • وقایع
  • اعداد

این موارد مختلف ممکن است تکرارشونده یا رشد‌کننده یا ترکیبی از این دو باشند. الگو خطی، شکل زیر را در نظر بگیرید:

الگو یک ساختار منظم از اشکال ، تصاویر ، صداها ، نمادها و وقایع یا اعداد است.

اگر تعداد دایره‌ها‌ی شکل را دنبال هم بنویسیم خواهیم داشت:
11 ، 8 ، 5
حدس میزنید عدد بعدی چند باشد؟
اگر پاسخ شما ۱۴ باشد، درست حدس زده‌اید. همانطور که می‌بینید به هر شکل 3 دایره اضافه می‌شود. پس این دنباله اعداد اینطور ادامه می‌یابد:

\( \LARGE a_6 \) \( \LARGE a_5 \) \( \LARGE a_4 \) \( \LARGE a_3 \) \( \LARGE a_2 \) \( \LARGE a_1 \)
20 17 14 11 8 5

وقتی یک سری عدد را دنبال هم می‌نویسیم، یک دنباله از اعداد تشکیل می‌شوند. به هر کدام از این اعداد یک جمله می‌گویند. جمله اول را با \( \Large a_1 \) ، جمله دوم \( \Large a_2 \) و جمله \( \Large n \) اُم دنباله را جمله عمومی دنباله می‌نامند. در آموزش الگو و دنباله جمله عمومی را با \( \LARGE a_n \) نمایش می‌دهند.

خرید پکیج دوره محاسبات سریع 💎🔮

397.000 تومانافزودن به سبد خرید

الگوی خطی در آموزش الگو و دنباله

در برخی از دنباله‌ها مانند مثال بالا، اختلاف دو جمله متوالی مقداری ثابت است. این دنباله دارای یک الگوی خاص است و می‌توان جمله عمومی آن را به صورت یک عبارت درجه اول نوشت. به چنین عبارتی الگو خطی گفته می‌شود.
در مثال بالا الگو یا همان جمله عمومی دنباله به صورت \( \Large a_n = 3n + 2 \) است. به نظر شما چگونه می توان این الگو را پیدا کرد؟ یک روش حدس و گمان و با دسته‌بندی شکل و پیدا کردن یک الگو مشترک است.

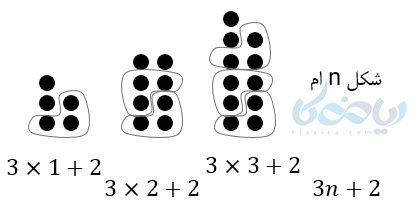
روش حدس و گمان و با دسته بندی شکل و پیدا کردن یک الگو مشترک می باشد .

اما چرا به این الگو ، الگو خطی می‌گویند؟ به دو علت:

  1. الگوی آن یک عبارت درجه یک است.
  2. اگر اعداد دنباله را روی محور مختصات نشان دهیم همه نقاط در امتداد یک خط راست قرار دارند. در مثال بالا داریم :

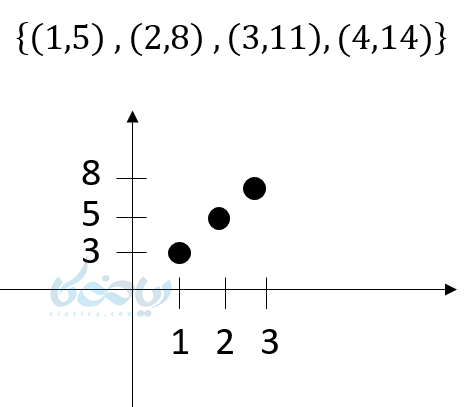
با الگو خطی می توانیم اعداد دنباله را روی محور مختصات نشان دهیم .

ما در سال گذشته آموختیم که با داشتن دو نقطه از یک خط می‌توانیم معادله آن خط را بنویسیم در الگو خطی نیز می توانیم داشتن دو جمله از یک الگو خطی جمله عمومی آن را بنویسیم.

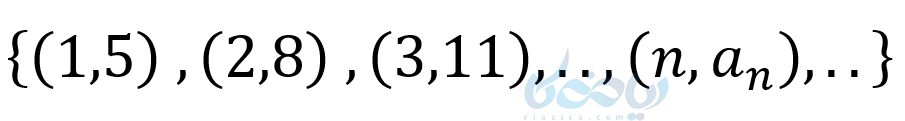
با داشتن دو نقطه از یک خط می توانیم معادله آن خط را بنویسیم.

شیب

\( \LARGE m = \frac{8-5}{2-1} = 3 \)

\( \LARGE y = ax + b \)

\( \LARGE 5 = 3 \times 1 + b \)

\( \LARGE b = 2 \)

\( \LARGE y = 3x + 2 \)

\( \LARGE a_n = 3n + 2 \)

می‌دانستیم معادله هر خط به صورت زیر است:

\( \LARGE y = ax + b \)

که در این الگو \( \Large x \) همان \( \Large n \) و \( \Large y \) همان \( \Large a_n \) است. پس می‌توان گفت جمله عمومی تمام الگوهای خطی به صورت زیر خواهد بود:

\( \LARGE a_n = a\times n + b \)

که در آن \( \Large a \) همان شیب خط است. در واقع تفاضل دو جمله متوالی الگوی خطی است و با قرار دادن یکی از جملات به جای \( \Large n \) و \( \Large a_n  \) می‌توان \( \Large b \) را به دست آورد. مثلاً اگر جمله اول الگو 5 باشد، خواهیم داشت:

\( \LARGE a_n = a_1 = 5 \)

\( \LARGE n = 1 \)

که اگر این دو مقدار را جایگذاری کنیم \( \Large b \) به دست می‌آید. البته لزوماً نباید جمله اول را جایگذاری کرد. بلکه هر جمله دیگری نیز می‌توان جایگزین شود. مثلاً اگر جمله سوم را می‌خواهیم استفاده کنیم باید به صورت زیر عمل کنیم:

\( \LARGE a_n = a_3 = 11 \)

\( \LARGE n = 3 \)

مثال 1 آموزش الگو و دنباله: الگوی زیر چه الگویی است؟ جمله عمومی این الگو را بنویسید و سپس جمله دهم این دنباله را بنویسید.

\( \LARGE 2 , 6 , 10 , 14 \)

حل 1: این الگو خطی است. چون فاصله تمام جملات 4 واحد است. پس مقدار \( \Large a = 4 \) خواهد بود.

\( \LARGE a_n = a_1 = 2 \)

\( \LARGE n = 1 \)

\( \LARGE a = 4 \)

\( \LARGE a_n = a \times n + b \)

\( \LARGE 2 = 4 \times 1 + b \)

\( \LARGE  b = -2 \)

پس جمله عمومی این الگو

\( \LARGE a_n = 4 \times n – 2 \)

خواهد بود

جمله دهم

\( \LARGE a_{10} = 4 \times 10 – 2 = 38 \)

نکته ۱: جمله عمومی به صورت:

\( \LARGE c_n , b_n , t_n , a_n \)

و غیره نیز می‌نویسند.

مثال 2 آموزش الگو و دنباله: جمله سوم یک الگوی خطی 13 و جمله دهم آن 41 است. جمله این الگو را بنویسید.
حل 2:
راه اول
\( \Large a \) همان شیب خط است و جمله سوم \( \Large a_3 = 13 \). پس یک نقطه به صورت \( \Large (3 , 13) \) داریم. \( \Large a_{10} = 41 \) یعنی نقطه دیگر \( \Large (10 , 41) \). پس شیب خط به صورت زیر است:

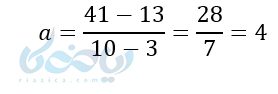محاسبه شیب خطحال یکی از جملات را در الگوی جمله عمومی به همراه مقدار \( \Large a \) جایگذاری کرده و \( \Large b \) را پیدا می‌کنیم.

\( \LARGE t_n = a \times n + b \)

\( \LARGE 41 = 4 \times 10 + b \)

\( \LARGE b = 1 \)

\( \LARGE t_n = 4 \times n + 1 \)

راه دوم :

\( \LARGE \begin{cases} a_3 = 13 \\ a_{10} = 41 \end{cases} \rightarrow \)

\( \LARGE \begin{cases} 3a + b =13 \\ 10a + b = 41 \end{cases}  \)

حل دستگاه:

\( \LARGE b = 1 , a = 4  \)

\( \LARGE t_n = 4n +1  \)

خرید پکیج دوره محاسبات سریع 💎🔮

397.000 تومانافزودن به سبد خرید

آموزش الگو و دنباله : الگوهای غیر خطی

اگر یک سری عدد دنبال هم نوشته شوند، به آن‌ها دنباله می‌گوییم که یکی از این دنباله‌ها همان دنباله خطی بود. اما آیا تمام دنباله‌ها دارای الگو هستند‌؟ آن هم از نوع خطی؟
جواب منفی است. دنباله‌ها می‌توانند دارای الگو باشند یا هیچ الگویی نداشته باشند‌. می‌توانند متناهی یا نامتناهی باشند. می‌توانند الگو داشته باشند. ولی الگوی آنها از نوع خطی نباشد. به مثال زیر دقت کنید:

مثال ۳ آموزش الگو و دنباله: اگر نمرات درس ریاضی ترم اول کلاس را دنبال هم به ترتیب لیست اسامی دانش آموزان بنویسیم، یک دنباله تشکیل می‌شود که نه تنها الگو ندارد، متناهی نیز هست.

\( \LARGE 17 , 18 , 5 , 10 , 20 , 18 , 14 \)

ولی در ریاضیات بحث ما بیشتر روی دنباله‌هایی است که دارای الگو هستند. می‌توان برای جمله عمومی آن، الگو نوشت و توسط آن بقیه جملات را می‌توان پیدا کرد. به دنبال زیر توجه کنید:

\( \LARGE 1 , 4 , 9 , 16 , 25 , .. , a_n , .. \)

آیا دنباله بالا یک الگو دارد؟ آیا الگو آن خطی است؟ جواب این است که این دنباله الگو دارد ولی الگوی آن از نوع خطی نیست و جمله عمومی آن به صورت زیر است:

\( \LARGE a_n = n^2 \)

شکل هندسی این دنباله نیز به صورت زیر خواهد بود:

شکل هندسی الگو غیر خطی n*n

همانطور که ملاحظه می‌کنید جملات این دنباله مجذور اعداد طبیعی هستند و شکل آن هم به صورت مربع است. برای همین این الگو را مربعی نامیده‌اند و از طرفی چون جمله عمومی آن درجه دوم است، طبق آموزش الگو و دنباله به آن الگو غیر خطی درجه دوم می‌گویند.

مثال دیگری از الگو غیر خطی الگوی مثلثی است که به صورت زیر است:

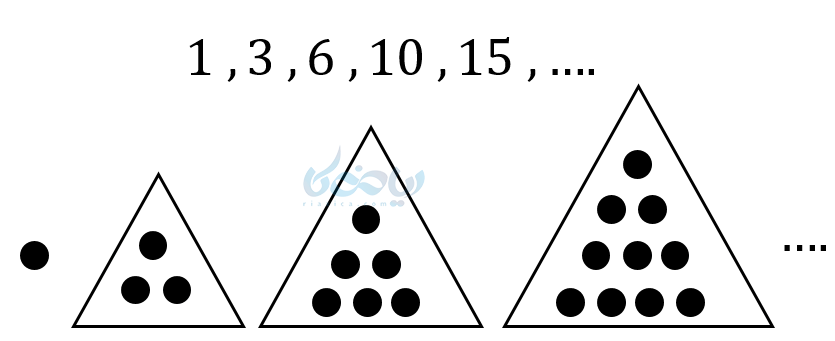
الگو غیر خطی الگوی مثلثی

جمله الگوی غیرخطی مثلث به صورت زیر خواهد بود:

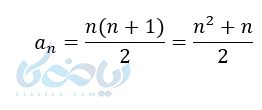
جمله الگوی غیر خطی مثلث

باید به این نکته دقت کرد که الگوی غیر خطی مثلثی نیز از نوع درجه دوم است. البته لازم به ذکر است که الگو های غیر خطی همگی از نوع درجه دوم نیستند. بلکه می‌توانند درجات بالاتر نیز داشته باشند یا به صورت کسری و غیره نیز باشند .

مثال ۴ آموزش الگو و دنباله: در زیر جمله عمومی چند دنباله نوشته شده است. در هر یک چهار جمله اول دنباله را بنویسید.

حل ۴:

(1

\( \LARGE a_n = 2n + 1 \)

\( \LARGE 3 , 5 , 7 , 9 , … \)

(2

\( \LARGE a_n = \frac{n+3}{n} \)

\( \LARGE 4 , \frac{5}{2} , 2 , \frac{7}{4} \)

(3

\( \LARGE a_n = n^2 + 2n – 1 \)

\( \LARGE 2 , 7 , 14 , 23 , … \)

(4

\( \LARGE a_n = 2n^3 + 3 \)

\( \LARGE 5 , 19 , 57 , 131 , … \)

چگونه برای دنباله‌هایی با الگوهای غیرخطی الگو بنویسیم؟

گاهی جملات یا شکل هندسی یک الگو غیر خطی را داریم و می خواهیم برای آن «الگو»، یا همان «جمله عمومی» را بنویسیم. لازم به ذکر است که نوشتن الگو همیشه کار ساده ای نیست. باید با تعمق و تفکر و پیدا کردن رابطه‌ای بین جملات دنباله به الگوی آن‌ها پی ببریم‌.

طریقه نوشتن الگوی غیر خطی درجه دوم با استفاده از الگوی مربعی ومثلثی

اما آنچه در دستور کار کتاب ریاضی دهم آمده الگوهای غیرخطی درجه دوم است. که باید سعی کنیم رابطه ای بین دنباله داده شده و دنباله مربعی یا مثلثی و گاهی هر دو را پیدا کنیم. به مثال زیر دقت کنید:

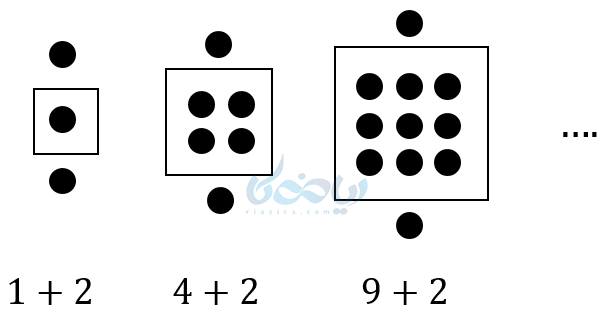
جملات یا شکل هندسی یک الگو غیر خطی را داریم و می خواهیم برای آن الگو یا همان جمله عمومی را بنویسیم

همانطور که مشاهده می کنید جملات دنباله مربعی به علاوه عدد 2 شده‌اند‌. پس جمله عمومی دنباله به صورت زیر است:

\( \LARGE a_n = n^2 + 2 \)

مثال 4: الگو دنباله زیر را پیدا کنید؟

\( \LARGE 2 , 4 , 7 , 11 , 16 , … \)

حل 4: همانطور که دقت می‌کنید در می‌یابید که دنباله، یک دنباله غیر خطی است. چون جملات با یک مقدار ثابت تغییر نکرده‌اند. اگر جملات دنبالهٔ مثلثی را بشناسید، می‌بینید رابطه زیر با دنباله مثلثی برقرار است.

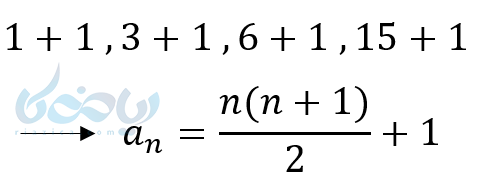
دنباله یک دنباله غیر خطی می باشد چون جملات با یک مقدار ثابت تغییر نکرده اند

مثال 5 آموزش الگو و دنباله: جمله عمومی دنباله زیر را بنویسید.

\( \LARGE 5 , 12 , 21 , 32 , … \)

حل 5:

برای پیدا کردن الگو دنباله بالا یک راه رسم شکل به صورت دسته بندی منظم و پیدا کردن رابطه‌ای بین دنباله مربعی یا مثلثی با دنباله بالا است. اگر بخواهیم برای دنباله بالا شکل رسم کنیم، می توانیم از الگوی زیر استفاده کنیم:

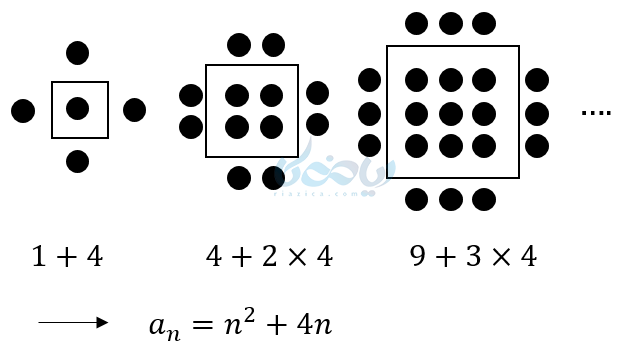
پیدا کردن الگو دنباله بالا یک راه رسم شکل به صورت دسته بندی منظم و پیدا کردن رابطه ای بین دنباله مربعی یا مثلثی

البته خود رسم شکل و پیدا کردن این رابطه احتیاج به دقت و تمرین دارد. حال می‌خواهیم ببینیم اصلاً تشخیص اینکه آیا این دنباله از نوع درجه دوم است یا نه، چگونه خواهد بود؟ و آیا راهی برای نوشتن جمله عمومی بدون رسم شکل وجود دارد؟

طریقه نوشتن الگوی غیر خطی درجه دوم با استفاده از فرمول معادله درجه دوم

دوباره به مثال پایین دقت کنید. همانطور که می‌بینید فاصلهٔ پایین جملات دنباله ثابت نیست.

فاصله پایین جملات دنباله ثابت نیست .

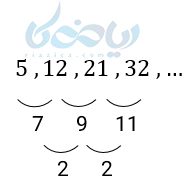
اما فاصلهٔ فاصله جملات یک مقدار ثابت بوده که در این مثال 2 است. پس این الگو از نوع غیر خطی درجه دوم است. از طرف جمله عمومی تمام الگوهای غیر خطی درجه دوم به صورت زیر است:

\( \LARGE a_n =an^2 + bn +c \)

حال ما باید \( \Large a \) , \( \Large b \) , \( \Large c \) را پیدا کنیم تا جمله عمومی را داشته باشیم. در این مثال دیدید فاصلهٔ فاصله جملات 2 است. این مقدار همیشه 2 برابر a خواهد بود. پس:

\( \LARGE 2a = 2 \)

\( \LARGE a = 1 \)

حال باید مقدار \( \Large b \) , \( \Large c \) را پیدا کنیم. مانند الگوی خطی کافیست دوتا از جملات دنباله را در الگوی دنباله جایگذاری کنیم. در این مثال داریم:

\( \LARGE a_n = an^2 + bn + c \)

\( \LARGE a_1 = 5 \rightarrow n = 1 \)

\( \LARGE 5 = 1 \times 1^2 + b \times 1 + c \)

\( \LARGE b + c = 4 \)

\( \LARGE a_2 = 12 \rightarrow n = 2 \)

\( \LARGE 12 = 1 \times2^2 + b \times 2 \)

\( \LARGE 2b + c =8 \)

\( \LARGE \begin{cases} b + c = 4 \\ 2b + c =8 \end{cases}  \)

حل دستگاه:

\( \LARGE b = 4 , c = 0 \)

\( \LARGE a_n = n^2 + 4n  \)

با این روش می‌توان تمام الگوی غیر خطی درجه دوم را پیدا کرد.

مثال 6 آموزش الگو و دنباله: دنباله زیر چه نوع دنباله‌ای است؟ الگوی آن را بنویسید.

الگو

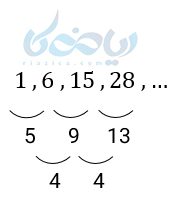
حل 6:

همانطور که می‌بینید دنباله یک دنبالهٔ غیر خطی درجه دوم است. حال می‌خواهیم جمله عمومی را پیدا کنیم.

\( \LARGE a_n = an^2 + bn + c \)

\( \LARGE 2a = 4 \rightarrow a = 2 \)

\( \LARGE a_1 = 1 \rightarrow n = 1 \)

\( \LARGE 1 = 2 \times 1^2 + b \times 1 + c  \)

\( \LARGE b + c = -1 \)

\( \LARGE a_2 = 6 \rightarrow n = 2  \)

\( \LARGE 6 = 2 \times 2^2 + b \times 2 + c  \)

\( \LARGE 2b + c = -2 \)

\( \LARGE \begin{cases} b + c = -1 \\ 2b + c = -2 \end{cases}  \)

حل دستگاه:

\( \LARGE b = -1 , c = 0 \)

\( \LARGE a_n = 2n^2 – n  \)

در ادامه حتما  درسنامه آموزش دنباله حسابی را مطالعه کنید.

ویدیو آموزش الگو و دنباله

در این ویدیو با یک مثال طریقه نوشتن جمله عمومی الگو های غیر خطی درجه دوم ازآموزش الگو ودنباله گفته شده است.

زنگ آخر کلاس آموزش الگو و دنباله

در این آموزش از مجموعهٔ آموزش ریاضی دهم ریاضیکا، باهم در مورد مبحث مهم آموزش الگو و دنباله صحبت کردیم. این مبحث را با مثال‌های متنوعی بررسی کردیم. همچنین برای فهم بیشتر از اشکال مختلفی که دنباله‌های گوناگون را برایمان بهتر توصیف می‌کردند استفاده کردیم.

در صورتیکه هر سوالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سوالات شما پاسخ خواهند داد.

خرید پکیج دوره محاسبات سریع 💎🔮

397.000 تومانافزودن به سبد خرید

به خوندن ادامه بده!متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️اصل شمارش ، بدون شمردن ✖️🚫آموزش حل نامعادله همراه با رسم نمودار و مثال‌های متنوع↪️📝تابع ثابت را در حافظه خود ثابت کنید 📊📐آموزش حل معادله درجه دو + 4 روش‌ مختلف حل آن4️⃣📝تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗تابع چند جمله‌ ای به زبان ساده ✖️🔤تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚آموزش دنباله حسابی 🧮🔢 – از همیشه ساده‌تر؟آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈آموزش جایگشت یا جابجایی 🔁❗️ مفهومی‌ترین آموزشآموزش احتمال دهم – کامل‌ترین و جامع‌ترین آموزش 🔣❓آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!‌محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزهگویا کردن مخرج‌ گنگ 🚰🤐 مثل آب خوردن!آموزش نسبت‌های مثلثاتی: توضیحات کامل 📶✅همراه با تصویرتجزیه عبارت‌ های جبری به 4 روش مختلف 4️⃣❗️عبارت های گویا ➗🚰به سادگی آب خوردنآموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️

ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی دهم به شما پیشنهاد می‌دهیم:
سید ایمان موسوی نطنزی

52 دیدگاه برای “آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶! ”

  1. عاطفه گفته:

    برای الگوی غیرخطی ۵.۱۲.۲۲.۳۵.۵۱ از راه حل اخری نمیشه رفت اختلاف فاصله ها سه میشه ولی جمله عمومی ما وقتی n را ۲ میگذاریم جواب یچیز دیگر میاد?

    پاسخ
      • بهناز گفته:

        سلام دوست عزیز شما هم که اشتباه جواب دادید a میشه ۳/۲و bمیشه ۵/۲و cهم میشه ۱

        پاسخ
    • 20farzad04 گفته:

      داش صفحه ۲۰ ریاضی دهم تجربی مگه نیس تمرین ۴
      خیلی راحته با روش آخری فقط کافیه a رو یک و نیم بگیریم b میشه دو و نیم c هم میشه ۱

      پاسخ
        • ناشناس گفته:

          سلام وقت بخیر،
          واقعا خیلی خیلی ممنون بابت آموزشاتون من خیلی تو فهمیدنشون مشکل داشتم❤

          پاسخ
          • دبیر ارشد ریاضیکا گفته:

            با سلام خدا رو شکر که مفید واقع شده

        • دبیر ارشد ریاضیکا گفته:

          با سلام وادب
          ممنون از پکیج خط به خط ریاضی دهم هم میتونید استفاده کنید مطالب مختصر ومفید گفته شده

          پاسخ
  2. احمدی گفته:

    در الگوی خطی جملات دوم وپنجم قرینه هم وجمله هفتم برابر هفت است. جمله عمومی را بیابید

    پاسخ
  3. احمدی گفته:

    در الگوی خطی جملات دوم وپنجم قرینه هم هستند وجمله هفتم برابر 7 میباشد.. الگوی عمومی رابیابید

    پاسخ
    • سید ایمان موسوی نطنزی گفته:

      سلام متن کامل مطالعه کنید به جوابتان می رسید و این برایتان لدت بخش تر است.

      پاسخ
    • سید ایمان موسوی نطنزی گفته:

      سلام و عرض ادب
      ممنون از انرژی و پیام پرمهرتون.
      موفق باشید

      پاسخ
  7. سارا گفته:

    سلام
    الگوی بین اعداد 14و 45و 106 رو چطور میتونم پیدا کنم؟
    ممنون میشم راهنمایی بفرمایید.

    پاسخ
    • سید ایمان موسوی نطنزی گفته:

      با سلام وعرض ادب
      با سه تا جمله نمیشه حدس زد ولی گمان میکنم هر بار سی تا به مقدار قبلی اضافه میشه اگه این طور باشه مربعی هست وما راه حلش رو درپست گفتیم

      پاسخ
      • ناشناس گفته:

        به جمله دوم سی و یکی و جمله سوم 61 ای اضافه شده یکم پیچیده تر از الگوهای بالاست.

        پاسخ
  8. سید ایمان موسوی نطنزی گفته:

    با سلام
    با توجه به این سه تا جمله نمیشه گفت چند تا دیگه جمله لازم هست

    پاسخ
  9. سارا گفته:

    به جمله دوم 31 ای و جمله سوم 61 ای به ماقبلش اضافه شده است و به نظر پیچیده تر از الگوهای بالا رفتار می کند.
    در واقع مجموعه اعداد به این شکل است:
    (0,1), (1,14), (2,45),(3,106),…

    پاسخ
    • سید ایمان موسوی نطنزی گفته:

      اگه جمله چهارم ۱۹۷ باشه دنباله مربعی هست و در پست گفتیم چه جوری دنباله اون رو بدست بیارید

      پاسخ
  11. ناشناس گفته:

    خیلی خوب بودن مطالبی که نوشتید من کلی استفاده کردم
    ولی یه مثالی بالای مثال 6 هست که اشتباه داره توی جایگزاری جمله دوم اشتباهی nرو یک گرفتید ولی باید 2 باشه جواب رو در کل درسته ولی اون اشتباه تایپیدشده

    پاسخ
    • دبیر ارشد ریاضیکا گفته:

      با سلام وعرض ادب
      خوشحالیم که برای شما مفید واقع شده بله اشتباه تایپی بود اصلاح شد ممنون از دقت نظر شما
      برای یاد گیری بهتر میتونید ازپکیج خط به خط ریاضی دهم هم اسنفاده کنید

      پاسخ
  13. موسوی گفته:

    سلام
    جمله ۲۰ام این دنباله چه عددی میشه
    ۳/۳۷ ، ۵/۵۱، ۱/۸ ، ۳/۱۷، ۱/۳

    پاسخ
    • دبیر ارشد ریاضیکا گفته:

      با سلام وادب
      ممنون که سایت ما ومطالب ما رو دنبال میکنید

      پاسخ
  18. ریحانه گفته:

    اگه اختلاف اختلاف ها ثابت نباشه باید چی کار کنیم؟چجوری جمله عمومی را پیدا کنیم؟

    پاسخ
    • دبیر ارشد ریاضیکا گفته:

      با سلام وادب
      در این صورت دیگه غیر خطی درجه دوم نیست وپیدا کردن الگو اونها به این راحتی نیست و کتاب دهم هم از شما نمیخواد

      پاسخ
  19. دانیال گفته:

    سلام آیا الگوی غیر خطی درجه دو حالا بجز الگو های معروف مانند مثلثی و مربعی و…، همه هندسی هستند؟ سپاس

    پاسخ
    • دبیر ارشد ریاضیکا گفته:

      با سلام وادب
      منظورتون از هندسی چیست؟یعنی نمایش هندسی دارن؟

      پاسخ
  20. فرزاد گفته:

    سلام
    اگر دنباله با یک عدد غیر ثابت تغییر کنه، باید چیکار کرد؟
    مثلا ۱٫۳٫۱۱٫۴۷٫۲۳۹٫…

    پاسخ
    • دبیر ارشد ریاضیکا گفته:

      با سلام
      در دنباله غیر خطی همیشه پیدا کردن الگو کار راحتی نیست

      پاسخ
  22. دبیر ارشد ریاضیکا گفته:

    <با سلام دنباله حسابی وخطی یکی هستن ولی غیر خطی شامل دنباله هایزیادی هست کههندسی یکی از اونها میشه

    پاسخ
  23. ناشناس گفته:

    سلام
    در مثال ۴ در بخش چهارم، چهارمین الگو اشتباه نوشته شده
    جواب ۱۳۱ میشه

    پاسخ
    • سید ایمان موسوی نطنزی گفته:

      با سلام وادب
      ممنون از دقت نظر شما اصلاح شد.

      پاسخ
  24. ..... گفته:

    میشه بگید a+b+c و 2a و 3a+b خودشون چطور تشکیل شدن ینی میشه اینارو اثبات کنید؟

    پاسخ
    • سید ایمان موسوی نطنزی گفته:

      با
      سلام وادب
      دوست عزیز کامل در پست بالا توضیح دادیم

      پاسخ

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *