آموزش ریاضی پایه دهم
دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
دی
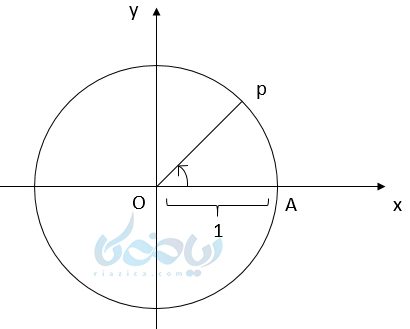
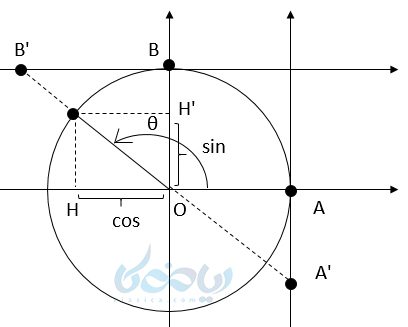
برای شروع آموزش دایره مثلثاتی یا دایره واحد، ابتدا باید یک دایره بکشیم. مرکز این دایره مبدأ مختصات و شعاع آن یک واحد است. نقطه A که محل برخورد دایره با جهت مثبت محور طول‌ها می‌باشد را به عنوان مبدأ حرکت در نظر می‌گیریم. متحرکی روی دایره از نقطه A شروع به حرکت بر خلاف جهت عقربه‌های ساعت می‌کند و زاویه AOP را به وجود می‌آورد. زاویه بدست آمده یک زاویهٔ مثبت است.
حال اگر همان متحرک از A هم جهت با عقربه‌های ساعت حرکت کند زاویه به دست آمده منفی خواهد بود. به چنین دایره‌ای، دایره مثلثاتی می گویند. همچنین به زوایای به دست آمده زاویه استاندارد گفته میشود.
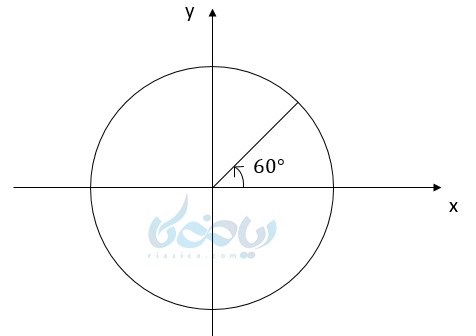
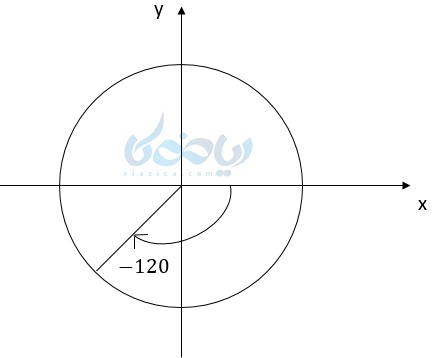
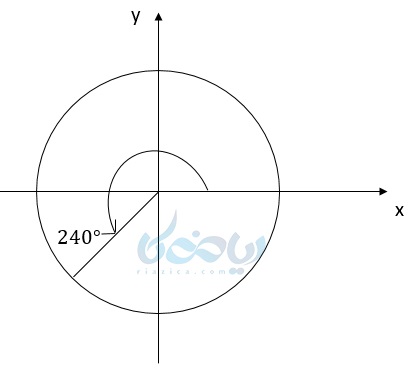
مثال ۱: زاویه‌های 60 ، 120- ، 240 درجه را روی دایره مثلثاتی نشان دهید.
انتهای زاویه 60 درجه در ربع اول قرار دارد.
انتهای زاویه 120- درجه در ربع سوم قرار دارد.
انتهای زاویه 240 درجه در ربع سوم قرار دارد.
رابطه بین نسبتهای مثلثاتی و دایره مثلثاتی
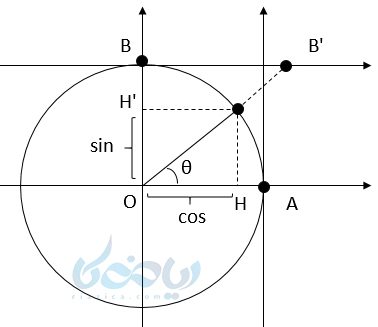
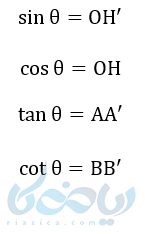
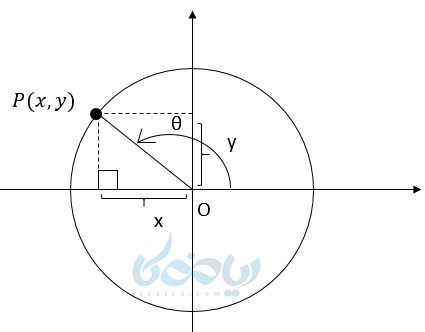
نقطهٔ (p(x,y نقطه‌ای دلخواه روی دایره مثلثاتی در شکل زیر است. از نقطه A به اندازه \( \Large \theta \) درجه در خلاف عقربه‌های ساعت دوران می‌کنیم تا به نقطه p برسیم. حال اگر از p به محور xها عمود کنیم، مثلث قائم الزاویهٔ OPQ را خواهیم داشت که:
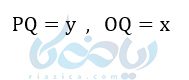
اگر نسبتهای مثلثاتی \( \Large \theta \) را بنویسیم (p(x,y خواهیم داشت:
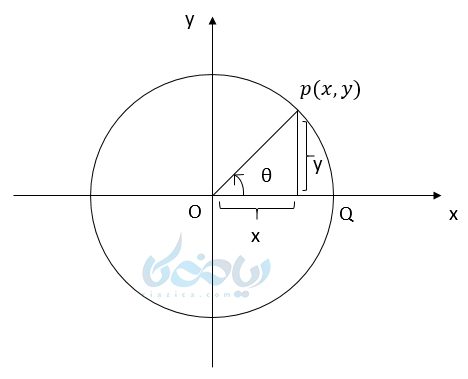
پس نتیجه می‌گیریم وقتی روی دایره مثلثاتی به اندازه \( \Large \theta \) دوران می‌کنیم و به نقطهٔ p می‌رسیم به دو نتیجه زیر می‌رسیم:
- طول این نقطه برابر کسینوس مقدار دوران خواهد بود.
- عرض این نقطه برابر سینوس مقدار دوران خواهد بود.
مثال ۲: اگر به اندازه 60 درجه دوران کنیم مختصات نقطه \( \Large p = ( \frac{1}{2} , \frac{\sqrt{3}}{2}) \) است
انتهای زاویه 60 درجه در ربع اول قرار دارد.
زاویه‌های مرزی و اندازه نسبتهای مثلثاتی آنها
می‌دانیم محورهای مختصات دایره مثلثاتی را به چهار ربع تقسیم می کنند که نامگذاری ربع‌ها نیز بر خلاف عقربه‌های ساعت است. طبق جدول زیر زاویه‌های مختلف در ربع‌های مختلف به این ترتیب قرار دارند.
| ربع | زاویه + | زاویه – |
|---|---|---|
| ربع اول | 0 < θ < 90 | -360 < θ < -270 |
| ربع دوم | 90 < θ < 180 | -270 < θ < -180 |
| ربع سوم | 180 < θ < 270 | -180 < θ < -90 |
| ربع چهارم | 270< θ < 360 | -90 < θ < 0 |
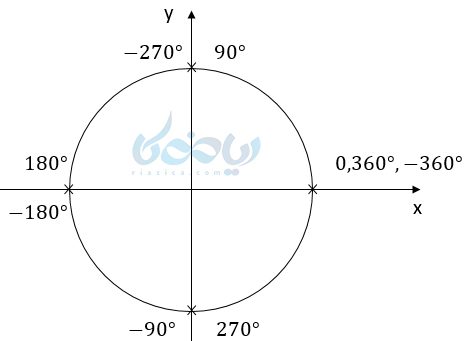
اما زاویه‌های مرزی درست در مرز بین دو ربع قرار دارند. برای مثال صفر درجه درست در مبدأ یا همان مرز ربع اول و چهارم قرار دارد. در ادامه موقعیت سایر زاویه‌های مرزی را می‌توانید ببینید:
- 90 و 270- درجه مرز بین ربع اول و دوم.
- 180 و 180- درجه مرز بین ربع دوم و سوم.
- 360 و 90- درجه مرز بین ربع سوم و چهارم.
- 360- و 360 درجه مرز بین ربع چهار و دوم.
می‌دانیم علامت طول و عرض در ربع‌های مختلف تغییر می‌کند. پس علامت نسبتهای مثلثاتی نیز در ربع‌های مختلف با هم فرق دارند. مثلاً 120 درجه در ربع دوم است. می‌دانیم علامت x در این ربع منفی و علامت y مثبت است. پس sin در این ربع مثبت و cos در این ربع منفی می‌باشد. یعنی:
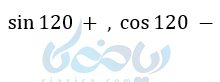
به طور کلی داریم :
| نسبت مثلثاتی | ربع اول | ربع دوم | ربع سوم | ربع چهارم |
|---|---|---|---|---|
| sin θ | + | + | – | – |
| cos θ | + | – | – | + |
| tan θ | + | – | + | – |
| cot θ | + | – | + | – |
می‌توانید از کلیدواژهٔ هستک برای به خاطر سپردن علامت ربع‌ها استفاده کنید. این کلیدواژه علامتِ مثبت در هر ربع را نشان می‌دهد.
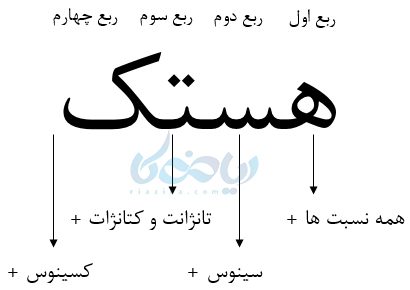
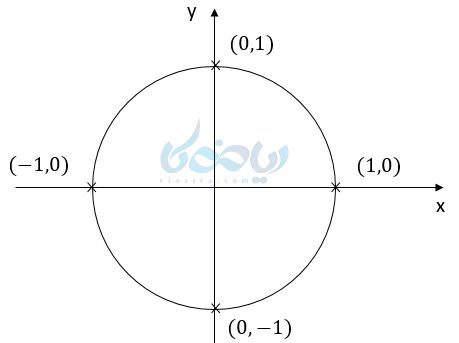
با توجه به اینکه شعاع دایره مثلثاتی 1 واحد است، پس مختصات نقاط مرزی به صورت زیر خواهند بود:
با توجه به شکل بالا داریم:
به همین ترتیب برای بقیه زاویه‌های مرزی می‌توانیم بنویسیم:
| نسبت مثلثاتی | \( \Large 0 \) | 90 درجه
270- درجه |
180 درجه
180- درجه |
270 درجه
90- درجه |
360 درجه
360- درجه |
|---|---|---|---|---|---|
| sin θ | \( \Large 0 \) | 1 | \( \Large 0 \) | -1 | \( \Large 0 \) |
| cos θ | 1 | \( \Large 0 \) | -1 | \( \Large 0 \) | 1 |
| tan θ | \( \Large 0 \) | ت | \( \Large 0 \) | ت | \( \Large 0 \) |
| cot θ | ت | \( \Large 0 \) | ت | \( \Large 0 \) | ت |
ت = تعریف نشده
نکته ۱: با توجه به دایره مثلثاتی در می‌یابیم که بیشترین مقدار برای سینوس و کسینوس هر زاویه دلخواه ۱ و کمترین مقدار ۱- است.
اما مقدار \( \Large tan\theta \) و \( \Large cot \theta \) می تواند در محدوده‌ٔ \( \Large (-\infty , +\infty) \) متغیر باشد.
آموزش دایره مثلثاتی: محورها
همانطور که در دایره مثلثاتی دیدید، طول هر نقطه روی دایره با cos مقدار دوران برابر بود. برای همین به محور طول‌ها در دایره مثلثاتی محور کسینوس‌ها گفته میشود. و محور عرض‌ها هر نقطه روی دایره مثلثاتی با سینوس مقدار دوران برابر بود. پس به محور عرض‌ها نیز محور سینوس‌ها گفته میشود. اما محور تانژانت‌ها و کتانژانت‌ها چگونه هستند؟
اگر از نقطه A یعنی مبدا دایره مثلثاتی خطی موازی محور سینوس‌ها بکشیم، به این محور، محور تانژانت‌ها گفته میشود. همچنین اگر از نقطه B محوری موازی با محور کسینوس‌ها رسم شود، به این محور، محور کتانژانت‌ها گفته میشود.
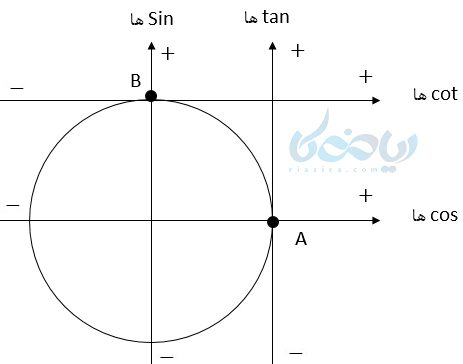
حال زاویه \( \Large \theta \) را در ربع اول در نظر بگیرید. اگر از این زاویه به محور سینوس‌ها و کسینوس‌ها عمود کنیم، مقدار این دو نسبت و علامت آنها مشخص میشود. اگر انتهای این زاویه را ادامه دهیم تا محور \( \Large tan\theta \) و \( \Large cot \theta \) را قطع کند، می‌توانیم اندازه و علامت این نسبت‌ها را نیز مشاهده کنیم.
همانطور که می‌بینید علامت همگی مثبت است.
نکته ۲: نکتهٔ دیگری که در این ربع باید دقت کنید این است که هرچه \( \Large \theta \) در این ربع بزرگتر میشود مقدار cos کمتر و مقدار sin بیشتر میشود. همینطور هر چه مقدار زاویه بیشتر میشود مقدار تانژانت بیشتر از کتانژانت میشود.
حال اگر \( \Large \theta \) در ربع دوم باشد داریم:
که علامت \( \Large \sin \) مثبت و بقیه منفی هستند. پس در ربع دوم مقدار کسینوس همواره منفی و کمتر از سینوس است. در مورد تانژانت و کتانژانت هر دو منفی هستند. پس هر چه زاویه بزرگتر میشود مقدار تانژانت نیز بیشتر میشود. ( از نظر عددی کوچکتر اما از نظر مقدار بیشتر میشود. )
به همین ترتیب می‌توانید با استقاده از دایره مثلثاتی مقدار نسبتهای مثلثاتی را در دو ربع یگر بررسی کنید.
بدست آوردن نسبتهای مثلثاتی با داشتن یک سینوس یا کسینوس
مثال ۳: فرض کنید \( \Large sin{\theta} = \frac{3}{4} \) و \( \Large \theta \) در ربع دوم واقع شده باشد. سایر نسبتهای مثلثاتی \( \theta \) را بدست آورید.
می‌دانیم:
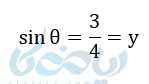
از طرفی طبق شکل و رابطه فیثاغورس داریم:
پس :
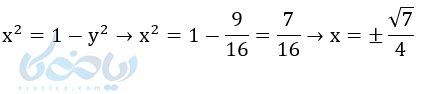
ولی چون \( \Large \theta \) در ربع دوم است و در ربع دوم طول نقطه p منفی است پس:
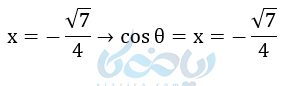
حال برای به دست آوردن \( \Large tan{\theta} = \frac{y}{x} \) می‌توانیم به این شکل عمل کنیم: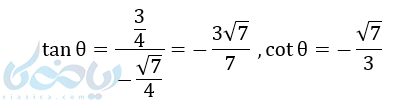
آموزش دایره مثلثاتی: رابطه بین شیب خط با تانژانت زاویه
همانطور که قبلاً آموخته‌ایم شیب هر خط برابر است با نسبت تفاضل عرض‌ها به طول‌ها. یعنی:
حال به شکل زیر دقت کنید و دو نقطه A , B را روی خط مورب در نظر بگیرید:
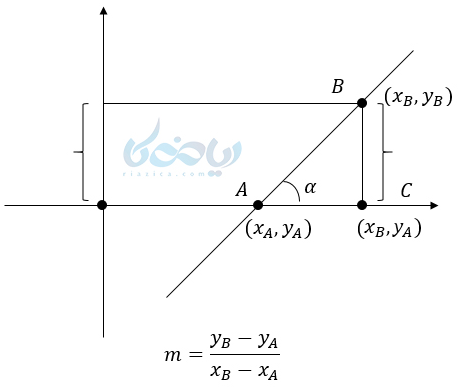
حال به نقطهٔ C دقت کنید که طولش با طول نقطهٔ B و عرض آن عرض نقطهٔ A برابر است. پس داریم :
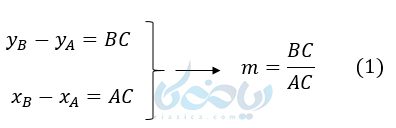از طرفی :
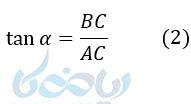
مهم: پس از رابطهٔ 1 و 2 نتیجه می‌گیریم که شیب هر خط با تانژانت زاویه‌ای که خط با جهت مثبت محور xها می‌سازد برابر است. (منظور این است هر خطی که محور \( \Large x \)ها را قطع می‌کند، با آن دو زاویه می‌سازد. یکی سمت راست و دیگری سمت چپ. شیب با تانژانت زاویه‌ای که سمت راست است برابر خواهد بود)
مثال ۴: خطی به معادله \( \Large 3x – \sqrt{3}y = 2 \) با جهت مثبت محور \( \Large x \)ها چه زاویه‌ای می‌سازد ؟
جواب :
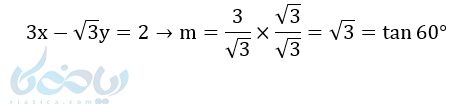
پس خط با جهت مثبت محور xها زاویهٔ 60 درجه می‌سازد.
مثال ۵: معادله خطی که در شکل زیر مشاهده می‌کنید را بنویسید.
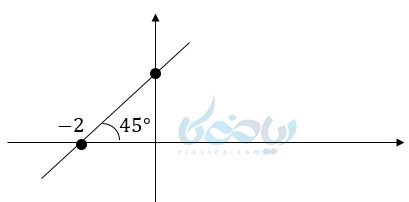
جواب :
برای آموزش مطالب بیشتر در مورد مثلثات به پستهای محاسبه مساحت بدون داشتن ارتفاع و آموزش نسبت های مثلثاتی و روابط بین نسبتهای مثلثاتی مراجع کنید
ویدیو از دایره مثلثاتی یا دایره واحد
در این ویدیو تمرین ۲ صفحه ۴۵ کتاب ریاضی دهم حل شده است.
آخر کلاس آموزش دایره مثلثاتی یا دایره واحد
در این آموزش سعی کردیم همه چیز را به صورت کامل همراه با تصاویر برای شما دانش‌آموزان عزیز آموزش دهیم. اگر از این مبحث هر سوالی دارید می‌توانید با مطرح کردن آن در بخش دیدگاه‌ها در پایین همین صفحه آن را با ما در میان بگذارید. ما در ریاضیکا به پرسش‌های شما پاسخ می‌دهیم.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی دهم به شما پیشنهاد می‌دهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!
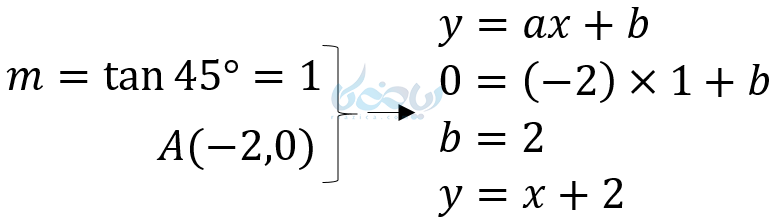
با عرض سلام و خسته نباشید.
آیا در دایره‌ای با شعاع غیرواحد نیز می‌توان نسبتهای مثلثاتی را تعریف کرد؟
سلام بر شما دوست عزیز
در واقع فرقی نمی‌کند، چون نسبت‌ها تقسیم بر شعاع می‌شوند و در نهایت با هم ساده خواهند شد. پس برای راحتی کار ما دایره واحد را در نظر می‌گیریم.
خیلی ممنون لطف کردید
واقعا عالی.
دمتون گرم ????
ممنون از لطف شما دوست عزیز
سلام
فایل پی دی اف این محتوا رو دارید؟
سلام
بله تا چند وقت دیگ فایل پی دی اف تمامی مطالب روی سایت قرار می‌گیرد.
ممنون از توجهتان
من نفهميدم
با سلام واحترام
میشه بگید دقیقا کجا رو نفهمیدید ما مطالب رو به ساده ترین شکل ممکن مینویسیم
عالی
خیلی خوب بودش.
فقط مثل نکات سهمی برا این ویدیو دارید؟
ضمن عرض سلام
نکاتی در رابطه با این ویدیو ساختیم که در کانال آپارات و اینستاگراممون وجود داره. بزودی هم در این پست براتون ویدیوهای مربوطه اش قرار داده میشه
سلام واقعا عالی بود
ضمن عرض سلام
خوشحالیم که برای شما مفید و آموزنده بوده است.
سلام استاد من مشغول برنامه نویسی هستم و سوالاتی دارم یعنی به فرمول هایی احتیاج دارم، لطفا اگه تلگرام دارید به پی وی بنده بیایید یا آیدی تلگرامتان را در ایمیل بنده بفرستید من مزاحم شوم ممنونم.راستش من مشغول فهم و کاربرد این فرمول ها هستم و در برنامه نویسی توابعی نوشتم که مختصات کامپیوتر رو به مختصات کارتیزن(cartesian) یا همون دکارتی تبدیل میکنه و بلعکس یعنی من همه چیز رو آماده کردم تا این فرمول هارو یاد بگیرم با این تفاوت که اولا من فرمول هارو به برنامه میدم و جوابشو اون حساب میکنه ثانیه هدفم در واقع استفاده از این فرمول ها در کنترل ربات هاست.مثلا ربات اسکارا (scara) یا ربات دلتا (delta) و به طور کلی ربات های بازویی که طبق تحقیقاتم همشون از زیر مبنای فرمولی و محاسباتی دارند استفاده میکنند از جمله همین فرمول های مثلثاتی
بنظرم درسته که ما از یک فرمول میتونیم فرمول هایی دیگری هم استخرام کنیم مثلا از رابطه فرمول اهم دیدید حتما فرمول محاسبه ولتاژ یا جریان رو از همون فرمول بدست می آورند ولی وقتی تو برنامه نویسی بخواهیم استفاده کنیم دیگه ماشین که سر درنمیاره برعکس فلان فرمول میشه فلان پس من ایدم اینه این محاسبات و فرمول های ریاضی کلا هر فرمولی
به شکل تابع های برنامه نویسی نوشته بشوند. که یعنی ورودی های تابع مشخص بشوند و چیزی رو که به ما میده مشخص بشود این طوری منه برنامه نویسی دیگه وقتی درگیر ی پیاده سازی ی چیز پیچیده هستم ذهنم رو درگیر این معکوس کردم فرمول ها نمیکنم که فرمول های دیگری ازش دربیاد.پس مهمه این فرمول هارو به شکل سیستم در نظر بگیریم که هر سیستم ورودی داره بعد پردازش که برامون مهم نیس بعد خروجی(یعنی چیزی که به ما تحویل میده یا برامون محاسبه میکنه) ها با دانستون ورودی و خروجی دیگه “کاربرد” روشن میشه و منه برنامه نویسی دیگه هرجا لازم باشه ازش استفاده میکنم.ببخشید پر حرفی کردم ولی بنظرم اگه ریاضیات و هندسه رو از مهندسی و دانش حذف کنیم فکر نکنم چیزی تهش بمونه و این مهمه که دانشجویان ما چیزی داشته باشند تا با اون نمونه سازی و شبیه سازی کنند یا حتی تو ی چیز کاربردی ، کاربرد اون فرمول هارو ببینند که بیشتر تشویق شوند و حتی به فهمشون هم کمک میکنه، مبحث کنترل ربات های بازویی که تو صنعت هم حتما دید ی نمونه بارزش هست که فکر نکنم کسی بتونه کاربردی بودنشون رو رد کنه
ضمن عرض سلام و احترام
و تشکر بابت اینکه ما رو برای پاسخگویی به این مشکل انتخاب کردید
به شماره تماسی که در پایین صفحه در فوتر هست در تلگرام پیام بدید.
سلام محور سکانت و کسکانت بر روی دایره مثلثاتی کجا میشن؟
با سلام دوست عزیز
جنس نسبتهای مثلثاتی از جنس نسبت است سکانت که معکوس سینوس است میشود نسبت وتر به مقابل وکسکانت میشود نسبت وتر به مجاور ولی ما آنها را جزو نسبتهای اصلی حساب نمیکنیم
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
شاید حرفم یکم زشت باشه ولی ارضا شدم مطالبتون رو دیدم واقعا دمتون گرم خیلی بهم کمک کرد
با سلام وادب
خدا رو شکر که از پستهایرما نهایت استفاده رو بردید
سلام خسته نباشید. بسیار عالی بود ممنون.
با سلام وادب
ممنون از شما
با سلام و احترام خدمت دبیران گرامی و پشتیبانی های سایت :
واقعا ممنون بابت تمامی زحماتی که برای تدریس کشیدید ?
خیلی تحسین برانگیزه…!
با سلام وادب
ممنون از این همه نگاه زیبای شما که باعث دلگرمی ماهست
سلام توضیحات کاملی بود ممنون.
با سلام وادب
ممنون از نظر شما
عالی بود من بازه بین پی و منفی پی رو میخوام بدونم کجاست
عالی
سلام وقت بخیر
در کتاب سال یازدهم تجربی فصل ۴ نوشته معمولا مرکز دایره مثلثاتی مبدا مختصات است
چرا نوشته معمولا ؟؟ و چه زمانی مرکز دایره مختصات دیگه ای داره ؟؟
با سلام وادب
آفرین به دقت نظرتون
به نظر من وقتی صحبت از اندازه نسبتهای مثلثاتی و تابع مثلثاتی ورسم اون هست باید حتما مرکز دایره مثلثاتی روی مبدا مختصات بگیریم
اما وقتی صحبت از زاویه های ایتاندارد روی دایره مثلثاتی هست مرکز لزوما نباید روی مبدا باشه