آموزش ریاضی پایه نهم
نابرابری و نامعادله ریاضی نهم 📃✍️ – مجموعه جواب پیدا کن!
در درسنامۀ نابرابری و نامعادله ریاضی نهم به معرفی نابرابریها و نامعادلات میپردازیم. ابتدا تعریف نابرابری ریاضی را با هم میبینیم. در ادامه، روش نمایش نابرابری روی محور را توضیح داده و ویژگیهای نابرابری ها را بررسی میکنیم. سپس، با استفاده از نابرابریها، نامعادله را تعریف کرده و روش حل آن را بررسی میکنیم. سعی میکنیم با حل مثالهای مختلف، به درک بهتر شما از این مبحث کمک کنیم. با ما تا انتهای درسنامه همراه باشید.
نابرابری چیست؟
دو عبارت \(\Large 4\) و \(\Large 1+3\) با یکدیگر برابرند. بنابراین، با استفاده از علامت \(\Large =\) مینویسیم \(\Large 4=1+3\). به عبارت \(\Large 4=1+3\) اصطلاحاً برابری یا تساوی میگوییم. اما دو عبارت \(\Large 6\) و \(\Large 2+3\) چه طور؟ این دو عبارت با هم برابر نیستند. مینویسیم \(\Large 6>2+3\). یعنی \(\Large 6\) از \(\Large 2+3\) بزرگتر است. به عبارت \(\Large 6>2+3\)، نابرابری میگوییم. در نابرابری ها به غیر از علامتهای \(\Large <\) و \(\Large >\) از علامتهای \(\Large \leq\) و \(\Large \geq\) نیز استفاده می شود. وقتی برای دو عدد حقیقی \(\Large a\) و \(\Large b\) مینویسیم \(\Large a \leq b\)، یعنی \(\Large a\) کوچکتر یا مساوی \(\Large b\) است. یا به عبارت دیگر، \(\Large b\) بزرگتر یا مساوی \(\Large a\) است. مثلاً اگر \(\Large m\) یک عدد طبیعی باشد، آنگاه میتوانیم بنویسیم \(\Large m \geq 1\)؛ زیرا \(\Large m\) یا برابر با \(\Large 1\) است و یا از \(\Large 1\) بزرگتر است. در قسمت بعدی از درسنامۀ نابرابری و نامعادله ریاضی نهم ارتباط نابرابریها با تساویها را توضیح می دهیم.
ارتباط برابری با نابرابری
اگر \(\Large m\) و \(\Large n\) دو عدد حقیقی باشند و \(\Large m<n\) باشد، آنگاه عدد مثبتی مانند \(\Large p\) وجود دارد به طوری که \(\Large m+p=n\). مثلاً، \(\Large 2<6\) است. اگر \(\Large 2\) را با \(\Large 4\) جمع کنیم، برابر با \(\Large 6\) خواهد شد. یعنی \(\Large 2+4=6\). در این مثال، \(\Large 4\) همان عدد مثبتی است که گفتیم. به این ترتیب میتوانیم از هر نابرابری، یک برابری (تساوی) به دست آوریم.
برعکس این کار را نیز میتوانیم انجام دهیم. یعنی میتوانیم از یک تساوی، یک نابرابری به دست آوریم. مثلاً اگر \(\Large a+1=b+2\) آنگاه میتوان نتیجه گرفت که \(\Large a>b\). زیرا برای اینکه \(\Large a\) و \(\Large b\) با یکدیگر برابر شوند، \(\Large a\) باید با عدد کوچکتری جمع شود. یعنی \(\Large a\) به اندازۀ کافی بزرگ هست (البته این توضیح صرفاً برای ایجاد یک شهود کلی در شماست. اثبات اینکه \(\Large a>b\) است، با استفاده از خواصی که نابرابری ها دارند و در ادامه به آنها میپردازیم، صورت میگیرد). به قسمت بعدی از درسنامۀ نابرابری و نامعادله ریاضی نهم توجه کنید.
نمایش نابرابری روی محور
در صورتی که \(\Large a\) و \(\Large b\) اعداد حقیقی باشند و یک نابرابری به شکل \(\Large a<x<b\) داشته باشیم، میتوانیم \(\Large x\)هایی که به ازای آن، این نابرابری درست است را روی محور اعداد حقیقی به صورت زیر نشان دهیم:
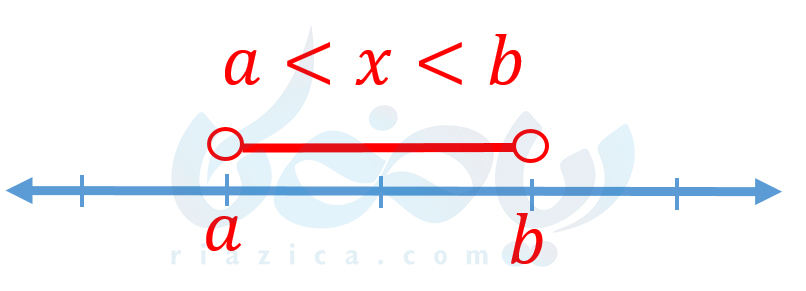
مثلاً اگر بخواهیم آن دسته از اعداد حقیقی را روی محور نمایش دهیم که در نابرابری \(\Large 1<x<4\) صدق کنند، شکل زیر را رسم میکنیم:

اگر به جای \(\Large <\) و \(\Large >\)، علامتهای \(\Large \leq\) یا \(\Large \geq\) داشته باشیم، باز هم میتوانیم نابرابری را روی محور نمایش دهیم. با این تفاوت که وقتی در کنار یک عدد یا یک عبارت، علامت \(\Large \leq\) یا \(\Large \geq\) داشته باشیم، برای آن عدد روی محور اعداد حقیقی، از دایرۀ توپُر استفاده میکنیم تا نشان دهیم علامت مساوی نیز برقرار است. برای اینکه بهتر متوجه شوید، فرض کنید میخواهیم دستهای از اعداد حقیقی را روی محور نشان دهیم که در نابرابری \(\Large 1 \leq x < 3\) صدق میکنند. در این صورت مانند شکل زیر، بین \(\Large 1\) و \(\Large 3\) یک خط رنگی کشیده و روی عدد \(\Large 1\) یک دایرۀ توپُر و روی عدد \(\Large 3\) یک دایرۀ توخالی رسم میکنیم:
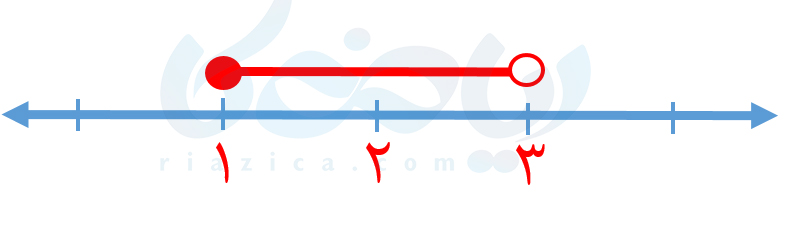
به قسمت بعدی از درسنامۀ نابرابری و نامعادله ریاضی نهم توجه کنید.
جمع کردن دو طرف نابرابری
اگر دو طرف یک نابرابری (نامساوی) را با یک عدد دلخواه یکسان جمع کنیم، نابرابری همچنان درست است. مثلاً اگر \(\Large a>b\) باشد، آنگاه \(\Large a+m>b+m\) است. به مثال بعدی دقت کنید.
مثال از درسنامۀ نابرابری و نامعادله ریاضی نهم
مثال 1: با در نظر گرفتن نابرابری \(\Large a+4>b-6\)، نابرابری \(\Large a>b-10\) را نتیجه بگیرید.
حل: همان طور که گفتیم میتوانیم دو طرف یک نابرابری را با یک عدد یکسان جمع کنیم. اگر دو طرف نابرابری \(\Large a+4>b-6\) را با عدد \(\Large -4\) جمع کنیم، آنگاه خواهیم داشت:
\(\Large a+4+(-4)>b-6+(-4)\)
\(\LARGE \Rightarrow a>b-10\)
به قسمت بعدی از درسنامۀ نابرابری و نامعادله ریاضی نهم توجه کنید.
ضرب کردن دو طرف نابرابری
در مورد ضرب دو طرف یک نابرابری در یک عدد، با توجه به مثبت یا منفی بودن آن عدد، دو حالت رخ میدهد:
- اگر دو طرف نابرابری در یک عدد مثبت ضرب شود، نابرابری همچنان برقرار است. مثلاً اگر \(\Large a>b\) و \(\Large m>0\) باشد، آنگاه \(\Large am>bm\) است.
- اگر دو طرف نابرابری در یک عدد منفی ضرب شود، جهت نابرابری عوض میشود. مثلاً اگر \(\Large a>b\) و \(\Large m<0\) باشد، آنگاه \(\Large am<bm\) است.
دقت کنید که میتوانیم دو طرف یک نابرابری را با صفر جمع کنیم، اما نمیتوانیم دو طرف یک نابرابری را در صفر ضرب کنیم. اگر دو طرف یک نابرابری را در صفر ضرب کنیم، نابرابری به تساوی \(\Large 0=0\) تبدیل میشود.
مثال از درسنامۀ نابرابری و نامعادله ریاضی نهم
مثال 2: اگر \(\Large 2y<4+2x\) باشد، ثابت کنید \(\Large y<2+x\) است.
حل: کافی است دو طرف نابرابری را در عدد \(\Large \frac{1}{2}\) ضرب کنیم:
\(\LARGE (\frac{1}{2}) \times 2y < (\frac{1}{2}) \times (4+2x)\)
برای ساده کردن عبارت سمت راست تساوی، از خاصیت پخشی استفاده میکنیم. یعنی عدد \(\Large \frac{1}{2}\) را به ترتیب در \(\Large 4\) و \(\Large 2x\) ضرب کرده و حاصل را با یکدیگر جمع میکنیم. در این صورت، نابرابری بالا به صورت زیر ساده میشود:
\(\LARGE y < \frac{1}{2} \times 4+\frac{1}{2} \times 2x\)
\(\LARGE \Rightarrow y < 2+x\)
به قسمت بعدی از درسنامۀ نابرابری و نامعادله ریاضی نهم توجه کنید.
نامعادله چیست؟
در صورتی که در یک نابرابری، یک یا چند متغیر داشته باشیم، به آن نابرابری، نامعادله میگوییم. در مثالهای 1 و 2، در واقع با یک نامعادله سروکار داشتیم. اگر در یک نابرابری، تنها یک متغیر داشته باشیم، به آن، نامعادلۀ یک مجهولی میگوییم. اگر درجۀ آن متغیر، یک باشد، به آن، نامعادلۀ یک مجهولی درجۀ اول میگوییم. مثلاً، نابرابریهای \(\Large x<3\) و \(\Large 2y-4<5\)، نامعادلههای یک مجهولی درجۀ اول هستند.
مجموعۀ جواب نامعادله
همان طور که گفتیم، در یک نامعادلۀ یک مجهولی، یک متغیر وجود دارد. اگر به جای آن متغیر، یک عدد قرار دهیم، یا نامعادله تبدیل به یک نابرابری درست میشود یا تبدیل به یک نابرابری غلط. مثلاً، به جدول زیر نگاه کنید؛ به جای متغیر \(\Large x\) در نامعادلۀ \(\Large 3x+2>8\)، مقدارهای \(\Large 1\) و \(\Large 2\) و \(\Large 3\) و \(\Large 4\) را قرار دادیم:
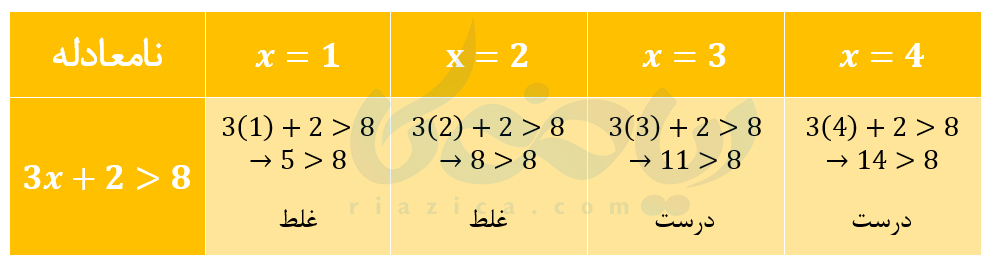
همان طور که میبینید، نامعادلۀ داده شده به ازای \(\Large x=3\) و \(\Large x=4\) به نابرابری درست و به ازای \(\Large x=1\) و \(\Large x=2\) به نابرابری غلط تبدیل شده است. به مجموعۀ مقادیری که به ازای آنها، نامعادله تبدیل به نابرابری درست میشود، مجموعۀ جواب نامعادله میگوییم. بنابراین در این مثال، اعداد \(\Large 3\) و \(\Large 4\) در مجموعۀ جواب نامعادله قرار دارند. البته به غیر از اعداد \(\Large 3\) و \(\Large 4\)، اعداد حقیقی دیگری نیز وجود دارند که در معادله صدق میکنند. در قسمت بعدی از درسنامۀ نابرابری و نامعادله ریاضی نهم روش به دست آوردن مجموعۀ جواب یک نامعادله را بررسی میکنیم.
روش یافتن مجموعۀ جواب نامعادله درجه اول
برای اینکه مجموعۀ جواب یک نامعادلۀ یک مجهولی درجه اول را به دست آوریم، باید نامعادله را به صورتی ساده کنیم که در یک سمت آن، متغیر نامعادله با ضریب یک و در سمت دیگر، عددی ثابت قرار داشته باشد. اما چه طور میتوان یک نامعادله را ساده کرد؟ دقیقاً همان طور که در مثالهای 1 و 2 این کار را کردیم. یعنی اعداد یا عباراتی را با دو طرف تساوی جمع و یا در دو طرف تساوی ضرب میکنیم. فقط در مورد ضرب باید حواسمان به نکاتی که گفتیم باشد. یعنی اگر دو طرف نابرابری را در یک عدد منفی ضرب کردیم، جهت نابرابری عوض میشود.
به طور مثال، برای اینکه نامعادلۀ \(\Large x+4<5\) را به صورتی ساده کنیم که در آن متغیر \(\Large x\) با ضریب \(\Large 1\) در یک طرف نامعادله قرار گرفته و یک عدد ثابت در سمت دیگر آن قرار داشته باشد، کافی است دو طرف نامعادله را با عدد \(\Large -4\) جمع کنیم. در این صورت داریم:
\(\LARGE x+4+(-4)<5+(-4)\)
\(\LARGE \Rightarrow x<1\)
در نتیجه، مجموعۀجواب نامعادلۀ \(\Large x+4<5\) برابر است با مجموعۀ تمام اعداد حقیقی کوچکتر از یک. میتوانیم مجموعۀ جواب را با استفاده از نمادهای ریاضی نیز به صورت زیر نمایش دهیم:
\(\LARGE D=\{x \in \mathbb{R}| x<1\}\)
مجموعۀ \(\Large D\)، مجموعۀ جواب نامعادله است. البته در درسنامه آموزش حل نامعادله میآموزیم چگونه با استفاده از تعیین علامت نامعادلات درجات بالاتر وگویا را حل کنیم .به مثالهای زیر از درسنامۀ نابرابری و نامعادله ریاضی نهم توجه کنید.
مثال از درسنامۀ نابرابری و نامعادله ریاضی نهم
مثال 3: مجموعۀ جواب نامعادلۀ \(\Large 3x-2 \leq 7\) را به دست آورید (در این درسنامه هر جا میگوییم مجموعۀ جواب، منظورمان مجموعۀ جواب در اعداد حقیقی است).
حل: باید طوری نامعادله را ساده کنیم که \(\Large x\) با ضریب \(\Large 1\) در یک طرف قرار بگیرد. ابتدا دو طرف نامعادله را با عدد \(\Large 2\) جمع میکنیم:
\(\LARGE 3x-2+2 \leq 7+2\)
\(\LARGE \Rightarrow 3x \leq 9\)
حال برای اینکه ضریب \(\Large x\) برابر با \(\Large 1\) شود، دو طرف نامعادله را در \(\Large \frac{1}{3}\) ضرب میکنیم:
\(\LARGE \frac{1}{3} \times 3x \leq \frac{1}{3} \times 9\)
\(\LARGE \Rightarrow x \leq 3\)
در نتیجه مجموعه جواب نامعادله برابر است با:
\(\LARGE D=\{x \in \mathbb{R}| x\leq 3 \}\)
به مثال زیر از درسنامۀ نابرابری و نامعادله ریاضی نهم توجه کنید.
مثال از حل نامعادله
مثال 4: مجموعۀ جواب نامعادلۀ \(\Large \frac{y+2}{6}+4>\frac{5}{3}\) را به دست آورید.
حل: دو عبارت کسری داریم که مخرج یکی برابر با \(\Large 3\) و مخرج دیگری برابر با \(\Large 6\) است. اگر دو طرف نامعادله را در ک.م.م دو عدد \(\Large 3\) و \(\Large 6\) ضرب کنیم، مخرجها ساده میشوند. ک.م.م دو عدد \(\Large 3\) و \(\Large 6\) برابر با \(\Large 6\) است، بنابراین دو طرف نامعادله را در \(\Large 6\) ضرب میکنیم:
\(\LARGE 6 \times (\frac{y+2}{6}+4)>6 \times \frac{5}{3}\)
\(\LARGE \Rightarrow (y+2)+24 > 10\)
\(\LARGE \Rightarrow y+26 > 10\)
حال کافی است دو طرف نامعادله را با عدد \(\Large -26\) جمع کنیم تا در سمت چپ نامعادله، تنها \(\Large y\) باقی بماند:
\(\Large y+26+(-26) > 10+(-26)\)
\(\LARGE \Rightarrow y> -16\)
در نتیجه، مجموعۀ جواب نامعادله برابر است با:
\(\LARGE D=\{y \in \mathbb{R}| y> -16 \}\)
مثال از درسنامۀ نابرابری و نامعادله ریاضی نهم
مثال 5: اگر \(\Large x\) و \(\Large y\) مثبت باشند و \(\Large x^2<y^2\)، ثابت کنید \(\Large x<y\).
حل: اگر به دو طرف نابرابری داده شده، عبارت \(\Large -y^2\) را اضافه کنیم، خواهیم داشت:
\(\LARGE x^2-y^2<0\)
از طرفی، طبق اتحاد مزدوج میتوانیم عبارت بالا را به صورت زیر بنویسیم (درسنامۀ تجزیه ریاضی نهم را مرور کنید):
\(\LARGE (x-y)(x+y)<0\)
چون در صورت سوال گفته شده که \(\Large x\) و \(\Large y\) مثبت هستند، بنابراین \(\Large x+y\) نیز مثبت است. در نتیجه، با توجه به نابرابری بالا، \(\Large x-y\) منفی است. پس داریم:
\(\LARGE x-y<0\)
اگر به دو طرف نامساوی بالا، \(\Large y\) را اضافه کنیم، نابرابری زیر به دست میآید:
\(\LARGE x<y\)
مثال از درسنامۀ نابرابری و نامعادله ریاضی نهم
مثال 6: هزینۀ ارسال درون شهری یک بستۀ پستی با وزن \(\Large 5\) کیلوگرم و به صورت سفارشی برابر با \(\Large 10\) هزار تومان است. اگر در این بسته یک کتاب به وزن \(\Large 300\) گرم داشته باشیم، حداکثر چند دفترچه که وزن هر کدام \(\Large 200\) گرم است میتوانیم در بسته قرار دهیم تا هزینۀ ارسال بسته بیشتر از \(\Large 10\) هزار تومان نشود.
حل: برای اینکه هزینۀ ارسال بسته بیشتر از \(\Large 10\) هزار تومان نشود، وزن بسته باید حداکثر \(\Large 5\) کیلوگرم باشد. اگر تعداد دفترچهها را با \(\Large x\) نشان دهیم، داریم:
\(\LARGE 300+200x<5000\)
اگر \(\Large 300\) را از دو طرف نامعادلۀ بالا کم کنیم، عبارت زیر به دست میآید:
\(\LARGE 200x<4700\)
در صورتی که دو طرف نامعادلۀ بالا را بر \(\Large 200\) تقسیم کنیم، خواهیم داشت:
\(\LARGE x<\frac{4700}{200}\)
\(\LARGE x<23.5\)
بنابراین حداکثر \(\Large 23\) دفترچه میتوانیم ارسال کنیم.
ویدیو از نامعادله ونابرابری ریاضی نهم
در این ویدیو با حل چند مثال نامعادله درجه اول توضیح داده شده است
زنگ آخر کلاس نابرابری و نامعادله ریاضی نهم
در درسنامهای که از ریاضی نهم خواندیم، نابرابری ها را معرفی کرده و نحوۀ نمایش آنها روی محور را بررسی کردیم. گفتیم در صورتی که در نابرابری، یک یا چند متغیر وجود داشته باشد، به آن نابرابری، نامعادله میگوییم. همان طور که دیدید با جمع دو طرف نامعادله با یک عدد یا ضرب دو طرف آن در یک عدد و یا ترکیبی از این دو عمل، نامعادله را ساده کرده و مجموعۀ جواب نامعادله را به دست آوردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





salam kheli mmanon az sait khobeton tamam mataleb mofid va kamel bood enshaAlla ke mofagh bashid tashakor.
با سلام وروز به خیر
ممنون از توجه شما ونظرات مفیدتون
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
اینجا ایران هست برادر
فهمیدیم توهم اینگیلیسی بلدی
با تشکر ??
?عالی بوددددددددددددددددددددددددد??????
سلامت بااااااااااااااااااشییییییییییییییییید ? ?? ?? ?? ?? ?
ببخشید اگه ضریب مجهول منفی باشه چطور میشه حل کرد ؟
با سلام وعرض ادب
مثل مثبت فقط وقتی طرفبن به ضریب مجهول تقسیم میشند جهت نامعادله عوض میشه
سلام وقت شما بخیر
زمانی که عبارت وسط پارامتری باشه و باید تنهاش کنیم ، طرفین چه تغییری می کنن؟
باسلام وادب
ابتدا اگه جمله مجهول دار با عدی جمع یا کم شده طرفین(سه طرف) رو برعکس با اون عددکم یا جمع میکنیم بعد طرفین رو به ضریب مجهول تقسیم میکنیم تا وسط مجهول ودوطرف عدد باقی بمونه
https://riazica.com/solving-inequalities/ به این پست مراجعه کنید هم جواب خودتون رو میگیرید
سلام ببخشید اگر عبارت یا عددی رو از یک طرف نامعادله به طرف دیگر منتقل کنیم جهت علامت عوض میشه؟
پاسخ داده شد
سلام ببخشید اگر عبارت یا عددی رو از یک سمت معادله به سمت دیگه منتقل کنیم جهت علامت عوض میشه؟
با سلام وعرض ادب
در نامعادله فقط اگر دوطرف در عدد منفی ضرب وتقسیم شود جهت آن عوض کیشود اگه عددی رو از طرفی به طرف دیگر ببریم فقط علامت آن عدد عوض مبشود
سلام استاد خیلی خیلی سپاسگذارم بابت این تدریس خیلی عالی و فوق العاده تون،یه دنیا ممنون، انشالله همیشه شاد و سلامت و موفق باشید.❤❤❤❤❤❤❤❤❤??????????????????????????
با سلام واحترام
خوشحالیم وانرژی میگیریم از اینهمه پیامهای خوب شما
سپاس
سلام ببخشید میخواستم بدونم وقتی دو طرف نامعادله رو به توان دو برسانم جهت عوض میشه؟؟؟
با سلام وادب
فقط وقتی میتونید دو طرف رو به توان دوبرسونید که بدونید دو طرف مثبت هستن واحتیاجی به تغییر جهت نداره
عالی و جامع و کامل?
سلام خیلی ممنون عالی بود بسیار مفید و قابل درک بود.
با سلام و ادب
ممنون وخرسندیم که به هدف خودمون رسیدیم
بهترین دسته بندی و کامل ترین شیوه بیان این مبحث بود،درود بر شما
با سلام
ممنون از نگاه شما
سلام و خسته نباشید .
ممنون بابت این تدریس عالیتون امروز قرار بود این مبحث رو درس بدن و هیچی هم بلد نبودم و با نگاه کردن به این تدریس همسوی رو یاد گرفتم ❤️
سلام ممنون از نظر لطف شما خدا رو شاکریم که مفید بوده
سلام
اگه بخوایم یه عدد رو از یه طرف نا معادله ببریم یه طرف دیگه باید چی کار کنیم؟
با سلام مثل معادله فقط علامتش عوض میشه