معرفی عبارت گویا نهم 🔤➗ – مفهومی و کاربردی!

در درسنامهٔ معرفی عبارت گویا نهم ابتدا منظورمان از عبارت گویا را بیان می‌کنیم. سپس، به بررسی مطالب زیر می‌پردازیم:

• مقدار عددی عبارت‌های گویا
• یک عبارت گویا به ازای چه مقادیری تعریف نشده است؟
• ساده کردن عبارت‌های گویا
• عبارات گویا و تناسب

از آنجاییکه آشنایی با چند جمله ای ها در این درسنامه اهمیت ویژه‌ای دارد، توصیه می‌کنیم قبل از شروع مطالعهٔ درسنامهٔ معرفی عبارت گویا نهم ، درسنامهٔ عبارت های جبری نهم را مرور کنید. با ما تا انتها همراه باشید.

عبارت گویا چیست؟

تعریف: به کسری که صورت و مخرج آن چندجمله‌ای باشد، عبارت گویا می‌گوییم.

باید یادآوری کنیم که چندجمله‌ای ها از یک‌جمله‌ای ها تشکیل شده‌اند. یک‌جمله‌ای‌ها نیز عباراتی جبری هستند که توان متغیر در آن‌ها صحیح بوده و ضرایب، اعداد حقیقی هستند. با توجه به تعریف، عبارت‌هایی مثل \(\Large \frac{x+2}{2x-8}\) و یا \(\Large \frac{4x+\sqrt{5}}{2b-a}\)، عبارت‌های گویا هستند. زیرا صورت و مخرجشان یک چند‌جمله‌ای است. حتی اعداد گویا که خیلی قبل با آن‌ها آشنا شدیم نیز، حالت خاصی از عبارات گویا هستند. زیرا هر عدد گویا برابر است با کسری که صورت و مخرج آن، عدد صحیح است. هر عدد صحیح نیز، یک یک‌جمله‌ای از درجهٔ صفر است. یک‌جمله‌ای‌ها نیز حالت خاصی از چند‌جمله‌ای ها هستند. بنابراین اعداد گویا هم حالت خاصی از عبارات گویا هستند. به مثال بعدی از درسنامهٔ معرفی عبارت گویا نهم توجه کنید.

مثال از عبارت‌های گویا

مثال 1: کدام یک از عبارت‌های زیر گویا هستند؟

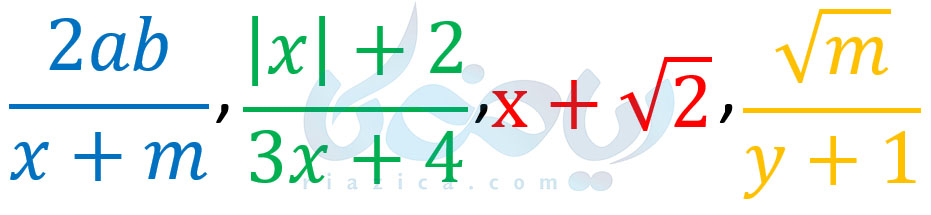
حل: عبارت \(\Large \frac{2ab}{x+m}\) گویاست؛ زیرا هم صورت و هم مخرج آن، چندجمله‌ای است. دقت کنید که لزومی ندارد که عبارت گویا فقط یک متغیر داشته باشد. عبارت \(\Large \frac{|x|+2}{3x+4}\) گویا نیست؛ دلیل آن هم وجود قدر‌مطلق در صورت کسر است. عبارت \(\Large x+\sqrt{2}\) گویا است؛ در واقع این عبارت& کسری است که مخرج آن برابر با \(\Large 1\) و صورت آن چندجمله‌ای است. مورد آخر، یعنی عبارت \(\Large \frac{\sqrt{m}}{y+1}\) گویا نیست؛ زیرا توان متغیر باید صحیح باشد. در صورت کسر، توان متغیر \(\Large m\) برابر با \(\Large \frac{1}{2}\) است. دقت کنید، توان اعداد ثابت می‌تواند غیر صحیح باشد. مثلاً اگر در صورت عبارت \(\Large \frac{\sqrt{m}}{y+1}\) به جای \(\Large m\) یک عدد ثابت داشتیم، عبارت گویا می‌شد. به قسمت بعدی از درسنامهٔ معرفی عبارت گویا نهم توجه کنید.

مقدار عددی عبارت‌های گویا

در درسنامهٔ عبارت های جبری نهم دیدیم که چگونه می‌توان مقدار عددی یک چندجمله‌ای را به دست آورد. اگر در عبارات گویا، مقدار عددی چندجمله‌ای‌های صورت و مخرج را به دست آوریم، مقدار عددی کل عبارت گویا با تقسیم صورت بر مخرج به دست می‌آید. به طور مثال اگر در عبارت جبری \(\Large \frac{x+2}{x-1}\) به جای متغیر \(\Large x\) عدد \(\Large 2\) را قرار دهیم، مقدار عددی عبارت جبری برابر با \(\Large \frac{2+2}{2-1}\) که همان \(\Large 4\) است می‌شود. برای اینکه بهتر متوجه شوید، به مثال بعدی از درسنامهٔ معرفی عبارت گویا نهم توجه کنید.

مثال از مقدار عددی عبارت‌های گویا

مثال 2: مقدار عددی عبارت گویای \(\Large \frac{x+5}{x+1}\) را به ازای \(\Large x=1\) و \(\Large x=0\) و \(\Large x=\frac{1}{3}\) به دست آورید.

حل: کافی است در عبارت گویای \(\Large \frac{x+5}{x+1}\) به جای \(\Large x\) مقادیر \(\Large 1\) و \(\Large 0\) و \(\Large \frac{1}{3}\) را قرار دهیم.  مقدار عددی عبارت \(\Large \frac{x+5}{x+1}\) به ازای مقادیر خواسته شده را در جدول زیر نشان داده‌ایم:

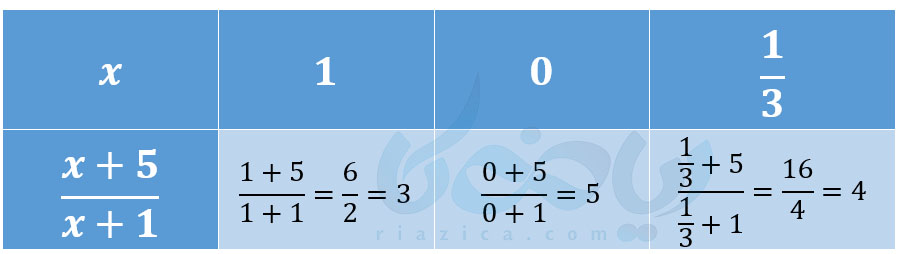
ساده کردن عبارت های گویا

همان طور که می‌توانستیم کسرها را ساده کنیم، می‌توانیم عبارات گویا را نیز ساده کنیم. برای ساده کردن کسرها و اعداد گویا کافی بود در صورت و مخرج کسر، یک عامل مشترک پیداکنیم. به طور مثال برای ساده کردن کسر \(\Large \frac{4}{18}\) عملیات زیر را انجام می‌دادیم:

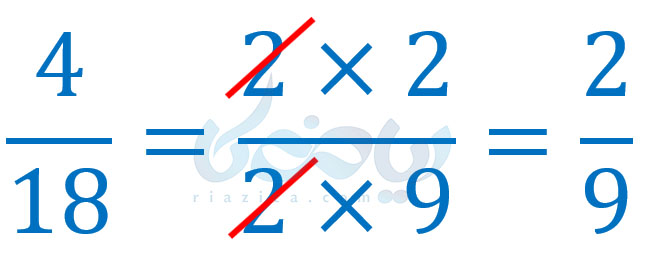
در واقع مفهوم خط زدن عدد \(\Large 2\) در عبارت بالا، همان تقسیم صورت و مخرج کسر بر عدد \(\Large 2\) است. به طور کلی می‌توانیم صورت و مخرج هر کسر را بر یک عدد غیر صفر تقسیم کنیم. مشابه همین کار را برای عبارات گویا نیز می‌توان انجام داد. یعنی صورت و مخرج هر عبارت گویا را می‌توان بر یک عبارت غیرصفر تقسیم کرد. دقت کنید، گاهی لازم است ابتدا صورت و مخرج یک عبارت گویا را با استفاده از مطالبی که در درسنامهٔ تجزیه ریاضی نهم آموختیم، تجزیه کرده و سپس آن را ساده کنیم. برای اینکه بهتر متوجه شوید، به مثال‌های بعدی از درسنامهٔ معرفی عبارت گویا نهم توجه کنید.

مثال از ساده کردن عبارت‌های گویا

مثال 3: عبارت گویای \(\Large \frac{x^2+4x+4}{x^2+5x+6}\) را ساده کنید.

حل: ابتدا صورت کسر را با استفاده از اتحاد مربع دو جمله‌ای و مخرج آن را با استفاده از اتحاد جمله مشترک تجزیه می‌کنیم (در صورتی که تجزیه با استفاده از این اتحادها را فراموش کرده‌اید، حتما درسنامهٔ تجزیه ریاضی نهم را مرور کنید):

\(\LARGE \frac{x^2+4x+4}{x^2+5x+6}=\frac{(x+2)^2}{(x+2)(x+3)}\)

\(\LARGE =\frac{(x+2)(x+2)}{(x+2)(x+3)}\)

حال عبارت \(\Large (x+2)\) را از صورت و مخرج کسر ساده می‌کنیم:

\(\LARGE \frac{(x+2)(x+2)}{(x+2)(x+3)}=\frac{x+2}{x+3}\)

به مثال بعدی از درسنامهٔ معرفی عبارت گویا نهم توجه کنید.

مثال 4: عبارت گویای \(\Large \frac{x^2-9}{2x^2-6x}\) را ساده کنید.

حل: صورت کسر را با استفاده از اتحاد مزدوج و مخرج آن را با استفاده از فاکتورگیری، تجزیه می‌کنیم:

\(\LARGE \frac{x^2-9}{2x^2-6x}=\frac{(x-3)(x+3)}{2x(x-3)}\)

همان طور که می‌بینید، عبارت \(\Large (x-3)\) در صورت و مخرج کسر مشترک است و می‌توانیم آن را ساده کنیم:

\(\LARGE \frac{(x-3)(x+3)}{2x(x-3)}=\frac{x+3}{2x}\)

به مثال بعدی از درسنامهٔ معرفی عبارت گویا نهم توجه کنید

مثال از ساده کردن عبارت‌های گویا

مثال 5: عبارت گویای \(\Large \frac{x^2+7x+10}{x^2-25}\) را ساده کنید.

حل: صورت کسر را با استفاده از اتحاد جمله مشترک و مخرج آن را با استفاده از اتحاد مزدوج، تجزیه می‌کنیم:

\(\LARGE \frac{x^2+7x+10}{x^2-25}\)

\(\LARGE =\frac{(x+5)(x+2)}{(x+5)(x-5)}\)

همان طور که می‌بینید، عبارت \(\Large (x+5)\) در صورت و مخرج کسر مشترک است و می‌توانیم آن را ساده کنیم:

\(\LARGE \frac{(x+5)(x+2)}{(x+5)(x-5)}\)

\(\LARGE =\frac{x+2}{x-5}\)

به مثال بعدی از درسنامهٔ معرفی عبارت گویا نهم توجه کنید

یک عبارت گویا به ازای چه مقادیری تعریف نشده؟

در صورتی که مخرج یک عبارت گویا برابر با صفر شود، آن عبارت گویا تعریف نشده است. به طور مثال مخرج عبارت گویای \(\Large \frac{2x+6}{x-3}\) به ازای \(\Large x=3\) برابر با صفر می‌شود؛ در این صورت می‌گوییم عبارت گویای \(\Large \frac{2x+6}{x-3}\) به ازای \(\Large x=3\) تعریف نشده است. به مثال‌های بعدی از درسنامهٔ معرفی عبارت گویا نهم توجه کنید.

مثال از درسنامهٔ معرفی عبارت گویا نهم

مثال 6: عبارت گویای \(\Large \frac{3x+2}{(x-1)(x+3)}\) به ازای چه مقادیری از \(\Large x\) تعریف نشده است؟

حل: باید ریشه‌های مخرج را پیدا کنیم (منظور از ریشه‌های مخرج، همان اعدادی است که به ازای آن‌ها مخرج برابر با صفر می‌شود). برای این کار، مخرج کسر را مساوی با صفر قرار می‌دهیم:

\(\LARGE (x-1)(x+3)=0\)

همان طور که می‌بینید، حاصل ضرب \(\Large (x-1)\) در \(\Large (x+3)\) برابر با صفر شده است. بنابراین یا یکی از آن‌ها و یا هر دوی آن‌ها برابر با صفر هستند. پس داریم:

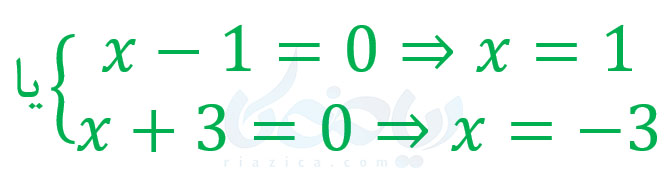
در نتیجه، عبارت گویای \(\Large \frac{3x+2}{(x-1)(x+3)}\) به ازای \(\Large x=1\) و \(\Large x=-3\) تعریف نشده است.

برای علاقه‌مندان: همان طور که در حل این مثال دیدید، از آنجاییکه حاصل ضرب دو عبارت برابر با صفر شده بود، نتیجه گرفتیم که حداقل یکی از آن‌ها صفر است. در ریاضیات می‌توان ساختارهایی یافت که دارای چنین خاصیتی نباشند. اگر مایل بودید می‌توانید در مورد این خاصیت، دامنه‌های صحیح و همجنین شمارنده‌های صفر تحقیق کنید.

به مثال‌ بعدی از درسنامهٔ معرفی عبارت گویا نهم توجه کنید.

مثال از درسنامهٔ معرفی عبارت گویا نهم

مثال 7: عبارت گویای \(\Large \frac{x+3}{x^2-4}\) به ازای چه مقادیری از \(\Large x\) تعریف نشده است؟

حل: مانند مثال قبل باید ریشه‌های مخرج کسر را پیدا کنیم. برای این کار ابتدا مخرج کسر را با استفاده از اتحاد مزدوج که در درسنامهٔ تجزیه ریاضی نهم خواندیم، تجزیه می‌کنیم:

\(\LARGE \frac{x+3}{x^2-4}=\frac{x+3}{(x-2)(x+2)}\)

حال مخرج کسر را برابر با صفر قرار می‌دهیم تا ریشه‌های مخرج مشخص شوند:

\(\LARGE (x-2)(x+2)=0 \)

\(\LARGE \Rightarrow x=2\), \(\LARGE -2\)

در نتیجه، عبارت گویای \(\Large \frac{x+2}{x^2-4}\) به ازای \(\Large x=2\) و \(\Large x=-2\) تعریف نشده است. به قسمت بعدی از درسنامهٔ معرفی عبارت گویا نهم توجه کنید.

عبارات گویا و تناسب

اگر دو عبارت گویا را با یکدیگر مساوی قرار دهیم، یک تناسب گویا تشکیل می‌شود. به طور مثال، \(\Large \frac{x+2}{x-3}=\frac{(x+2)(x+1)}{(x-3)(x+1)}\) یک تناسب است. اگر صورت و مخرج کسر \(\Large \frac{x+2}{x-3}\) را در عبارت \(\Large (x+1)\) ضرب کنیم، کسر \(\Large \frac{(x+2)(x+1)}{(x-3)(x+1)}\) به دست می‌آید. در دو مثال بعدی، دو تناسب را حل می‌کنیم.

مثال از عبارت گویا و تناسب

مثال 8: در تناسب \(\Large \frac{x-5}{x+1}=\frac{A}{x^2-1}\) به جای \(\Large A\) چه عبارتی قرار دهیم؟

حل: عبارت \(\Large x^2-1\) را می‌توان با استفاده از اتحاد مزدوج تجزیه کرد. یعنی داریم:

\(\LARGE \frac{x-5}{x+1}=\frac{A}{(x+1)(x-1)}\)

بنابراین مخرج کسر سمت چپ، در \(\Large x-1\) ضرب شده است. پس، صورت آن نیز باید در \(\Large x-1\) ضرب شود. بنابراین، عبارت \(\Large A\) برابر است با:

\(\LARGE A=(x-5)(x-1)\)

به مثال بعدی از درسنامهٔ معرفی عبارت گویا نهم توجه کنید.

مثال از عبارت گویا و تناسب

مثال 9: در تناسب \(\Large \frac{A \times (y+3)}{(y+1)(y+3)}=2y-1\) به جای \(\Large A\) چه عبارتی قرار دهیم؟

حل: ابتدا عبارت \(\Large y+3\) را از صورت و مخرج کسر سمت چپ ساده می‌کنیم تا تناسب داده شده به صورت زیر ساده شود:

\(\LARGE \frac{A}{y+1}=2y-1\)

در سمت راست تساوی یک کسر داریم که مخرج آن برابر با \(\Large 1\) است. در واقع تناسب بالا به صورت زیر است:

\(\LARGE \frac{A}{y+1}=\frac{2y-1}{1}\)

مخرج کسر سمت راست، در عبارت \(\LARGE (y+1)\) ضرب شده تا مخرج کسر سمت چپ به دست بیاید. بنابراین صورت کسر سمت راست نیز باید در عبارت \(\LARGE (y+1)\) ضرب شود تا صورت کسر سمت چپ به دست بیاید. بنابراین، عبارت \(\Large A\) برابر است با:

\(\LARGE A=(2y-1)(y+1)\)

در ادامه میتونی درسنامه تابع گویا رو برای یادگیری بیشتر مطالعه کنی

زنگ آخر کلاس معرفی عبارت گویا نهم

در درسنامه‌ای که از ریاضی نهم خواندیم، ابتدا منظور از عبارت گویا را بیان کردیم. سپس مقدار عددی عبارت‌های گویا را به ازای مقادیر مختلف به دست آورده و آن‌ها را ساده کردیم. همان طور که دیدید، حاصل یک عبارت گویا به ازای مقادیری که مخرج را صفر می‌کند، تعریف نشده است. در انتها نیز، با برابر قرار دادن عبارات گویا، تناسب تشکیل دادیم.

ما در ریاضیکا آماده‌ی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با این مبحث دارید، در دیدگاه‌ها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند ‌داد.