آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد می‌گیرید

احتمالی یا حتمی؟ مسأله این است!!! شانس در ریاضیات یعنی چه؟ در قرعه‌کشی بزرگی با یک میلیون شرکت‌کننده چقدر احتمال برنده شدن شما وجود دارد؟ در آموزش احتمال هشتم از مجموعه آموزش ریاضی پایه هشتم قصد داریم احتمال رخ دادن یک پیشامد و حالت‌های هم‌شانس را با هم یاد بگیریم.

همچنین از دو روش کاربردی برای بررسی کل حالت‌های ممکن در یک پیشامد – یعنی نمودار درختی و جدول نظام‌دار- را برای حل سؤالات استفاده کنیم.

آمار و احتمال در زندگی روزمره بسیار مورد استفاده قرار می‌گیرد؛ با استفاده از داده‌های آماری و بررسی آن‌ها و با درک مفاهیمی که در احتمال هشتم یاد می‌گیریم‌، می‌توانیم وقایعی را پیش‌بینی کنیم. پیش‌بینی آب و هوا و بارندگی یکی از مواردی است که از این علم استفاده می‌کند.

احتمال رخ دادن هر پیشامد

تعریف احتمال

احتمال رخ دادن هر پیشامد، نسبت تعداد حالت‌های مطلوب به تعداد همه حالت‌های ممکن است.

تذکر: منظور از حالت‌های مطلوب، حالاتی است که مورد بررسی بوده و می‌خواهیم احتمال آن را اندازه‌گیری کنیم. به عنوان مثال اگر در یک کیسه 3 عدد توپ هم‌شکل با رنگ‌های سبز، آبی و قرمز وجود داشته باشد، احتمال بیرون آمدن توپ سبز رنگ، \( \Large \frac {1}{3} \) است. در این مثال، ممکن است سه حالت اتفاق بیفتد:

1. توپ سبز رنگ خارج شود؛ یا
2. توپ آبی رنگ خارج شود؛ یا
3. توپ قرمز رنگ خارج شود.

پس کل حالت‌های ممکن برابر است با 3. همچنین می‌خواهیم احتمال بیرون آمدن توپ سبز رنگ را بدست آوریم. پس حالت مطلوب ما بیرون آمدن توپ سبز رنگ است که برابر است با 1.

حالت‌های هم‌شانس

یکی دیگر از مواردی که باید در آموزش احتمال هشتم بررسی کنیم، حالت‌های هم‌شانس است. حالت‌هایی که احتمال رخ دادن آن‌ها با هم برابر باشد (یعنی همه حالت‌ها شانس یکسانی برای اتفاق افتادن داشته باشند). در مثال گفته شده در قسمت قبل، احتمال بیرون آمدن هر سه توپ با هم برابر است (\( \Large \frac {1}{3} \)). پس بیرون آمدن این سه توپ، حالت‌های هم‌شانس هستند.

مثال 1: در کیسه زیر، همه حالت‌های هم‌شانس را مشخص کنید.

حل 1:

برای مشخص کردن حالت‌های هم‌شانس، ابتدا باید احتمال هر پیشامد را بدست آوریم و سپس مقادیر برابر را تعیین کنیم. کل حالت‌های ممکن برابر با 4 است، چون 4 گوی داریم. همچنین گوی سبز به 1 حالت، گوی قرمز به 2 حالت و گوی زرد به 1 حالت می‌توانند از کسیه خارج شوند.

پس طبق تعریف، احتمال بیرون آمدن گوی سبز، قرمز و زرد به ترتیب برابر است با: \( \Large \frac {1}{4} \) ، \( \Large \frac {2}{4} \) و \( \Large \frac {1}{4} \) . پس بیرون آمدن گوی سبز و زرد حالت‌های هم‌شانس هستند، چون احتمال این دو برابر است.

– تموم شد؟    – نه!

یک حالت دیگر هم داریم که نیاز به دقت دارد. احتمال بیرون آمدن هر یک از گوی‌ها برابر با \( \Large \frac {1}{4} \) است (رنگ را در نظر نگیرید)؛ طبق حالات زیر (دو گوی قرمز داریم که شماره یکی را 1 و شماره دیگری را 2 گذاشته‌ایم):

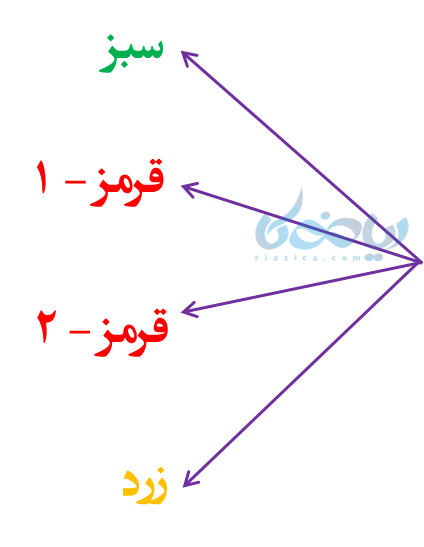
پس بیرون آمدن هر یک از چهار گوی نیز یکی از حالت‌های هم‌شانس است.

نکات تکمیلی در آموزش احتمال هشتم

پیش از ادامه مبحث آموزش احتمال هشتم نیاز است که نکاتی تکمیلی را باهم بررسی کنیم. رابطهٔ گفته شده برای احتمال رخ دادن هر پیشامد، نکاتی دارد که به شرح ذیل هستند:

1. تکرار یک آزمایش تأثیری روی نتایج بعدی ندارد. مثلاً اگر 100 بار یک سکه را انداخته باشیم و هر 100 بار «رو» آمده باشد، بار 101اُم باز هم شانس «رو» یا «پشت» آمدن برابر است.
2. احتمال رخ دادن یک پیشامد، برابر با صفر، یک یا عددی بین صفر و یک است.
3. مجموع احتمال‌ها در یک مسأله، همواره برابر با 1 است. بنابراین:

انواع احتمال در آموزش احتمال هشتم

الف) حتمی (قطعی)

پیشامدی که حتماً اتفاق می‌افتد؛ در این حالت، احتمال برابر با 1 می‌باشد. (\( \Large p=1 \))

ب) غیرممکن

پیشامدی که هرگز اتفاق نمی‌افتد؛ در این حالت، احتمال برابر با 0 می‌باشد. (\( \Large p=0 \))

ج) ممکن

احتمال هر پیشامدی که نه قطعاً اتفاق می‌افتد و نه غیرممکن است، عددی بین 0 و 1 است. (\( \Large 0<p<1 \)) (چون طبق رابطه اول درس، هیچ‌گاه تعداد حالت‌های مطلوب از تعداد حالت‌های ممکن بیشتر نمی‌شود.)

حل چند مثال برای فهم بهتر احتمال هشتم

مثال 2: در لیگ برتر والیبال، احتمال قهرمانی کاله آمل، سایپا و پیکان به ترتیب برابر با \( \large \frac {1}{5} \) ، \( \large \frac {1}{5} \) و \( \large \frac {2}{5}  \) است. احتمال قهرمانی سایر تیم‌های لیگ روی هم چقدر است؟

حل 2:

مجموع احتمال ها در یک مسأله همواره برابر با 1 است. مجموع احتمال قهرمانی سایر تیم‌ها را \( \Large x \)  نام‌گذاری می‌کنیم؛ بنابراین داریم:

\( \LARGE \frac {1}{5} + \frac {1}{5} + \frac {2}{5} + x = 1 \)

\( \LARGE \frac {4}{5} + x = 1 \)

\( \LARGE x = 1- \frac {4}{5} = \frac {1}{5}   \)

مثال 3: کمان‌های یک دایره به شعاع 10 سانتی‌متر را به چند بخش تقسیم و این کمان‌ها را رنگ کرده‌ایم. احتمال قرمز بودن این کمان‌ها \( \large \frac {1}{10} \) است. احتمالاً چه طول کمانی از دایره به رنگ‌های دیگر است؟

حل 3:

احتمال قرمز نبودن کمان‌ها (NR) را از رابطهٔ (احتمال رخ ندادن) بدست می‌آوریم (در این رابطه R، احتمال قرمز بودن است):

\( \LARGE R+NR=1 \)

\( \LARGE NR=1-\frac {1}{10} \)

\( \LARGE NR=\frac {9}{10} \)

پس احتمال قرمز نبودن کمان‌ها \( \large \frac {9}{10} \) است. حال برای محاسبه طول کمان‌ها (S) کافی است \( \large \frac {9}{10} \) محیط دایره را محاسبه کنیم:

\( \LARGE S=\frac {9}{10} * (2 \pi r) \)

\( \LARGE S=\frac {9}{10} * (20 \pi) \)

\( \LARGE S=18 \pi \)

مثال ترکیبی با مبحث اعداد اول

مثال 4: روی یک چرخنده، اعداد 31 تا 60 نوشته شده است. چرخنده را می‌چرخانیم، احتمال آمدن عدد اول چند است؟

حل 4:

اعداد 31 تا 60 را نوشته و از روش غربال، اعداد اول را تعیین می‌کنیم و دور آن‌ها خط می‌کشیم:

مشاهده می‌شود که در این 30 عدد، 7 عدد اول هستند؛ پس حالت‌های مطلوب 7 و تعداد کل حالات ممکن 30 تاست. طبق رابطه، احتمال آمدن عدد اول در این چرخنده برابر است با:

\( \LARGE p=\frac {7}{30} \)

حالت‌های ممکن در یک پیشامد

دیدیم که در رابطه محاسبه احتمال ، مخرج کسر «تعداد همۀ حالت‌های ممکن» بود. برای محاسبه این عدد در حالتی که چند رویداد انجام می‌شود (مانند پرتاب یک سکه و چرخاندن یک گردونه شانس) روش‌هایی وجود دارد که عبارتند از:

1. نمودار درختی
2. جدول نظام‌دار

نمودار درختی

این روش، برای محاسبه حالات ممکن برای رخ دادن دو یا چند رویداد مناسب است. فرض کنید تعداد \( \large n \) رویداد رخ می‌دهد که رویداد اول 3 حالت، رویداد دوم 2 حالت، رویداد سوم 2 حالت دارند و همینطور تا رویداد \( \large n \) اُم ادامه پیدا می‌کند.

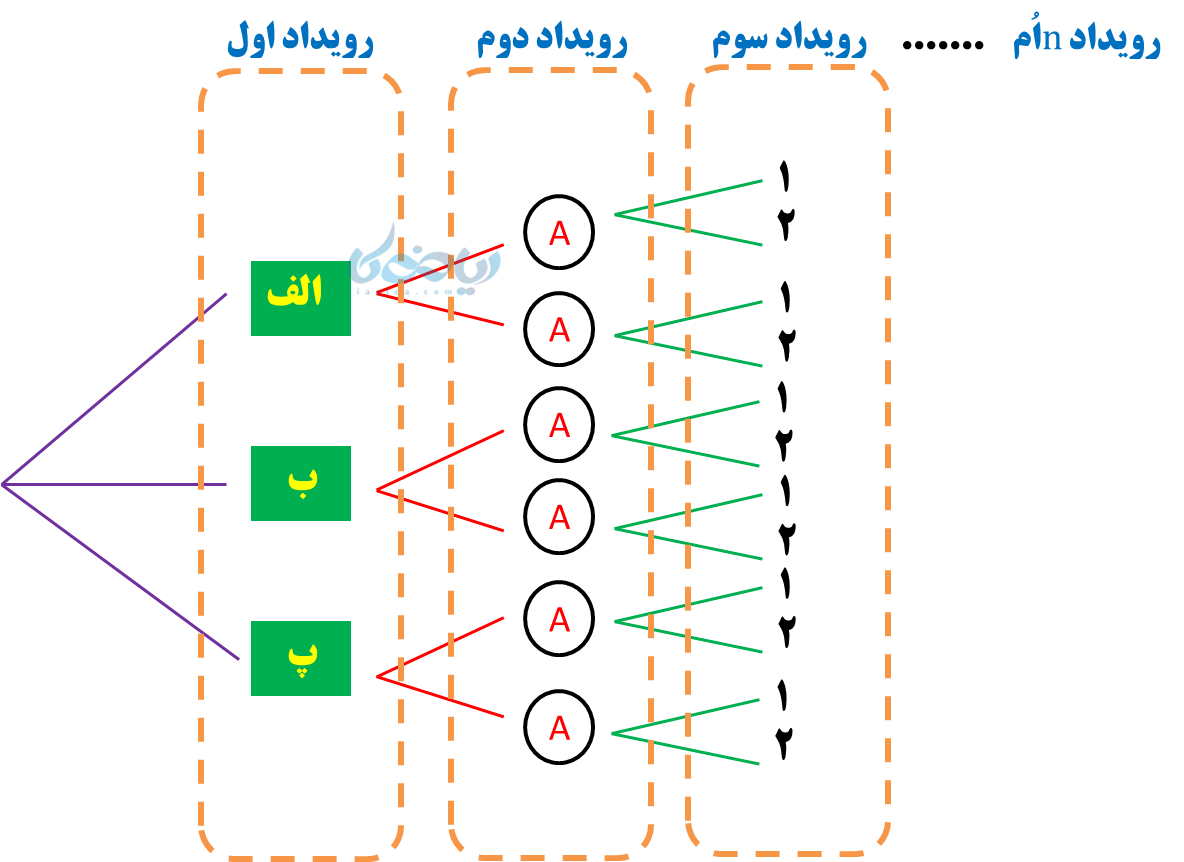
با این روش، می‌توان همه حالات ممکن و همچنین تعداد حالات مطلوب را پیدا کرد.

جدول نظام‌دار در احتمال هشتم

این روش، برای محاسبه حالات ممکن برای رخ دادن تنها دو رویداد مناسب است. حالت‌های رویداد اول را در ردیف افقی و حالت‌های رویداد دوم را در ستون عمودی می‌نویسیم.

نکته سرعتی: تعداد همه حالات ممکن، با ضرب کردن تعداد حالت‌های ممکن رویداد اول، تعداد حالت‌های ممکن رویداد دوم، تا تعداد حالت‌های ممکن رویداد \( \large n \) اُم بدست می‌آید.

مثال 5: یک تاس و یک سکه را با هم پرتاب می‌کنیم. مطلوب است:

الف) احتمال این که تاس عدد اول و سکه رو باشد.

ب) مشخص کردن 3 حالت هم‌شانس؛

حل 5:

دو رویداد داریم؛ بنابراین از هر دو روش نمودار درختی و جدول نظام‌‌دار می‌توانیم استفاده کنیم؛ برای یادگیری بیشتر مثال را از هر دو روش حل می‌کنیم:

نمودار درختی و جدول نظام‌‌دار این دو رویداد به شکل‌های ذیل هستند. مشاهده می‌شود مطابق هر دو روش، 12 حالت ممکن وجود دارد.

• نمودار درختی

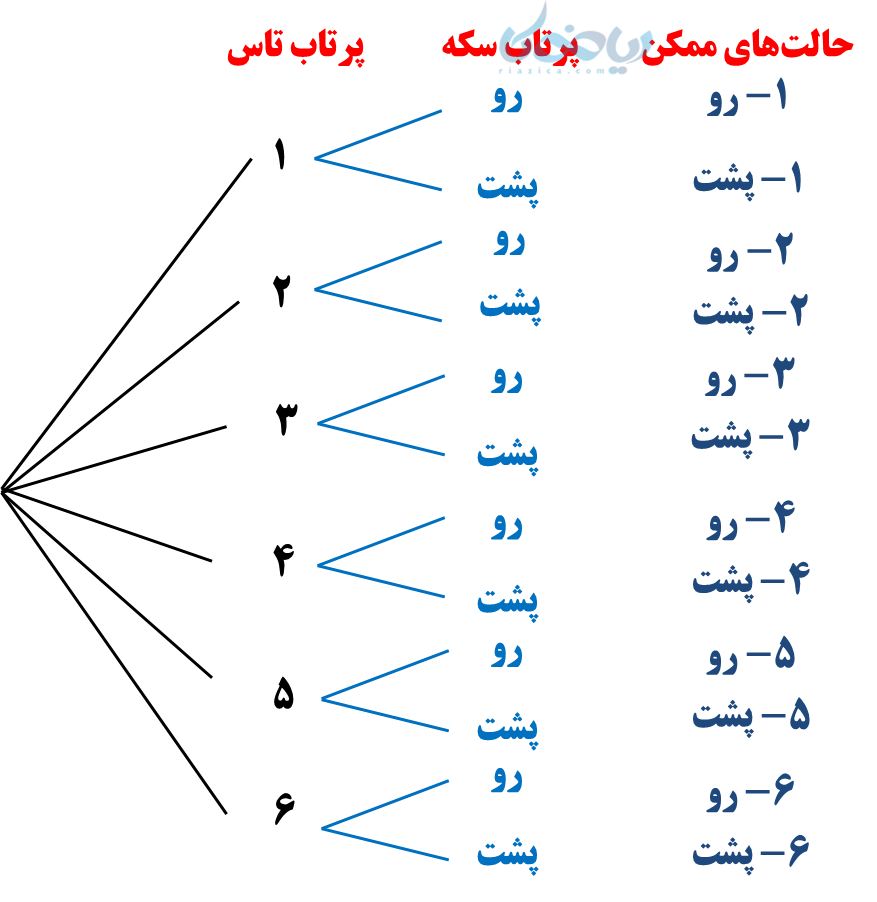
• جدول نظام‌دار

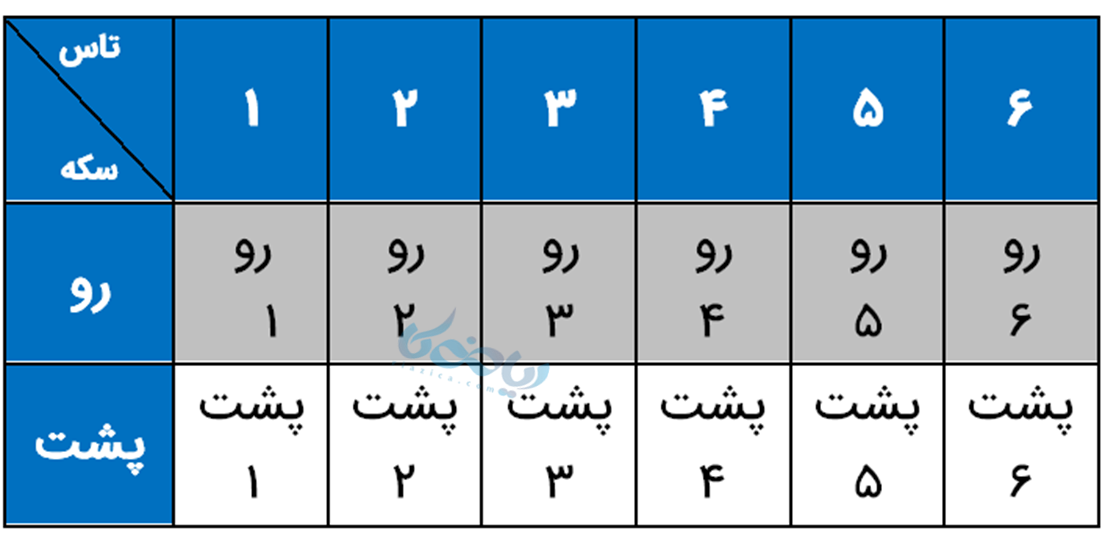
الف) اعداد اول بین 1 تا 6 عبارتند از: 2 ، 3 ، 5. پس این حالات شامل (2 رو، 3 رو، 5 رو) یعنی 3 حالت هستند و از آنجا که کل حالات 12 هستند احتمال آن برابر است با:

\( \LARGE p=\frac {3}{12} \)

\( \LARGE p=\frac {1}{4} \)

ب) احتمال این که تاس عدد فرد و سکه پشت بیاید (1 پشت، 3 پشت و 5 پشت). احتمال این که تاس عدد زوج و سکه رو بیاید (2 رو، 4 رو، 6 رو) و احتمال این که تاس عدد اول و سکه پشت بیاید (2 رو، 3 رو و 5 رو) هر سه برابر با \( \large \frac {3}{12} \) یا همان \( \large \frac {1}{4} \) بوده و از این رو این سه، حالت‌های هم‌شانس هستند.

فایل ویدیویی احتمال هشتم

برای تماشا کامل این ویدیو، دکمه خرید زیر این ویدیو را کلیک کنید:

زنگ آخر کلاس احتمال

در این درس‌نامه، به یادگیری رابطه احتمال رخ دادن یک پیشامد و حالت‌های هم‌شانس پرداختیم؛ همچنین با ذکر چند نکته بسیار مهم در مورد مجموع احتمال‌ها در یک مسأله، قدرت حل سؤال ما در این بخش بالا رفت. در ادامه برای مشخص کردن همۀ حالت‌های ممکن یک پیشامد، از دو روش نمودار درختی و جدول نظام‌‌دار استفاده کردیم.

در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.