آموزش ریاضی پایه دهم
تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
اسفند
میدونی تابع چند ضابطه ای (تابع قطعه ای) چه جوری رسم میشه؟ تشخیص دادنشو بلدی؟ ضابطه ها رو میتونی رسم کنی؟
برای جواب دادن به همه‌ی سوالاتت این نوشتار از دست نده.
تعریف اولیه از تابع چند ضابطه ای
تابع چند ضابطه ای یا قطعه ای، تابعی است که ضابطه یا همان نمایش جبری آن دارای معادله‌های مختلفی است. دو یا سه یا بیشتر. دامنهٔ هر معادله روبروی آن نوشته می‌شود. هر تابع می‌تواند قسمتی از یک تابع خطی، قسمتی سهمی، قسمتی تابع ثابت و حتی یک نقطه باشد.
توابع زیر نمونه‌هایی از توابع چند ضابطه ای هستند.
\( \LARGE f(x)= \begin{cases} x \hspace{4em} x \geq 0 \\ -x \hspace{3em} x<0 \end{cases} \)
\( \LARGE g(x)= \begin{cases} x^2 \hspace{4em} x \geq 0 \\ 3x-1 \hspace{1em} x<0 \end{cases} \)
\( \LARGE k(x)= \begin{cases} 1 \hspace{4em} x \geq 0 \\ -1 \hspace{3em} x<0 \end{cases} \)
\( \LARGE h(x) = \)
\( \LARGE \begin{cases} x-4 \hspace{4em} x > 1 \\ \frac{5}{2} \hspace{7em} x=1 \\ -x \hspace{4em} -4 \leq x<1 \end{cases} \)
با یک مثال تابع چند ضابطه ای را بهتر بفهمیم
مثال ۱: تابع چند ضابطه ای زیر را رسم کنید و سپس دامنه و برد آن را بنویسید.
\( \LARGE h(x) = \)
\( \LARGE \begin{cases} 2x-2 \hspace{4em} x > 2 \\ 5 \hspace{8em} x=2 \\ -2x \hspace{6em} x<2 \end{cases} \)
قطعه اول یک نیم خط
| 3 | 2 | x |
|---|---|---|
| 4 | 2 | y |
قطعه دوم یک نقطه
| 2 | x |
|---|---|
| 5 | y |
قطعه سوم نیز یک خط است
| -1 | 2 | x |
|---|---|---|
| 2 | -4 | y |
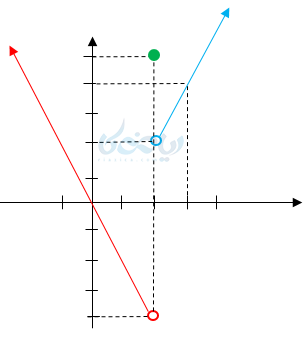
دقت کنید وقتی میخواهیم خط \( \Large ۲x-۲ \) را رسم کنیم. با توجه به اینکه دامنه \( \Large x>۲ \) است و ۲ جزء دامنه نیست، اما نقطه \( \Large (۲,۲) \) را پیدا می‌کنیم(به این نقطه، نقطه مرزی می‌گوییم).
نکته مهم این است که نقطه \( \Large (۲,۲) \) را در نمودار توخالی رسم می‌کنیم. پس حتماً باید نقطه مرزی دامنه را ابتدا پیدا کنیم. اگر جزء دامنه بود نقطه توپر و اگر نبود نقطه توخالی می‌گذاریم و نقاط بعدی را هم طبق دامنه پیدا می‌کنیم.
برای یک مثال دیگر از تابع چند ضابطه ای آماده‌اید؟
مثال ۲: نمودار تابع چند ضابطه ای \( \Large f \) داده شده است. ضابطه آن را به همراه دامنه و برد این تابع را بدست آورید.
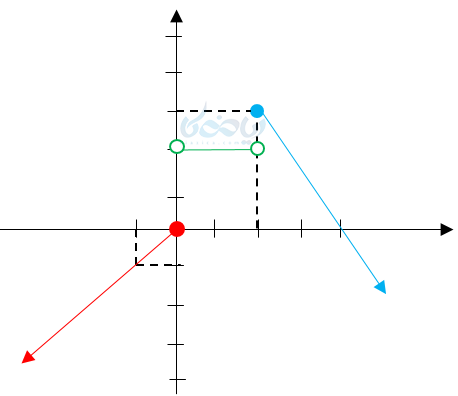
قطعه یک، یک تابع خطی است. برای نوشتن معادله آن به دو نقطه نیاز داریم. پس دو نقطه \( \Large (۴,۰),(۲,۳) \) را در نظربگیریم و شیب را پیدا کرده و معادله خط را می‌نویسیم:
\( \LARGE m=\frac{y_2-y_1}{x_2-x_1} \)
\( \LARGE m=\frac{3-0}{2-4} \)
\( \LARGE m=-\frac{3}{2} \)
\( \LARGE y=ax+b \)
\( \LARGE \rightarrow (4,0),a=-\frac{3}{2} \)
\( \LARGE 0=4\times (-\frac{3}{2})+b \)
\( \LARGE b=6 \)
\( \LARGE y=-\frac{3}{2}x+6 \)
اما دامنه‌اش \( \Large x \geq ۲ \) است.
قطعه دوم یک تابع ثابت است. پس \( \Large y=۲ \rightarrow ۰<x<۲ \)
قطعه سوم باز یک تابع خطی است و نیمساز ربع اول و سوم. پس معادله‌اش \( \Large y=x \) است با دامنه \( \Large x \leq ۰ \)
پس در کل داریم:
\( \LARGE h(x) = \)
\( \LARGE \begin{cases} -\frac{3}{2}x+6 \hspace{2em} x \geq 2 \\ 2 \hspace{8em} 0<x<2 \\ x \hspace{8em} x \leq 0 \end{cases} \)
آخر کلاس تابع چند ضابطه ای
در بحث آموزش تابع چند ضابطه ای ، این تابع مهم از ریاضی دهم را به ساده‌ترین و شیوا ترین حالت ممکن باهم یاد گرفتیم. همچنین مثالها و شکل‌های مختلفی از این نوع تابع دیدیم و مفهوم آن را باهم فرا گرفتیم. انواع دیگر تابع را می‌توانید در دیگر نوشتارهای آموزش ریاضی دهم بخوانید.
اگر هر سوالی از آموزش تابع چند ضابطه ای دارید، می‌توانید در پایین همین نوشتار در بخش دیدگاه‌ها سوال خود را مطرح کنید. ما در ریاضیکا به سوالات شما پاسخ می‌دهیم.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی دهم به شما پیشنهاد می‌دهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثال‌های متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!
تشكر
خوشحالیم که براتون مفید بوده
مثال از اگر نمودار تابع y=ax²+by+c باشد ضابطه تابع را بنویسید ؟
سلام و عرض ادب
سوال نامفهوم هستش.
دوباره بپرسید.
موفق باشید.
نیمساز ربع اول و سوم یعنی چی ربع دوم وچهارم یعنی چی؟
خط y=x نیمساز ربع اول و سوم است و خطی است که طول و عرض نقاط آن باهم برابر و از مبدا می‌گذرد و چون در هر ربع دو زاویه ۴۵ درجه می‌سازد به آن نیمساز ربع اول و سوم می‌گویند. نیمساز ربع دوم و چهارم نیز خط y=-x است.
من واااقعا ممنونم ازتون همه چی حل شد ??
خدا رو شکر
چگونه یک تابع یک ضابطه ای را به یک تابع دو ضابطه ای تبدیل کنیم ؟!
f(x)=[x]+[-x]۰
۰ رو بخاطر اینکه معادله درست نوشته شه گذاشتم ، وگرنه هیچ کار خاصی نمیکنه …
توابعی مثل توابع قدر مطلق یا توابع جزء صحیح را با توجه به تعریفشان در بازه‌های مختلف تعریف کرده و به چند ضابطه تبدیل می‌شوند. در این مثال اگر x عضو اعداد صحیح باشد f(x)=0 و اگر غیر صحیح باشد f(x)=-1 می‌شود. پس با توجه به دامنهٔ آن به یک تابع دو ضابطه‌ای تبدیل می‌شود.
سلام خسته نباشید
تشکر از مطالب مفیدتون
من یه سوال داشتم
چطور باید در تابع چند ضابطه ای که از ما خواسته شده ضابطه رو باتوجه به شکل بدست بیاریم
و شکل هم به هم وابسته است
ماجواب رو پیدا کنیم ؟؟؟
ضمن عرض سلام
شما لطف دارید خوشحالیم که براتون مفید بوده
نمودار را به چند قسمت تقسیم کنید. مثلا قسمتی که خط است، با استفاده از دو نقطه و شیب خط معادله‌اش را پیدا کنید. قسمتی که سهمی است نیز با توجه به راس و نقاط داده شده معادله‌اش را بنویسید. اگر به مثال‌های نوشته شده در این پست دقت کنید پاسخ خود را خواهید یافت.
چجور تشخیص بدیم تابع ضابطه ایه؟
اگر نمودار تابع داده شده باشد نمودارش از چند قسمت تشکیل شده مثلا هم خطی هم سهمی.
و اگر ضابطه داده باشد ضابطه آن چند قسمتی است یا مانند قدرمطلق با توجه به دامنه تعریفش میتوان برای آن چندضابطه تعریف کرد.
سلام و تشکر از مطالبتون
در ادامه چطور میشه یک به یک بودن و پوشا بودن توابع چند ضابطه ای رو مشخص کرد؟
ضمن عرض سلام و احترام
و تشکر بابت انرژی مثبتتون
در این توابع بهترین کار رسم نمودار و بررسی یک به یک و پوشا بودن از روی نمودار است.
سوال۱
تابع |y=|2x-1 را دو ضابطه ای کرده و رسم کنید. دامنه و برد این تابع را بنویسید.
سلام و عرض ادب
با توجه به ریشه ی داخل قدرمطلق، داخل قدرمطلق را یکبار بزرگتر مساوی ۱/۲ و یکبار کوچکتر از ۱/۲ قرار داده و آن دو خط را رسم کنید.
موفق باشید.
ممنون از شما
سلام
ممنون از انرژی که به ما دادید.
موفق باشید.
باید تو تابع چند ضابطه ای دقیقا پشت سر هم رسم بشن وهر نمودار نمی تونه روی نمودار دیگه باشه
با سلام وعرض احترام
چون تابع هست هیچ قسمت نمودار روی هم نمیفته ولی لزوما بهم وصل نیستند
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام خسته نباشید در مثال اول 2x-2 با دامنه ۲<x است بعد شما برای نقطه مرزی به جایxگذاشتین ۲ ۲ که جز جواب نیست نوشته 2<x تو برد های بعدیشم هم همه xها ۲چجوری حساب کردین قاعده خاصی داره ممنون از مطالب گرانبهایتان
اقا کسی نیست تو این سایت
با سلام وعرض ادب
بفرمایید
جناب اینو توضیح میدین
سلام و عرض خسته نباشید.
واقعا مطالبتان خیلی عالی و کامل بود. امیدوارم برای دوستان هم همین طور بوده باشه.
با سلام به شما دوست عزیز
خرسندیم که براتون مفید بوده معرف ما به دوستانتان باشید وتوصیه میشه پکیج دهم ما رو تهیه کنید
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام
تابع هایی مثل |X+1|+|x_2| و |X_|X چطر رسم میشن
با سلام و وقت به خیر اولی که نمودار گلدانی داره که با تعیبن علامت این عبارت به دست میاد کافیه ریشه های داخل قدرمطلق رو بدست بیارید وعبارت رو تعیین علامت کنید وبعد با توجه به جدول تعیین علامت قدرمطلقها رو برداشته وسه خط به دست اومده رورسم کنید شکلی شبیه گلدان میشه دومی هم مثل آخرین مثال پست رسم تابع جزصحیح که داخل سایت هست رسم میشه
سلام لطف کنید مبحث نوشتن معادله ازروی سهمی رو هم بزارید
تشکر
با سلام وعرض ادب
https://riazica.com/relationships-between-the-roots-of-the-quadratic-equation/
در این پست به این موضوع پرداخته ایم
تابع قطعه ای برابر با اشتراک یا اجتماع ضابطه است؟
با سلام وعرض ادب
اگه منظورتون دامنه تابع هست دامنه تابع چند ضابطه ای برابر با اجنماع تمام دامنه هاست
سلام و عرض ادب و احترام
من دبیر ریاضی هستم و برای آموزش بهتر تابع چندضابطه دنبال مطالب بیشتری بودم که مطالب بالا رو دیدم خیلی جامع و کامل به همه قسمتهای تابع چند ضابطه اشاره شده و مثالها و راه حل ها عالی
سپاس
سلام همکار محترم خوشحالیم که مطالب ما براتون مفید بوده چون حاصل سی سال تجربه هست خوشحالم یشیم سایت وپیج ما رو به دانش آموزانتون معرفی کنید
بابت مطلب مفیدتون تشکر
فقط یع سوال اینکه بدون رسم نمودا و فقط با داشتن ضابطه تابع چگونه بفهمیم در چه بازه ای در بالا یا پایین نیم ساز اول و در چه بازه در نیم ساز دوم و …. به همین ترتیب قرار دارند
من از یکی پرسیدم گفت شرط نیم ساز اول اینه که f(x)>x ولی آخه این واسه نیم ساز ربع دوم هم بر قراره که
با سلام وادب ضابطه تابع رو بیشتر از ایکس قرار بدید جواب نامعادله بازه مورد نظر هست
سلام ممنون از اموزش خوبتون
امکانش هست انتقال تابع علامت رو هم اموزش بدین?ممنونم
با سلام وادب
به زودی انشالله
سلام یه سوال داشتم وقتی یه محدوده و یک(f(x داده اند برای رسم نمودار قسمتی از نمودار خارج از محدوده چطور میشه؟ مثلا برای بازه [0،1]
(x=f(x. برای بازه[1,0-] چطور رسم میشه؟
با سلام وادب
کافیه اعداد ابتدا وانتهای بازه رو در تابع قرار بدید وبا توجه به اعداد بدست آمده نمودار تابع رو رسم کنید
در چه صورتی یک رابطه قطعه ای یک تابع هست ؟؟؟
با سلام
به ازای هر ایکس یک وای داشته باشیم در واقع شرایط تابع رو داشته باشه
ممنون،مختصر و مفید