آموزش ریاضی پایه یازدهم تجربی
روابط بین ریشه های معادله درجه دو ✖️➕ – مجموع و حاصل ضرب ریشه ها!
در این مبحث روابط بین ریشه های معادله درجه دو با هم یادمیگیریم. برایتان گاهی در معادلات درجه دوم برای ما مجموع یا حاصل ضرب ریشه ها اهمیت دارد یا اینکه مجموع یا حاصل ضرب ریشهها را داریم و معادله درجه دوم مدنظر ما میباشد. این موضوع اهمیت شناخت خاص مجموع و حاصل ضرب ریشههای معادله درجه دوم را برای ما آشکار میسازد که در این پست آموزشی به آن میپردازیم.
آموزش روابط بین ریشه های معادله درجه دو
ما بدون حل یک معادله درجه دوم قادریم مجموع و حاصل ضرب ریشه ها را بیابیم. معمولا مجموع در ریشه ها را با \(\Large s \) و حاصل ضرب آنها را با \(\Large P \) نمایش میدهند. حال اگر ریشههای معادله درجه دوم را \(\Large \alpha \) و \(\Large \beta \) در نظر بگیریم خواهیم داشت:
\(\LARGE s = \alpha + \beta \)
\(\LARGE p = \alpha \beta \)
نکته: در بعضی کتب ریشه ها را \(\Large x_1 \) و \(\Large x_2 \) نیز در نظر میگیرند.
معادله \(\Large ax^2+bx+c=0 \) را در نظر بگیرید میدانیم برای پیدا کردن ریشهها ابتدا باید \(\Large \Delta =b^2-4ac \) را بیابیم و اگر \(\Large \Delta > 0 \) باشد ریشهها به صورت زیر خواهد بود.
\(\LARGE \alpha = \frac{-b+\sqrt{\Delta}}{2a} \)
\(\LARGE \beta = \frac{-b-\sqrt{\Delta}}{2a} \)
پس داریم:
\(\LARGE s = \alpha + \beta \)
\(\LARGE = \frac{-b+\sqrt{\Delta}}{2a} + \frac{-b-\sqrt{\Delta}}{2a} \)
\(\LARGE = \frac{-2b}{2a} = \frac{-b}{a} \)
\(\LARGE p = \alpha \beta \)
\(\LARGE = (\frac{-b+\sqrt{\Delta}}{2a})(\frac{-b-\sqrt{\Delta}}{2a}) \)
\(\LARGE = \frac{b^2-\Delta}{4a^2}=\frac{b^2-b^2+4ac}{4a^2}=\frac{c}{a} \)
پس روابط بین ریشه های معادله درجه دو به صورت زیر خواهد بود:
- \(\LARGE s = \frac{-b}{a} \)
- \(\LARGE p =\frac{c}{a} \)

مثال 1: بدون حل معادله زیر مجموع و حاصل ضرب ریشه های (روابط بین ریشه های معادله درجه دو) آن را بیابید.
\(\LARGE -2x^2+x+5=0 \)
جواب 1:
اولا حتما این معادله دو ریشه دارد زیرا \(\Large a \) و \(\Large c \) مختلف العلامت هستند پس حتما خواهد \(\Large \Delta > 0 \) خواهد بود.
\(\LARGE s = \frac{-b}{a} = \frac{-1}{-2} = \frac{1}{2}\)
\(\LARGE p =\frac{c}{a} = \frac{5}{-2} = – \frac{5}{2} \)
چند نکته در مورد مجموع و حاصل ضرب ریشه ها
قدر مطلق تفاضل ریشهها
\(\LARGE \left| \alpha – \beta \right| = \frac{\sqrt{\Delta}}{\left| a \right|} \)
\(\LARGE \alpha ^ 2 + \beta ^ 2 = (\alpha + \beta)^2 – 2 \alpha \beta \)
\(\LARGE = s^2 – 2p \)
\(\LARGE \alpha ^ 3 + \beta ^ 3 \)
\(\LARGE = (\alpha + \beta)^3 – 3 \alpha \beta (\alpha + \beta) \)
\(\LARGE = s^3 – 3ps \)
\(\LARGE \alpha ^ 4 + \beta ^ 4 \)
\(\LARGE = (\alpha ^ 2 + \beta ^ 2)^2 – 2 \alpha ^ 2 \beta ^ 2 \)
\(\LARGE = (s^2-2p)^2 -2p^2 \)
\(\LARGE A^2 = (\sqrt{\alpha}+\sqrt{\beta})^2 \)
\(\LARGE = (\alpha+\beta)+ 2\sqrt{\alpha \beta} \)
\(\LARGE = s+2\sqrt{p} \)
\(\LARGE \sqrt{\alpha}+\sqrt{\beta} = \sqrt{s+2\sqrt{p} } \)
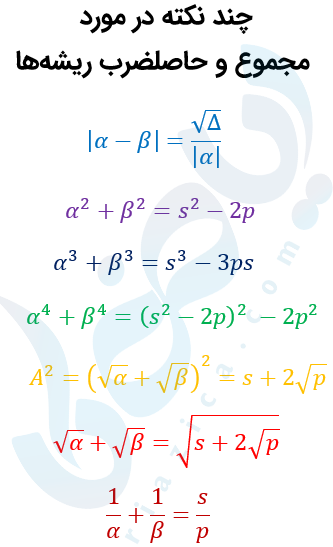
مثال 2: اگر \(\Large \alpha \) و \(\Large \beta \) ریشههای معادله \(\Large x^2-x-5=0 \) باشند حاصل \(\Large \frac{1}{\alpha}+ \frac{1}{\beta} \) را پیدا کنید.
جواب 2:
\(\LARGE \frac{1}{\alpha}+ \frac{1}{\beta} = \frac{\alpha + \beta }{\alpha \beta}=\frac{s}{p} \)
\(\LARGE \frac{-\frac{b}{a}}{\frac{c}{a}}= – \frac{b}{c} = – \frac{1}{5} \)
مثال 3: اگر \(\Large \alpha \) و \(\Large \beta \) ریشههای معادله \(\Large x^2-3x-2=0 \) باشند حاصل \(\Large \alpha ^ 4 + \beta ^ 4 \) را پیدا کنید.
جواب 3:
\(\LARGE s=-3,p=-2 \)
\(\LARGE \alpha ^ 4 + \beta ^ 4 = (s^2-2p)^2 -2p^2 \)
\(\LARGE \alpha ^ 4 + \beta ^ 4 = (9+4)^2 -8 \)
\(\LARGE \alpha ^ 4 + \beta ^ 4 =161 \)
مثال 4: اگر \(\Large \alpha \) و \(\Large \beta \) ریشههای معادله \(\Large x^2-7x+9=0 \) باشند حاصل \(\Large \sqrt{\alpha}+\sqrt{\beta} \) را پیدا کنید.
جواب 4:
\(\LARGE A^2 = (\sqrt{\alpha}+\sqrt{\beta})^2 \)
\(\LARGE A^2 = s+2\sqrt{p} \)
\(\LARGE = 7+2\sqrt{9} =13 \)
\(\LARGE A= \pm \sqrt{13} \)
\(\LARGE \sqrt{\alpha}+\sqrt{\beta} = +\sqrt{13} \)
چون \(\Large \sqrt{\alpha}+\sqrt{\beta} \) همواره مثبت است.
مثال 5: اگر \(\Large \alpha \) و \(\Large \beta \) ریشههای معادله \(\Large 5x^2-x-7=0 \) باشند حاصل \(\Large 5 \alpha ^ 2 + \beta + 3 \) را پیدا کنید.
جواب 5:
برای حل این مسئله یک راه پیدا کردن ریشهها و جایگذاری است که کمی طولانی میباشد ولی راه حل سادهتر این است که چون \(\Large \alpha \) ریشه معادله است پس در معادله صدق میکند یعنی داریم:
\(\LARGE 5 \alpha ^ 2 – \alpha -7=0 \)
\(\LARGE 5 \alpha ^ 2 = \alpha + 7 \)
پس داریم:
\(\LARGE 5 \alpha ^ 2 + \beta + 3 \)
\(\LARGE =(\alpha + 7) + \beta + 3 \)
\(\LARGE = \alpha + \beta + 10 = s + 10 \)
\(\LARGE = \frac{1}{5} + 10 = \frac{51}{5} \)
نکاتی در مورد ریشه های معادله درجه دو و روابط بین ریشه های معادله درجه دو
اگر یک معادله درجه دوم ریشه ها معکوس یکدیگر باشند یعنی حاصل ضرب ریشه ها یک خواهد شد پس داریم:
\(\LARGE p=1 \rightarrow \frac{c}{a}=1 \rightarrow c=a \)
یعنی اگر \(\Large a \) و \(\Large c \) مساوی باشند حتما ریشه ها معکوس یکدیگرند.
مثال 6: در معادله زیر \(\Large m \) را چنان بیابید که ریشههای این معادله معکوس یکدیگر باشند.
\(\LARGE 5x^2 – x + m=0 \)
جواب 6:
\(\LARGE 5x^2 – x + m=0 \)
\(\LARGE m=5 \)
اگر در یک معادله درحه دوم ریشهها قرینه هم باشند و داریم:
\(\LARGE s=\alpha + \beta = 0 \)
\(\LARGE s=-\frac{b}{a}=0 \rightarrow b=0 \)
پس اگر \(\Large b=0 \) باشد ریشهها قرینه یکدیگر خواهند بود.
مثال 7: در معادله زیر \(\Large m \) را چنان بیابید که ریشههای این معادله قرینه یکدیگر باشند.
\(\LARGE 7x^2 + (m-5)x -4=0 \)
جواب 7:
\(\LARGE 7x^2 + (m-5)x -4=0 \)
\(\LARGE m-5=0 \rightarrow m=5 \)
تشکیل معادله درجه دوم با استفاده از روابط بین ریشه های معادله درجه دو
فرض کنید \(\Large \alpha \) و \(\Large \beta \) ریشه های معادله درجه دوم باشند خواهیم داشت:
\(\LARGE (x-\alpha)(x-\beta)=0 \)
\(\LARGE x^2 – ( \alpha + \beta) + \alpha \beta =0 \)
\(\LARGE x^2 – sx + p=0 \)
یعنی اگر معادله درجه دومی که مجموع ریشههای آن \(\Large s \) و حاصل ضرب ریشه های \(\Large p \) باشد به صورت \(\Large x^2-sx+p=0 \) خواهد بود.
مثال 8: معادله درجه دومی بنویسید که ریشههای \(\Large 2-\sqrt{5} \) و \(\Large 2+\sqrt{5} \) باشد. (با روابط بین ریشه های معادله درجه دو حل شود.
جواب 8:
\(\LARGE s= \alpha + \beta \)
\(\LARGE s= 2+\sqrt{5} + 2-\sqrt{5} =4 \)
\(\LARGE p= \alpha \beta \)
\(\LARGE p= ( 2+\sqrt{5})( 2-\sqrt{5}) \)
\(\LARGE p= 4-5=-1 \)
\(\LARGE x^2-4x-1=0 \)
مثال 9: دو عدد حقیقی بیابید که مجموع آنها \(\Large \frac{1}{3} \) و حاصل ضرب آنها \(\Large – \frac{2}{3} \) باشد. (با روابط بین ریشه های معادله درجه دو حل شود.)
جواب 9:
\(\LARGE s= \frac{1}{3} \)
\(\LARGE p=- \frac{2}{3} \)
\(\LARGE x^2-\frac{1}{3}x- \frac{2}{3}=0 \)
حال معادله بالا را حل میکنیم جوابهای این معادله جوابهای مسئله میباشد برای راحتی ابتدا معادله را در ۳ ضرب میکنیم.
\(\LARGE 3x^2-x- 2=0 \)
\(\LARGE \Delta = 1 + 24 = 25 \)
\(\LARGE \alpha , \beta = \frac{1+\pm 5}{6} \)
\(\LARGE \alpha , \beta = 1 , -\frac{2}{3} \)
تشخیص علامت ریشههای معادله درجه ۲ بدون حل با استفاده از مجموع و حاصل ضرب ریشه ها
در یک معادله درجه دوم میتوان بدون به دست آوردن ریشهها علامت ریشههای را تشخیص داد و برای اینکار از مجموع ریشهها \(\Large s \) و حاصل ضرب ریشه ها \(\Large p \) کمک میگیریم.
- الف) معادله \(\Large \Delta > 0 \) دارای ۲ ریشه است.
اگر \(\Large p > 0 \) باشد. آن معادله دارای ۲ ریشه هم علامت است.
آنگاه دو حالت ممکن است.
اگر \(\Large s > 0 \) باشد. معادله دارای ۲ ریشه همعلامت و مثبت است.
اگر \(\Large s < 0 \) باشد. معادله دارای ۲ ریشه هم علامت و منفی است.
اگر \(\Large p < 0 \) باشد. آن معادله دارای ۲ ریشه مختلف العلامت است.
آنگاه دو حالت ممکن است.
اگر \(\Large s > 0 \) باشد. ریشه مثبت از مبدا دورتر و قدرمطلق بزرگتری دارد.
اگر \(\Large s > 0 \) باشد. ریشه منفی از مبدا دورتر و قدرمطلق بزرگتری دارد.
اگر \(\Large p = 0 \) باشد. حداقل یک ریشه صفر است.
آنگاه دو حالت ممکن است.
اگر \(\Large s > 0 \) باشد. معادله یک ریشه صفر و یک ریشه مثبت دارد.
اگر \(\Large s > 0 \) باشد. معادله یک ریشه صفر و یک ریشه منفی دارد.
- ب) اگر \(\Large \Delta = 0 \) معادله دارای یک ریشه مضاعف به صورت \(\Large x=-\frac{b}{2a} \) است که علامت آن با علامت \(\Large s \) مجموع ریشهها موافق است.
- ج) اگر \(\Large \Delta < 0 \) معادله فاقد ریشه است.
حل معادلات قابل تبدیل به معادله درجه دوم
گاهی میتوان معادلات درجات بالاتر مثل درجه چهارم یا ششم را به معادله درجه دوم تبدیل کرد و آنها را حل نمود.
مثال 10: معادله زیر را حل کنید.
\(\LARGE 3x^4 + 5x^2 – 1 = 0 \)
جواب 10:
کافیست با تغییر متغیر این معادله را به یک معادله درجه دوم تبدیل کنیم.
\(\LARGE x^2 = t , x^4 = t^2 \)
\(\LARGE 3t^2- 5t – 2 = 0 \)
\(\LARGE \Delta = 25+24=49 \)
\(\LARGE t_1 , t_2 = \frac{5\pm 7}{6} \)
\(\LARGE t_1 , t_2 = 2 , -\frac{1}{3} \)
\(\LARGE x^2 = 2 \rightarrow x=\pm \sqrt{2} \)
\(\LARGE x^2 =-\frac{1}{3} \)
چون \(\Large x^2 \) نمیتواند منفی باشد پس جواب \(\Large -\frac{1}{3} \) قابل قبول نیست. پس این معادله دو ریشه دارد.
نکته: یک معادله درجه چهار حداکثر میتواند ۴ ریشه داشته باشد.
مثال 11: معادله زیر را حل کنید.
\(\LARGE x^6-10x^3+9=0 \)
جواب 11:
کافیست با تغییر متغیر این معادله را به یک معادله درجه دوم تبدیل کنیم.
\(\LARGE x^3 = t ,x^6 = t^2 \)
\(\LARGE t^2- 10t +9 = 0 \)
\(\LARGE (t-1)(t-9)=0 \)
دیو ا\(\LARGE t=1 \rightarrow x^3 = 1 \rightarrow x=1 \)
\(\LARGE t=9 \rightarrow x^3 = 9 \rightarrow x=\sqrt[3] {9} \)
ویدیو از روابط بین ریشه های معادله درجه دو
در این ویدیو یک نمونه سوال از روابط بین ریشه های معادله درجه دو حل شده است
زنگ آخر روابط بین ریشه های معادله درجه دو
خوب رفقا باهم روابط بین ریشه های معادله درجه دو از ریاضی یازدهم تجربی را کامل یادگرفتیم. دوستان حتما عکسهای خلاصه را ذخیره کنید و مرورشون کنید. با حل کردن چندتا مثال به راحتی آب خوردن میتونید رو این بحث مسلط بشید.
هر سوالی از این مبحث داشتید کافیه برامون در قسمت دیدگاه بنویسید. کارشناسان ریاضیکا قطعا بهتون پاسخ میدهند.





سلام ..سایت خیلی عالی هست و تدریس بسیار خوب هست..لطفا اگ میشه نمونه سوال یازدهم تدریس هم بزارید ممنون میشم??
سلام و عرض ادب
ممنون از توجهی که داشتید. حتما در آینده داخل سایت قرار می دهیم.
موفق باشید.
سلام ببخشید اگه دلتا با یکی از ریشه ها برابر بشه چه اتفاقی میفته؟
سلام و عرض ادب
اتفاق رخ نمیدهد.
موفق باشید.
چرا میگید این اتفاق نمیفته؟؟؟
یا سلام
نمیگوییم اتفاق خاصی نمی افتد قط ریشه دیگر دو برابر این ریشه خواعد بود
اصل بده
پس چرا این تست جواب داره؟
اگر یکی از ریشه های معادله ax²+bx+c برابر با دلتای معادله باشد بیشترین مقدار ab چقدر است؟
۱)۱ ۲)½ ۳)¼ ۴)⅛
سلام دوست عزیز گزینه الف درست است یعنی ریشه دیگر دو برابر آن خواهد بود
جواب گزینه ۴ هست
سلام سایت عالی هست
فقط من یک مشکل دارم
وقتی در سوالات مطرح میشود که دو معادله داده شده(در معادله بجای ضرایب مجهول گذاشته شده) حداقل یک ریشه یکسان دارند ضرایب مجهول را بیابید
اینجا باید چه کار کنیم؟
با سلام واحترام
به این معادلات پارامتری می گویند چون گفته ریشه یکسان یعنی دلتا صفر باشد پس دلتا را پیدا میکنید که خودش یک عبارت جبری بر اساس ضرایب خواهد بود سپس ان را برابر صفر گذاشته ومقدار ضریب را به دست می اورید
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
خیلی ممنون و متشکر
چشم حتما
با سلام وعرض ادب
ممنون از نظر لطف شما
یک یکی حرف نداری
با سلام وعرض ادب
ممنون از نظر لطف شما
سلام
یه اشتباه کوچیک هستش. برای اینکه ریشه ها معکوس باشند c و a باید برابر باشند نه قرینه c/a=1 => c=a
با سلام دوست گرامی
ممنون از دقت نظر شما اصلاح میشه
حرف نداری.
با سلام واحترام
ممنون از نظر لطف شما کابران ما هم حرف ندارن
سلام ممنون از سایت خوبتون، من سال دهم هستم و این فرمول هارو تاحالا ندیده بودم. برای حسابان یازدهم هستن؟ یا مسائل اضافه بر کتب درسی برای محاسبه سریعتر هستن که در مدارس خاص آموزش داده میشن؟ چون من مدرسه معمولی هستم. خیلی ممنون میشم پاسخ بدین
با سلام وعرض ادب
ممنون از شما دوست عزیز این مطلب مربوط به پایه یازدهم میباشد
سلام وقتتون بخیر میخواستم بدونم از کجا باید نمونه سوال این درس رو پیدا کنم چون من امتحان دارم .ممنون میشم اگر جواب بدهید.
این 5-=m درسته؟یا m باید مثبت 5 باشه؟
همون مثال 6 شماست
مثال 6: در معادله زیر m را چنان بیابید که ریشههای این معادله معکوس یکدیگر باشند.
5×2–x+m=0
m=−5
با سلام وعرض ادب
بله مثبت پنج درسته اصلاح شد
سلام وقتتون بخیر میخواستم بدونم از کجا باید نمونه سوال این درس رو پیدا کنم چون من امتحان دارم .ممنون میشم اگر جواب بدهید.
با سلام وعرض ادب
متاسفانه در اینمورد نمونه سوال نداریم
عالیسن
با سلام وعرض ادب
ممنون دوست عزیز
فکر کنم جواب رادیکاله آلفا به اضافه بتا اشتباه چون شما A^2حساب کردین
باید در آخر از طرفین جذر بگیرید
سلام دوست عزیز به درسنامه دقت کنید متوجه میشید درسته
سلام میشه ی نمونه بگید ک حاصلضرب ریشه ها یک بشه
با سلام
دوست عزیز اگه پست رو خوب بخونید گفبیم اگه a,cمساوی باشند حاصلضرب ریشه ها یک میشود
سلام ببخشید اگر بهمون معادله با ضریب ۴ بده و ما هم تغییر متغیر انجام بدیم ولی ار رو همون معادله از ما S و P بخواد باید چیکار کنیم؟
با سلام وادب
اس و پی برای همون معادله درجه دومی هست که با تغییر متغیر بدست آوردید
سلام این معادله چطور حل میشه
معادله درجه دومی بنویسید که ریشه های آن ۴و۲_ باشد
ممنونم
با سلام
پست رو بخونید به جواب کیرسید
ثابت کردن قدر مطلق یا ریشه الفا منها بتا برابر با رادیکال دلتا به روی قدر مطلق a رو میخواستم
با سلام اینجا امکانش نیست
سلام میخواستم بدونم p با c برابر است یعنی ضرب ریشه ها با محل برخورد با محور ایگرگ ها برابره
با سلام وادب
خیر فقط c محل برخورد نمودار با محور عرضها رونشون میده
استاد وقتی یه معادله میده سوال و 4 تا معادله تو گزینه ها میده و میگه ریشه های کدوم معادله از معکوس ریشه های معادله فوق یک واحد کمتر باشد اینجا باید چیکار کنیم؟
بسیاررعالی و کامل و جامع.
با سلام دوست عزیز
سپاس از نظر لطف شما
یک رابطه بین ریشه سوم الفا به اضافه ریشه سوم بتا چی میشه ممنون میشم بگید
سلام دوست عزیز
اگه پست رو دقیق بخونید جوابتون رو پیدا میکنید
ببخشید در روابط بین ریشه ها اگر a b ریشه ها باشن: 6b+aبه توان ۲ چطور حل میشه؟ بر حسب s p
ببخشید ازکجا بفهمیم pوsمقبت یا منفی هستن از روی شکل
تابع؟
با سلام
وقتی از روی ضرایب بدستشون بیارید علامتشون مشخص میشه پست رو درست بخونید یه باردیگه به جوابتون میرسید
سلام مثال دو اگه مخرج زیر رادیکال باشه راه حلش چطوره
با سلام دوست عزیز
ابتدا مخرجها رو گویا کنید وبعد مخرج مشترک بگیرید واز روابطی که قبل این سوال اومده استفاده کنید
سلام وقتی معادله ریشه مضاعف داره هم مجموع ریشه ها با s تعریف میشه ؟ یا s وp برای دلتا بزرگتر از صفر هست؟
با سلام
وقتی ریشه مضاعفه یعنی ریشه ها تکراری ومثل هم هستن پس مجموعشون میشه دوبرابر یه ریشه
sوp هر جا که ریشه باشه هست خوب وقتی دلتا منفی ریشه ای نیست که مجموع یا حاصلضرب داشته باشه
سلام. نکات این پست رو یاداشت کنیم مشکلی پیش نمیاد؟ از لحاظ مادی و معنوی درسته؟
سلام دوست عزیز
برا استفاده شخصی یا آموزش به دانش اموزان مشکلی نیست اما کپی واستفاده در سایتهای دیگر مجاز نیست
واقعا برای مرور عالیه دم شما گرم. خدا قوت
سلام و وقت بخیر
ممنونیم از شما و خوشحالیم که براتون مفید بوده
موفق و پیروز باشید
سلام ممنون از مطالب کاملتون.ببخشید برای نکته رادیکال S به اضافه دو رادیکال P چطوری اثبات میشه که برابر میشه با رادیکال آلفا به اضافه رادیکال بتا
با سلام
با توان رسانی و طرف به جواب میرسید
سلام یه قدر مطلقی هم کاشکی حل میکردید
برای حل آلفا به توان ۲ در بتا + آلفا در بتا به توان ۲
از چه فرمولی باید استفاده بشه ؟
با سلام اگه متن رو بخونید به جوابتون میرسید
عالی بود
تشخیص علامت ریشههای معادله درجه ۲ بدون حل با استفاده از مجموع و حاصل ضرب ریشه ها
این بخش را اشتباه نوشتید.
سلام دوست عزیز
کجاش اشتباه هست؟
درود اگر دو ریشه قرینه و معکوس هم باشند باید P= _1 باشد . چرا نیازی به دلتای مثبت نیست ؟
عالی بود خیلی ممنون خیر ببینین
تشکر از شما
سلام دوست عزیز ممنون از نگاه شما
ممنون خیلی کاربردی بود