آموزش ریاضی پایه یازدهم تجربی، آموزش هندسه دهم ریاضی
روابط طولی در مثلث قائم الزاویه ، قضیه تالس و تشابه مثلث ها 📐⏩ : نتیجه یک همکاری خوب!
با استفاده از تشابه مثلثها و قضیه تالس میتوان در یک مثلث قائم الزاویه روابط زیبایی بین ضلعها، ارتفاعِ وارد بر وتر و پارهخطهای به وجود آمده پیدا کرد. این روابط به روابط طولی در مثلث قائم الزاویه معروف هستند. با استفاده از این روابط طولی میتوان با داشتن بعضی از اجزاء مثلث قائم الزاویه بقیه اجزاء را پیدا کرد.
اثبات روابط طولی در مثلث قائم الزاویه به کمک قضیه تالس
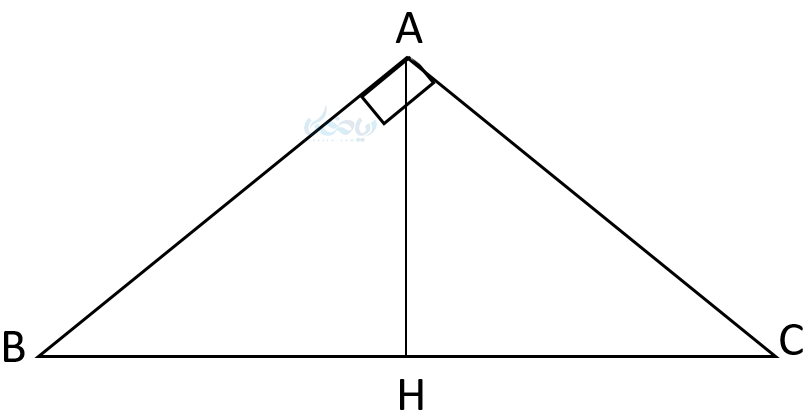
فرض کنید مثلث ABC یک مثلث قائم الزاویه و AH ارتفاع وارد بر وتر آن باشد.
اولاً مثلث ABC و AHC با هم متشابهاند. زیرا:
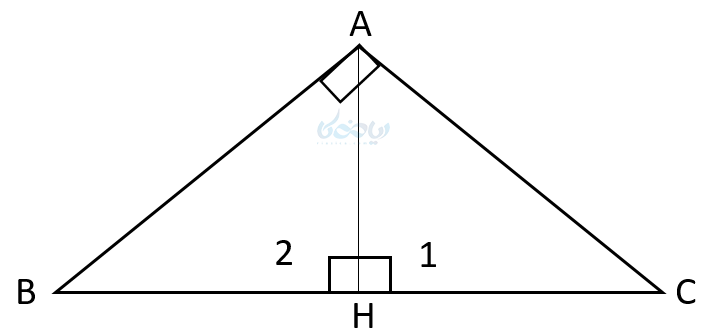
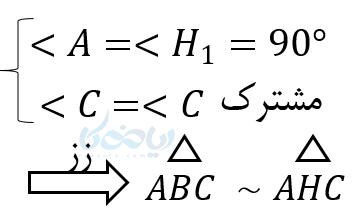
از طرف دیگر مثلث ABC و ABH نیز با هم متشابهاند. زیرا:
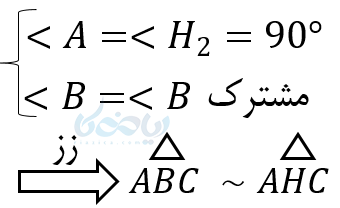
چون دو مثلث AHB و AHC با مثلث ABC متشابهاند، پس این دو مثلث با یکدیگر نیز متشابهاند. به هر حال از تشابه مثلثها روابط طولی زیر را نتیجه میگیریم:
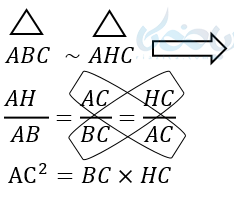
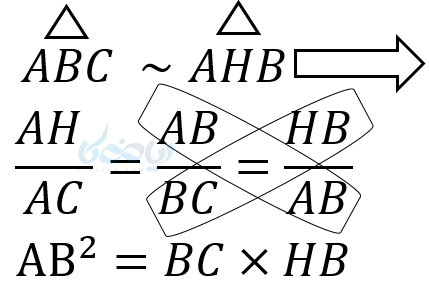
این دو رابطه به ما میگن هر ضلع زاویه قائمه به توان دو برابر است با تیکه طرف خودش ضربدر وتر
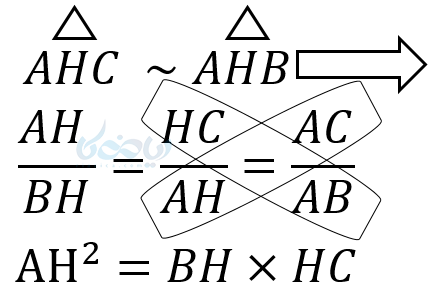
اثبات قضیه فیثاغورس با استفاده از روابط طولی مثلث قائم الزاویه
مثال ۱: با استفاده از روابط طولی در مثلث قائم الزاویه قضیه فیثاغورس را اثبات کنید؟
حل ۱: با استفاده از آموزش قضیه تالس و طبق روابط طولی در مثلث ABC داریم.
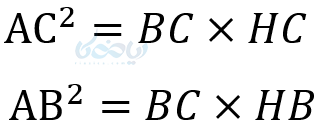
جمع طرفین:
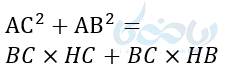
از \( \LARGE BC \) فاکتور میگیریم:
![]()
![]()
در نتیجه به رابطه فیثاغورس میرسیم:
![]()
یکی از روابط طولی در مثلث قائم الزاویه به صورت زیر اثبات میشود. اگر بخواهیم مساحت مثلث قائم الزاویه ABC را به دو طریق محاسبه کنیم خواهیم داشت:
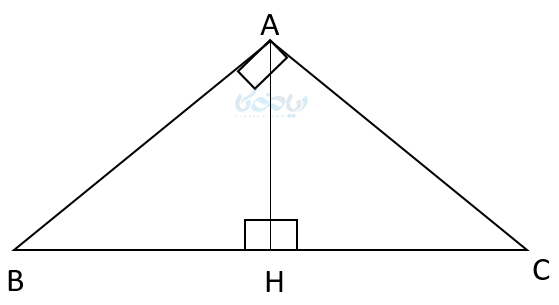
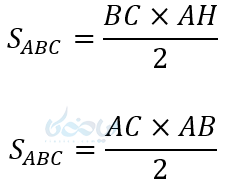
دو رابطه مساحتها را برابر قرار میدهیم:
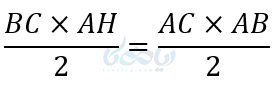
![]()
به زبان ساده حاصلضرب دو ضلع زاویه قائمه برابر است با ارتفاع وارد بر وتر ضربدر وتر
پس پنج رابطه طولی مهم در مثلث قائم الزاویه ABC داریم:
پنج رابطه طولی در مثلث قائم الزاویه
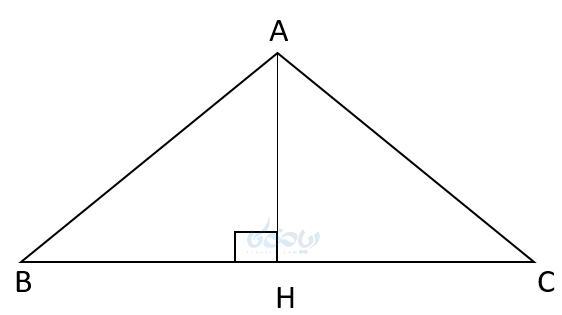
- \( \LARGE AC^2 = BC \times HC \)
- \( \LARGE AB^2 = BC \times HB \)
- \( \LARGE AH^2 = BH \times HC \)
- \( \LARGE BC \times AH \)
- \( \LARGE = AC \times AB \)
- \( \LARGE AC^2 + AB^2 = BC^2 \)
مثال از روابط طولی مثلث قائم الزاویه
مثال ۱۰: در شکل زیر BH = 5 , HC = 3 است AC , AB را بدست آورید؟
حل ۱۰: با استفاده از آموزش قضیه تالس و طبق روابط طولی در مثلث ABC داریم.
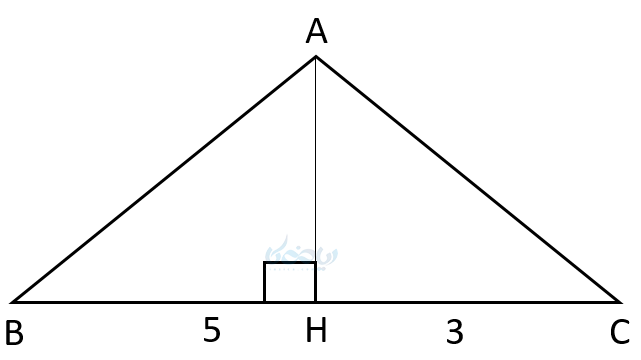
\( \LARGE AC^2 = BC \times HC \)
\( \LARGE AC^2 = 8 \times 3 = 24 \)
\( \LARGE AC = \sqrt24 = 2\sqrt6 \)
\( \LARGE AB^2 = BC \times HB \)
\( \LARGE AB^2 = 8 \times 5 = 40 \)
\( \LARGE AB = \sqrt40 = 2\sqrt10 \)
مثال ۲: در شکل زیر AH = 5 , BH = 7 است AC , AB را بدست آورید؟
مثال ۲: با استفاده از آموزش قضیه تالس و طبق روابط طولی در مثلث ABC داریم.
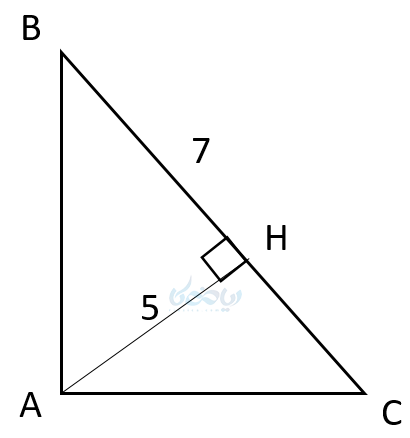
\( \LARGE AH^2 = BH \times HC \)
\( \LARGE 25 = 7 \times HC \)
\( \LARGE HC = \frac{25}{7} \)
\( \LARGE BC = BH + HC \)
\( \LARGE BC = 7 + \frac{25}{7} = \frac{74}{7} \)
\( \LARGE AB^2 = BC \times HB \)
\( \LARGE AB^2 = \frac{74}{7} \times 7 \)
\( \LARGE AB = \sqrt74 \)
\( \LARGE AC^2 = BC \times HC \)
\( \LARGE AC^2 = \frac{74}{7} \times \frac{25}{7} \)
\( \LARGE AC = \frac{1850}{49} \)
قبل از خوندن این پست درسنامه قضیه تالس و تشابه مثلث ها را مطالعه کنید.
کلام آخر
در این نوشتار که از مباحث جذاب در آموزش ریاضی یازدهم تجربی و آموزش هندسه دهم بود، روابط همراه با مثالها و اشکال گوناگون برای فهم بهتر شما عزیزان آورده شد. در طول این آموزش تمامی این روابط را با هم بررسی کردیم و یاد گرفتیم.
شما میتوانید در بخش دیدگاهها تمامی سوالهایتان را از این نوشتار با ما در میان بگذارید. کارشناسان ریاضیکا به سرعت به سوالات شما پاسخ خواهند داد.




خیلی عالی بود من بهتر از فیلما متوجه شدم
سلام و عرض ادب
خیلی خوشحالیم که براتون مفید بوده است.
موفق باشید.
خیلی عالی توضیح دادید
خیلی ممنون خسته نباشید??
با سلام وادب
خدا رو شکر مفید بوده
عالی بود به سادگیها گرفتم مطلبی که همیشه ازش ترس داشتم
با سلام دوست عزیز
سپاس از نظر لطف شما واقعا ریاضی اگه فهمیده بشه لذت بخش ترین درس دنیاست
خیلی خوب واقعا کمکم کرد
خدا رو شکر
خیلی ممنون
با سلام
ممنون از نگاه شما
سلام
وقت همگی بخیر
در تصویر پنج از ابتدای مقاله (استفاده از تشابه برای دو مثلث کوچک تر ) نسبت ها درست هستش اما کار مستطیلی (ضربدری) به اشتباه دو نسبت دیگر رو مشخص کرده
منون از دقتنظر شما اصلاح میشه