رسم نمودار تابع قدر مطلق به زبان شکل‌ها 📒📉

در این نوشتار از مجموعه آموزش‌ ریاضی دهم در مورد رسم نمودار تابع قدر مطلق باهم گفت و گو خواهیم کرد. اگر بخواهیم تعریف دقیقی از تابع قدر مطلق به شما ارائه دهیم باید بگوییم:

تابعی که هر مقدار از دامنه را به قدر مطلق آن در برد نظیر می‌کند تابع قدر مطلق می‌نامند.

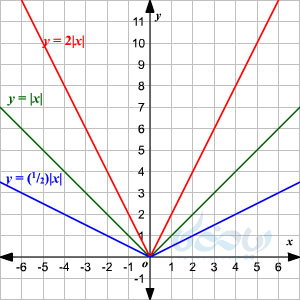
ضابطهٔ آن به صورت \( \Large f(x)=\left| x \right| \) یا \( \Large y=\left| x \right| \) می‌نویسند. دامنهٔ این تابع \( \Large \mathbb{R} \) است اما برد آن \( \Large [0,+\infty) \) خواهد بود.

---

---

نمودار تابع قدر مطلق

طبق تعریف قدر مطلق داریم:

\( \LARGE f(x)=\left| x \right|= \begin{cases} x \hspace{2em} x \geq 0 \\ -x \hspace{1em} x<0  \end{cases} \)

به طور کلی مطابق عبارت ریاضی بالا دو حالت را می‌توان بیان کرد:

• اگربه جای \( \Large x \) مقدار مثبت یا صفر قرار بگیرد مقدار خود عدد از داخل قدر مطلق بیرون می‌آید.
• اگر عدد منفی قرار بگیرد قرینه‌اش بیرون می‌آید. مانند \( \Large y=\left| -2 \right| = -(-2)=2 \) یا \( \Large y=\left| 2 \right| =2 \)

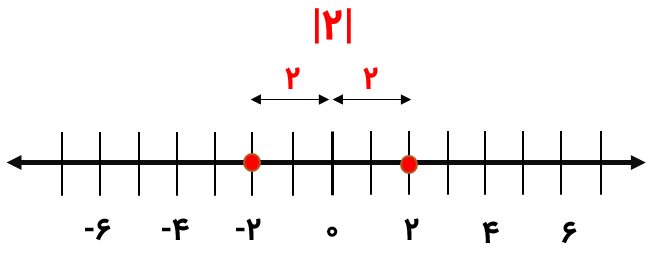
پس در واقع ما یک تابع دوضابطه‌ای یا قطعه‌ای داریم که از دو خط با دامنه‌های مختلف تشکیل شده اگر این دو خط را رسم کنیم. داریم:

\( \LARGE f(x)=\left| x \right|= \begin{cases} x \hspace{2em} x \geq 0 \\ -x \hspace{1em} x<0  \end{cases} \)

1	۰	x
1	۰	y

-1	۰	x
1	۰	y

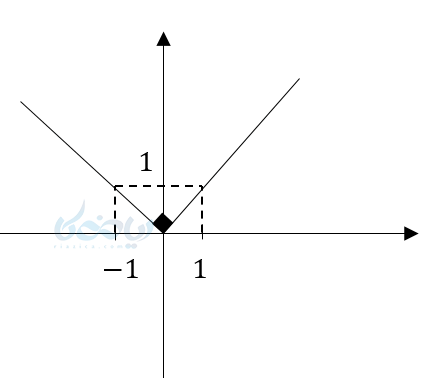
که یک هفت با راس روی مبدا را تشکیل می‌دهد (با زاویه 90)

حال که نمودار تابع قدر مطلق را شناختیم می‌توانیم با روش نقطه یابی سریع‌تر نمودار را رسم کنیم کافیست راس و یک واحد قبل و بعد راس را در یک جدول پیداکرده و نمودار تابع را رسم کنیم.

مثال ۱ از رسم نمودار تابع قدر مطلق: نمودار تابع \( \Large y=- \left| x \right| \) را رسم کنید؟

حل ۱: برای پیداکردن راس سهمی کافیست ریشه داخل قدر مطلق را پیدا کنیم (طول راس)

و با جایگذاری آن \( \Large y \) راس را پیدا کنیم در این مثال \( \Large x=0 \) ریشه داخل قدر مطلق و در واقع طول راس است و \( \Large y=0 \) ، نیز عرض راس پس راس \( \Large S:(0,0) \) است حال داخل جدول نوشته و یک واحد قبل و بعد طول راس را می‌نویسیم.

1	۰	-1	x
-1	۰	-1	y

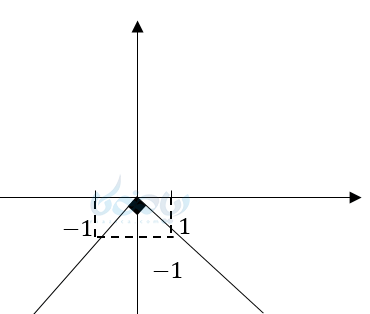
این نمودار قرینه نمودار \( \Large y=\left| x \right| \) است و شبیه یک هشت می‌شود پس اگر ضریب قدر مطلق مثبت باشد نمودار \( \Large \bigvee \) و اگر منفی باشد \( \Large \bigwedge \) می‌شود.

به طور کلی نمودار تابع  \( \Large f(x) \) و \( \Large -f(x) \) نسبت به محور طول‌ها قرینه یکدیگرند.

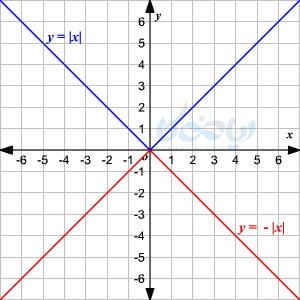
مثال ۲ از رسم نمودار تابع قدر مطلق: نمودار \( \Large y=\left| x-2 \right| \) را رسم کنید؟

حل ۲: ریشه داخل قدر مطلق (\( \Large x \) راس)

\( \LARGE x=2 \rightarrow y=0 \)

راس \( \LARGE S:(2,0) \)

3	2	1	x
1	۰	1	y

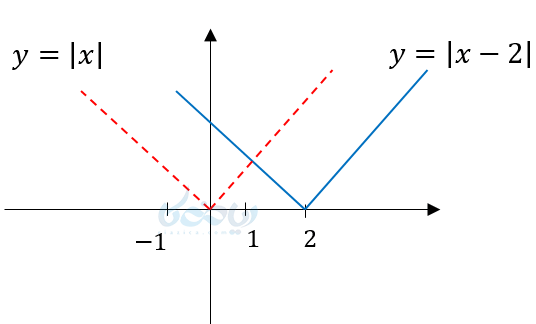
اگر دقت کنید \( \Large x \) داخل قدر مطلق منهای دو شده ولی نمودار نسبت به نمودار \( \Large y=\left| x \right| \) دو واحد به سمت راست منتقل شده ما به این نوع انتقال، انتقال درونی می‌گوییم و به اصطلاح تابع در این مواقع لجباز است.

یک روش دیگر رسم نمودار روش انتقال است به صورتی که ابتدا نمودار \( \Large f(x) \) که ما به آن نمودار مادر یا اصلی می‌گوییم را رسم کرده سپس نمودار تابع جدید را انتقال می‌دهیم.

مثال ۳ از رسم نمودار تابع قدر مطلق: نمودار \( \Large y=\left| x+3 \right| \) را رسم کنید؟

حل ۳: ریشه داخل قدر مطلق (\( \Large x \) راس)

\( \LARGE x=-3 \rightarrow y=0 \)

راس \( \LARGE S:(-3,0) \)

-2	-3	-4	x
1	۰	1	y

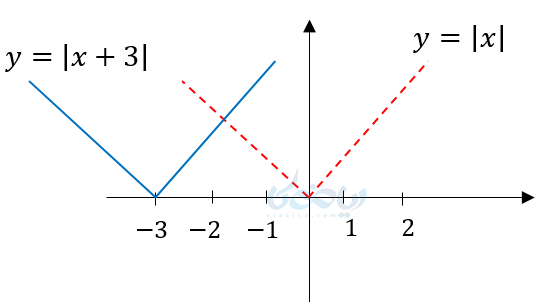
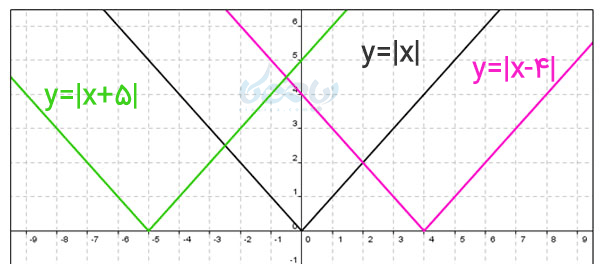
اگر دقت کنید \( \Large x \) داخل قدر مطلق بعلاوه 3 شده است اما نمودار سه واحد به سمت چپ منتقل شده است پس انتقال درونی به سمت چپ و یا راست است و تابع لجباز است به طور کلی:

با داشتن نمودار تابع \( \Large f(x) \)  می‌توان نمودار تابع \( \Large f(x+h) \)  را به روش انتقال رسم کرد.

اگر \( \Large h>0 \) باشد  \( \Large h \) واحد به سمت چپ و اگر \( \Large h<0 \)  باشد \( \Large h \)  واحد به سمت راست نمودار را منتقل می‌کنیم.

مثال ۴ از رسم نمودار تابع قدر مطلق: نمودار \( \Large y=\left| x \right| +2 \) را رسم کنید؟

حل ۴: ریشه داخل قدر مطلق (\( \Large x \) راس)

\( \LARGE x=0 \rightarrow y=2 \)

راس \( \LARGE S:(0,2) \)

1	۰	-1	x
3	2	3	y

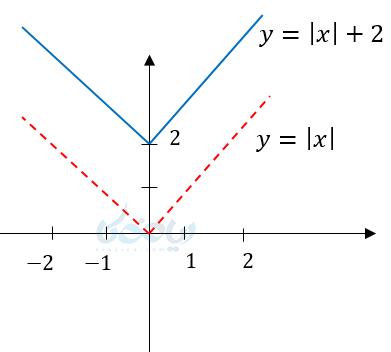
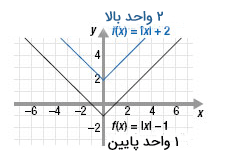
در اینجا قدر مطلق با عدد دو جمع شده است و راس سهمی 2 واحد به سمت بالا انتقال پیدا کرده است پس انتقال از نوع بیرونی است و تابع از اینکار تبعیت می‌کند یعنی در موقع جمع به بالا و در موقع تفریق به پایین انتقال می‌یابد.

مثال ۵ از رسم نمودار تابع قدر مطلق: نمودار \( \Large y=\left| x \right| -2 \) را رسم کنید؟

حل ۵: ریشه داخل قدر مطلق (\( \Large x \) راس)

\( \LARGE x=0 \rightarrow y=-2 \)

راس \( \LARGE S:(0,-2) \)

1	۰	-1	x
-1	-2	-1	y

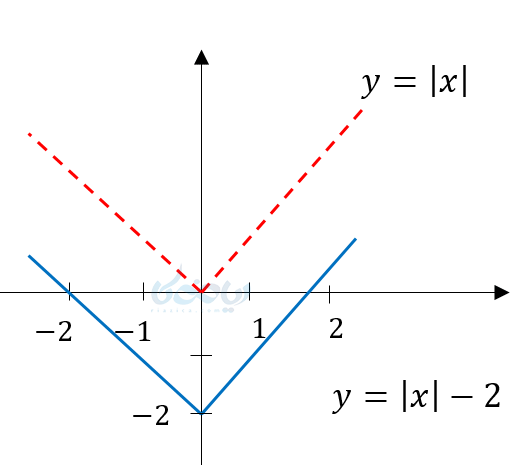
قدر مطلق منهای 2 شده پس نمودار دو واحد به پایین منتقل شد.

با داشتن نمودار \( \Large f(x) \) تابع می‌توان نمودار تابع \( \Large f(x)+k \)  را به روش انتقال رسم کرد.

اگر \( \Large k>0 \)  باشد \( \Large k \) واحد به سمت بالا و اگر \( \Large k<0 \)  باشد \( \Large k \) واحد به سمت پایین نمودار را منتقل می‌کنیم.

مثال ۶ از رسم نمودار تابع قدر مطلق: نمودار \( \Large y=\left| x-2 \right| +1 \) را رسم کنید؟

حل ۶: ریشه داخل قدر مطلق (\( \Large x \) راس)

\( \LARGE x=2 \rightarrow y=1 \)

راس \( \LARGE S:(2,1) \)

3	2	1	x
2	1	2	y

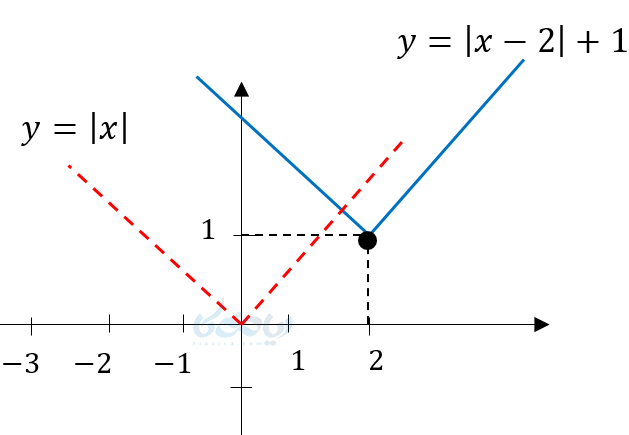
در این مثال تابع دو واحد به سمت راست و یک واحد به سمت بالا منتقل شده است. یعنی هم انتقال درونی و هم بیرونی داریم.

نکته رسم نمودار تابع قدر مطلق : در رسم نمودار به روش انتقال احتیاج به جدول نیست. ابتدا نمودار در \( \Large y=f(x)\) را رسم کرده و سپس آن را طبق تابع جدید انتقال می‌دهیم.

نکته رسم نمودار تابع قدر مطلق : رسم نمودار به روش نقطه‌یابی دقیق‌تر و بهتر از روش انتقال است ولی در روش انتقال سریع‌تر می‌توان نمودار را رسم کرد و در سریع جواب دادن به تست ها مورد استفاده قرار می‌گیرد.

 

مثال ۷ از رسم نمودار تابع قدر مطلق: تابع \( \Large y=-\left| x-3 \right| +2 \) را رسم کنید؟

حل ۷: در این مثال چون پشت قدر مطلق منفی داریم پس اگر بخواهیم از روش انتقال استفاده کنیم باید نمودار \( \Large y=-\left| x \right|  \) را رسم کرده و منتقل کنیم حال ما از هر دو روش آن را رسم می‌کنیم.

ریشه داخل قدر مطلق (\( \Large x \) راس)

\( \LARGE x=3 \rightarrow y=2 \)

راس \( \LARGE S:(3,2) \)

4	3	2	x
1	2	1	y

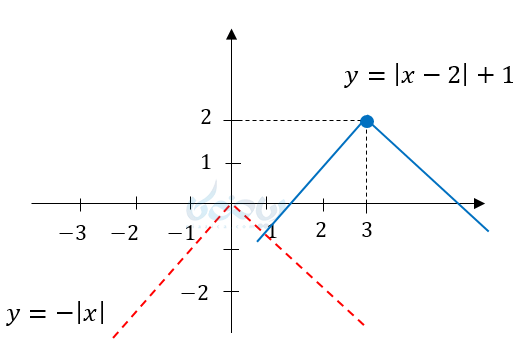
در این مثال در روش انتقال 3 واحد به راست و 2 واحد به بالا نمودار \( \Large y=-\left| x \right| \) را منتقل می‌کنیم.

 

در شکل زیر هم دو مثال از رسم نمودار تابع قدر مطلق برای شما آورده ایم .

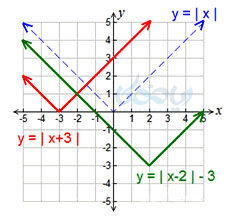
مثال ۸ از رسم نمودار تابع قدر مطلق: تابع \( \Large y=\left| 2x-1 \right|  \) را رسم کنید اگر \( \Large x \) ضریب داشته باشد حتما آن را از روش نقطه‌یابی رسم کنید.

حل ۸:

1	\( \Large \frac{1}{2} \)	0	x
1	۰	1	y

در این مثال برای راحتی کار ما نیم واحد قبل و بعد طول راس را به عنوان نقطه کمکی در نظر گرفتیم.

---

---

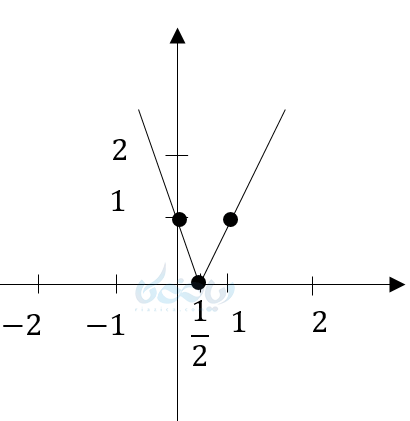
نکته رسم نمودار تابع قدر مطلق : دقت کنید اگر در تابع قدر مطلق ضریب \( \Large x=1 \) باشد زاویه بین هفت یا هشت، 90 درجه خواهد بود. اما اگر ضریب \( \Large x \) بیشتر از یک باشد دهانه نمودار بسته‌تر خواهد شد و زاویه بین دو خط از 90 درجه کمتر و اگر عددی بین صفر و یک باشد دهانه نمودار بازتر می‌شود و زاویه بین دوخط از 90 درجه بیشتر در این مثال دهانه بسته‌تر شد و از 90 درجه کمتر است.

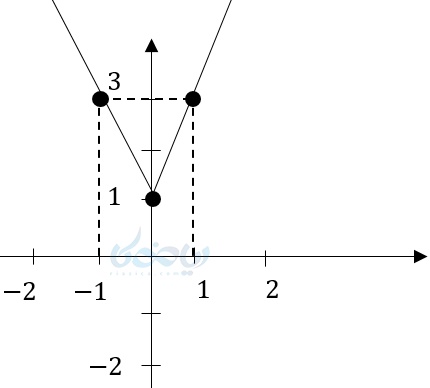
مثال ۹ از رسم نمودار تابع قدر مطلق: \( \Large y=2\left| x \right|+1  \) را رسم کنید.

حل ۹: ریشه داخل قدر مطلق (\( \Large x \) راس)

\( \LARGE x=0 \rightarrow y=1 \)

راس \( \LARGE S:(0,1) \)

1	۰	-1	x
3	1	3	y

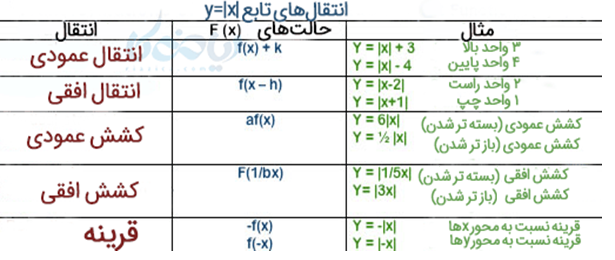
به طور کلی داریم:

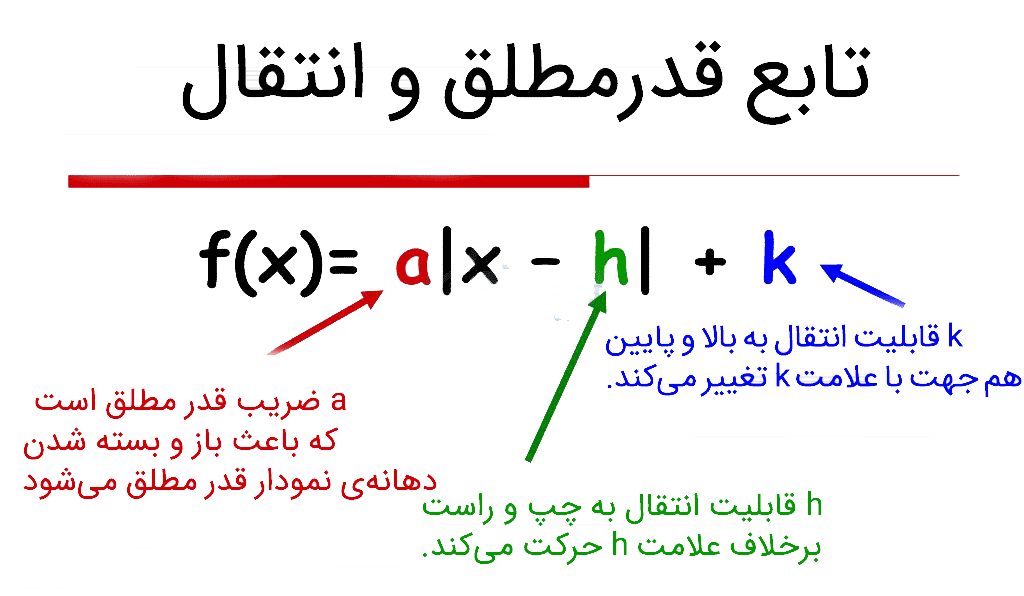
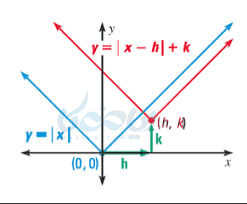
تمام آنچه تاید در مورد نمودار تابع قدر مطلق ساده باید بدانید در جدول زیر امده است

 

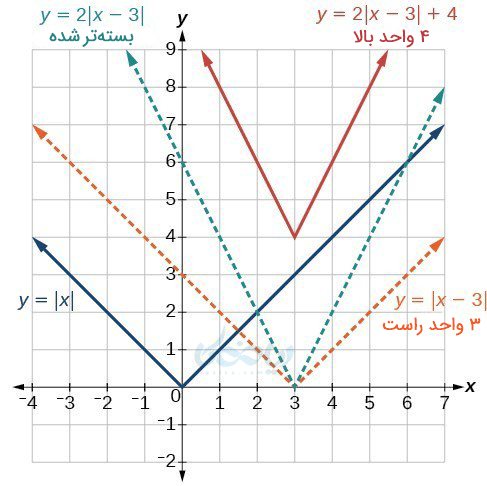
مراحل رسم نمودار تابع قدر مطلق \( \Large y=2\left| x-3 \right| +4 \) را در شکل زیر ببینید.

 

ویدیو از رسم تابع قدر مطلق به زبان شکل ها

در این ویدیو رسم تابع قدر مطلق به روش نقطه یابی و انتقال برای شما آورده شده است.

آخر کلاس رسم نمودار قدر مطلق

در این جلسه از آموزشهای ریاضی دهم در مجموعه ریاضیکا باهم در مورد تابع قدر مطلق و رسم نمودار تابع قدر مطلق صحبت کردیم. مثال‌های گوناگونی را باهم در این مورد حل کردیم و همین‌طور نمودارهای مختلفی را دیدیم.

در صورتیکه که هر گونه سوالی در رابطه با این مبحث داشتید، در انتهای همین مبحث در بخش دیدگاه‌ها مطرح کنید. ما در ریاضیکا به سوالات شما پاسخ خواهیم داد.

---

---

به خوندن ادامه بده!

تابع خطی به سادگی یک خط مستقیم 📈📏دامنه و برد تابع به زبان عکس‌ها ✅👨‍👧‍👧