آموزش ریاضی پایه دهم
آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!
فروردین
مهم‌ترین نکته‌ای که در آموزش آمار دهم می‌فهمیم کاربرد علم آمار است. از یک مغازه‌دار جزء گرفته تا یک سرمایه‌گذار بزرگ نیاز به اعداد و ارقام، علم آمار و نتایج گرفته شده از آن دارند. با این علم است که آن‌ها می‌توانند برای کار خود برنامه‌ریزی داشته باشند و مقدار سود و زیان خود را بررسی کنند.
بنابراین لزوم یادگیری آمار و علم آمار بر همه روشن است. ما در این بخش مقدمه‌ای کوتاه بر علم آمار و آمار و تعاریف خود از جامعه و نمونه و متغیرها ارائه می‌دهیم و بعد از آن با آموزش آمار ریاضی دهم در خدمت شما خواهیم بود.
تعریف آمار
آمار، مجموعه‌ای از اعداد، ارقام و اطلاعات است.
تعریف علم آمار
به مجموعه روش‌هایی که شامل:
- جمع آوری اطلاعات و اعداد و ارقام
- سازماندهی و نمایش آن‌ها
- تحلیل و تفسیر داده‌ها
- نتیجه‌گیری، قضاوت و پیش‌بینی مناسب در مورد پدیده‌ها
- آزمایش‌های تصادفی
می‌شود، علم آمار می‌گویند.
پس از تعاریف بالا متوجه این مطلب می‌شویم که آمار داده‌های خام را شامل می‌شود. اما با علم آمار روی این داده‌های خام چهار مرحله عملیات انجام می‌دهید تا این داده‌ها قابل استفاده و قضاوت شوند.
اگر بخواهیم مثالی ساده از کاربرد علم آمار داشته باشیم، می‌توانیم سازمان هواشناسی را مثال بزنیم. این سازمان دادههایی را به وسیله ایستگاه‌های هواشناسی خود در نقاط مختلف کشور دریافت می‌کند. در ادامه روی این داده‌ها (چهار مرحله علم آمار) کارهایی را انجام می‌دهد و وضع هوا را در چند روز آینده پیش‌بینی می‌نماید. با استفاده از خروجی این داده‌ها و علم آمار است که کشاورزان یا مسافرین یا حتی دست‌فروش‌ها برای کار خود طبق این پیش‌بینی‌ها برنامه‌ریزی می‌کنند.
جامعه و نمونه در آموزش آمار دهم
وقتی یک محقق می‌خواهد روی موضوعی کار کند باید افراد یا اشیائی که می‌خواهد روی آن‌ها این کار تحقیقی را انجام دهد مشخص نماید (جامعه مورد هدف). امّا گاهی کار روی کل جامعه هدف کاری زمان‌بر و هزینه‌بر خواهد بود. بنابراین به جای مطالعه روی کل جامعه، روی بخش از جامعه تحقیق خود را انجام می‌دهیم که به این بخش نمونه می‌گویند.
البته باید در انتخاب نمونه دقت داشت که نمونه مورد نظر بیانگر کل خصوصیات جامعه باشند. مثلاً اگر معلمی می‌خواهد روی علل افت نمره ریاضی دانش‌آموزان یک مدرسه کار کند، باید نمونه خود را از تمام کلاس‌ها انتخاب کرده و در گزینش دانش‌آموزان آن‌ها را به طور تصادفی انتخاب کند. در این حالت است که دانش‌آموزان انتخاب شده، بیانگر خصوصیات کل دانش‌آموزان مدرسه هستند. نه فقط از یک کلاس خاص که ممکن است شامل یکسری دانش‌آموز ضعیف یا قوی باشد.
تعریف جامعه در آموزش آمار دهم
مجموعه تمام افراد یا اشیایی که درباره یک یا چند ویژگی آن‌ها تحقیق انجام می‌گیرد جامعه یا جمعیت نامیده می‌شود. هر یک از این افراد یا اشیای یک عضو این جامعه نامیده می‌شوند.
تعریف نمونه در آموزش آمار دهم
به بخشی از جامعه که برای مطالعه و تحقیق انتخاب می‌شوند نمونه می‌گویند و به هر یک از افراد یا اشیای انتخاب شده عضو نمونه می‌گویند.
تعداد اعضای جامعه یا نمونه (حجم جامعه یا نمونه)
به تعداد اعضای جامعه یا نمونه اندازه جامعه یا نمونه یا حجم جامعه یا نمونه نیز گفته می‌شود.
مثلاً اگر مدرسه‌ای 200 دانش‌آموز داشته باشد که روی 20 نفر آن‌ها کار تحقیقی انجام می‌پذیرد اندازه جامعه 200 و اندازه نمونه 20 نفر میباشد.
مثال ۱: می‌خواهیم در مورد کیفیت محصولات باغی یک شهر تحقیقی انجام دهیم. اگر تعداد باغات این شهر 1000 باغ باشد و 100 قطعه باغ انتخاب شود با توجه به اطلاعات موجود جدول زیر را کامل کنید.
| ویژگی مورد بررسی | اندازه نمونه | اندازه جامعه | جامعه |
|---|---|---|---|
| کیفیت محصولات باغی | 100 | 1000 | باغات یک شهر |
متغیر و انواع آن (کمی و کیفی)
وقتی ما در مورد افراد یا اشیا تحقیق میکنیم، این افراد یا اشیاء دارای ویژگی‌های مختلف در ابعاد مختلف هستند. ما باید در ابتدا مشخص کنیم در مورد چه ویژگی این افراد یا اشیاء می‌خواهیم بررسی داشته باشیم.
مثلاً اگر دانش‌آموزان یک مدرسه را به عنوان جامعه انتخاب کرده‌ایم می‌توانیم روی علل افت تحصیلی در درس ریاضی یا قد و وزن یا علاقمندی‌ها و غیره تحقیق انجام دهیم. یا اگر روی محصولات باغی یک شهر بررسی انجام می‌دهیم، مثلاً در مورد سیب، می‌توانیم روی وزن یا اندازه یا مزه یا کیفیت این میوه بررسی کنیم.
این ویژگی‌های مورد بررسی گاهی به وسیله دستگاهی قابل اندازه‌گیری هستند. بعنوان مثال قد و وزن دانش‌آموزان یا ترازو یا متر قابل اندازه‌گیری است. امّا میزان علاقه آن‌ها به درس ریاضی یا کیفیت میوه سیب، یا مزه سیب (مقدار شیرینی و ترشی) به وسیله دستگاهی قابل اندازه گیری نیست. در این حالت خودمان برای آن‌ها میزان درجه‌ای مشخص میکنیم. مثلاً در مورد علاقمندی به درس ریاضی از گزینه (زیاد، متوسط، کم) استفاده میکنیم.
تعریف متغیر و مقدار متغیر در آموزش ریاضی دهم
متغیر، ویژگی از اعضای یک جامعه است که مورد تحقیق و بررسی و مطالعه قرار می‌گیرد. متغیر معمولاً از یک عضو به عضو دیگر تغییر می‌کند. عددی که به ویژگی یک عضو نسبت داده می‌شود، مقدار متغیر می‌شود.
مثال ۲ از آموزش آمار دهم : جدول زیر در نظر بگیرید.
| متغیرهای یک دانش‌آموز | مقدار متغیر |
|---|---|
| سن دانش‌آموز | 15 |
| نمره در ریاضی دهم دانش‌آموز | 17 |
| گروه خونی | A |
| قد دانش‌آموز | 160 |
| وزن دانش‌آموز | 60 |
| میزان علاقه به درس ریاضی | متوسط |
| رنگ چشم | مشکی |
به جدول بالا که دقت کنید. می‌بینید بعضی ویژگی‌ها قابل اندازه‌گیری هستند. مانند:
- سن
- نمره درس ریاضی
- قد
- وزن
ولی بعضی ویژگی‌ها قابل اندازه‌گیری نیستند. مانند:
- گروه خونی
- میزان علاقه به درس ریاضی
- رنگ چشم
پس ما نتیجه می‌گیریم دو نوع متغیر داریم:
- کمی
- کیفی
تعریف متغیر کمی
به متغیرهایی که قابل اندازه‌گیری هستند متغیر کمی می‌گویند. مانند قد، وزن، سن و ….
تعریف متغیر کیفی
متغیرهایی که قابل اندازه‌گیری نیستند را متغیر کیفی می‌گویند. مانند رنگ چشم، گروه خونی، کیفیت یک میوه، میزان علاقه به تلویزیون و غیره.
مثال ۳ از آموزش آمار دهم : تعیین کنید کدام از متغیرهای زیر کمی و کدام کیفی هستند.
| متغیر | نوع آن |
|---|---|
| تعداد مسافران یک قطار | کمی |
| اقوام ایرانی | کیفی |
| جنس افراد | کیفی |
| وزن افراد | کمی |
| رنگ موی افراد | کیفی |
| میزان علاقه به موسیقی پاپ | کیفی |
| میزان لذت بردن از آشپزی | کیفی |
| گروه خونی | کیفی |
| تعداد فرزندان | کمی |
| قد افراد | کمی |
آموزش آمار دهم و انواع متغیر کمی (پیوسته، گسسته)
دیدیم متغیرهای کمی قابل اندازه‌گیری هستند. حال فرض کنید وزن دانش‌آموزان پایه دهم مدرسهٔ رضوان را اندازه‌گیری کنیم. اگر کمترین وزن 42 کیلوگرم و بیشترین وزن 75 کیلوگرم باشد، می‌توانیم بگوییم وزن این دانش‌آموزان در بازه \( \Large [42,75] \) قرار دارد. یعنی هر عدد حقیقی از این بازه می‌تواند وزن دانش‌آموزی باشد. چون وزن آن‌ها همگی دقیقاً یک عدد صحیح نیست.
مثلاً وزن دانش‌آموزی می‌تواند \( \Large 52/5 \) یا \( \Large 64/2 \) و غیره باشد. یا به اصطلاح خودمانی اعداد خورده‌دار هم می‌توانند در این بازه باشند. در این صورت وزن دانش‌آموزان را متغیر کمی پیوسته می‌نمامیم.
حال تعداد دانش‌آموزان کلاس‌های مدرسه رضوان را در نظر بگیرید. فرض کنید کمترین تعداد دانش‌آموزان کلاس دهم ب 25 نفر و بیشترین تعداد دانش‌آموزان کلاس دوازدهم ج 35 نفر باشند. آیا باز مانند مثال بالا می‌توانیم بگوییم که تعداد دانش‌آموزان این مدرسه در بازه \( \Large [25,35] \) قرار دارند؟
همانطور که دقت کنید جواب منفی است. چون یک کلاس یا دقیقاً 27 نفر یا 28 نفر دانش‌آموز دارد. یعنی تعداد عضو‌های هر کلاس یک عدد صحیح خواهد بود. و به اصطلاح خورده و اعشاری ندارد. پس در این‌صورت می‌گوییم تعداد دانش‌آموزان هر کلاس یک مدرسه متغیر کمی گسسته است.
تعریف متغیر کمی پیوسته
متغیری که اگر دو مقدار \( \Large a,b \) را بتواند اختیار کند، هر مقدار در بازهٔ \( \Large [a,b] \) را نیز بتواند اختیار کند.
تعریف متغیر کمی گسسته
متغیری که پیوسته نباشد. یا به اصطلاح اگر دو مقدار \( \Large a,b \) را بتواند اختیار کند، هر عدد در بازه \( \Large [a,b] \) را نتواند اختیار کند.چنین متغیری را گسسته می‌نامند.
مثال ۴ از آموزش آمار دهم: در جدول زیر نوع متغیرهای کمی را مشخص کنید.
| متغیر | نوع آن |
|---|---|
| وزن سیب | پیوسته |
| اندازه طول بدن شیر | پیوسته |
| دمای هوا در قله | پیوسته |
| فشار هوا در قله | پیوسته |
| تعداد روزهای آفتابی تهران | گسسته |
| جمعیت شهرهای ایران | گسسته |
| سن افراد | پیوسته |
| قد افراد | پیوسته |
| شاخص توده بدن | پیوسته |
| تعداد دوستان شما | گسسته |
انواع متغیرها کیفی (اسمی-ترتیبی) در آموزش آمار دهم
گفتیم متغیرهای کیفی قابل اندازه‌گیری نیستند و آن‌ها را با عدد نشان نمی‌دهند. در کل می‌توان متغیرهای کیفی را به دو دسته تقسیم کرد:
- کیفی ترتیبی
- کیفی اسمی
۱. تعریف متغیر کیفی ترتیبی
دسته اول متغیرهای کیفی ترتیبی هستند که در آن‌ها ترتیب طبیعی وجود دارد. بعنوان مثال:
- میزان تحصیلات یک فرد (بی‌سواد، دیپلم، فوق دیپلم، کارشناسی، کارشناسی ارشد، دکترا)
- میزان علاقهٔ شما به موسیقی (کم، متوسط، زیاد)
- میزان هوش افراد (هوش بالا، متوسط، پایین)
- دوران زندگی یک فرد (کودکی، نوجوانی، جوانی، میانسالی، کهنسالی)
۲. تعریف متغیر کیفی اسمی
متغیری که در آن هیچ نوع ترتیب خاصی وجود ندارد. بعنوان مثال:
- رنگ چشم افراد (مشکی، قهوه‌ای و …)
- گروه خونی افراد (\( \Large A,B,AB,O \))
- جنسیت افراد (دختر و پسر)
همانطور که مشاهده میکنیم هیچ ترتیبی در این مثال‌ها وجود ندارد.
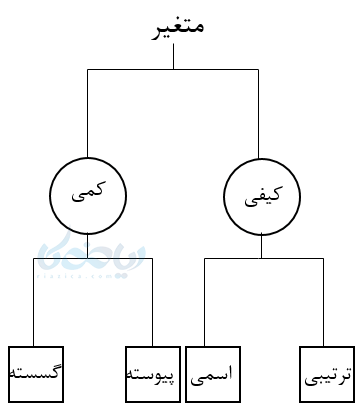
نکته آموزش آمار دهم : پس می‌توانیم متغیرها را با نمودار زیر نمایش دهیم.
در جدول زیر نوع متغیرها را مشخص کنید.
| متغیر | نوع آن |
|---|---|
| مقام یک ورزشکار | کیفی ترتیبی |
| میزان علاقه شما به یک غذا | کیفی ترتیبی |
| گروه خونی افراد | کیفی اسمی |
| قد افراد | کمی پیوسته |
| اقوام ایرانی | کیفی اسمی |
| نمره ریاضی ترم اول | کمی پیوسته |
| انواع وضعیت آب و هوا | کیفی اسمی |
| نوع بارندگی | کیفی اسمی |
| شدت بارندگی | کیفی ترتیبی |
| میزان بارندگی یک شهر در یک سال | کمی پیوسته |
| میزان هوش افرادا | کیفی ترتیبی |
| میران تحصیلات افراد | کیفی ترتیبی |
| سرعت یک خودرو | کمی پیوسته |
| تعداد ماهی‌های دریا | کمی گسسته |
زنگ آخر کلاس آموزش آمار دهم
در این آموزش از سری آموزش ریاضی دهم از ریاضیکا، سعی کردیم آموزش ریاضی دهم را همراه با مثال‌ها، اشکال متنوع و جدول‌های مختلف برای شما عزیزان بیان کنیم.
هرچه سوال از این نوشتار داشتید، در زیر همین قسمت در بخش دیدگاه‌ها برای ما بنویسید. کارشناسان ریاضیکا حتماً به سوالات شما پاسخ می‌دهند.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی دهم به شما پیشنهاد می‌دهیم:
- متمم یک مجموعه و تعداد عضو‌های اجتماع دو مجموعه 2️⃣♓️
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
عالی توضیح دادید
انواع متغیرها رو نمیدونستم ممنون که راهنمایی کردید
ممنون دوست عزیز
خوشحالیم که راضی بودید
اگر اخر درسنامه (منظورم فقط این مبحث نیست کلن همه درسا که درس میدید) دو سه تا نمونه تست هم بزارین خیلی بهتر میشه
با عرض سلام
ممنون از پیشنهاد شما حتما در ادیتها لحاظ میکنیم
با سلام و عرض تشکر بابت مجموعه خوب آموزشی، در مورد مبحث متغیرها در آمار، در کتاب جدید تقسیم بندی و اسامی و تعاریف به این شکل نیست ولی دسته بندی به همین شکله.. آیا نسخه به روز شده بر اساس کتاب جدید رو هم دارید؟
یا سلام وعرض ادب
دوست عزیز این مطلب بر اساس کتای دهم امسال میباشد وبه روز هست
تعریف هاتون درست بود ولی اون قسمت هایی که گفته بودیم عدد خرده دار و بدون خرده و اینا توی کتاب درسی ذکر نشده ولی خب کمک زیادی به بچه ها میکنه
سلام تشکر بابت مجموعه خوب آموزشی
واقعا عالی بود انواع متغیر هارو بلد نبودم الان خیلی خیلی خوب متوجه شدم بازم ممنون
با سلام واحترام
ممنون از نگاه شما خوشحالیم که مفید واقع شده
سلام واقعا عالی بود ممنونم بابت آموزش خوب تون??
سلام خداقوت
امکانش هست یک توضیحی درباره نمره ترم اول یا نمره ریاضی پایه نهم بدید که این دو کمی گسسته هستن یا پیوسته؟ چون من تو یه کتاب دیدم نوشته بود گسسته ولی شما پیوسته زدید…
با سلام دوست عزیز
پیوسته هست چون نمره میتونه خورده هم داشته باشه
ولی هر خورده ای نمیتونه باشه و حتما مضربی از 0.25 هستش
پس کمی گسسته صحیح هستش
ولی مثلا برای معدل که هر خورده ای میتونه باشه اونجا صحیح اینه که بگیم کمی پیوسته
چرا نمیتونه ؟ثانیه خودش به صدم وهزارم …ثانیه قبل تقسیم ومحاسبه هست همین که خورده میگیره یعنی گسسته اگه هر کس میزان عمرش دقیقا یکسال یا دو سال یا چند سال بود میشد پیوسته
منظورم مثال نمره ریاضی بود…
نه سن
فکر کنم اشتباه متوجه شدید
چکونه سن کمی پیوسته میشه مگه نباید کمی گسسته باشه؟
سلام دوست عزیز در این زمان دقیقا سن شما مثلا پانزده ساله یا پانزده سال وشش ما سه روز و ۸ساعت
پس سن کمی پیوسته هست هر ثانیه که میگذره یک ثانیه به عمر شما اضافه میشه پس سن یک نفر یه عدد حقیقی بین صفر تا زمان کنونی میباشد
ولی هر خورده ای نمیتونه باشه و مضربی از 0.25 هستش
پس میشه کمی گسسته
از وقتی که سایت شمارو پیدا کردم دیگه دور هر جزوه ای رو خط کشیدم….
بدون اغراق میگم که اینقد جزوه های شما کامله
من همینارو میخونم هر امتحان سخت و آسونی از ریاضی رو ۲۰ میشم
و ضمنا استاد ریاضی ما همیشه براش سواله من که سرکلاس یک کلمه هم جزوه نمی نویسم 😅
چطور امتحانامو خوب میدم؟
فقط به خاطر اینکه دلم به جزوه های شما خوشه و میدونم شما کامل ترین آموزش هارو در اختیار ما قرار دادید بعضی از دوستام هم که ازم پرسیدن چطور ریاضیم خوبه سایت شمارو معرفی کردم و اوناهم مثل من عاشق ریاضی و جزوات شما شدن . شما بهترین هستید و خواهید بود و قطعا محبوبیت اتفاقی نیست . امیدوارم در هر زمینه ای با این همه تلاش و استعدادتون به نهایت رشد،و کمال برسید . موفق و موید باشید استادان گرامی و گرانقدر
از طرف دانش آموز کوچک شما💌 مواظب خودتون باشید که بهترین در ایران هستید …
سلام به شما دختر خوبم
ممنون از انرژی که به ما می دهید من وقتی کامنتهای اینچنینی رو میخونم خدا رو شکر میگم که به رسالتم که آموزش دانش آموزان سرزمینم هست دست پیدا کردم و تونستم تجربیات سی وسه ساله خودم در امر آموزش رو به تمام بچه های ایران تقدیم کنم ممنون از نگاه گرم شما