آموزش ریاضی پایه دهم
تابع چند جمله ای به زبان ساده ✖️🔤
اسفند
قبل از شروع بحث تابع چند جمله ای باهم مطالب اولیه آن را فرامی‌گیریم تا تمامی مطالب را به طور آسان و شیوا در ذهن داشته باشیم.
یک جمله ای
یک جمله‌ای بر حسب متغیر \( \Large x \) به صورت \( \Large ax^n \) نمایش داده می‌شود. در این عبارت یک جمله ای \( \Large a \) یک عدد حقیقی است که ضریب نام دارد. \( \Large n \) یک عدد حسابی است (شامل صفر و اعداد طبیعی) که اگر \( \Large n \) صفر باشد چون توان صفر برابر یک است، یعنی جمله ما فقط از یک عدد تشکیل می‌شود. پس نتیجه می‌گیریم اعداد نیز جزء یک جمله ای ها هستند.
نکته ۱: یک جمله‌ای‌ها می توانند از یک یا چند متغیر تشکیل شوند .
نکته ۲:با توجه به تعریف یک جمله ایها متغیر نمی تواند زیر رادیکال یا در مخرج یا داخل قدر مطلق باشد.
مثال ۱: تعیین کنید کدام یک از عبارات زیر یک جمله‌ای است؟
حل ۱:
(1
\( \LARGE 78x^2y^{-2} \)
یک جمله‌ای نیست.
(2
\( \LARGE \frac{58}{x^3+9} \)
یک جمله‌ای نیست.
(3
\( \LARGE 84x^3 \)
یک جمله‌ای است.
(4
\( \LARGE \frac{1}{5}a^2b^3c^5d \)
یک جمله‌ای است.
(5
\( \LARGE \sqrt 3 xyz \)
یک جمله‌ای است.
(6
\( \LARGE \sqrt {5x} \)
یک جمله‌ای نیست.
جملات متشابه عبارت‌های جبری
وقتی دو یک جمله‌ای متغیر و درجه‌شان با هم برابر باشد، می‌گوییم این جملات با هم متشابه هستند. به مثال‌های زیر دقت کنید که همگی متشابه‌اند.
(1
\( \LARGE 3x^2y^3 , -\frac{1}{2}x^2y^3 \)
(2
\( \LARGE 5abc , \sqrt 2 abc \)
(3
\( \LARGE 4x^3 , -7x^3 \)
(4
\( \LARGE 7xy^2,-11y^2x \)
اما جملات زیر متشابه نیستند.
(1
\( \LARGE 7x^2y^3,-5x^3y^2 \)
(2
\( \LARGE \frac{1}{5}ab,\frac{1}{7}abc \)
(3
\( \LARGE 4x^3 , 7x^2 \)
جمع و تفریق یک‌جمله ای ها
جملات متشابه را می‌توان با هم جمع و تفریق کرد. ولی جملات غیرمتشابه را نمی‌توان با هم جمع و تفریق کرد. در جمع و تفریق جملات متشابه ضرایب با هم جمع و تفریق می‌شوند.
مانند:
(1
\( \LARGE 5x^2y+7x^2y \)
\( \LARGE =12x^2y \)
(2
\( \LARGE 8x^3y^2z-10x^3y^2z \)
\( \LARGE =-2x^3y^2z \)
(3
\( \LARGE 5abc-7abc-\frac{1}{2}abc\)
\( \LARGE =-\frac{5}{2}abc \)
نکته ۲: در ضرب یک‌جمله ای ها احتیاجی به متشابه بودن جملات نیست.
نکته ۳: در جمع و تفریق چند جمله ای ها یا برای تعیین تعداد جملات و درجه چند جمله ای ها اگر چند جمله متشابه داشته باشیم، ابتدا آن‌ها را با هم جمع و تفریق می‌کنیم. (ساده کردن) سپس تعداد جملات یا درجه عبارت را مشخص کنیم.
چند جمله ای
چند جمله ای از مجموع ،چند یک جمله ای تشکیل می‌شود. پس در اینجا نیز توان متغیر فقط عدد حسابی می‌تواند باشد.
نکته ۴: با توجه به تعریف یک جمله‌ای، در چندجمله‌ای‌ها متغیر نمی‌توان در مخرج یا زیر رادیکال باشد و می تواندشامل یک یا چند متغیر باشد.
تشخیص تعداد جملات در چند جمله ای ها
با تعداد جملاتشان می‌توان آن‌ها را تشخیص داد.
نکته ۵: ابتدا باید چندجمله‌ای را به ساده ترین حالت ممکن نوشت سپس تعداد جملات را مشخص کرد.
مثال ۲: به مثال‌های زیر توجه کنید.
(1
\( \LARGE 2 \)
یک جمله‌ای.
(2
\( \LARGE 25xy+9 \)
دو جمله‌ای.
(3
\( \LARGE 84x^3+9y+88 \)
سه جمله‌ای.
نکته ۶: چند جمله ای ها می‌توانند متغیر نداشته باشند \( \Large 65 \)، یا یک متغیر داشته باشند \( \Large x^5 \)، یا بیشتر \( \Large xrtyu \)
درجه چند جمله ای
بزرگترین توان یک چند جمله ای (بر حسب یک متغیر خاص) همان درجه آن چند جمله ای است.
نکته ۷: ابتدا باید چند جمله ای را به ساده‌ترین حالت ممکن نوشت سپس درجه چند جمله ای را مشخص کرد.
مثال ۳:
(1
\( \LARGE 4x^2+5x^5+9x^8 \)
درجه چند جمله ای بزرگترین توان یعنی 8 است .
(2
\( \LARGE 3x^5x^4 \)
درجه چند جمله ای بزرگترین توان (بعد از ساده شدن) یعنی جمع توان \( \Large x \)ها یعنی 9 است.
\( \LARGE 3x^9 \)
فرم استاندارد در چند جمله ای ها
یعنی جملات را بر حسب یک متغیر از توان بیشتر به کوچک مرتب کنیم.
مانند:
\( \LARGE 5x^3 + 3x^7 +9 -9x^2 \)
فرم استاندارد
\( \LARGE 3x^7 + 5x^3 -9x^2 +9 \)
مثال ۴: فرم استاندارد توابع زیر را بنویسید.
(1
\( \LARGE -9x^5 +97x^9-9+ 87x \)
فرم استاندارد
\( \LARGE 97x^9-9x^5+ 87x-9 \)
(2
\( \LARGE -25x^2 +x^4+ 87x^6 \)
فرم استاندارد
\( \LARGE 87x^6+x^4-25x^2 \)
(3
\( \LARGE 5x^4-9x^8 -8 \)
فرم استاندارد
\( \LARGE- 9x^8 +5x^4 -8 \)
اعمال روی چند جمله ای
بین دو چند جمله ای می‌توان جمع و تفریق و ضرب و تقسیم را اعمال کرد.
جمع و تفریق چند جمله ای ها
جمع
وقتی چند جمله ای ها با هم جمع می‌شوند جملات متشابه را با هم ساده می‌کنیم. یعنی با توجه به علامت ضرایب آن‌ها جمع می‌شوند. درنهایت جواب به صورت استاندارد (از توان بزرگ به کوچک) نوشته می‌شود.
مثال ۵:
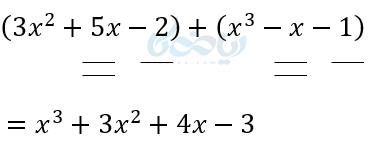
می‌توان برای راحتی کار ابتدا چند جمله ای ها را به صورت ستونی زیر هم نوشت سپس با هم جمع کرد.
مثال ۶:
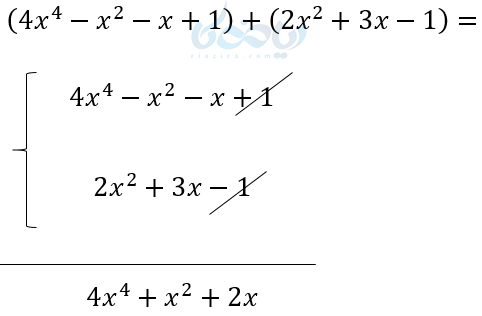
تفریق چند جمله ای
در مورد تفریق، چند جمله ای دوم را قرینه کرده سپس جملات مشابه را جمع می‌کنیم. درنهایت جواب را به صورت استاندارد می‌نویسیم.
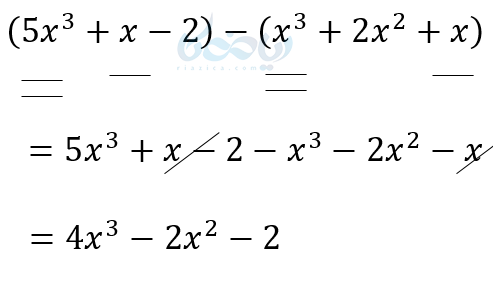
در اینجا هم می‌توانیم ابتدا آن‌ها را ستونی نوشته و در عین حال جملات چند جمله ای دوم را قرینه کنیم.
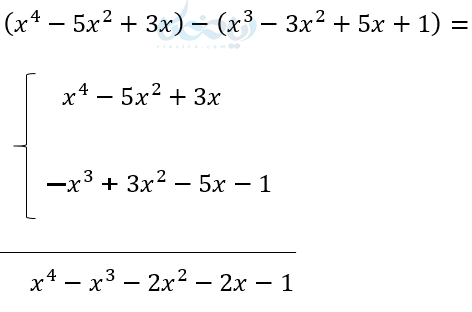
ضرب و تقسیم چند جمله ای ها
ضرب چند جمله ای ها
-
ضرب یک جمله در یک جمله
وقتی یک، یک جمله ای در یک جمله ای دیگر ضرب می‌شود، ضرایب در هم ضرب شده و متغیرها هم در هم ضرب می‌شوند. طبق قانون اعداد توان‌دار، اعداد با پایه‌های مساوی توان‌هایشان با هم جمع می‌شوند و جواب همیشه باز یک، یک جمله‌ای می‌شود.
(1
\( \LARGE 5a^3b^2 \times 3a^2b^4c \)
\( \LARGE =15a^5b^6c \)
(2
\( \LARGE 7x^2 \times 4x^3yz \)
\( \LARGE =28x^5yz \)
-
ضرب یک جمله در چند جمله ای
اگر یک، یک جمله ای در چند جمله ای ضرب شود. یک جمله ای در تک تک جملات چند جمله ای ضرب می‌شود و در نهایت تعداد جملات همان تعداد جملات چند جمله ای خواهد بود.
(1
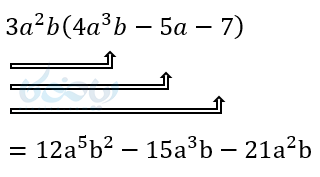
(2
-
ضرب چند جمله ای در چند جمله ای
وقتی یک چند جمله ای در یک چند جمله ای دیگر ضرب می‌شود، تک تک جملات این چند جمله ای ها در هم ضرب می‌شوند. در این حالت تعداد جملات اولیه به اندازه حاصل‌ضرب تعداد جملات است. یعنی وقتی دو جمله ای در سه جمله ای ضرب می‌شود. ابتدا تعداد جملات \( \Large 2 \times 3 =6 \) خواهد بود. البته ممکن است بعضی جملات متشابه باشند و در نهایت تعداد جملات کمتر شود.
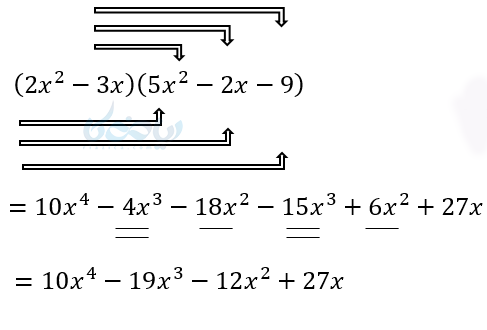
تقسیم چند جمله ای ها
وقتی دو چند جمله ای را میخواهیم به یکدیگر تقسیم کنیم، ابتدا آن‌ها را به صورت استاندارد در می‌آوریم. سپس مانند تقسیم دو عدد به هم عمل می‌کنیم به این صورت:
- چندجمله ای مقسوم را به جمله اول مقسوم علیه تقسیم کرده و جواب را در خارج قسمت می‌نویسیم.
- جواب را در مقسوم علیه ضرب کرده و قرینه آن‌ها را زیر مقسوم نوشته و ساده می‌کنیم.
- اگر درجه عبارت جبری باقیمانده از درجه مقسوم علیه کمتر بود کار تمام است اما اگر مساوی یا بیشتر بود عملیات بالا را دوباره تکرار می‌کنیم. آنقدر که درجه باقیمانده از درجه مقسوم علیه کمتر شود.
مثال ۷:
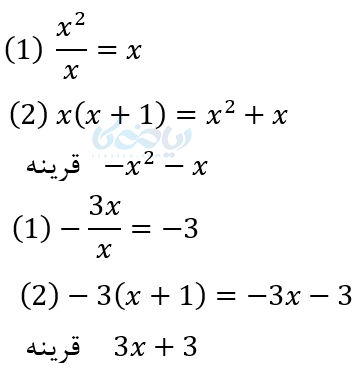
نکته ۸: اگر مانند مثال بالا باقیمانده صفر شود یعنی این دو عبارت به هم بخش‌پذیرند، یعنی را داریم:
\( \LARGE \frac{x^2-2x-3}{x+1}=x-3 \)
یا
\( \LARGE (x+1)(x-3) \)
\( \LARGE =x^2-2x-3 \)
نکته ۹: یکی از روش‌های تجزیه عبارت‌های جبری در صورتی که یکی از عامل‌ها را داشته باشیم عمل تقسیم چندجمله‌ای‌ها است.
مثال ۸:
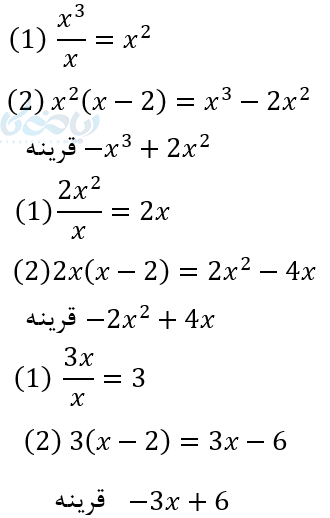
نکته ۱۰: البته نوشتن این مراحل برای شما لازم نیست و با تمرین کردن همه مراحل را می‌توانید ذهنی انجام دهید.
در این مثال مشاهده می‌کنیم 3 مرحله داشتیم ولی به باقیمانده صفر نرسیدیم. ولی درجه باقیمانده کمتر از درجه مقسوم علیه است. (درجه باقیمانده صفر، درجه مقسوم علیه یک)
امتحان تقسیم چند جمله ای ها
برای اطمینان از درست عمل کردن، عملیات تقسیم می‌توانیم به صورت زیر عمل کنیم.
در مثال بالا داریم:
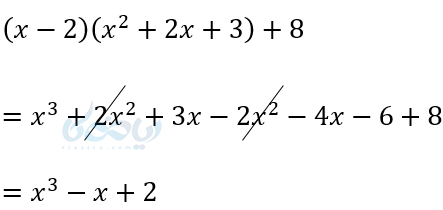
مثال ۹: اگر بدانیم \( \Large x^3 -1 \) بر \( \Large x-1 \) بخش‌پذیر است عامل دیگر را بیابید.
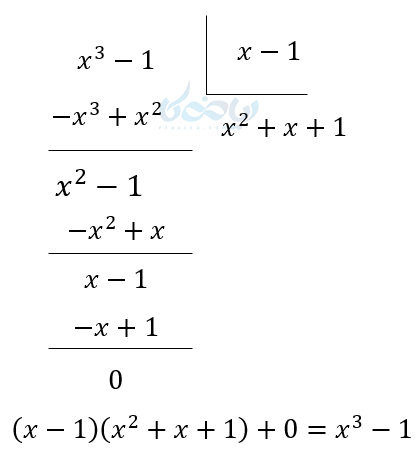
پس عامل دیگر \( \Large x^2+x+1 \) است.
تابع چند جمله ای
توابعی را که نمایش جبری آن‌ها، چند جمله ای های جبری از یک متغیر هستند، تابع چند جمله ای می‌نامیم.
تمامی مثال‌های زیر نمونه‌هایی از تابع چند جمله ای هستند.
\( \LARGE f(x)=2x^2+5x-1 \)
\( \LARGE g(x)=4x^3-3 \)
\( \LARGE h(a)=a^4-2a^2-4 \)
بزرگترین دامنه ممکن تمام تابع چند جمله ای \( \Large \mathbb{R} \) است. ولی برد تابع چند جمله ای به نوع چند جمله ای بستگی دارد.
نکته ۱۱: منظور از بزرگترین دامنه ممکن این است که گاهی تابعی را به ما می‌دهند و در دامنه‌ای خاص آن را در نظر می‌گیرند. ولی اگر ضابطه یک تابع را داشته باشیم بزرگترین دامنه ممکن آن مقادیری است که می‌توان به جای \( \Large x \) قرار دارد. در این حالت تابع به ازای آن مقادیر با معنی و تعریف شده باشد.
فرم کلی تابع چند جمله ای
\( \LARGE f(x)= \)
\( \LARGE a_0x^n+a_1x^{n-1} \)
\( \LARGE +a_2x^{n-2}+…+a_n \)
که در آن \( \Large a_0,a_1,…,a_n \) اعداد حقیقی و \( \Large n \) عدد حسابی هستند.
کلام آخر در آموزش تابع چند جمله ای
در بحث تابع چند جمله ای باهم از تعاریف اولیه تا خود تابع، به همراه مثال و شکل این توابع را دیدیم. در صورتیکه هر گونه سوالی از این نوشتار آموزشی داشتید، آن را در بخش دیدگاه‌ها در پایین همین بخش مطرح کنید. گروه آموزشی ریاضیکا حتما به سوال‌های شما پاسخ می‌دهند. شاد و پیروز باشید 🙂
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی دهم به شما پیشنهاد می‌دهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثال‌های متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!
عالی بود
ممنون از بذل توجه شما
سلام عالی بود
سلام ممنون از نظر لطف شما