آموزش ریاضی پایه دهم
اصل شمارش ، بدون شمردن ✖️🚫
ترتیبی که برای خواندن درسنامههای آموزش ریاضی دهم به شما پیشنهاد میدهیم:
- آموزش الگو و دنباله به راحتی آب خوردن ⚛️📶!
- متمم یک مجموعه و تعداد عضوهای اجتماع دو مجموعه 2️⃣♓️
- آموزش فاکتوریل – قدرتتو چند برابر کن❗️❗️❗️
- صفر تا صد توان های گویا 0️⃣💯 تنها آموزشی که باید بخوانید!
- اتحادهای جبری 6 رابطهٔ داغِ داغ 6️⃣🌞
- آموزش دنباله حسابی 🧮🔢 – از همیشه سادهتر؟
- مفهوم مجموعه در ریاضی را با ما ساده بیاموزید!?🅰️🔃
- تعیین علامت عبارت های جبری به زبان ساده ➕ ➖
- آموزش نسبتهای مثلثاتی: توضیحات کامل 📶✅همراه با تصویر
- دایره مثلثاتی یا دایره واحد : از 🅾️صفر تا 💯 صد
- محاسبه مساحت بدون داشتن ارتفاع🔺✏️ – چیزی شبیه معجزه
- روابط بین نسبت های مثلثاتی : 🎓⚙️ یاد بگیرید، حفظ کنید، ۲۰ بگیرید!
- آموزش دنباله هندسی 💎📶 – دنباله را اینجا دنبال کنید!
- تابع خطی به سادگی یک خط مستقیم 📈📏
- رسم نمودار تابع قدر مطلق به زبان شکلها 📒📉
- دامنه و برد تابع به زبان عکسها ✅👨👧👧
- تابع همانی – همان آموزشی که دنبالش بودید↔️💯
- تجزیه عبارت های جبری به 4 روش مختلف 4️⃣❗️
- عبارت های گویا ➗🚰به سادگی آب خوردن
- تابع چیست ؟👾⭕️ تمام آنچه باید بدانید.
- آموزش ریشه گیری در ریاضی دهم : زیر رادیکال نمون 🏖☑️ !
- گویا کردن مخرج گنگ 🚰🤐 مثل آب خوردن!
- آموزش ترکیب – ۸ قانون واجب که باید بدانید⚠️8️⃣
- آموزش حل معادله درجه دو + 4 روش مختلف حل آن4️⃣📝
- آموزش رسم سهمی به همراه ۲ روش کاربردی ⚙️✌️
- آموزش حل نامعادله همراه با رسم نمودار و مثالهای متنوع↪️📝
- تابع چند جمله ای به زبان ساده ✖️🔤
- تابع ثابت را در حافظه خود ثابت کنید 📊📐
- رسم سهمی با روش انتقال به سادگی آب خوردن!➡️📈
- تابع چند ضابطه ای را یکبار برای همیشه یاد بگیرید 📝📚
- تابع گویا – گویاتر از همیشه یاد بگیر ♨️➗
- اصل شمارش ، بدون شمردن ✖️🚫
- آموزش جایگشت یا جابجایی 🔁❗️ مفهومیترین آموزش
- آموزش احتمال دهم – کاملترین و جامعترین آموزش 🔣❓
- آموزش آمار ریاضی دهم 🔢〽️ تنها آموزش آمار که باید بخوانید!
در این نوشتار از مجموعه ریاضیکا میخواهیم باهم در مورد اصل شمارش که جزئی از درسهای آموزش ریاضی دهم است صحبت کنیم. به نظر میرسد شمارش کاری ابتدایی و ساده است. ولی در عمل با مسائل پیچیده شمارش برخورد میکنیم. حتی در زندگی روزمره و مسائلی که هر روز با آنها رو به رو میشویم.
یک مقدمه کوتاه از اصل شمارش
بیایید چند مثال جالب را باهم بررسی کنیم:
- آیا تا کنون به این فکر کردهاید با توجه به نوع شمارهگذاری کنونی اتومبیلها در ایران، اداره راهنمایی و رانندگی برای چند ماشین میتواند پلاک صادر کند و چرا هر چند سال یکباره این شیوه تغییر میکند؟
- سازمان ثبت و احوال ایران چند کد ملی 10 رقمی میتواند برای افراد مختلف صادر کند؟
- در تهران اداره مخابرات چند شماره تلفن ثابت یا تلفن همراه میتواند واگذار کند؟ و چرا هر چند سال یکبار تعداد ارقام تلفن های ثابت و یا پیش شماره تلفنهای همراه تغییر میکند؟
- شما برای کارت بانکی خود چند رمز چهاررقمی میتوانید انتخاب کنید؟
- حتی اگر شما چند دست لباس (کت و شلوار و کفش، مانتو و روسری) دارید، به چند صورت میتوانید آنها را بپوشید؟
و البته هزاران سوال مشابه دیگر نیز وجود دارد. در این بخش (اصل شمارش) به شما کمک میکنیم تا به همه این سوالات به راحتی و با کمی دقت و تفکر و تجزیه و تحلیل مسائل جواب دهید.
اصل شمارش: اصل جمع
اگر عملی را بتوان به دو روش انجام داد و برای انجام دادن عمل اول \( \Large n \) روش و برای انجام عمل دوم \( \Large m \) روش وجود داشته باشد، برای انجام کار مورد نظر \( \Large n+m \) حالت وجود دارد.
مثال 1: فرض کنید مادر شما با توجه به مواد اولیه موجود در خانه میتواند برای نهار خورشت یا آش تهیه کند. او با این مواد 3 نوع چلوخورشت (قیمه، قورمهسبزی و فسنجان) و یا دو نوع آش (جو و آش رشته) میتواند درست کند. مادر شما چند انتخاب دارد؟
حل 1:
\( \LARGE 2+3=5 \)
تعمیم اصل جمع
اگر عملی را بتوان به \( \Large k \) روش انجام داد و به طوریکه برای انجام عمل اول \( \Large m_1 \) روش و برای عمل دوم \( \Large m_2 \) روش ….. و برای عمل \( \Large k \) ام \( \Large m_k \) روش وجود داشته باشد، برای انجام کار مورد نظر \( \Large m_1 + m_2 + … + m_k \) روش وجود دارد.
مثال 2: علی میخواهد فرزندانش را به گردش ببرد. او قصد دارد آنها را به سینما یا پارک یا موزه ببرد. اگر در شهر آنها 5 سینما، 3 پارک و 2 موزه وجود داشته باشد، او چند انتخاب برای گردش فرزندانش دارد؟
حل 2:
\( \LARGE 5+3+2=10 \)
اصل شمارش: اصل ضرب
اگر انجام کاری شامل دو مرحله باشد، به قسمی که برای انجام مرحله اول کار \( \Large m \) انتخاب و برای هر کدام از این \( \Large m \) انتخاب در مرحله دوم \( \Large n \) انتخاب دیگر داشته باشیم، در کل کار مورد نظر با \( \Large m \times n \) روش قابل انجام است.
مثال 3: فرض کنید شما 3 عدد پیراهن و 2 شلوار به رنگهای مختلف دارید. به چند صورت میتوانید آنها را بپوشید؟ پیراهن (مشکی،قهوهای و آبی) شلوار (طوسی و قرمز)
حل 3:
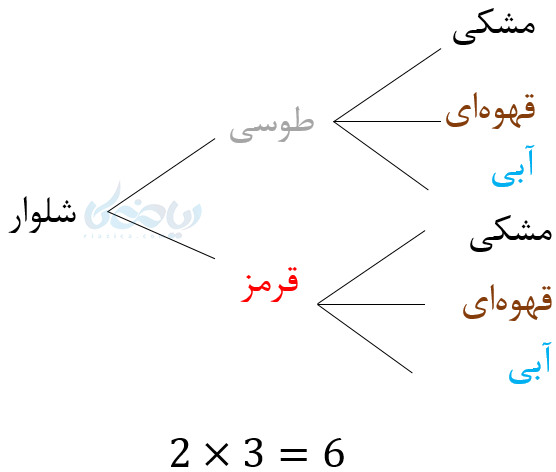
به ازای هر شلوار 3 پیراهن داریم. پس به شش صورت میتوانیم آنها را بپوشیم.
نکته ۱: نمودار درختی در حل مسائل میتواند به ما کمک کند.
تعمیم اصل ضرب
اگر کاری شامل \( \Large k \) مرحله باشد، به طوریکه برای انجام مرحله اول \( \Large m_1 \) روش و برای انجام مرحله دوم \( \Large m_2 \) روش و …… و برای انجام مرحله \( \Large k \)ام، \( \Large m_{12} \) روش وجود داشته باشد، پس این کار به \( \Large m_1 \times m_2 \times … \times m_k \) روش قابل انجام است.
مثال 4: شما برای کارت بانکی خود چند رمز (چهاررقمی) مختلف میتوانید تعریف کنید؟
حل 4: برای رقم اول ما 10 انتخاب. به ازای این ده انتخاب برای رقم دوم نیز ده انتخاب که میشود 100 انتخاب. به ازای این 100 انتخاب برای رقم سوم نیز 10 انتخاب که میشود 1000 انتخاب. و به ازای هر کدام از این 1000 انتخاب برای رقم چهارم نیز 10 انتخاب داریم. یعنی در کل 10000 انتخاب خواهیم داشت که این موضوع را به صورت زیر نشان میدهیم:

نکته ۲: گاهی در حل مسائل اصل شمارش هم از اصل ضرب و هم اصل جمع با هم استفاده میکنیم.
مثال 5: برای نوشتن یک رمز 3 رقمی از حروف فارسی یا اعداد غیر صفر استفاده میکنیم. به چند طریق این کار ممکن است؟ (اعداد یا ارقام تکراری نباشند.)
حل 5:
حالت اول: اگر در رمز از حروف فارسی غیرتکراری استفاده کنیم، داریم:
\( \LARGE 32 \times 31 \times 30 = 29760 \)
حالت دوم: اگر از اعداد غیر صفر (غیر تکراری) استفاده کنیم:
\( \LARGE 9 \times 8 \times 7 = 504 \)
پس تمام تعداد حالات ممکن \( \LARGE 29760 + 504 = 30264 \) است.
چند مثال جذاب از اصل شمارش برای فهم بیشتر
حال به چند سوال که در مقدمه مطرح کردیم، پاسخ دهیم:
مثال 6: سازمان ثبت و احوال چند کد ملی 10 رقمی میتواند صادر کند؟
حل 6:

یعنی برای 10 میلیارد نفر میتواند کد ملی صادر کند. لازم به ذکر است سه رقم اول کد ملی هر شخص به با توجه به محل تولدش انتخاب میشود.
مثال 7: با توجه به اینکه شماره تلفنهای ثابت در تهران هشت رقمی است و دو رقم اول آنها یکسان است، مخابرات در تهران چند شماره تلفن ثابت میتواند واگذار کند؟ (پیش شماره صفر و یک و نه نداریم)
حل 7:
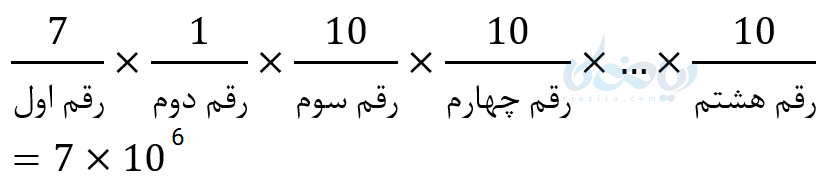
برای رقم دوم در این مثال فقط یک انتخاب داریم چون هر عددی که برای اولین رقم انتخاب کنیم همان را برای رقم دوم نیز باید انتخاب کنیم.
حال در مییابیم چرا تا چند سال پیش شماره تلفنهای تهران 6 رقمی بود و بعد هشت رقمی شد. چون هر چه تعداد ارقام بیشتر باشد تعداد و شماره تلفنهای خیلی بیشتری میتوان به مقتضیان واگذار کرد.
مثال 8: با اعداد 2 و 5 و 6 و 7 چند عدد:
الف) سه رقمی میتوان نوشت؟
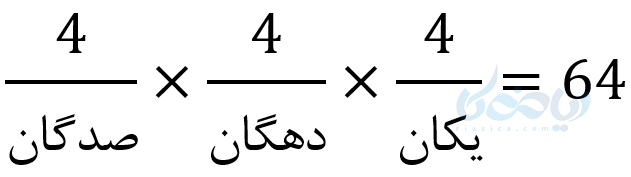
ب) سه رقمی بدون تکرار ارقام میتوان نوشت؟
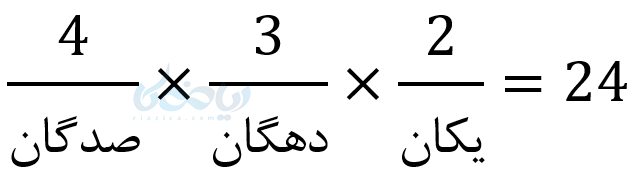
ج) سه رقمی زوج بدون تکرار ارقام میتوان نوشت؟
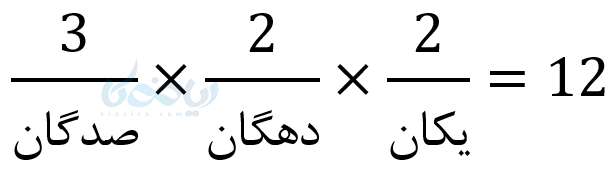
د) سه رقمی بزرگتر از 500 میتوان نوشت؟ (بدون تکرار ارقام)
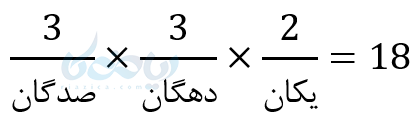
توضیح قسمت ج) چون میخواهیم عدد زوج بنویسیم پس برای یکان 2 انتخاب داریم (2 یا 6). حال میرویم سراغ صدگان چون یک عدد برای یکان در نظر گرفتهایم. پس برای صدگان 3 انتخاب و برای دهگان 2 انتخاب خواهیم داشت. چون هدف این سوال نوشتن اعداد بدون تکرار است، پس در هر مرحله عددی که در مرحله قبل انتخاب کردهایم کنار گذاشته میشود.
توضیح قسمت د) برای صدگان از یکی از سه عدد میتوانیم استفاده کنیم. حال اگر یکی از اینها انتخاب شود برای دهگان 3 انتخاب و برای یکان 2 انتخاب خواهیم داشت.
نکته ۲: وقتی در مسئلهای محدودیتی برای انتخابی داریم ابتدا تعداد حالتهای آن را در نظر میگیریم. سپس تعداد انتخابهای بقیه جایگاه را مینویسیم.
مثال 9: با ارقام 7 و 3 و 2 و 0 و بدون تکرار ارقام:
الف) چند عدد سه رقمی میتوان نوشت؟
چون صفر در صدگان نمیتواند قرار بگیرد، پس برای انتخاب صدگان 3 انتخاب داریم. (7 یا 2 یا 3)
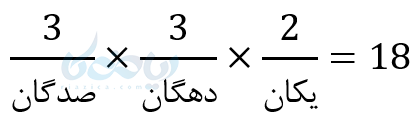
ب) چند عدد سه رقمی فرد میتوان نوشت؟
ابتدا فرد بودن عدد را در نظر میگیریم. پس به سراغ یکان میرویم. برای یکان دو انتخاب داریم، (3 یا 7). حال به سراغ صدگان میرویم. چون صفر را نمیتوانیم انتخاب کنیم. 3 یا 7 را هم قبلاً انتخاب کردهایم. پس برای صدگان نیز دو انتخاب داریم. یک عدد برای یکان و یکی برای صدگان انتخاب کردیم. پس دو انتخاب باقی مانده برای دهگان. در نهایت داریم:
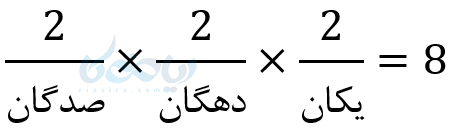
ج) چند عدد سه رقمی زوج میتوان نوشت؟
راه اول:
چون صفر جزء اعداد زوج است و اگر یکسان باشد یک حالت و اگر در یکان نباشد یک حالت دیگر به وجود میآید.
چون صفر جزء اعدا زوج است و از طرفی در صدگان نمیتواند قرار گیرد و دو حالت به وجود میآید.
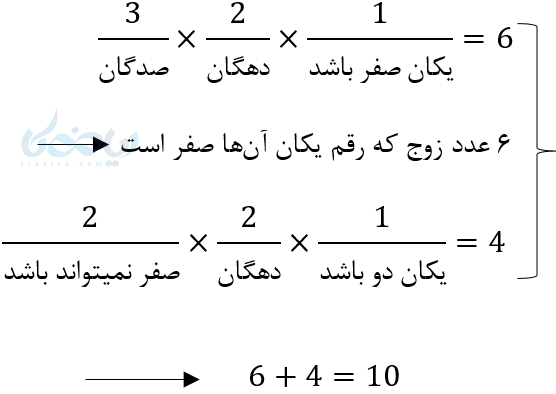
راه دوم: تعداد کل اعداد را از اعداد فرد کم کنیم:
\( \LARGE 18-8=10 \)
در مسائل مربوط به اصل شمارش، بدون شمردن باید هر مسئله را خوب تجزیه و تحلیل کنیم و با دقت جواب دهیم برای همین به این بخش آنالیز ترکیبی هم میگویند آنالیز یعنی تجزیه و تحلیل یعنی هر مسئله باید خوب تجزیه و تحلیل شود و همه جوانب آن در نظر گرفته شود.
زنگ آخر کلاس اصل شمارش بدون شمردن
در این بخش با هم موضوع اصل شمارش یاد گرفتیم. بخشهای ترکیب و جایگشت را در پستهای دیگر در آموزش ریاضی دهم یادمیگیریم. در صورتیکه هر سوالی از این نوشتار آموزشی داشتید، زیر همین بخش در دیدگاهها برای ما بنویسید. کارشناسان ریاضیکا حتما به سوالهایتان پاسخ میدهند. موفق باشید 🙂





?بسیار عالی بود
با سلام وعرض ادب
ممنون از لطف شما دوست عزیز
خیلی ممنون عالی بود
با سلام وعرض ادب
خوشحالیم که مفید بوده میتونید براییادگیری کامل پایه دهم از پکیج ویدیویی ما هم استفاده کنید
سلام ازکجا متوجه بشیم که باید ضرب انجام بدیم یاجمع ممنون میشم اگه جواب بدید
با سلام وادب
در همین پست کامل توضیح دادیم
سلام اگ بخواهیم رو صفحه شطرنج انتخاب هایی را داشته باشیم .(حرکت دو رخ بدون تهدید) و رنگ کردن یک جدول با رنگ های متمایز یا غیر متمایز چکار کنیم
سلام عالی یود
با سلام ممنون از نگاه شما
سلام و ممنون از مطالب خوب تان چگونه بفهمیم اصل شمارش است یا جایگشت و ترکیب؟متشکرم
سلام و ممنون از مطالب خوب تان چگونه بفهمیم اصل شمارش است یا جایگشت و ترکیب؟متشکرم
سلام ببخشید میشه مثال 7 رو بیشتر توضیح بدید
و اینکه چرا رفم اول 7 حالت و رقم دوم 1 حالت هست؟
سلام در حل توضیح داده شده به نکته آخر سوال دقت کنید