آموزش ریاضی پایه هشتم
ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
تصور کنید یه نفر فقط زبان ریاضی بلده، چطور باید باهاش حرف بزنیم؟ خب معلومه! با عبارتهای جبری. اگه کلاس درس ما یه فیلم سینمایی باشه، اون وقت عبارتهای جبری میشه زیرنویس ریاضی اون فیلم! در درس ساده کردن عبارت های جبری از مجموعه آموزش ریاضی پایه هشتم ، ابتدا مروری بر مفهوم عبارتهای جبری مانند جملات متشابه، الگوهای عددی و روش ضرب عبارتهای جبری خواهیم داشت و سپس به یادگیری ساده کردن عبارت های جبری خواهیم رسید.
یادآوری عبارتهای جبری
ما قبلاً در درسنامه عبارت های جبری با عبارت های جبری آشنا شدهایم. در پایههای بالاتر نیز با آنها سر و کار داریم؛ مانند تجزیه عبارتهای جبری پایه دهم. برای این که لازم نباشد برگردیم و کتاب سال قبل را باز کنیم، در این بخش مروری بر تعاریف مربوط به عبارت های جبری خواهیم داشت تا در ادامه بتوانیم سراغ ساده کردن عبارت های جبری برویم:
بیان عبارتهای جبری بصورت کلامی و بالعکس
فرض کنید دوست ما با فاصله از ما ایستاده و از ما میخواهد عبارتهای جبری داخل دفتر را برایش بخوانیم. اینجاست که عبارتهای جبری که با اعداد و حروف نوشته شده را بصورت کلامی بازگو میکنیم. به چند مثال زیر توجه کنید:
| عبارت های جبری | عبارت های کلامی |
|---|---|
| \( \Large a^0 = 1 (a \ne 0) \) | هر عددی (بجز صفر) به توان صفر،
برابر یک میشود. |
| \( \Large a^3 = a×a×a \) | مکعب هر عدد از سه بار ضرب عدد
درخودش بدست میآید. |
| \( \Large a^m × a^n = a^{(m+n)} \) | در ضرب دو عبارت توان دار با پایه های
مساوی،یک پایه را می نویسیم و توان ها را با هم جمع می کنیم. |
| \( \Large c^2 = a^2 + b^2 \) | رابطه فیثاغورس: مجذور وتر مثلث قائمالزاویه
برابر است با مجموع مجذورهای دو ضلع قائمه. |
| \( \Large a^1 = a \) | هر عدد به توان یک برابر خود آن عدد میشود. |
الگوهای عددی و عبارتهای جبری متناظر آنها
حتماً تا به حال با تعدادی عدد مواجه شدهاید که با نظم مشخصی در کنار یکدیگر قرار گرفتهاند؛ این نظم مشخص میتواند به عنوان مثال، فاصله مشخص بین یک عدد تا عدد بعدی (مانند فاصله 4 تایی اعداد در مثال زیر) باشد. مجموعه اعداد زوج و فرد دیگر نمونهها هستند.
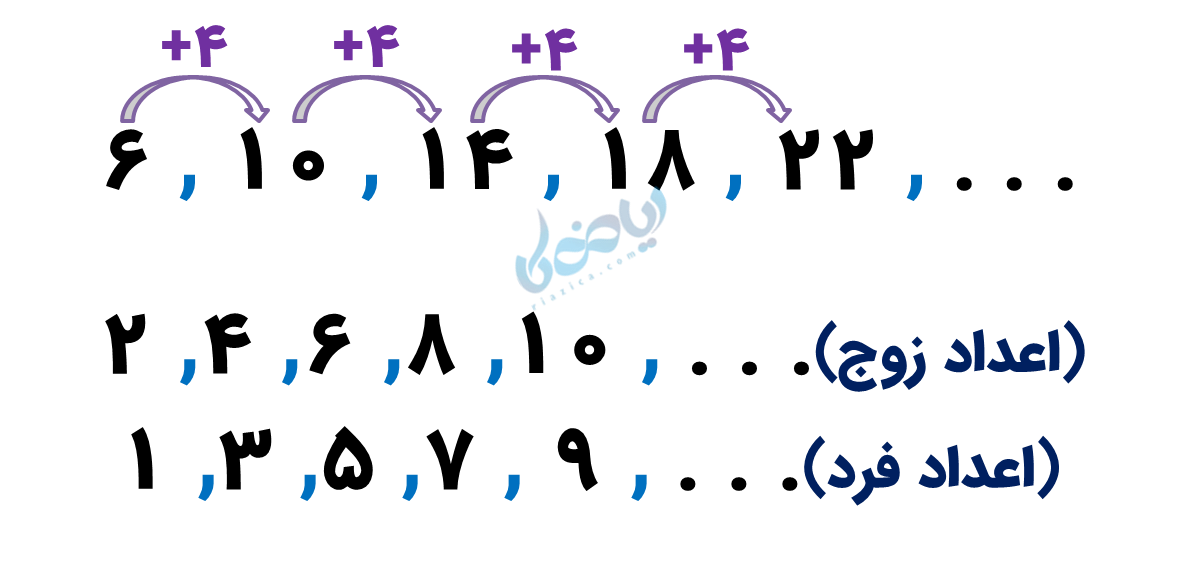
برای نشان دادن الگوهای عددی که به صورت کلی این نظم را نشان دهند، از عبارتهای جبری استفاده میشود.
مثال 1: عبارت جبری جملۀ \( \Large n \)اُم الگوهای عددی زیر را بنویسید.
. . . ، 9 ، 7 ، 5 ، 3 ، 1 (الف
. . . ، 81 ، 27 ، 9 ، 3 ، 1 (ب
حل 1:
الف) این الگو، اعداد فرد را نشان میدهد. میبینیم که این اعداد دو تا دو تا اضافه میشوند، پس باید ضریب 2 داشته باشند؛ یعنی \( \Large 2n \)! خب، اگر عبارت جبری آن \( \Large 2n \) باشد، ترتیب اعداد چگونه خواهد بود؟ \( \Large n \) از 1 شروع میشود:
. . . ، 10 ، 8 ، 6 ، 4 ، 2
با صورت سؤال مقایسه کنید! این الگو، یک واحد بیشتر از الگوی (الف) است؛ پس باید یک واحد از عبارت جبری کم کنیم، یعنی جملۀ \( \Large n \)اُم این الگوی عددی، \( \Large 2n-1 \) است:
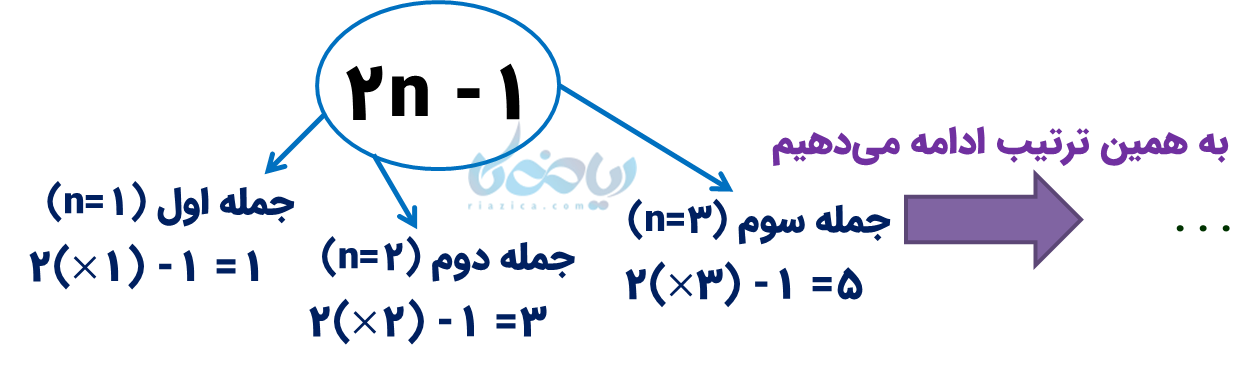
ب) به این الگو دقت کنید! هر عدد 3 برابر عدد قبلی شده است؛ (این یعنی توان 3). توجه کنید که هر عدد به توان صفر برابر است با 1، پس عدد اول توان صفرم 3 است:
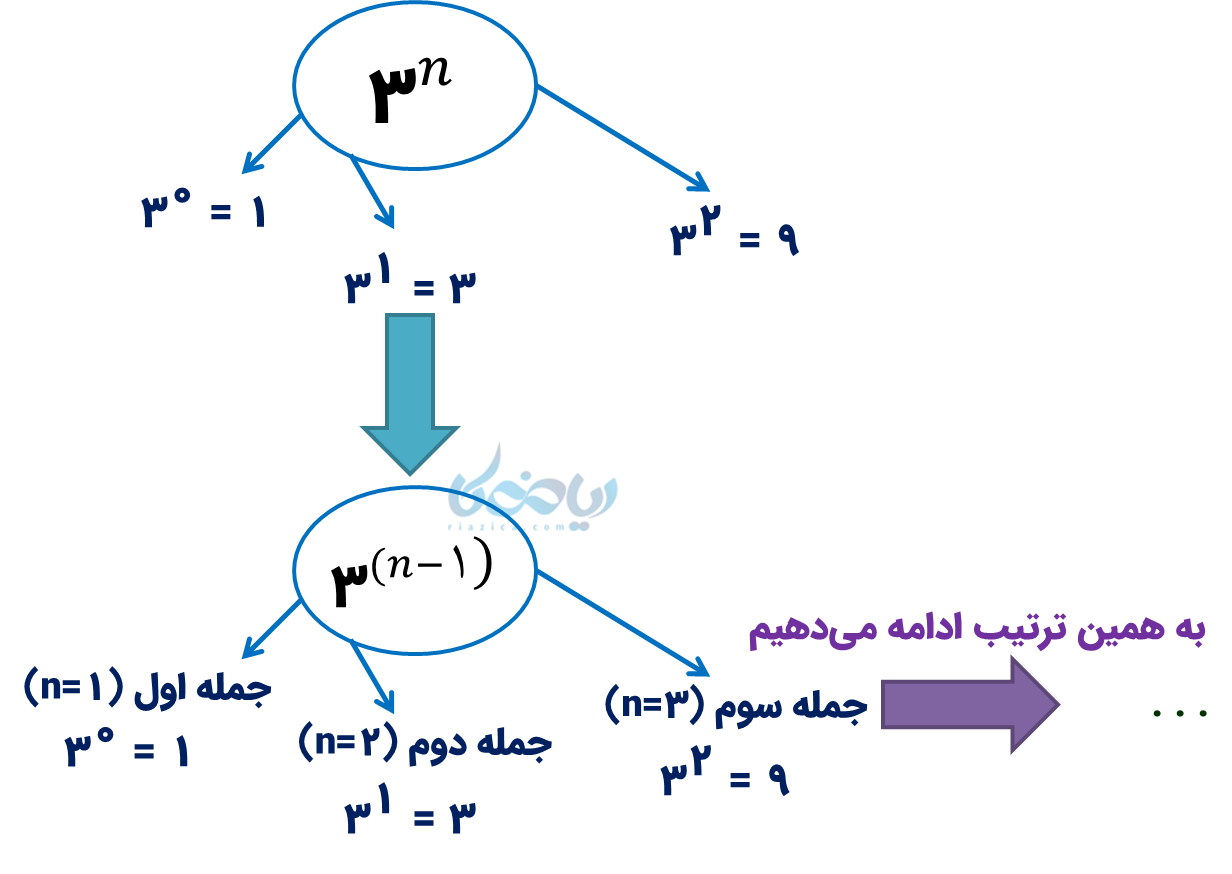
برای این که بتوانیم همه جملهها را با عبارت جبری ایجاد کنیم، یک واحد از توان کم کردیم. پس جملۀ \( \Large n \)اُم این الگوی عددی، \( \Large 3^{(n-1)} \) خواهد بود.
تعریف چندجملهایها
فراموش نکنید! در این درس قرار است به ساده کردن عبارت های جبری برسیم؛ اما قبل از آن داریم هر آنچه برای این کار لازم است به صورت مقدمه یاد میگیریم.
یکجملهایها
یکجملهایها، عبارتهای جبری هستند که از دو قسمت ضریب (عدد قبل از حروف انگلیسی) و متغیرها (حروف انگلیسی) تشکیل شدهاند، مانند:
\( \Large 19x^2y \) ، \( \Large \frac {1}{2} x \)
البته این، تعریف سادهای از یکجملهایها است که در سطح ریاضی پایه هشتم ارائه شده است. تعریف دقیقتر یکجملهایها را میتوانید در درس تابع چندجملهای به زبان ساده از ریاضی پایه دهم مشاهده کنید.
چندجملهایها
اگر بین عبارتهای جبری، علامت جمع یا تفریق قرار داشته باشد به آنها چند جملهای گفته میشود. در واقع چندجملهای، از تعدادی یکجملهای تشکیل شده است؛ به عنوان نمونه:
(دوجملهای) \( \Large -4xy + 2m^2n^3y^18 \)
(سهجملهای) \( \Large 2ab^2 – \frac {4}{3} y + 5 \)
جملههای متشابه ( شاه کلید ساده کردن عبارت های جبری )
جملات متشابه، جملهها (عبارت های جبری) هستند که همه قسمتهای حرفی آنها (متغیرها) و توانهای(درجه) آنها یکسان باشد. به عنوان نمونه، عبارتهای زیر در هر خط با هم متشابهاند:
\( \Large \frac {3}{4} x^2y \) و \( \Large -5x^2y \)
\( \Large x \) و \( \Large 4x \)
\( \Large -208axyb^2 \) و \( \Large 3axyb^2 \)
توجه: جملاتی که متغیرهای شبیه هم دارند ولی توان آنها متفاوت است متشابه نیستند؛ مانند دو جمله زیر که غیرمتشابهاند:
\( \Large 2x^2y^3 \) و \( \Large 2x^3y^2 \)
مثال 2: جملات متشابه را پیدا کرده و مشخص نمایید.
\( \Large 26x^3y^2 \)
\( \Large 26xyz \)
\( \Large -2x^3y^2 \)
\( \Large -2yzx \)
حل 2:
- دو جمله اول ضریب 26 و دو جمله دوم ضریب (2-) دارند، پس متشابهاند؟؟؟ خیر! دقت کنید که گفته شد حروف (یعنی متغیرها) باید مشابه باشند.
مشاهده میشود که عبارتهای جبری اول و سوم یعنی \( \Large 26x^3y^2 \) و \( \Large -2x^3y^2 \) دارای حروف همانند هستند، پس جملات متشابه خواهند بود.
امّا به جملات \( \Large 26xyz \) و \( \Large -2yzx \) دقت کنید! ظاهراً شبیه نیستند، ولی میدانیم که \( \Large xyz \) با \( \Large yzx \) تفاوتی ندارد؛ چون سه ضریب در هم ضرب شده و میدانیم عوض شدن جای اعداد در ضرب، تغییری در حاصلضرب ایجاد نمیکند. پس این دو جمله نیز متشابه هستند.
ضرب عبارتهای جبری
ضرب عبارتهای جبری هم برای ساده کردن عبارت های جبری گاهی لازم میشود؛ بعداً در مثال 4 خواهید دید که چند عبارت در هم ضرب شده و سپس از ما خواسته شده که ساده شده آنها را بنویسیم.
ضرب یکجملهای در یکجملهای
ضرایب در هم و متغیرها در هم ضرب میشوند؛ مثلاً:
\( \Large (-6yx) × (2x^2) = -12yx^3 \)
نکته: در ضرب عبارتهای جبری، اگر متغیرهایی که در هم ضرب میشوند یکسان باشند، یکی از پایهها را نوشته و توانها را با هم جمع میکنیم. (طبق روش گفته شده در درس خواص ضرب و تقسیم اعداد تواندار)
ضرب یکجملهای در چندجملهای
یکجملهای در تمام جملات چندجملهای ضرب میشود؛ به عنوان نمونه در ضرب زیر، یکجملهای ابتدا در عبارت اول و سپس در عبارت دوم ضرب شده و حاصلضرب این دو با هم جمع شده است:

ضرب چندجملهای در چندجملهای
تکتک جملات چندجملهای اول در تمام جملات چندجملهای دوم ضرب میشود (به این ویژگی، خاصیت توزیعپذیری گفته میشود). به عنوان مثال:
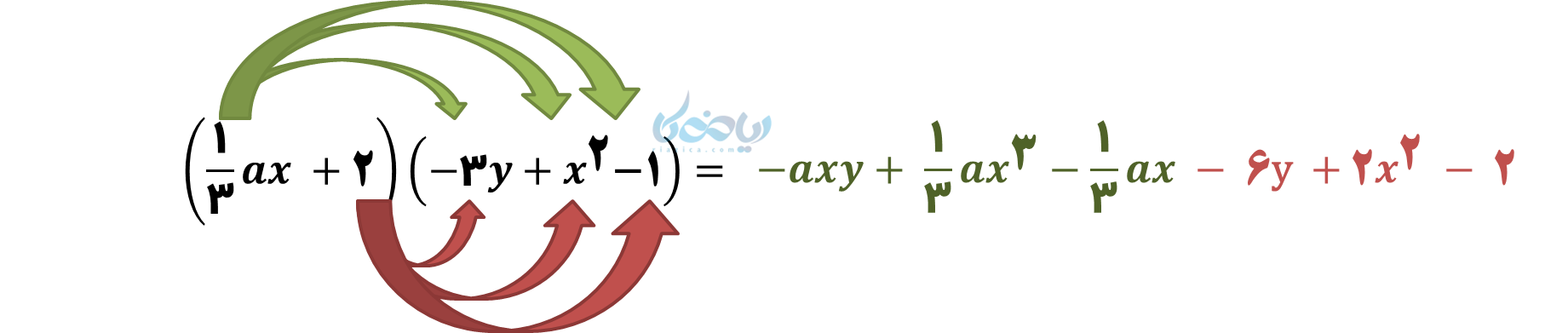
توجه: ضرب و تقسیم اعداد تواندار، قوانینی دارد که میتوانید در درسنامه ضرب و تقسیم اعداد تواندار مطالعه نمایید.
مثال 3: به کمک عبارتهای جبری تساوی مساحتهای شکل زیر را نشان دهید.
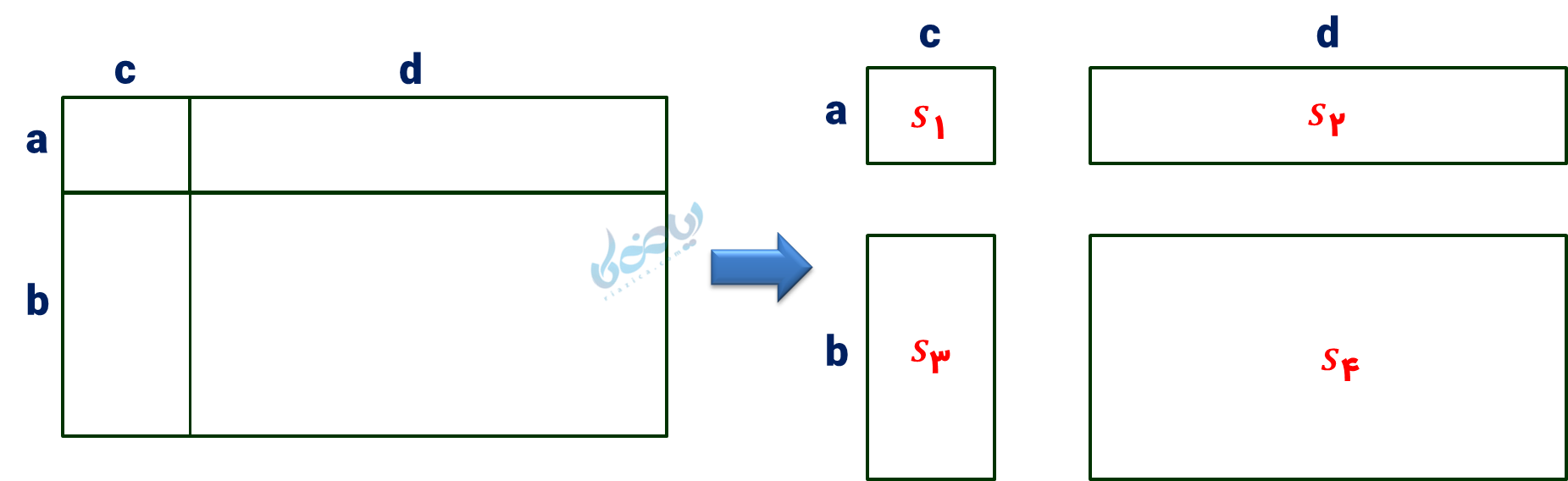
حل 3:
مساحت شکل سمت چپ برابر است با مجموع مساحتهای شکل سمت راست؛ مساحت مستطیلهای کوچک را از \( \Large S_1 \) تا \( \Large S_4 \) نامگذاری کردهایم.
مساحت کل را \( \Large S \) نامیده و با استفاده از ضرب چندجملهای آن را بدست میآوریم:
\( \Large S = (a+b) × (c+d) \)
\( \Large S = ac + ad + bc + bd \)
حال مساحتهای \( \Large S_1 \) تا \( \Large S_4 \) را بدست آورده و با هم جمع میکنیم:
\( \Large S_1 + S_2 + S_3 + S_4 \)
\( \Large = ac + ad + bc + bd \)
با مقایسه این دو عبارت، اکنون میتوانیم تساوی مساحتهای سمت چپ و راست را بدین صورت نوشت:
\( \Large S = S_1 + S_2 + S_3 + S_4 \)
ساده کردن عبارت های جبری
برای ساده کردن عبارت های جبری مراحل زیر را طی میکنیم:
- جملات متشابه را مشخص میکنیم؛
- ضرایب جملات متشابه را با هم جمع میکنیم؛
- جملات غیرمتشابه را بدون تغییر مینویسیم.
مثال 4: عبارتهای جبری زیر را ساده کنید.
\( \Large (2x-y)^2 \) (الف
\( \Large \frac{1}{2} x (4y-6x) + 3y – 2xy \) (ب
حل 4:
الف) عبارت درون پرانتز کلاً به توان دو رسیده است؛ پس میتوان این عبارت را دو بار در خودش ضرب کرد، یعنی:
\( \Large (2x-y) × (2x-y) \)
حال همه جملات دوجملهای اول را در همه جملات چندجملهای دوم ضرب میکنیم:
\( \Large = 4x^2 – 2xy – 2xy + y^2 \)
برای ساده کردن عبارت های جبری ، جملات متشابه را پیدا کنیم: \( \Large – 2xy \)و \( \Large – 2xy \) متشابه و بقیه جملات، غیرمتشابهاند. پس این دو را با هم جمع میکنیم و بقیه را بی تغییر مینویسیم:
\( \Large = 4x^2 – 4xy + y^2 \)
ب) ابتدا یکجملهای \( \Large \frac {1}{2} x \) را در پرانتز بعد از آن (دوجملهای) ضرب میکنیم و بقیه عبارتها را هم مینویسیم:
\( \Large 2xy – 3x^2+ 3y – 2xy \)
عبارتهای \( \Large 2xy \) و \( \Large -2xy \) متشابه هستند، پس آنها را با هم جمع میکنیم؛ حاصل صفر خواهد شد. با اضافه کردن جملات غیرمتشابه نهایتاً خواهیم داشت:
\( \LARGE = – 3x^2+ 3y \)
توصیه می شود قبل از خواندن ین پست درسنامه های عبارت های جبری و ساده کردن عبارت های جبری ومعادله ریاضی هفتم را مطالعه کنید.
ویدیو از عبارت های جبری هشتم
در این ویدیو عبارت های جبری هشتم به طور کامل با مثال های فراوان تدریس شده است
زنگ آخر کلاس ساده کردن عبارت های جبری
در این درسنامه از فصل جبر و معادله ریاضی هشتم، ابتدا یادآوری مختصری از عبارتهای جبری داشتیم و الگوهای عددی، تعریف چندجملهای، جملات متشابه و نحوه ضرب چندجملهای ها در هم را مرور کردیم. سپس با سه مرحله و به کمک جملات متشابه به ساده کردن عبارت های جبری پرداختیم. در واقع ساده کردن عبارت های جبری به ما کمک میکند به جای تعداد زیادی جمله، معادل آن را با چند عبارت کوتاه بنویسیم.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاهها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی هشتم به شما پیشنهاد میدهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!





خیلی عالی بود دستتون درد نکنه????
سلام. خواهش میکنم.
سلام من هفته آینده بای توی کلاس معلم راهنمام همین مبحث رو تدریس کنم ؛ کارورز هستم…از روش تدریستون خیلی خوشم اومد و میخوام همین روند رو برای تدریس انجام بدم . مرسی ازتون 🙂
با سلام وادب
خوشحالیم که تدریس ما برای شما مفید واقع شده میتونید با تهیه پکیج ویدیویی پایه هشتم در تدریستون در سالهای آینده استفاده کنید
س باشه ما چکار کنیم در درس ریاضی خوب باشیم
سلام دوست عزیز
دو کار باید انجام بدی یکی اینکه باور کنی میتونی ریاضی رو بیاموزی و دوم تمرین وتمرین وتمرین
مرسی واقعا لطف کردین
سلام عرض ادب
خیلی ممنون از پیام پر مهرتون.
موفق باشید.
ساده شده عبارات زیر چه می شود؟
?=7xy_x²_3yx+2x²_1
?=(X+3)(x_3)
یا سلام ووقتبه خیر
دوست عزیز جواب این سوالات خیلی ساده هست اگه پست رو خوب بخونید جواب رو میتونید بنویسید
عبارت جبری 12x+15y+17x+yساده کنید
سلام
16y+29x
موفق باشید.
پاسخ a+b)³)چه میشود؟
سلام و عرض ادب
a+b) 3 = a 3 + 3a2b + 3ab2 + b3)
موفق باشید.
عالی گفتید ممنون
سلام
ممنون ازاینکه با انرژیاتون ما را در ادامه راه حمایت می کنید.
موفق باشید.
میشه عبارت جبری رو به صورت ساده توضیح بدید؟
سلام و وقت به خیر
ما در دوره ابتدایی به جای مجهول های از جای خالی استفاده می کردیم مثلا مربع، دایره و غیره. اما بخاطر راحتی و سهولت کار به جای جای خالی از حروف انگلیسی استفاده می کنیم مثل x,y,.. ، که به هرکدام یک جمله جبری می گویند شرط جمع و تفریق عبارت های جبری متشابه بودن آن ها است. یعنی متغیرها یکی باشند، در اینصورت ضریب های آن ها یعنی عددهای کنار متغیر را با هم جمع و تفریق می کنیم.
موفق باشید.
سلام چطور باید بفهمم ایکس چه مقدار توان دارد
سلام و عرض ادب
عدد بالای متغیر توان است اگر هیچی نداشت برابر با ۱ است.
موفق باشید.
عاااااالی توضیح دادید..واقعا ممنونم??
سلام و عرض ادب
ممنون از توجهتون.
موفق باشید.
سلام مجذور یعنی چی
سلام عرض ادب
یعنی توان دوم هر عدد را مجذور آن عدد می گویند.
موفق باشید.
سلام عالی خیلی خوب توضیح دادید دست گلتون درد نکن?????????????این هم تشویق برای شما لطفا ولی بهم جواب بدید????
سلام و عرض ادب
متشکرم از توجهی که داشتید.
موفق باشبد.
عبارت جبری زیر را ساده کنید
(۴x²+2x+1)(2x_1) _8x³
سلام دوست عزیز
جواب یک میشود
سلام خیلی عالی من از این توضیح خوشم اومد خیلی عالی و این تشویق برای شما و دست گلتون درد نکنه????????????????
سلام دوست عزیز
ممنون از انرژی که دادید.
موفق باشید.
عبارت جبری زیر را ساده کنید.
لطفا توضیح هم بدهید ممنون.
(۴x²+2x+1)(2x_1)_8x³
سلام چون جواب پرانتز میشود 8x^3-1 که در منفی ضرب میشود ودوجمله قرینه با م ساده میشود و1 باقی می ماند
عالی بود دستتون درد نکنه
با سلام به شما دوست عزیز
ممنون از توجه ولطف شما
اشتراکها: امیر محمد حسینی
با سلام وعرض ادب
خدا رو شکر که براتون مفید بوده
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام. لطفا جواب این رو بهم بگید، ممنونتون میشم:
رادیکال ۵۰ به اضافه رادیکال ۹۸ منهای ۸=
خیلی ممنون و مرسی?
با سلام
رادیکال ۵۰ میشه ۵رادیکال ۲ورادیکال ۹۸ میشه ۷رادیکال ۲و رادیکال ۸ میشه ۲رادیکال ۲ پس حاصل نهایی میشه ۱۰ رادیکال ۲
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام مرسی بابت توضیحت ☆
جواب این عبارت چی میشه؟!
(4X–7)(۸X+9)
با سلام واحترام
32x^2-20x-63
این عبارت و ساده کنید
3n+2b+4n_5b
سلامد وست عزیز
پست رو نوشتیم تا عبارتی به این سادگی رو خودتون ساده کنید
مرسی برای توضیحات تان میشه لطفاً بگید حاصل این عبارت چی میشه ؟ ??
−4 ?? + 2 ?(? + 3 ?) + 5?
2 =
سلام گفته عبارت جبری را ساده کنید a+5 b_10)3_)
با سلام وعرض ادب
این عبارتی که شما نوشتید ساده نمیشه
چگونه a_b a_bداخل پرانتز رو ساده بدست بیاریم
با سلام واحترام صورتسوال مشخص نیست که بین دو تا a,b چه علامتی هست
سلام ممنونم بابت اطلاعات عالیتون ??????????????????
با سلام و عرض ادب
خواهش میکنم دوست عزیز میتونید با تهیه پکیج ویدیویی پایه هشتم از آموزشهای ما استفاده کنید
سلام
خیلی عالی و کاملا مختصر و مفید بود???
با سلاموادب
ممنون از نظر لطف شما وحدت رو شکر که مفید بوده
سلام عالی بود فقط آیا میتوان در ساده کردن جملات جملات را در هم ضرب کرد
با سلام وادب
بله بهتره عبارتهای داخل پرانتز اگه ساده میشن ساده کنیم وبعد ضرب کنیم و بعد اگهبازم ساده میشن ساده کنیم
آقا دمتون گرم خیلی عالی بود
لطفا مباحث دیگه رو هم به همین سادگی توضیح بدید.تشکر
با سلام وادب
دوست عزیز ممنون از لطف شما ما تمام مباحث پایه هشتم رو به همین ترتیب نوشتیم ودر سایت قرار دادیم تدریس ویدیویی هم داریم
سلام لطفاً این عبارت رو ساده کنید
3ab+4a²_5ab+2a²
با سلام
2ab+6a^2-
سلام خسته نباشید میشه درباره ساده کردن کسر های جبری هم توضیح دهید؟
با سلام در پستهای دیگه گفتیم
سلام میشه توضیح بدید تو عبارت هایی که 3 تا پرانتز دارن چیکار باید بکنیم؟
مثلا (z
با سلام وادب
ابتدا اگه بین اونها جمع وتفریق هست پرانتز ها رو برمیداریم فقط اگه پشت پرانتز منفی باشه داخل پارنتزضرب میکنیم
سلام وقت بخیر جواب این سوال چیه 5a-3b+a+b+5
دوست عزیز اینکه خیلی ساده هست پست رو بخون جواب بده حتما میتونی باور کن
عالی و مفید
سلام در عبارت پایینی منفی پشت پرانتز در هر دو عبارتِ داخلش ضرب میشه؟
(۲³_۳²)_۴
با سلام بله در هردو ضرب میشه