آموزش ریاضی پایه هشتم
زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
به کشور چندضلعیها خوش آمدید! قبول دارید اگر یک کشور به تولید داخل و نیروهای بومی خود اهمیت دهد، قطعاً موفق خواهد شد؟ خیالتان راحت… این درس مطالعات اجتماعی نیست. بازی و ریاضی چند ضلعی هاست که زاویه های داخلی در آن بسیار اهمیت دارند. فراموش نکنید، در مثالهای این درس شما رئیسجمهور این کشور خواهید بود.
در این درسنامه از مجموعه آموزش ریاضی پایه هشتم ، با زاویه های داخلی آشنا خواهید شد. با یادگیری مجموع زوایای داخلی یک چند ضلعی، اندازه زاویه داخلی یک چند ضلعی منتظم و حل چندین مثال متنوع از آنها آماده کاشیکاری خواهید بود. تعجب نکنید! تا پایان همراه ما باشید.
تعریف زاویه های داخلی
زاویههایی که درون یک چند ضلعی قرار دارند، زاویه های داخلی آن چند ضلعی گفته میشوند.
به عنوان نمونه در شش ضلعی زیر، زاویههایی که با رنگ سبز مشخص شدهاند، زاویه های داخلی آن هستند:
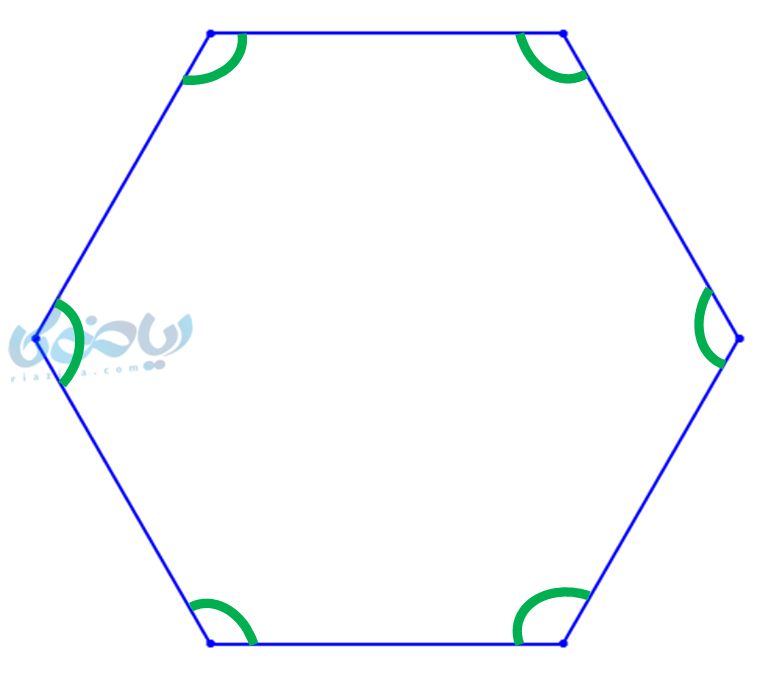
انواع زاویه در چند ضلعی ها
در این درس و درس زاویه های خارجی خواهیم دید که در چند ضلعی ها دو نوع زاویه وجود دارد:
- زاویه داخلی
- زاویه خارجی
برای این که تفاوت این دو نوع زاویه را کاملاً متوجه شوید، به زاویه های داخلی و خارجی نشان داده شده در شکل زیر توجه کنید؛ در این شکل بعضی از زاویه های داخلی با رنگ سبز و زاویه های خارجی آنها با رنگ قرمز نشان داده شده است:
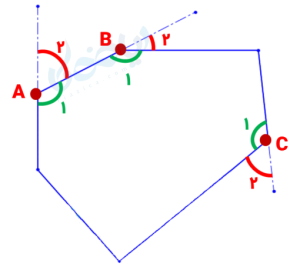
نکته: هر چندضلعی به تعداد اضلاعش دارای زاویه داخلی است؛ به عنوان مثال یک شش ضلعی، دارای ۶ زاویه داخلی است.
اندازه زاویه های داخلی در چند ضلعی ها
مجموع زاویه های داخلی یک چند ضلعی
مجموع زاویه های داخلی یک \( \Large n \)– ضلعی از رابطه زیر بدست میآید:
\( \Large (n-2) × 180° \)
در این رابطه \( \Large n \) تعداد اضلاع چند ضلعی را نشان میدهد.
مثال 1: در چندضلعی زیر، اندازۀ زاویه \( \Large \hat C \) را بدست آورید.
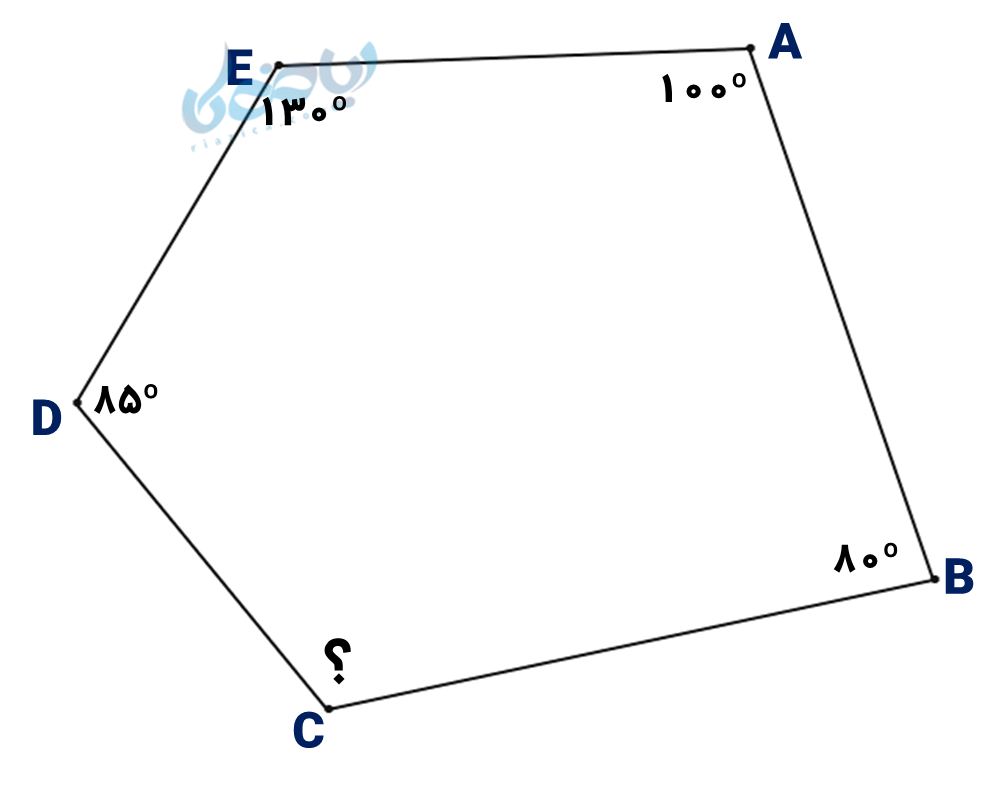
حل 1:
در صورت سؤال، یک پنجضلعی رسم شده است. با توجه به آنچه آموختیم، کافی است در رابطه بالا به جای \( \Large n \)، عدد 5 قرار دهیم. مجموع زوایای داخلی یک پنج ضلعی برابر خواهد بود با:
\( \Large (5-2) × 180° \)
\( \Large = 3 × 180° = 540° \)
اکنون که مجموع زاویه های داخلی را میدانیم، آنها را با هم جمع زده و برابر عدد بدست آمده قرار میدهیم:
\( \Large \hat A + \hat B + \hat C + \hat D + \hat E = 540° \)
\( \Large 100° + 80° + \hat C + 85° + 130° = 540° \)
\( \Large → \hat C + 395° = 540° \)
\( \Large → \hat C = 540° – 395° \)
\( \Large → \hat C = 540° – 395° = 145° \)
مجموع زاویه های داخلی مثلث
با توجه به رابطۀ گفته شده، مجموع زاویه های داخلی مثلث برابر با °180 است. (چرا؟) کافی است به جای \( \Large n \)، عدد 3 (تعداد اضلاع مثلث) قرار دهیم.
\( \Large (3-2) × 180° = 180° \)
مجموع زاویه های داخلی چهارضلعی
مجموع زوایای داخلی چهار ضلعی ها برابر با °360 است. (چرا؟) برای اثبات این موضوع میتوانیم به جای \( \Large n \)، عدد 4 قرار دهیم:
\( \Large (4-2) × 180° = 360° \)
همچنین برای اثبات این موضوع میتوانیم از روش زیر استفاده کنیم:
متوازی الاضلاع زیر را به عنوان نمونهای از چهار ضلعی ها در نظر بگیرید. با رسم خطچین مشکی رنگ، این چهار ضلعی تبدیل به دو مثلث \( \Large ABC \) و \( \Large ADC \) میشود.
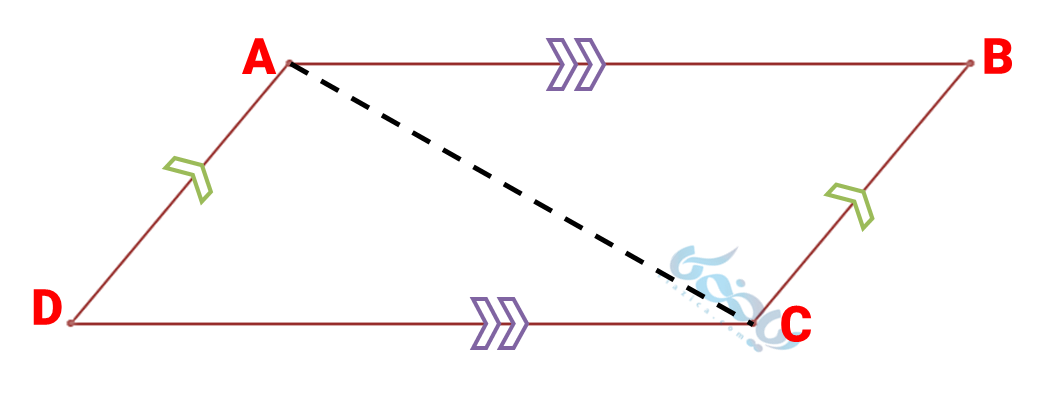
از آنجا که مجموع زاویه های داخلی مثلث °180 بوده و همچنین با توجه به این که چهار ضلعی از دو مثلث تشکیل شده است، مجموع زوایای داخلی چهار ضلعی دو برابر مثلث خواهد بود:
\( \Large 2 × 180° = 360° \)
مثال 2: مجموع زوایای داخلی یک چند ضلعی °1080 است. این چند ضلعی چند رأس دارد؟
حل 2:
برای حل این سؤال، باید فرمول مجموع زاویه های داخلی را نوشته و با حل معادله تعداد اضلاع را بدست آوریم:
\( \Large (n-2) × 180° = 1080° \)
\( \Large → (n-2) = \frac {1080}{180} = 6 \)
\( \Large → n = 6 + 2 = 8 \)
بنابراین این شکل، هشتضلعی است. (دقّت کنید!) در صورت سؤال گفته شده تعداد رأسها را بدست آورید؛ میدانیم هر چند ضلعی به تعداد اضلاعش دارای رأس است، بنابراین این چند ضلعی 8 رأس دارد.
زاویه های داخلی در چند ضلعی منتظم
اندازه زاویه داخلی یک چند ضلعی منتظم
اندازه هر زاویه داخلی یک \( \Large n \)– ضلعی منتظم از رابطه زیر بدست میآید:
\( \LARGE \frac {(n-2) × 180°}{n} \)
در این رابطه \( \Large n \) تعداد اضلاع چندضلعی را نشان میدهد.
اثبات: در درس خط تقارن آموختیم که در یک چندضلعی منتظم، زاویهها با هم و ضلعها با هم برابرند. بنابراین با توجه به رابطه بخش قبل برای مجموع زاویه های داخلی یک چندضلعی، کافی است مجموع زوایای داخلی را به تعداد زاویهها (\( \Large n \)) تقسیم کنیم.
مثال 3: هر یک از زاویه های داخلی چندضلعی زیر چند درجه است؟
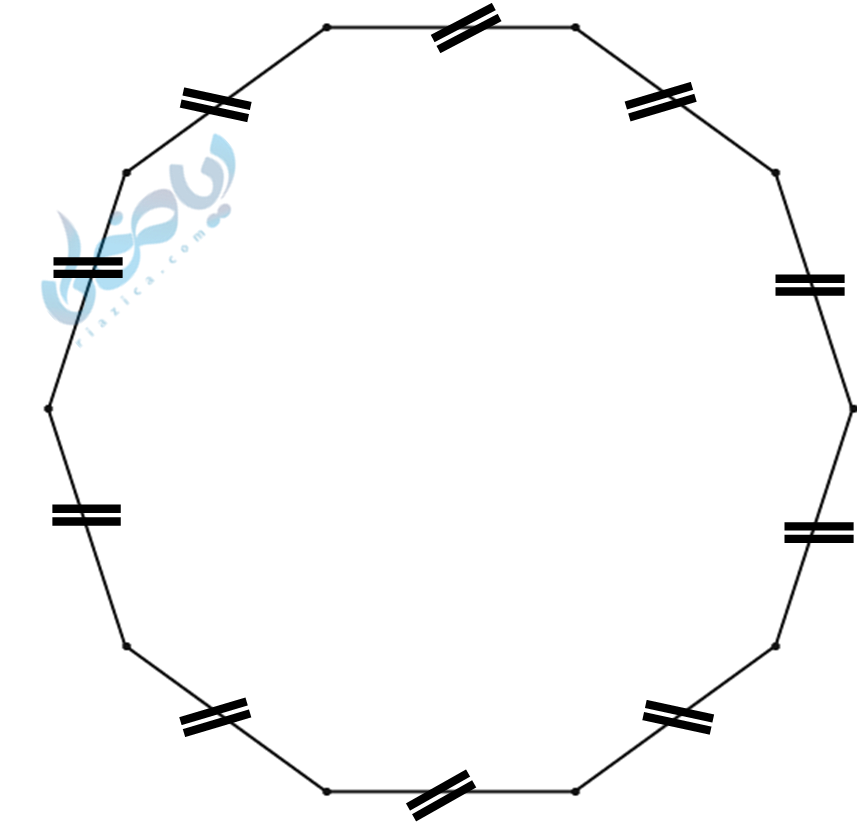
حل 3:
این چند ضلعی، یک ده ضلعی منتظم است. (چرا؟) چون همه اضلاع آن با هم برابرند. برای بدست آوردن هر یک از زوایای داخلی، از رابطه گفته شده برای چند ضلعی های منتظم استفاده کرده و به جای \( \Large n \)، عدد 10 قرار میدهیم:
\( \Large \frac {(10-2) × 180°}{10} \)
\( \Large = \frac {1440}{10} = 144° \)
مثال 4: شکل زیر یک طرح هنری خاتمکاری شده بصورت چندضلعی منتظم را نشان میدهد که بخشی از آن در اثر حادثهای از بین رفته است. از شما خواسته شده به کمک زاویه نشان داده شده تعداد اضلاع آن را بدست آورید.

حل 4:
اندازه یک زاویه چند ضلعی منتظم داده شده است؛ پس باید از رابطه بالا استفاده کرده و با حل معادله تعداد اضلاع را بدست آوریم:
\( \Large \frac {(n-2) × 180°}{n} = 120° \)
طرفین وسطین کرده و مخرج کسر سمت چپ (\( \Large n \)) را در صورت کسر سمت راست تساوی (120) ضرب میکنیم:
\( \Large (n-2) × 180 = 120n \)
در این مرحله با استفاده از ضرب عدد در چندجملهای سمت چپ تساوی را ساده میکنیم:
\( \Large → 180n – 360 = 120n \)
\( \Large → 180n – 120n = 360 \)
\( \Large → 60n = 360 \)
\( \Large → n = \frac {360}{60} = 6 \)
بنابراین طرح هنری داده شده، یک ششضلعی منتظم را نشان میدهد.
کاشیکاری با چند ضلعی های منتظم
یکی از شکلهایی که در کاشیکاری بسیار از آن استفاده میشود، چند ضلعی منتظم است. اگر بخواهیم در یک کاشیکاری فقط از یک نوع چند ضلعی منتظم استفاده کنیم، باید عدد 360 بر اندازه زاویه داخلی آن بخشپذیر باشد.
نکته: یک دور کامل (مانند یک دایره) برابر با °360 است.
مثال 5: با دلیل و رسم شکل نشان دهید کدامیک از چندضلعیهای زیر به تنهایی مناسب کاشیکاری است؟
الف) هشتضلعی منتظم ب) ششضلعی منتظم
حل 5:
مطابق نکته گفتهشده، ابتدا اندازه زاویه های داخلی هر شکل را بدست میآوریم:
\( \Large \frac {(8-2) × 180°}{8} \) (زاویه هشتضلعی منتظم)
\( \Large = \frac {1080°}{8} = 135° \)
\( \Large \frac {(6-2) × 180°}{6} \) (زاویه ششضلعی منتظم)
\( \Large = \frac {720°}{6} = 120° \)
حال بررسی میکنیم که عدد 360 بر کدامیک بخشپذیر است:
\( \Large = \frac {360}{135} \simeq 2/67 \)
\( \Large = \frac {360}{120} = 3 \)
بنابراین تنها با استفاده از هشت ضلعی منتظم نمیتوان کاشیکاری کرد. اما این کار با ششضلعی منتظم امکانپذیر است. این موضوع در شکل زیر نیز نشان داده شده است:
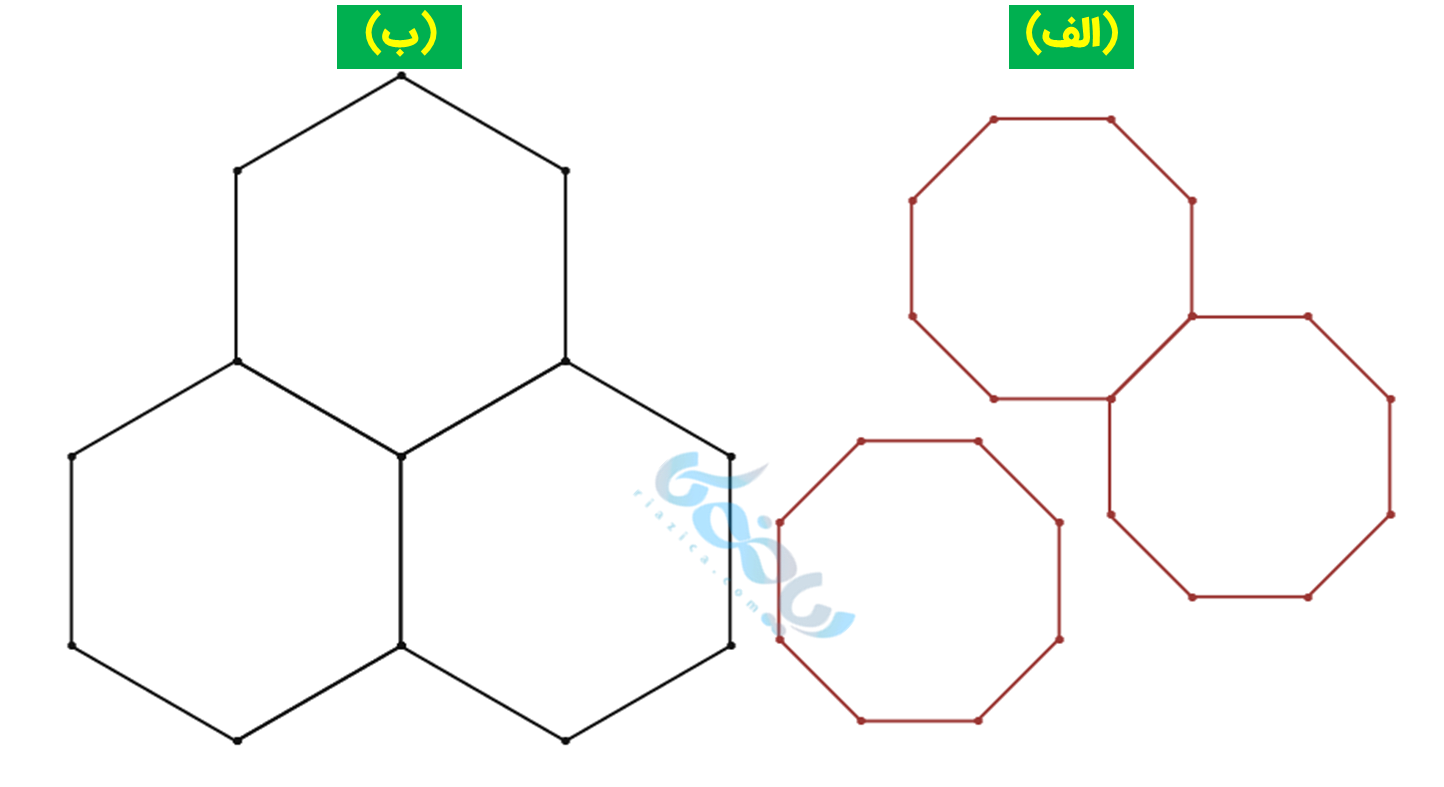
همانگونه که مشاهده میکنید دو هشت ضلعی در یک گوشه به هم متصل شدهاند، اما نمیتوانیم هشت ضلعی سوم را به آنها وصل کنیم تا آن گوشه را کامل کند.
از سوی دیگر، سه شش ضلعی به صورتی کنار هم قرار گرفتهاند که کاملاً فضا را پر میکنند.
در ادامه درسنامه زاویه های خارجی را نیز مطالعه کنید
ویدیو از زاویه های داخلی وخارجی چند ضلعی ها
در این ویدیو چندضلعیها وانواع آن وزاویه های داخلی وخارجی چند ضلعی ها توضیح داده شده ویک مثال عالی از این مبحث آورده شده
زنگ آخر کلاس زاویه های داخلی
ماجراجویی ما در کشور چند ضلعیها به پایان رسید! در این درس با زاویه های داخلی در چند ضلعیها و تفاوت آن با زاویه خارجی آشنا شدیم. اکنون میتوانیم مجموع زوایای داخلی در هر چند ضلعی و اندازه یک زاویه داخلی در چند ضلعی منتظم را با استفاده از رابطه ریاضی بدست آوریم. کاشیکاری با استفاده از چند ضلعی ها فوت کوزهگری این درس بود که در پایان درس با یک روش ساده یاد گرفتیم.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاهها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی هشتم به شما پیشنهاد میدهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!





عال
ممنون دوست عزیز
عالی بود مرسی
اصل مطلبو نگفتی
با سلام دوست عزیز
اصل مطلب چی هست؟
خدایی دمتون گرم عاااالی بود مرسیییی
خدایی دمتون گرم عاااالی بود مرسیییی ممنون که وقت میذارید
ممنون از شما و انرژی که میذارید
وقت بخیر
راه ارتباطی با شما رو میشه بدونم؟
با شماره 09128148975 تماس بگیرید
ان هایی که گفتند بد است اصلن نخوندن مطلب را