آموزش ریاضی پایه هفتم
ساده کردن عبارت های توان دار هفتم 🔤❎ – ۲ قانون مهم ضرب!
در درسنامهٔ ساده کردن عبارت های توان دار هفتم به بررسی دو مورد زیر میپردازیم:
- ضرب عبارتهای تواندار با پایههای مساوی
- ضرب عبارتهای تواندار با توانهای مساوی
سعی میکنیم با حل مثالهای مختلف، به درک بهتر شما از این مبحث کمک کنیم. با ما تا انتهای درسنامه همراه باشید.
ضرب عبارتهای تواندار با پایههای مساوی
ضرب عبارتهای تواندار با پایههای مساوی: اگر دو عبارت تواندار با پایههای مساوی را در یکدیگر ضرب کنیم، پایه تغییری نکرده و توانها با یکدیگر جمع میشوند. میتوان این قانون را به صورت زیر نمایش داد:
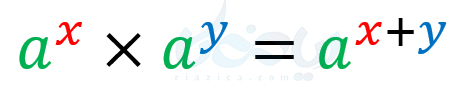
برای اینکه متوجه شوید چرا چنین اتفاقی میافتد، کافی است دو عدد با پایههای مساوی را در یکدیگر ضرب کنید. مثلاً، فرض کنید میخواهیم حاصل \(\Large 3^2 \times 3^4\) را به دست آوریم. با استفاده از تعریف توان میتوان نوشت:
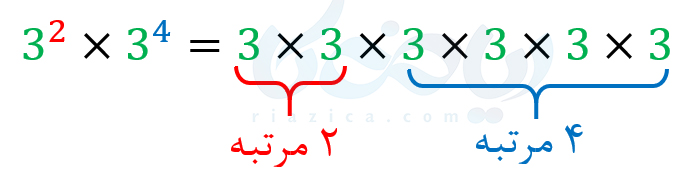
در واقع، با توجه به عبارت بالا، عدد \(\Large 3\) را به تعداد \(\Large 2+4\) بار در خودش ضرب کردهایم. پس میتوان نوشت:

مثال از درسنامهٔ ساده کردن عبارت های توان دار هفتم
مثال 1: حاصل عبارتهای \(\Large 4^5 \times 4^7\) و \(\Large 2^3 \times 2^2\) را به دست آورید.
حل: پایهها مساوی است، بنابراین کافی است توانها را با یکدیگر جمع کنیم:
\(\LARGE 4^5 \times 4^7=4^{5+7}=4^{11}\)
\(\LARGE 2^3 \times 2^2=2^{3+2}=2^5\)
مثال از درسنامهٔ ساده کردن عبارت های توان دار هفتم
مثال 2: حاصل عبارت \(\Large (-\frac{3}{5})^3 \times (-0.6)^5\) را به دست آورید.
حل: به ظاهر، پایهها متفاوت هستند، اما اگر دقت کنید، \(\Large -\frac{3}{5}\) با \(\Large -0.6\) برابر است. بنابراین کافی است توانها را با یکدیگر جمع کنیم:
\(\Large (-\frac{3}{5})^3 \times (-0.6)^5=(-0.6)^{3+5}\)
\(\Large \Rightarrow (-\frac{3}{5})^3 \times (-0.6)^5=(-0.6)^8\)
همان طور که در درسنامهٔ محاسبه عبارت توان دار خواندید، زمانی که عدد منفی به توان زوج میرسد، حاصل مثبت خواهد شد. بنابراین میتوانیم \(\LARGE (-0.6)^8\) را \(\LARGE 0.6^8\) بنویسیم.
مثال از درسنامهٔ ساده کردن عبارت های توان دار هفتم
مثال 3: اگر \(\Large a^b=80\) و \(\Large a^2=5\) باشد، \(\Large a^{b+2}\) را به دست آورید.
حل: نیازی به دانستن مقدار \(\Large a\) نیست. از آنجاییکه پایهها با یکدیگر برابر هستند، میتوانیم توانها را جمع کنیم:
\(\LARGE a^{b+2}=a^b \times a^2\)
\(\LARGE \Rightarrow a^{b+2}=80 \times 5=400\)
ضرب عبارتهای تواندار با توان مساوی
ضرب عبارتهای تواندار با توانهای مساوی: اگر دو عبارت تواندار با توانهای مساوی را در یکدیگر ضرب کنیم، توان تغییری نکرده و پایهها در یکدیگر ضرب میشوند. میتوان این قانون را به صورت زیر نمایش داد:

برای اینکه متوجه شوید چرا چنین اتفاقی میافتد، کافی است دو عدد با توانهای مساوی را در یکدیگر ضرب کنید. مثلاً، فرض کنید میخواهیم حاصل \(\Large 4^2 \times 3^2\) را به دست آوریم. با استفاده از تعریف توان میتوان نوشت:

در واقع، با توجه به عبارت بالا، عدد \(\Large 4 \times 3\) را \(\Large 2\) بار در خودش ضرب کردهایم. پس میتوان نوشت:

دو حالت خاص
ممکن است در برخی از مسائل با یکی از دو حالت زیر روبهرو شوید:
- ضرب عبارتهایی که هم پایه و هم توان یکسان دارند.
- ضرب عبارتهایی که نه پایهٔ یکسان و نه توان یکسان دارند.
در حالت اول، از هر کدام از دو روشی که گفتیم میتوانید استفاده کنید؛ یعنی یا پایه را ثابت در نظر گرفته و توانها را با یکدیگر جمع کنید، یا توان را ثابت در نظر گرفته و پایهها را در یکدیگر ضرب کنید. در حالت دوم نیز، امکان سادهسازی وجود ندارد. تنها اگر عبارت عددی داشته باشید، میتوانید مقدار عددی عبارت تواندار را محاسبه کنید.
مثال از درسنامهٔ ساده کردن عبارت های توان دار هفتم
مثال 4: حاصل عبارتهای \(\Large 2^5 \times 3^5\) و \(\Large 4^4 \times 2^4\) را به دست آورید.
حل: توانها مساوی است، بنابراین کافی است پایهها را در یکدیگر ضرب کنیم:
\(\LARGE 2^5 \times 3^5=(2 \times 3)^5=6^5\)
\(\LARGE 4^4 \times 2^4=(4 \times 2)^4=8^4\)
مثال از درسنامهٔ ساده کردن عبارت های توان دار هفتم
مثال 5: عبارات \(\Large 35^6\) و \(\Large 21^5\) را به صورت حاصل ضرب توانهایی از اعداد اول بنویسید.
حل: میتوانیم از عکس قانونی که برای ضرب اعداد تواندار با توان مساوی گفتیم استفاده کنیم. یعنی میتوانیم بنویسیم:
\(\LARGE 35^6=(7 \times 5)^6=7^6 \times 5^6\)
\(\LARGE 21^5=(3 \times 7)^5=3^5 \times 7^5\)
مثال از درسنامهٔ ساده کردن عبارت های توان دار هفتم
مثال 6: عبارت \(\Large 15^3 \times 9^2 \times 5^3 \times 3^4\) را به صورت حاصل ضرب توانهایی از اعداد اول بنویسید.
حل: ابتدا \(\Large 15\) و \(\Large 9\) به صورت حاصل ضرب اعداد اول نوشته و عبارت را ساده میکنیم:
\(\LARGE 15^3 \times 9^2 \times 5^3 \times 3^4\)
\(\Large =(3 \times 5)^3 \times (3 \times 3)^2 \times 5^3 \times 3^4\)
\(\Large =3^3 \times 5^3 \times 3^2 \times 3^2 \times 5^3 \times 3^4\)
حال، توان عباراتی را که دارای پایههای یکسان هستند، با یکدیگر جمع میکنیم:
\(\LARGE 3^3 \times 5^3 \times 3^2 \times 3^2 \times 5^3 \times 3^4\)
\(\LARGE =3^{3+2+2+4} \times 5^{3+3} \)
\(\LARGE =3^{11} \times 5^6 \)
مثال از درسنامهٔ ساده کردن عبارت های توان دار هفتم
مثال7: عبارت \(\Large 5^2 \times 3^4 \times 5^2\) را ساده کنید.
حل: \(\Large 5^2 \times 5^2\) قابل سادهسازی است. همان طور که گفتیم، هم میتوان توان را ثابت در نظر گرفته و پایهها را در یکدیگر ضرب کرد. در این صورت، عبارت داده شده را میتوان به صورت زیر ساده کرد:
\(\LARGE 5^2 \times 3^4 \times 5^2\)
\(\LARGE =(5^2 \times 5^2) \times 3^4\)
\(\LARGE =25^2 \times 3^4\)
هم میتوان پایه را ثابت در نظر گرفته و توانها را با یکدیگر جمع کرد:
\(\LARGE 5^2 \times 3^4 \times 5^2\)
\(\LARGE =(5^2 \times 5^2) \times 3^4\)
\(\LARGE =5^4 \times 3^4\)
\(\LARGE =(5 \times 3)^4\)
\(\LARGE =15^4\)
در این مسئله، روش دوم، کمک بیشتری در سادهسازی به ما کرد. البته در هر مسئلهای میتوانیم با توجه به نیازی که داریم عمل کنیم.
توصیه میشه قبل خوندن این پست، پستهای تعریف عدد تواندار ومحاسبه عبارتهای تواندار رو مطالعه کنید ودر ادامه پست جذر وریشه رو بخونید.
زنگ آخر کلاس محاسبه عبارت توان دار هفتم
در درسنامهای که از ریاضی هفتم خواندیم، با محاسبهٔ ضرب عبارتهای تواندار با پایههای مساوی و ضرب عبارتهای تواندار با توانهای مساوی آشنا شدیم. همان طور که دیدید، در صورتی که پایهها مساوی باشند، توانها را با یکدیگر جمع میکنیم. در صورتی هم که توانها مساوی باشند، پایهها را در هم ضرب میکنیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با ساده کردن عبارت های توان دار هفتم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.




