چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!

تعجب نکنید، در این درس با یک خانواده و رابطه پدر و فرزندانش آشنا می‌شویم. بله، حق دارید؛ شما با چهار ضلعی ها از پیش‌دبستانی هم آشنا بوده‌اید! از وقتی هم چشم باز کرده‌اید، این شکل‌های هندسی را گوشه گوشه خانه و همه جا دیده‌اید. شاید بگویید مربی مهدکودک هم این درس را به من داد و من هم داخل چهارضلعی را رنگ‌آمیزی کردم، اما صبر کنید! سال‌ها گذشته و الان شما زبان جدیدی به نام زبان ریاضی یاد گرفته‌اید، پس بیایید این بار به زبان ریاضی در مورد ویژگی چهار ضلعی ها حرف بزنیم.

در این درس از سری آموزش ریاضی پایه هشتم ، با خواص چند چهارضلعی مهم یعنی متوازی الاضلاع، لوزی، مستطیل، مربع و ذوزنقه آشنا شده و با استفاده از ویژگی‌های این شکل‌های هندسی، نوع چهارضلعی را تشخیص می‌دهیم.

چهار ضلعی ها : عضو مهم خانواده چندضلعی‌ها

در درسنامه خط تقارن آموختیم که به هر خط‌شکسته بسته‌ای که اضلاع آن یکدیگر را بجز در رأس‌های شکل قطع نکند، چندضلعی گفته می‌شود.

در آن درس با چندضلعی‌های مختلفی از جمله چهار ضلعی ها روبرو شدیم؛ پس به سادگی می‌توان گفت چهار ضلعی، به چندضلعی با 4 رأس، 4 ضلع و 4 زاویه داخلی گفته می‌شود.

این شکل‌ها در هندسه و همچنین معماری و ساختمان‌سازی کاربردهای فراوانی دارند. در ادامه به ویژگی متوازی الاضلاع، لوزی، مستطیل، مربع و ذوزنقه خواهیم پرداخت.

---

---

متوازی الاضلاع : پدر خانواده چهار ضلعی ها

تعریف متوازی الاضلاع

متوازی الاضلاع به چهار ضلعی گفته می‌شود که ضلع‌های روبروی آن دو به دو با هم موازی‌اند. متوازی الاضلاع \( \Large ABCD \) را در شکل زیر مشاهده می‌کنید:

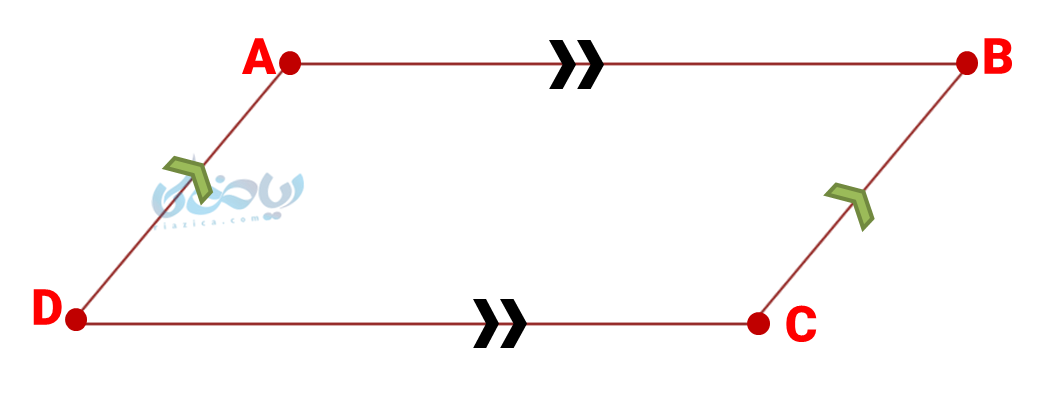
در این متوازی الاضلاع داریم:

\( \Large \overline {AB} \parallel \overline {CD} \)

\( \Large \overline {AD} \parallel \overline {BC} \)

امّا چرا گفتیم متوازی الاضلاع پدر خانواده چهارضلعی ها است؟ چون در ادامه درس خواهید دید که لوزی، مستطیل و مربع نوع خاصی از این شکل هستند.

خواص متوازی الاضلاع

به طور کلی در هر متوازی الاضلاع چند ویژگی به شرح ذیل وجود دارد:

1. ضلع‌های روبرو موازی و مساویند؛
2. زاویه‌های روبرو مساویند؛
3. قطرها یکدیگر را نصف می‌کنند؛
4. زاویه‌های مجاور مکمل‌اند.

اثبات ویژگی های متوازی الاضلاع

اثبات برابری ضلع‌ها و زاویه‌های روبرو

همان‌گونه که در درس خط تقارن مشاهده کردیم، متوازی الاضلاع دارای مرکز تقارن است؛ یعنی با چرخش 180 درجه آن حول مرکز تقارن، شکل روی خودش منطبق می‌شود.

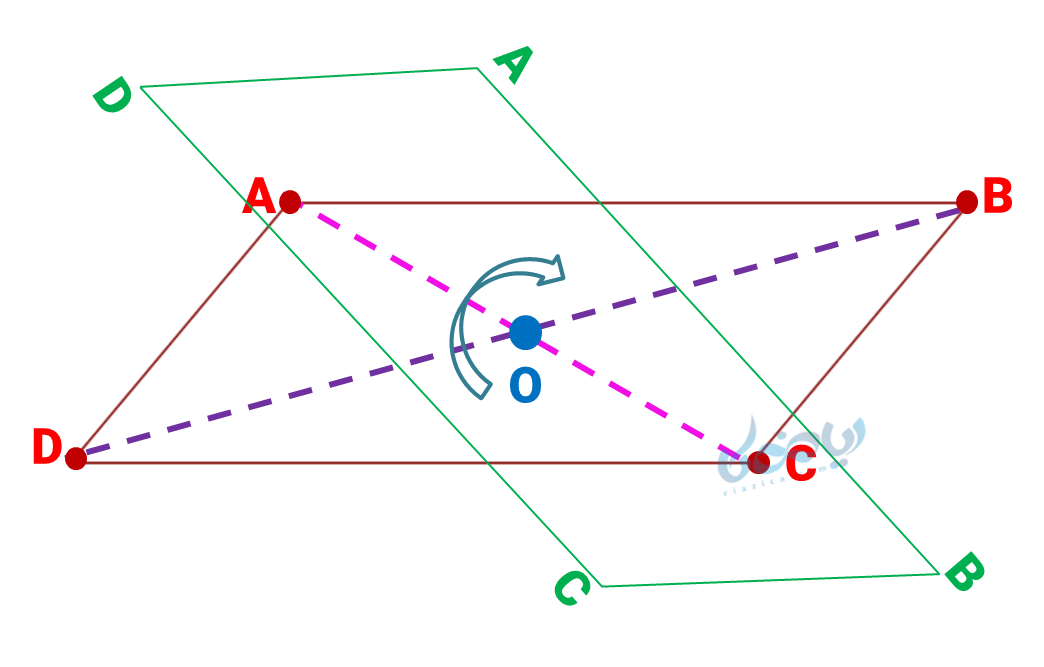
اگر چهار ضلعی \( \Large ABCD \) که یک متوازی الاضلاع با مرکز تقارن \( \Large O \) است، مطابق شکل بالا حول مرکز تقارن به اندازه 180 درجه دوران دهیم، رأس \( \Large A \) روی \( \Large C \) و رأس \( \Large B \) روی \( \Large D \) منطبق می‌شود؛ بنابراین:

\( \Large \hat A = \hat C \)

\( \Large \hat B = \hat D \)

که نشان می‌دهد زاویه‌های روبرو در متوازی الاضلاع با هم برابرند.

همچنین با این دوران، ضلع \( \Large \overline {AD} \) روی ضلع \( \Large \overline {BC} \) و ضلع \( \Large \overline {AB} \) روی ضلع \( \Large \overline {CD} \) قرار خواهد گرفت؛ پس خواهیم داشت:

\( \Large \overline {AD} = \overline {BC} \)

\( \Large \overline {AB} = \overline {CD} \)

که نشان می‌دهد اضلاع روبرو در متوازی الاضلاع با هم برابرند.

اثبات نصف شدن قطرها

اگر به شکل دقت کنیم می‌بینیم که با دوران 180 درجه، پاره‌خط‌های \( \Large \overline {OA} \) و \( \Large \overline {OC} \) روی هم و همچنین پاره‌خط‌های \( \Large \overline {OB} \) و \( \Large \overline {OD} \) نیز روی هم قرار می‌گیرند.

\( \Large \overline {OA} = \overline {OC} \)  (نصف شدن پاره‌خط\( \Large \overline {AC} \) )

\( \Large \overline {OB} = \overline {OD} \)  (نصف شدن پاره‌خط\( \Large \overline {BD} \) )

در درسنامه همنهشتی مثلث ها نهم اثبات برابری اضلاع روبه رو و منصف بودن قطرها را از راه همنهشتی مثلثها نیز می توانید مطالعه کنید.

از درس زاویه های داخلی و خارجی می‌دانیم که مجموع زاویه‌های داخلی یک چهار ضلعی برابر با 360 درجه است. یعنی در متوازی الاضلاع بالا:

\( \Large \hat A + \hat B + \hat C + \hat D = 360° \)

از سوی دیگر دیدیم که زاویه‌های روبرو برابرند؛ یعنی:

\( \Large \hat A = \hat C \)

\( \Large \hat B = \hat D \)

با جای‌گذاری این برابری‌ها در عبارت اول خواهیم داشت:

\( \Large \hat A + \hat B + \hat A + \hat B = 360° \)

\( \Large → 2( \hat A + \hat B) = 360° \)

\( \Large → \hat A + \hat B = \frac {360°}{2} \)

\( \Large → \hat A + \hat B = 180° \)

پس زاویه‌های مجاور \( \Large \hat A \) و  \( \Large \hat B \)، مکمل یکدیگرند.

توجه کنید که در عبارت‌های بالا اگر به جای \( \Large \hat A \)، \( \Large \hat C \) و به جای \( \Large \hat B \)، \( \Large \hat D \) قرار دهیم، به نتیجه زیر هم می‌رسیم.

\( \Large → \hat C + \hat D = 180° \)

نکته: برابری زاویه‌های روبرو و مکمل بودن زاویه‌های مجاور برای چهارضلعی متوازی الاضلاع در درس خطوط موازی و مورب هم با روشی دیگر اثبات شد.

مثال ترکیبی چهار ضلعی ها با مبحث حل معادله درجه اول

مثال 1: در شکل‌های زیر با تشکیل معادله، مقادیر \( \Large x \) و \( \Large y \) را بدست آورید.

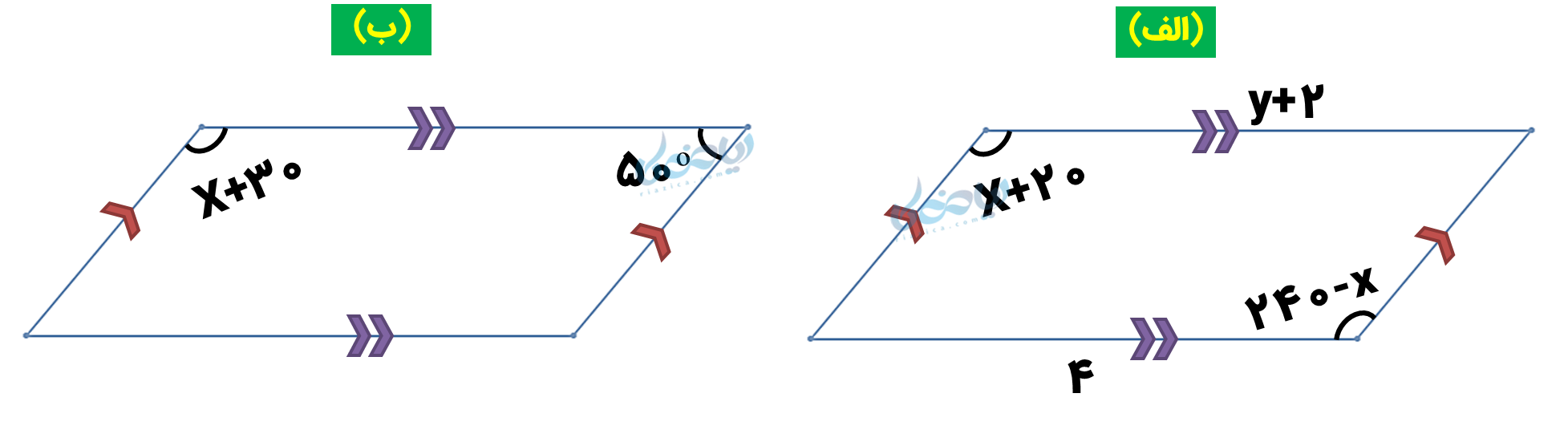
حل 1:

الف)

می‌دانیم که در متوازی الاضلاع ضلع‌ها و زاویه‌های روبرو با هم برابرند؛ پس در این شکل دو ضلع روبرو و دو زاویه روبرو را با هم برابر می‌نویسیم تا بتوانیم مجهولات را بدست آوریم:

\( \Large y + 2 = 4 \) (برابری ضلع‌های روبرو)

\( \Large → y = 4 -2 = 2 \)

\( \Large x + 20 = 240 – x \) (برابری زاویه‌های روبرو)

\( \Large → x + x = 240 – 20 \)

\( \Large → 2x = 220 \)

\( \Large → x = \frac {220}{2} = 110° \)

ب)

برای حل این مثال از خاصیت مکمل بودن زاویه‌های مجاور در متوازی الاضلاع استفاده کرده و با تشکیل معادله مقدار \( \Large x \) را محاسبه می‌کنیم:

\( \Large (x+30) + (50) = 180° \)

\( \Large → x = 180 – 50 -30 \)

\( \Large → x = 100° \)

مستطیل : پسر ارشد خانواده چهار ضلعی ها

تعریف مستطیل

مستطیل، متوازی الاضلاعی با زاویه‌های قائمه است. این نوع چهار ضلعی که در شکل زیر نشان داده شده است، از طرفی همگی ویژگی‌های متوازی الاضلاع را دارد و از سوی دیگر دارای 4 زاویه °90 است.

داستان این خانواده را فراموش نکنید… این پسر ارشد خانواده، مانند پدرش متوازی الاضلاع است و به وصیت او مانند پدر قدخمیده‌اش نیست. در شکل زیر ببینید که مستطیل همان متوازی الاضلاعی است که دو ضلعش صاف شده!

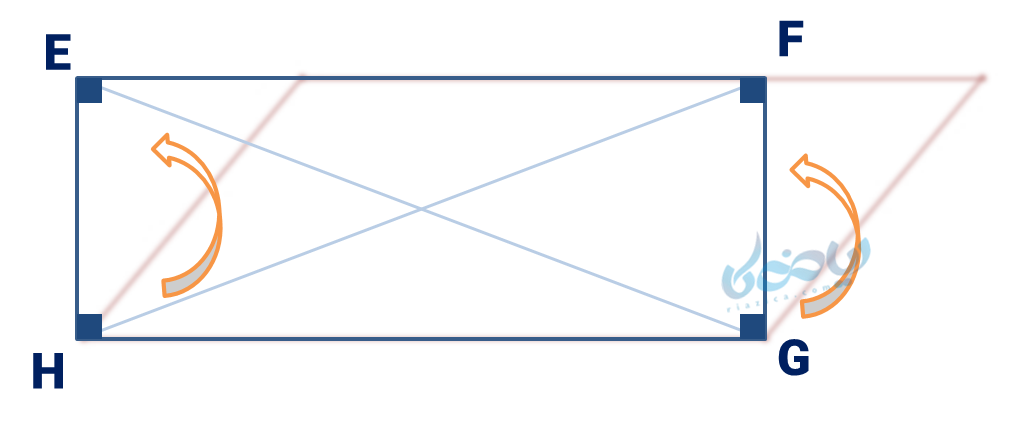
خواص مستطیل

مستطیل چند خاصیت به صورت زیر دارد:

1. همگی ویژگی‌های گفته شده برای متوازی الاضلاع ؛
2. زاویه‌های مستطیل قائمه‌اند؛
3. دو قطر مستطیل برابرند.

بنابراین در مستطیل بالا، روابط زیر برقرار است:

\( \Large \hat E = \hat F = \hat G = \hat H = 90° \) (زوایای قائمه)

\( \Large \overline {EG} = \overline {FH} \) (دو قطر برابر)

لوزی : دختر بزرگ خانواده چهار ضلعی ها

تعریف لوزی

لوزی، نوعی متوازی الاضلاعی با چهار ضلع برابر است.

به داستان برگردیم! دختر بزرگ خانواده، شبیه پدرش شده و ویژگی‌های او را دارد. یعنی ضلع‌های روبرو در لوزی نیز با هم مساویند. البته او از پدر یاد گرفته که عدالت را رعایت کنید؛ برای همین 4 ضلع مساوی دارد.

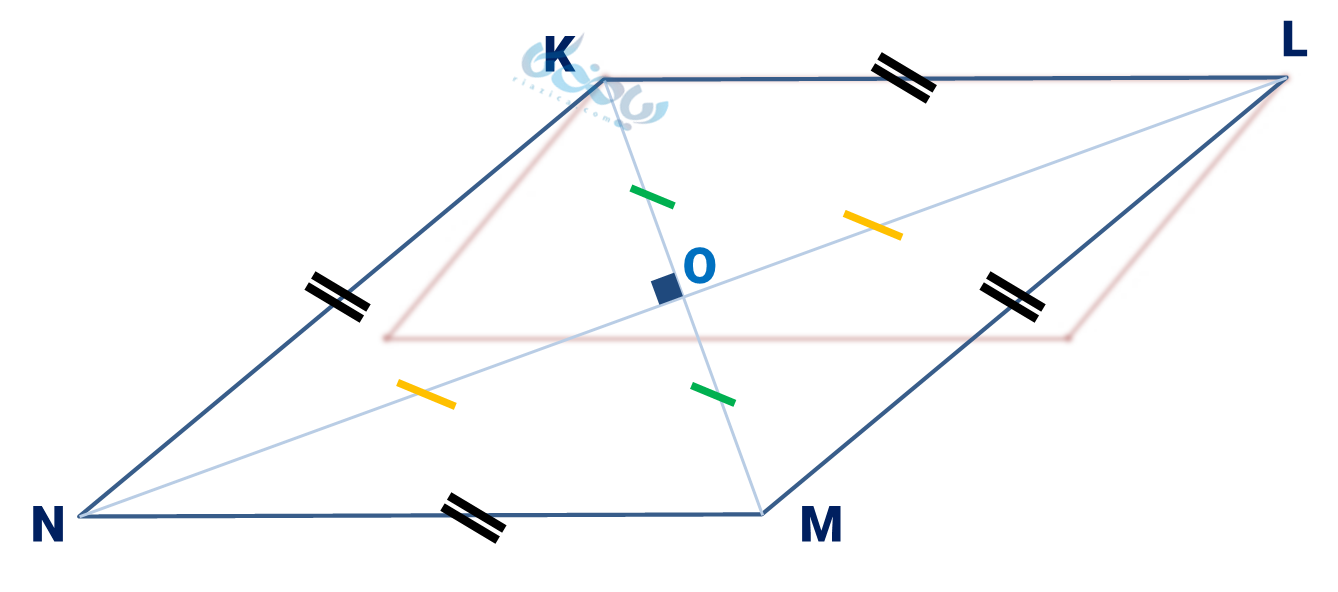
خواص لوزی

لوزی چند ویژگی به صورت زیر دارد:

1. همگی ویژگی‌های گفته شده برای متوازی الاضلاع ؛
2. هر چهار ضلع لوزی با هم برابرند؛
3. قطرهای لوزی عمودمنصّف یکدیگرند.

پس برای لوزی نشان داده شده در بالا می‌توان روابط زیر را نوشت:

\( \Large \overline {KL} = \overline {LM} = \overline {MN} = \overline {NK} \) (برابری اضلاع)

\( \Large \overline {OK} = \overline {OM} \) (عمودمنصّف بودن قطرها)

\( \Large \overline {OL} = \overline {ON} \)

\( \Large \overline {KM} \perp \overline {LN} \)

مثال 2: چهارضلعی زیر یک لوزی است؛ مقادیر \( \Large x \) و \( \Large y \) را بدست آورید.

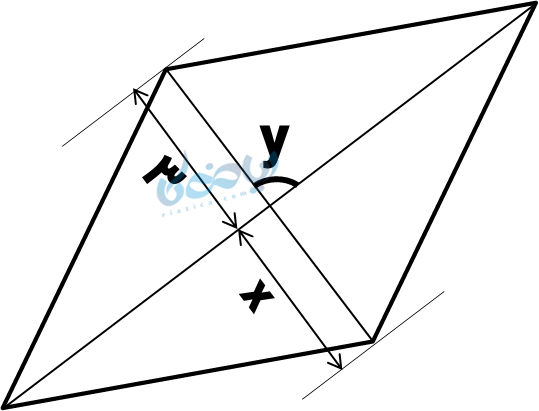
حل 2:

یاد گرفتیم که در لوزی قطرها عمودمنصّف یکدیگرند، این یعنی هم قطرها با هم زاویه قائمه می‌سازند ( زاویه \( \Large \hat y \) ) و هم یکدیگر را نصف می‌کنند (یعنی دو نصف نشان داده شده با هم برابرند).

\( \Large \hat y = 90° \)

\( \Large x = 3 \)

---

---

مربع : فرزند کوچک خانواده چهار ضلعی ها

تعریف مربع

مربع، متوازی الاضلاعی با چهار ضلع برابر و زاویه‌های قائمه است.

مربع فرزند کوچک خانواده چهارضلعی ها بسیار منظم و مؤدب است. هم ویژگی‌های پدرش متوازی الاضلاع را دارد و هم شبیه برادر بزرگترش مستطیل زاویه‌های 90 درجه دارد و هم شبیه خواهرش لوزی دارای چهار ضلع مساوی است.

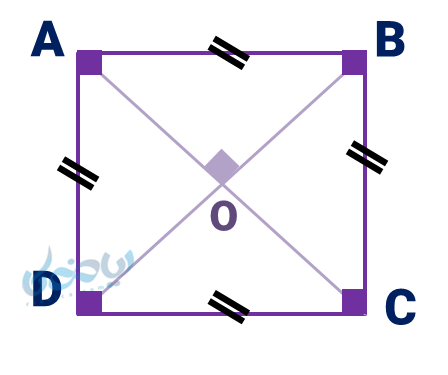
خواص مربع

مربع دارای ویژگی‌هایی به شرح ذیل است:

1. همگی ویژگی‌های گفته شده برای متوازی الاضلاع ؛
2. هر چهار ضلع مربع با هم برابرند؛
3. زاویه‌های مربع قائمه‌اند؛
4. قطرهای مربع با هم برابرند؛
5. قطرهای مربع عمودمنصّف یکدیگرند.

پس برای مربع نشان داده شده در بالا می‌توان نوشت:

\( \Large \overline {AB} = \overline {BC} = \overline {CD} = \overline {DE} \) (برابری اضلاع)

\( \Large \hat A = \hat B = \hat C = \hat D = 90° \) (زوایای قائمه)

\( \Large \overline {OA} = \overline {OC} \) (عمودمنصّف بودن قطرها)

\( \Large \overline {OB} = \overline {OD} \)

\( \Large \overline {AC} \perp \overline {BD} \)

نکته: رابطه بین ویژگی‌های متوازی الاضلاع، مستطیل، لوزی و مربع را می‌توان بصورت شکل زیر خلاصه کرد:

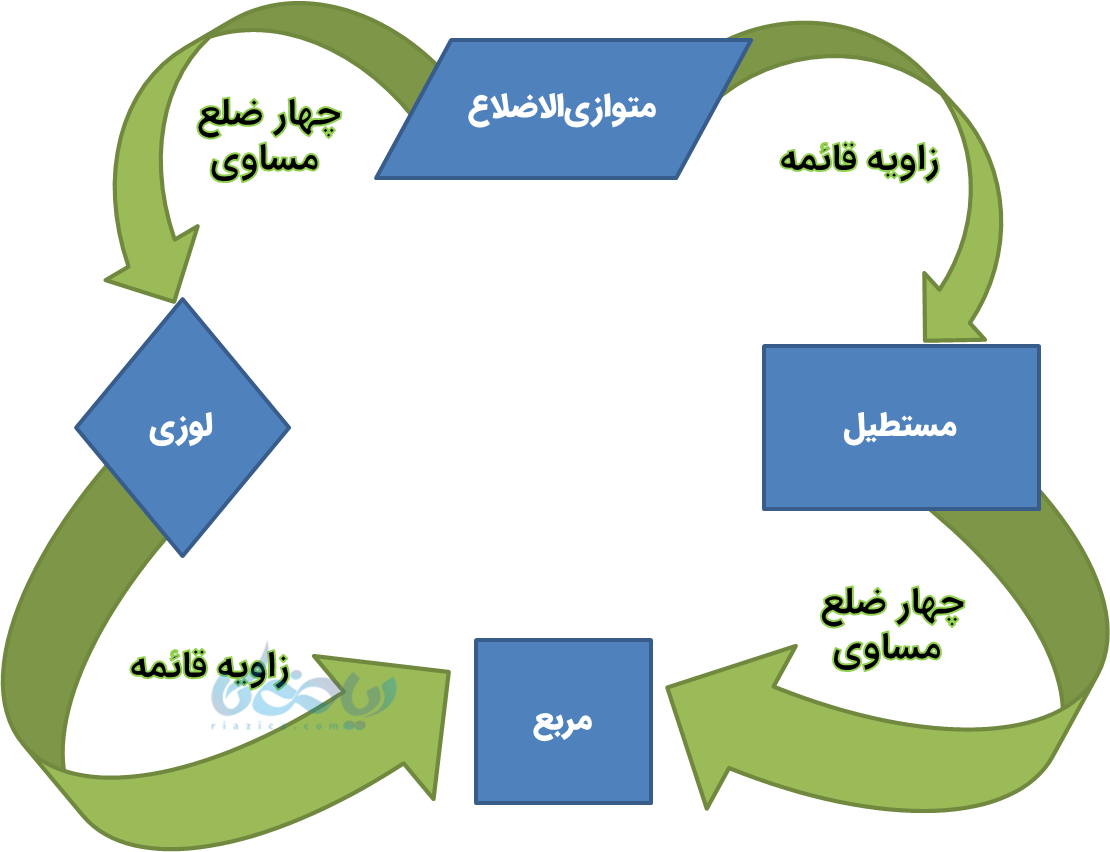
از این شکل نتایج زیر بدست می‌آید:

• لوزی، مستطیل و مربع هرکدام نوعی متوازی الاضلاع هستند؛
• مربع نوعی مستطیل است؛
• مربع نوعی لوزی است.

مثال 3: جدول زیر را برای چهار ضلعی ها کامل کنید:

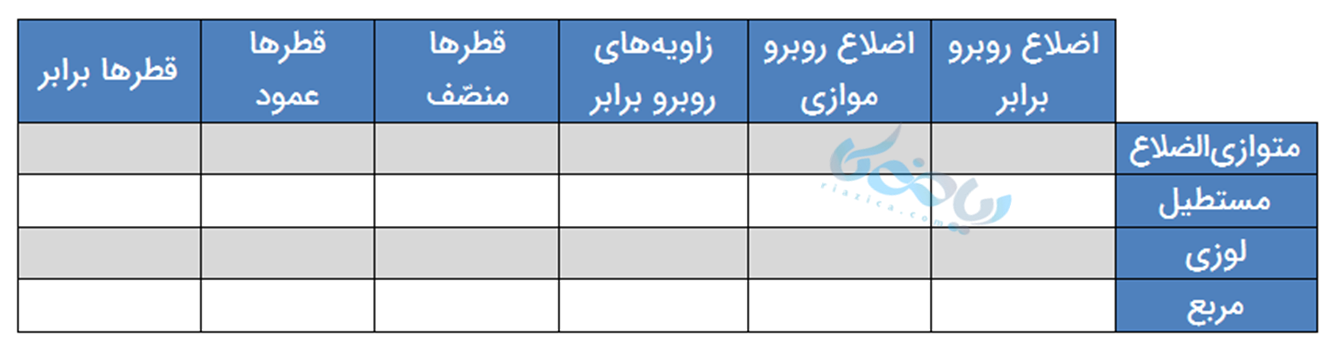
حل 3:

با توجه به خواص گفته شده برای شکل‌های هندسی در این درس، جدول داده شده بدین صورت کامل می‌گردد:

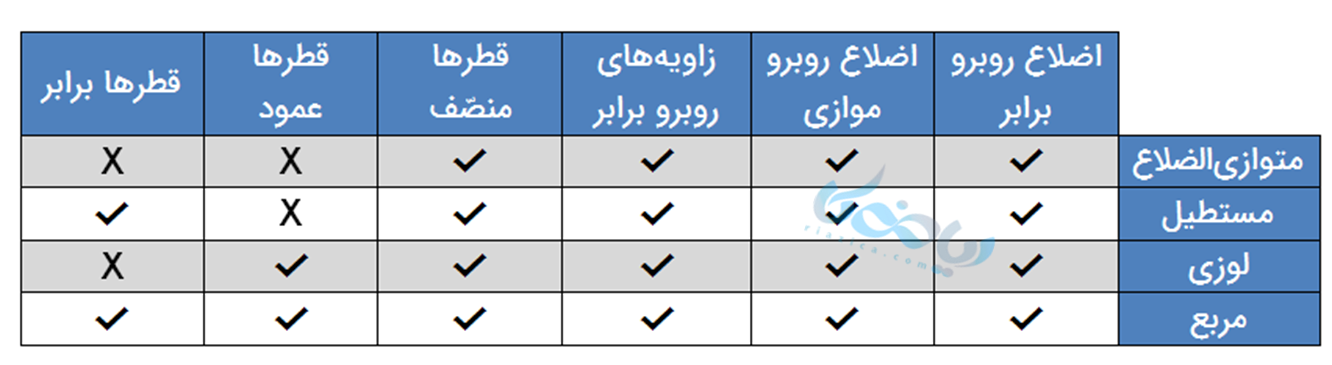
ذوزنقه : همسایه‌ای که دوست دارد شبیه خانواده چهار ضلعی ها باشد.

ذوزنقه چهارضلعی است که تنها دو ضلع آن با هم موازیند.

ذوزنقه همسایه خانواده است که خیلی دوست داشت که شبیه آن‌ها باشد، ولی نتوانست دو عضو روبروی موازی داشته باشد.

در شکل بالا چهارضلعی \( \Large ABCD \) یک ذوزنقه است؛ چون دو ضلع آن با هم موازیند؛ برای این ذوزنقه می‌توان نوشت:

\( \LARGE \overline {AB} \parallel \overline {CD} \) (توازی دو ضلع)

انواع ذوزنقه

دو نوع خاص از ذوزنقه به شرح ذیل وجود دارد:

1. ذوزنقه متساوی الساقین؛
2. ذوزنقه قائم الزاویه.

خواص ذوزنقه متساوی الساقین

ذوزنقه متساوی الساقین که در شکل بصورت چهار ضلعی \( \Large EFGH \) نشان داده شده است،  دارای ویژگی های زیر است:

1. دو ساق آن با هم برابرند؛
2. زاویه‌های مجاور هر قاعده با هم برابرند؛
3. زاویه‌های مجاور ساق مکمل یکدیگرند.

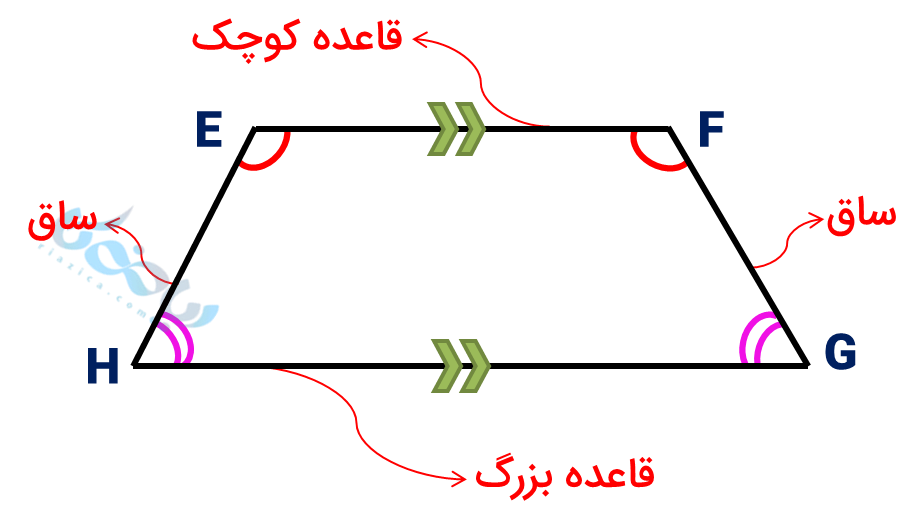
در این ذوزنقه می‌توان نوشت:

\( \LARGE \overline {EF} \parallel \overline {GH} \) (توازی دو ضلع)

\( \LARGE \overline {EH} = \overline {FG} \) (برابری دو ساق)

\( \LARGE \hat E = \hat F \) (برابری زوایای مجاور قاعده کوچک)

\( \LARGE \hat H = \hat G \) (برابری زوایای مجاور قاعده بزرگ)

\( \Large → \hat E + \hat H = 180° \) (مکمل بودن زوایای مجاور ساق چپ)

\( \Large → \hat F + \hat G = 180° \) (مکمل بودن زوایای مجاور ساق راست)

خواص ذوزنقه قائم الزاویه

چهار ضلعی \( \Large QRST \) یک ذوزنقه قائم الزاویه را نشان می‌دهد؛ این نوع ذوزنقه دارای زاویه قائمه است.

\( \LARGE \overline {QR} \parallel \overline {ST} \) (توازی دو ضلع)

\( \Large → \hat Q = \hat T = 90° \) (قائمه بودن زاویه)

چهار ضلعی ها و خط تقارن

خط تقارن و مرکز تقارن در چهارضلعی ها

مرکز تقارن هر چهار شکل هندسی در وسط آن قرار دارد. متوازی الاضلاع خط تقارن ندارد؛ لوزی و مستطیل هر کدام 2 خط تقارن و مربع 4 خط تقارن دارند. مرکز و محور تقارن چهار ضلعی ها را در شکل زیر مشاهده می‌کنید:

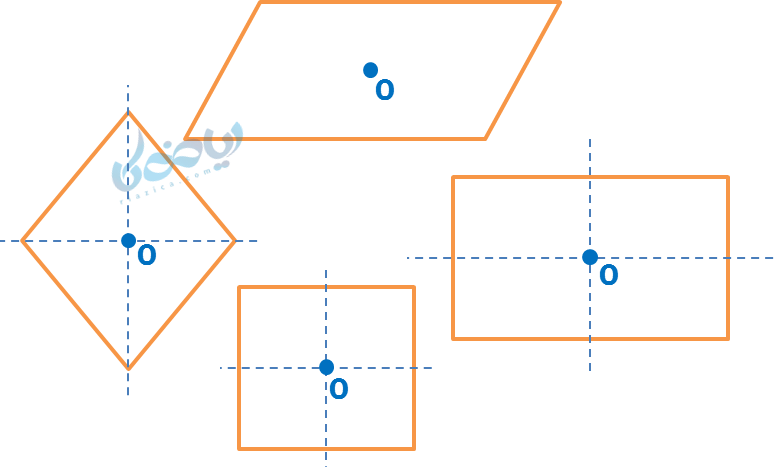
تشخیص چهارضلعی ها به کمک خط تقارن

گاهی در این درس، سؤالاتی مطرح می‌شود که از شما می‌خواهد در یک شکل چهارضلعی موردنظر را تشخیص دهید. برای توضیح این مطلب از یک مثال کمک می‌گیریم.

مثال 4: از وصل کردن وسط اضلاع مربع \( \Large ABCD \)، چهار ضلعی \( \Large PQRS \) بدست آمده است. \( \Large PQRS \) چه نوع شکل هندسی است؟

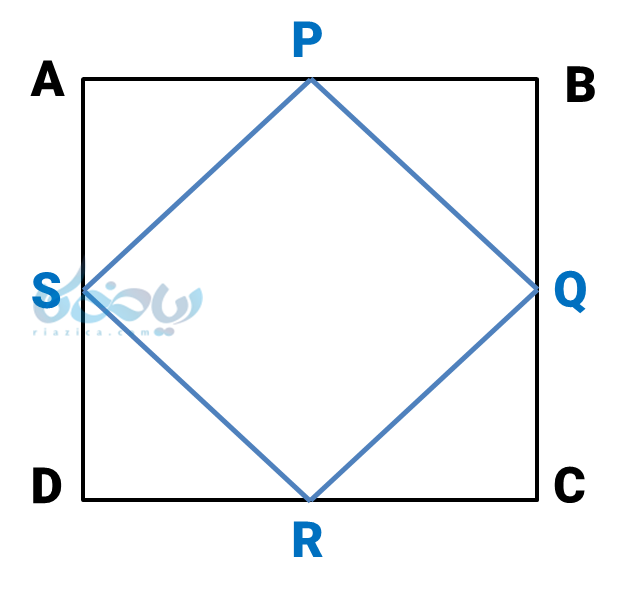
حل 4:

در این‌گونه سؤالات، محورهای تقارن شکل اصلی را در نظر بگیرید و شکل را روی محورهای تقارن تا بزنید؛ در شکل وسط:

• اگر ضلع‌ها روی هم منطبق شوند (یعنی ضلع‌ها برابرند): شکل وسط، لوزی است.
• اگر زاویه‌ها روی هم منطبق شوند (یعنی زاویه‌ها برابرند- و چون مجموع زوایای چهارضلعی 360 درجه است، همه زاویه‌ها قائمه‌اند): شکل وسط، مستطیل است.
• اگر هم زاویه‌ها روی هم منطبق شوند و هم ضلع‌ها (یعنی چهار ضلع برابرند و زاویه‌ها 90 درجه‌اند): شکل وسط، مربع است.

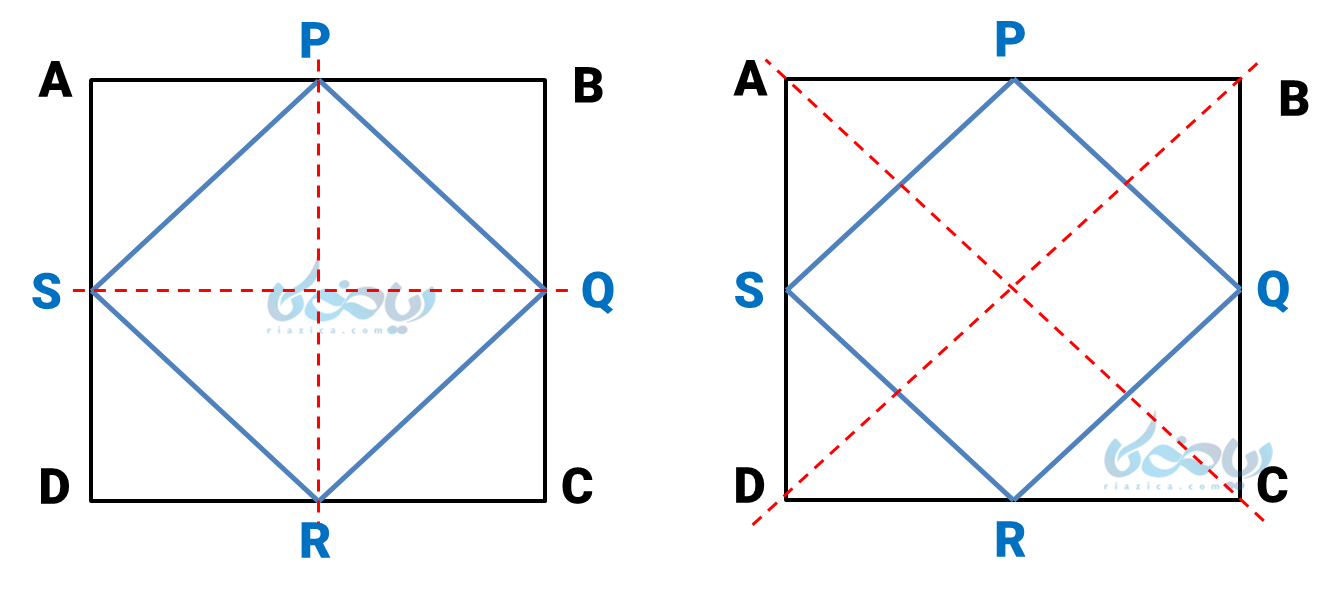
در این مثال، بیایید مربع را روی چهار خط تقارنش تا بزنیم؛ اگر این تا زدن را برای خطوط تقارن سمت چپ (وسط اضلاع) انجام دهیم به شکل زیر خواهیم رسید:

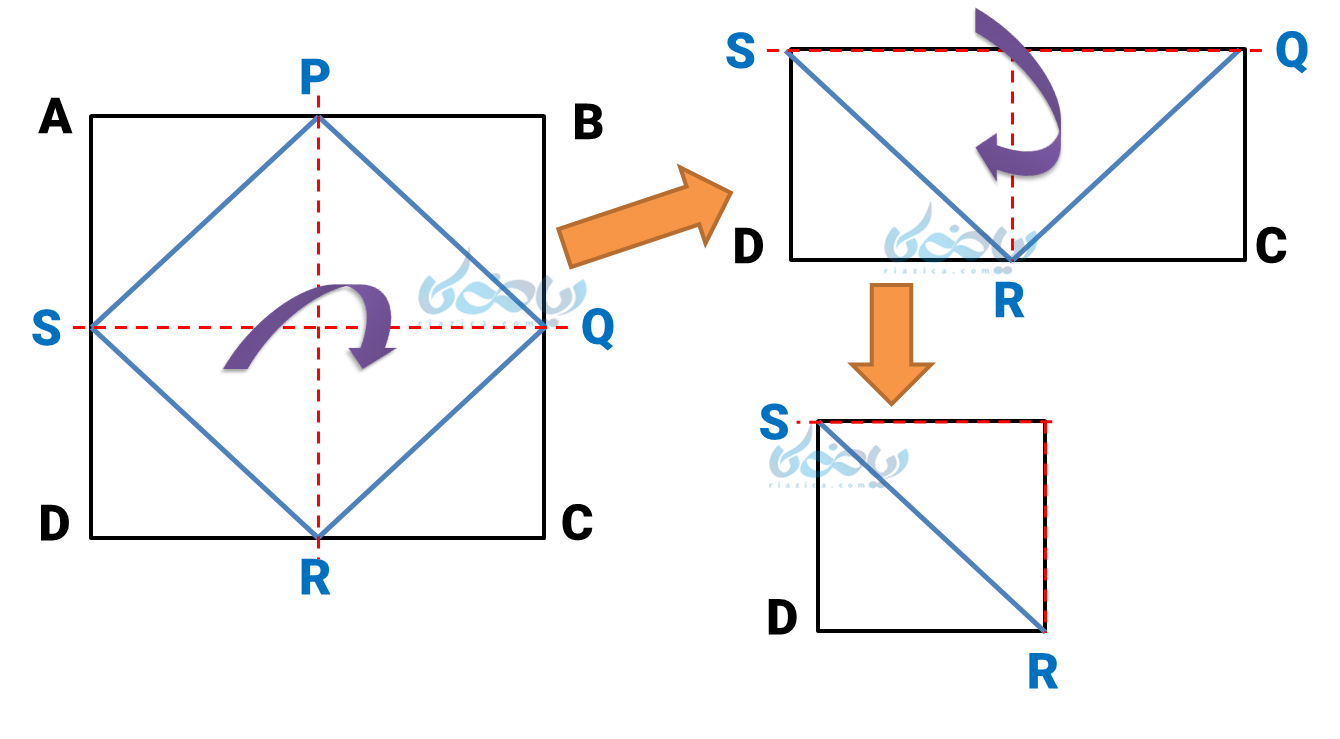
مشاهده می‌کنیم که در این حالت همه اضلاع روی هم افتاده و نهایتاً تنها ضلع \( \Large \overline {SR} \) دیده می‌شود؛ بنابراین همه ضلع‌های \( \Large PQRS \) با هم برابرند و این شکل لوزی است.

از طرفی اگر شکل را روی خطوط تقارن (قطرها) تا بزنیم، به شکل زیر می‌رسیم:

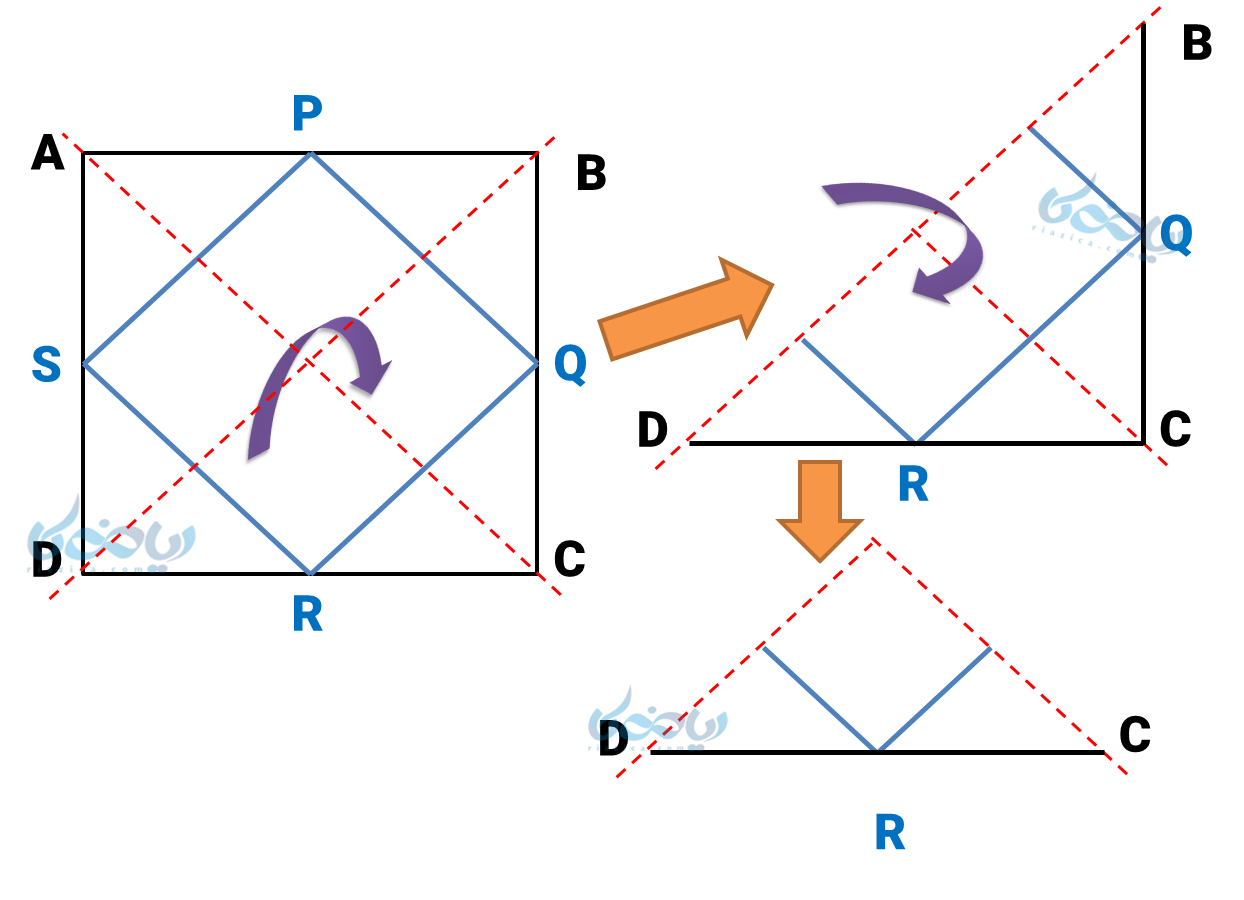
در این حالت همه زاویه‌های \( \Large PQRS \) روی هم منطبق شده (زاویه \( \Large \hat S \)) و نشان می‌دهد همه زوایا برابرند؛ پس این شکل مستطیل است.

گفتیم اگر هر دو حالت رخ دهد، شکل مربع خواهد بود؛ بنابراین چهارضلعی \( \Large PQRS \) یک مربع است. این مسائل را از طریق همنهشتی مثلثها نیز می توان حل نمود

زنگ آخر کلاس چهار ضلعی ها

در این درسنامه با خانواده‌ چهار ضلعی ها آشنا شدیم؛ پدر این خانواده، متوازی الاضلاع بود که ویژگی‌های او را فرزندانش یعنی لوزی، مستطیل و مربع به ارث برده‌اند. به علاوه همسایه آن‌ها یعنی ذوزنقه و انواع آن را شناختیم. همچنین روش تشخیص یک چهارضلعی به کمک خط تقارن را آموختیم. با مثال‌هایی که در این درس حل کردیم، از این درس با قدرت عبور خواهیم کرد.

در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.

---

---

به خوندن ادامه بده!

زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعی‌ها!