فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارت‌های جبری استفاده کن!

این درسته که ریاضی یعنی اعداد؛ ولی همیشه هم قرار نیست فقط با اعداد کار کنیم. گاهی عبارت‌های جبری خودشون حرف می‌زنند! در این درس از مجموعه آموزش ریاضی پایه هشتم ، با روش فاکتورگیری ریاضی هشتم در عبارت‌های جبری آشنا می‌شویم و خواهیم توانست با تبدیل عبارت جبری به ضرب، آن را تجزیه کنیم. همچنین نحوه پیدا کردن مقدار یک عبارت جبری را یاد گرفته. خواهیم دید چگونه از عبارت‌های جبری برای اثبات مسائل در ریاضی کمک بگیریم.

پیدا کردن مقدار عبارت‌های جبری

اجازه دهید قبل از رسیدن به موضوع فاکتورگیری ریاضی هشتم ، یاد بگیریم چگونه مقدار عبارت جبری را محاسبه کنیم. برای بدست آوردن مقدار عددی عبارت‌های جبری کافی است به جای متغیرها (همون حروف!)، اعداد داده شده را قرار دهیم. سپس با انجام عملیات ریاضی، جواب را بدست آوریم.

در واقع عبارت‌های جبری شبیه یک ماشین عددساز عمل می‌کنند. این ماشین عددی را به عنوان ورودی می‌گیرند، بر روی آن عملیات ریاضی انجام می‌دهند و جواب را بصورت خروجی تحویل می‌دهند:

این ماشین، عدد وارد شده را ابتدا دو برابر کرده و سپس با سه جمع می‌کند؛ پس عدد 5، ابتدا دو برابر شده (10=) و سپس با سه جمع می‌شود (13=).

---

---

تشخیص متغیر در عبارت جبری

حرفی که به تنهایی یک طرف تساوی قرار می‌گیرد، خروجی است (حواستان باشد! همیشه خروجی، \( \Large y \) نیست). مثلاً در تساوی زیر، \( \Large y \) متغیر و \( \Large x \) همان خروجی ماشین عددساز است:

\( \Large x= 2y^2 + 1 \)

مثال 1: مقدار عددی \( \Large y= – \frac {1}{2}x + 1 \) را به ازای \( \Large x= 2 \) بدست آورید.

حل 1:

\( \Large y= – \frac {1}{2} × (2) + 1 \)

\( \Large y= – 1 + 1 = 0 \)

مثال 2: مقدار عددی عبارت‌های جبری زیر را به ازای مقادیر داده شده محاسبه کنید:

\( \Large b= 2a^2 + 5 \text {   (a= 0 , 1 , 2)} \)  (الف

\( \Large y= 2x – z \text {   (y= 2 ,  z=4)} \)  (ب

حل2:

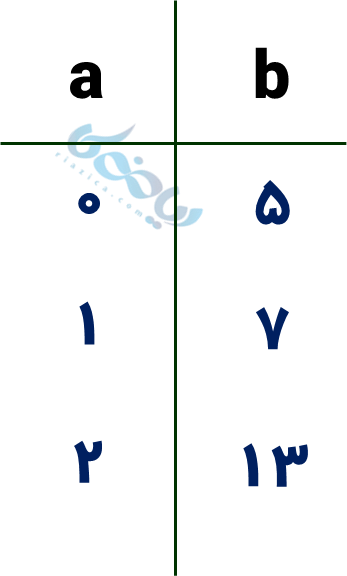
الف) در اینجا متغیر، \( \Large a \) است، پس باید مقدار \( \Large b \) را به ازای مقادیر مختلف \( \Large a \) با جای‌گذاری این مقادیر در آن بدست آوریم. جدولی رسم می‌کنیم و این مقادیر را در آن‌ها می‌نویسیم:

 (به ازای 0) \( \Large b= 2 × (0)^2 + 5 \)

\( \Large = 0 + 5 = 5 \)

(به ازای 1) \( \Large b= 2 × (1)^2 + 5 \)

\( \Large = 2 + 5 = 7 \)

(به ازای 2) \( \Large b= 2 × (2)^2 + 5 \)

\( \Large = 8 + 5 = 13 \)

ب) در این مثال، هرجا \( \Large x \) دیدیم، به جای آن 2 و هرجا \( \Large z \) دیدیم، به جای آن 4 قرار می‌دهیم، تا مقدار \( \Large y \) بدست آید:

\( \Large y= 2 × (2) – 4 = 4-4=0 \)

حدس عبارت جبری از روی ورودی و خروجی

اگر متغیرها (همان عددهای ورودی و خروجی ماشین عددساز!) مشخص باشند، می‌توانیم عبارت جبری موردنظر را حدس بزنیم. یعنی حدس بزنیم چه عملیات ریاضی روی یک عدد انجام شده تا به عدد خروجی رسیده است. به مثال زیر توجه کنید:

مثال 3: عبارت جبری را با توجه به ورودی و خروجی حدس بزنید.

حل 3:

باید عبارت جبری پیدا کنیم که با قرار دادن عدد 3 در آن، جواب 5 و با قرار دادن عدد 5، جواب 11 شود. باید حدس بزنیم؛ یعنی در ذهن خودمان عبارت‌های جبری مختلفی امتحان کنیم؛ مثلاً:

• عدد 3 با 2 جمع شده و جواب 5 بدست آمده است. امتحان کنیم، آیا برای عدد بعد هم درست است؟ می‌بینیم اگر عدد 6 را با 2 جمع کنیم، جواب 11 نمی‌شود. پس این صحیح نیست!
• عدد 3 ضربدر \( \Large \frac{5}{3} \) شده و حاصل 5 است. آیا برای عدد دیگر هم برقرار است؟ اگر 6 را در \( \Large \frac{5}{3} \) ضرب کنیم، جواب 10 است. پس این حدس هم درست نبود!
• عدد 3 ابتدا در 2 ضرب شده و سپس 1 واحد از آن کم شده است (5=). آیا برای عدد دیگر هم صحیح است؟ خب بیایید امتحان کنیم:

\( \Large (6 × 2) – 1 = 12-1=11 \)

درست است! پس عبارت جبری می‌نویسیم که \( \Large x \) در 2 ضرب شده و سپس 1 واحد از آن کم شود؛ یعنی:

\( \Large y = 2x – 1 \)

اثبات مسائل ریاضی به کمک عبارت‌های جبری

معمولاً برای اثبات در ریاضی، از عبارت‌های جبری استفاده می‌شود، یعنی به جای خود اعداد از حروف و عبارت‌های کلی استفاده می‌شود. برای فهم این موضوع به مثال زیر توجه کنید:

مثال 4: ثابت کنید ضرب دو عدد زوج، همواره عددی زوج است. (اثبات جمع دو عدد را در بخش فاکتورگیری ریاضی هشتم با مثال خواهیم دید.)

حل 4:

خب! برای شروع بیایید ابتدا چند عدد را امتحان کنیم:

\( \Large 2 × 4 = 8 \)

\( \Large 10 × 6 = 60 \)

\( \Large 8 × 12 = 96 \)

این نمونه‌ها همگی نشان دادند که دو عدد زوج در هم ضرب شده و حاصل، عددی زوج شده است؛ امّا آیا همین چند مورد کافی است؟ خیر! باید در حالت کلی اثبات شودنه فقط با زدن مثال، بنابراین از عبارت‌های جبری استفاده می‌کنیم.

برای این کار، عبارت جبری که عددی زوج را نشان دهد می‌نویسیم (یادتون میاد؟ بالاتر، بخش الگوهای عددی). عدد اول را برابر \( \Large 2m \) و عدد دوم را برابر \( \Large 2n \) در نظر می‌گیریم:

\( \Large 2m × 2n = 4mn \)

حاصلضرب این دو عدد زوج برابر \( \Large 4mn \) شده است که عددی زوج است، چون ضریب 4 دارد. پس در کل ثابت کردیم حاصل‌ضرب دو عدد زوج، عددی زوج است.

وقتی از روش جبری وکلی مسائل را اثبات می کنیم (استدلال استنتاجی) اثبات محکم ومنطقی می باشد که کسی به روند اثبات ایرادی نمی تواند بگیرد.

فاکتورگیری ریاضی هشتم

فاکتورگیری یعنی (تبدیل به ضرب) یا (تجزیه)! برای این کار به روش فاکتورگیری ریاضی هشتم طبق مراحل زیر عمل می‌کنیم:

1. بزرگترین شمارنده مشترک (ب.م.م) ضرایب را بدست می‌آوریم؛ (یادآوری : ب.م.م ریاضی هفتم)
2. حروف مشترک با توان کمتر را در کنار (ب.م.م) ضرایب می‌نویسیم؛ (تا اینجا، جمله مشترک بدست آمده)
3. همه جملات عبارت را بر جمله مشترک تقسیم کرده و درون پرانتز پس از آن می‌نویسیم.

مثال 5: عبارت‌های زیر را به ضرب تبدیل کنید.

\( \Large 42xy^3 – 35x^2y^2 \) (الف

\( \Large a ×3^x – 5 × 3^x \) (ب

حل 5:

الف) ب.م.م اعداد 42 و 35 برابر است با 7؛ چون:

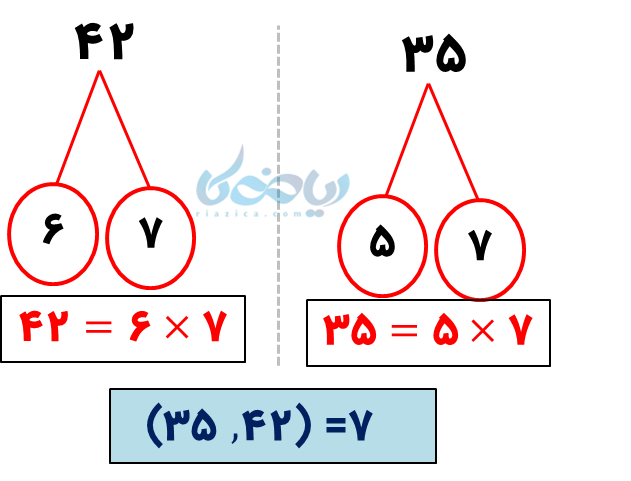
توان \( \Large x \) در جمله اول، 1 و در جمله دوم، 2 است؛ همچنین توان \( \Large y \) در جمله اول، 3 و در جمله دوم، 2 است. پس حروف مشترک با توان‌های کمتر، \( \Large xy^2 \) خواهد بود.

بنابراین  \( \Large 7xy^2 \) را قبل از پرانتز گذاشته و جمله به جمله را بر آن تقسیم کرده و درون پرانتز می‌نویسیم:

\( \Large 7xy^2 (6y^2 – 5x) \)

ب) ضریب عبارت \( \Large a × 3^x \) برابر است با 1؛ پس باید ب.م.م اعداد 1 و 5 را بدست آوریم که برابر است با 1. حروف مشترک بین دو جمله \( \Large 3^x \) است، پس آن را قبل از پرانتز می‌نویسیم:

\( \Large 3^x (a– 5) \)

---

---

مقلوب یک عدد

اگر یک عدد دو رقمی را بصورت \( \Large \overline {ab} \) نشان دهیم، آن‌گاه به عدد  \( \Large \overline {ba} \)، مقلوب آن گفته می‌شود (یعنی جای یکان و دهگان عوض شده است). به عنوان مثال مقلوب عدد 18، برابر با 81 و مقلوب عدد 73 برابر با 37 است.

نکته: عدد دو رقمی \( \Large \overline {ab} \) را می‌توانیم بصورت گسترده بنویسیم:

\( \Large \overline {ab} = 10 a + b \)

چون \( \Large a \) دهگان و \( \Large b \) یکان این عدد است.

ویژگی مجموع و تفاضل یک عدد با مقلوب خودش

مثال 6: نشان دهید که جمع یک عدد دو رقمی با مقلوب آن، مضرب 11 است.

حل 6:

در بخش‌های بالاتر یاد گرفتیم که برای اثبات ریاضی، به جای اعداد از عبارت‌های جبری استفاده می‌شود. مجموع یک عدد دو رقمی با مقلوب آن را بدین صورت نشان می‌دهیم:

\( \Large \overline {ab} + \overline {ba} \)

حال به جای \( \Large \overline {ab} \) ، ( \( \Large  10 a + b \) ) و به جای \( \Large \overline {ba} \)  ، ( \( \Large  10 b + a \) ) جای‌گذاری می‌کنیم:

 \( \Large (10 a + b) + (10 b + a) \)

\( \Large = 11 a + 11 b \)

توجه کنید که برای جمع جمله‌های بالا، طبق روش ساده کردن عبارت‌های جبری، جملات مشابه را با هم جمع کرده‌ایم.

از روش فاکتورگیری ریاضی هشتم استفاده می‌کنیم: (ب.م.م) ضرایب برابر با 11 است و حروف مشترکی وجود ندارد؛ پس این عبارت بدین صورت نوشته می‌شود:

\( \Large = 11 (a + b) \)

که نشان می‌دهد جمع یک عدد دو رقمی با مقلوب آن، مضرب 11 است؛ چون عدد 11 در یک عدد (جمع دو عدد داخل پرانتز) ضرب شده است.

مثال 7: نشان دهید که تفاضل هر  عدد دو رقمی از مقلوبش، بر 9 بخش‌پذیر است.

حل 7:

مشابه مثال بالا عمل می‌کنیم و تنها به جای علامت جمع، علامت تفریق قرار می‌دهیم:

\( \Large \overline {ab} – \overline {ba} \)

 \( \Large = (10 a + b) – (10 b + a) \)

\( \Large = 9 a – 9 b \)

طبق روش فاکتورگیری ریاضی هشتم حاصل این عبارت برابر است با:

\( \Large = 9 (a – b) \)

که نشان می‌دهد تفاضل یک عدد دو رقمی از مقلوبش، بر 9  بخش‌پذیر است.

تجزیه عبارت‌های جبری در ریاضیات پایه‌های بالاتر

در ریاضیات پایه دهم خواهیم دید، فاکتورگیری تنها یکی از روش‌های تجزیه عبارت‌های جبری است. در درس تجزیه عبارت‌ های جبری به 4 روش مختلف با 4 روش مختلف برای تجزیه عبارت جبری آشنا خواهیم شد.

ساده کردن کسرها به کمک فاکتورگیری ریاضی هشتم

یکی از هزاران کاربرد فاکتور گیری وتجزیه عبارتهای جبری ساده کردن عبارتهای گویا(کسری) می باشدبه مثال زیر دقت کنید:

مثال 8: کسر زیر را تا جای ممکن ساده کنید.

\( \LARGE \frac {a^2b – ab^2}{a^3b^2 – a^2b^3} \) 

حل 8:

برای ساده کردن این کسر، ابتدا صورت و مخرج را تجزیه می‌کنیم. جملات عبارت‌های جبری صورت و مخرج همگی دارای ضریب 1 هستند، پس ب.م.م آن‌ها 1 خواهد بود.

حروف مشترک صورت، \( \Large ab \) و حروف مشترک مخرج \( \Large a^2b^2 \) است، پس هر یک را این‌گونه تجزیه می‌کنیم:

\( \Large a^2b – ab^2 = ab (a-b) \)

\( \Large a^3b^2 – a^2b^3 = a^2b^2 (a-b) \)

حال عبارات تجزیه شده را در صورت و مخرج جای‌گذاری می‌کنیم، جمله\( \Large (a-b) \) هم در صورت و هم در مخرج دیده می‌شود، پس خط می‌خورد:

\( \LARGE \frac {ab (a-b)}{a^2b^2 (a-b)} \)

\( \LARGE = \frac {ab}{a^2b^2} \)

صورت و مخرج را تقسیم بر \( \Large ab \) می‌کنیم تا این کسر ساده‌تر شود:

\( \LARGE = \frac {1}{ab} \)

چند مثال از درس فاکتورگیری ریاضی هشتم

مثال 9: در فیزیک، انرژی جنبشی یک جسم از رابطه \( \Large K= \frac {1}{2}mV^2 \) محاسبه می‌شود که در آن، \( \Large m \) جرم و \( \Large V \) سرعت جسم را نشان می‌دهند. اگر یک جسم 10 کیلوگرمی با سرعت \( \Large {m}{s} \) 2 حرکت کند، انرژی جنبشی آن را بدست آورید.

حل 9:

نگران نباشید، اینجا هنوز کلاس ریاضی است! این رابطه یک عبارت جبری است که باید به ازای متغیرهای \( \Large m \) و \( \Large V \) عدد جای‌گذاری کنیم. با توجه به اعداد داده شده در صورت سؤال، انرژی جنبشی برابر است با:

\( \Large K= \frac {1}{2} × (10) × (2)^2 \)

\( \Large = 5 × 4 = 20 \)

مثال 10: ثابت کنید مجموع دو عدد فرد، عددی زوج است.

حل 10:

می‌دانیم که برای اثبات، باید از عبارت‌های جبری استفاده کنیم. پس عددهای فرد را به صورت زیر نشان می‌دهیم: (برای یادآوری نحوه نوشتن اعداد زوج و فرد به الگوهای عددی در درس‌نامه ساده کردن عبارت‌های جبری مراجعه کنید)

\( \Large a = 2m – 1 \)

\( \Large b = 2n – 1 \)

حال عدد زوج و فرد را که با حروف \( \Large a \) و \( \Large b \) نشان داده شده است، جمع می‌کنیم:

\( \Large a + b = (2m – 1) + (2n – 1) \)

\( \Large = 2m + 2n – 2 \)

از روش فاکتورگیری ریاضی هشتم  کمک می‌گیریم: ضریب 2 در همه جملات مشترک است، پس (ب.م.م) ضرایب برابر است با 2. حروف مشترکی نداریم، پس همه عبارات را بر 2 تقسیم کرده و در پرانتز پس از 2 می‌نویسیم:

\( \Large a + b = 2(m + n – 1) \)

که نشان می‌دهد جمع دو عدد فرد، مضرب 2 است (یعنی زوج).

برای یادگیری بهتر وبیشتر این مبحث می توانید تجزیه عبارتهای جبری نهم را بخوانید.

زنگ آخر کلاس فاکتورگیری ریاضی هشتم

خب، خسته نباشید! با این همه مثال، فکر نکنم سخت بوده باشه این درس، درسته؟ در این محتوا، یکی از سه درس‌نامه فصل جبر و معادله، یعنی فاکتورگیری ریاضی هشتم را یاد گرفتیم (به همراه درس‌های ساده کردن عبارت‌های جبری و حل معادله درجه اول). دیدیم که با سه مرحله ساده می‌توانیم عبارت جبری را به ضرب تبدیل کنیم؛ کاربرد تجزیه عبارت جبری را در مثال‌های مربوط به اثبات ریاضی خیلی خوب حس کردیم. همینطور الآن می‌توانیم مقدار عددی یک عبارت جبری را پیدا کنیم یا بالعکس: عبارت جبری مربوط به یک عملیات را حدس بزنیم.

در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.

---

---

به خوندن ادامه بده!

ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!