آموزش ریاضی پایه هشتم

جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!

آخرین بروزرسانی در تاریخ 1401/06/05 توسط محمد بحرانی
جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!
14
شهریور

یکی از بازیگران فیلم سینمایی زندگی ما، اعداد هستند. ساعت، تاریخ، نمره درسی، حساب و کتاب، قد، وزن و … با اعداد گفته می‌شوند. اعداد صحیح نیز نقش اصلی این فیلم را بازی می‌کنند. اگر کمی به اطراف خود نگاه کنید با جمع و تفریق اعداد صحیح روبرو خواهید شد. به من بگویید در نانوایی بقیه پول شما چطور محاسبه می‌شود؟ بگذارید همین ابتدا بگویم که کلید این درس، اولویت عملیات ریاضی است.

در این درس از مجموعه آموزش ریاضی پایه هشتم ، با یادآوری تعاریفی در مورد اعداد صحیح به استقبال موضوعات مهمی همچون قرینه، جمع و تفریق اعداد صحیح ، ضرب و تقسیم اعداد صحیح و پیدا کردن راه‌حل مناسب برای محاسبه عبارات خواهیم رفت. البته فراموش نکنید که بدون دانستن اولویت عملیات ریاضی قطعاً راه را اشتباه خواهیم رفت؛ پس حتماً تا پایان همراه این درس‌نامه باشید.

خرید دوره جذاب ویدیویی آموزش ریاضی هشتم 💎🔮

680.000 تومانافزودن به سبد خرید

تعریف اعداد صحیح

این اعداد شامل صفر (0)، اعداد مثبت (مانند 1، 2، 100، 8000 و …) و اعداد منفی (مانند 1-، 2-، 20-، 500- و …) هستند.

بنابراین می‌توان گفت اعداد صحیح از سه دسته تشکیل شده‌اند:

  1. اعداد صحیح مثبت؛
  2. صفر؛
  3. اعداد صحیح منفی.

یک عدد صحیح، سالم است! و هیچ خرده‌ای ندارد (بر خلاف اعداد اعشاری مانند 2/1). به عنوان مثال، اعداد بین عددهای نوشته شده روی محور زیر، غیرصحیح هستند.

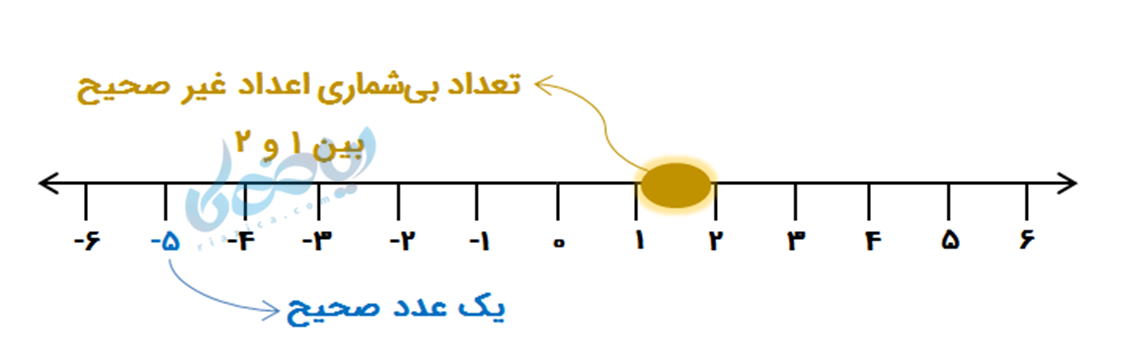
تعریف اعداد صحیح

مجموعه اعداد صحیح، با حرف انگلیسی \( \Large Z \) نشان داده می‌شود:

Z = {…, -3, -2, -1, 0, 1, 2, 3, …}

حال که تعریف اعداد صحیح را با هم مرور کردیم، به موضوع قرینه اعداد پرداخته و پس از آن می‌توانیم جمع و تفریق اعداد صحیح و پس از آن ضرب و تقسیم آن‌ها را با رعایت اولویت عملیات ریاضی یاد بگیریم.

قرینه یک عدد

به اعدادی که فاصله آن‌ها تا مبدأ مختصات (عدد صفر) برابر، اما در جهت مخالف یکدیگر باشند، دو عدد قرینه می‌گویند. به عبارت دیگر، قرینه عدد \( \Large a \) برابر با \( \Large – (a) \) است.

برای فهم بهتر، فرض کنید بر روی مبدأ (عدد صفر)، یک آینه قرار دارد که تصویر هر عدد را نشان می‌دهد. هرچه جسم از آینه دورتر، فاصله تصویرش هم بیشتر!

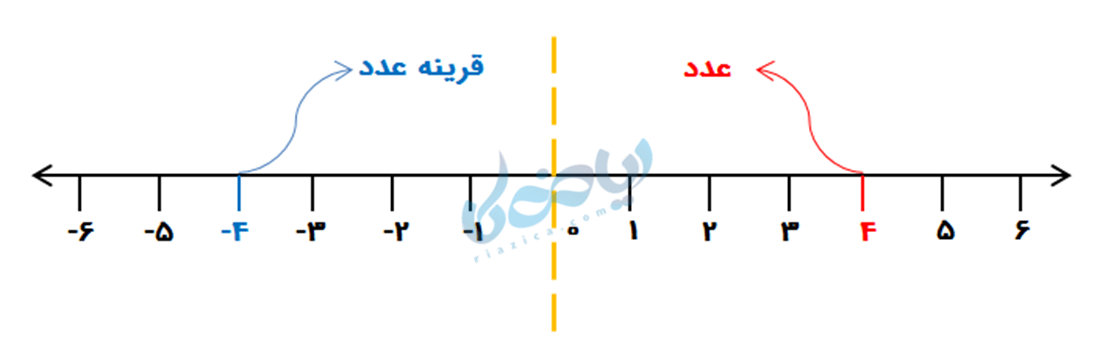
قرینه یک عدد

نکته 1:  قرینه عدد صفر، خود صفر است. (به آینه توجه کنید.)

نکته 2:  با قرینه شدن یک عدد غیر صفر، علامت آن تغییر می‌کند.

نکته 3:  قرینه شدن، فقط برای اعداد صحیح نیست؛ هر عددی را می‌توان قرینه کرد. بنابراین، قرینه کردن اعداد گویا هم مشابه اعداد صحیح است.

مثال 1: قرینه اعداد (20-)، (34) و (0) را بدست آورید. قرینه کدام عدد از مبدأ مختصات فاصله بیشتری دارد؟

حل 1:

همان‌گونه که در بالا یاد گرفتیم، برای قرینه کردن یک عدد کافی است علامت قبل از آن را عوض کنیم. همچنین می‌دانیم قرینه عدد صفر، خود صفر است. بنابراین قرینه اعداد (20-)، (34+) و (0) به ترتیب برابر است با: (20)، (34-) و (0).

فاصله یک عدد تا مبدأ مختصات (صفر)، ربطی به علامت عدد ندارد؛ بلکه مانند آینه‌ای که دیدیم هر عددی که بدون علامت، بزرگتر بود از مبدأ فاصله بیشتری دارد؛ بنابراین:

عدد (20+)، به اندازه 20 واحد و عدد (34-) به اندازه 34 واحد از مبدأ فاصله دارد. عدد صفر نیز دقیقاً روی مبدأ قرار دارد. پس عدد (34-) بیشترین فاصله را خواهد داشت.

انجام عملیات ریاضی روی اعداد صحیح

چهار عمل اصلی (جمع، تفریق، ضرب و تقسیم) در ریاضیات بسیار پرکاربرد هستند. اعداد صحیح را نیز می‌توان با هم جمع، از هم تفریق، در هم ضرب و یا بر هم تقسیم نمود. در ادامه، روش جمع و تفریق اعداد صحیح و ضرب و تقسیم آن‌ها را مرور کرده و همچنین با یادگیری اولویت عملیات ریاضی ، محاسباتی را که چند عملیات مختلف دارند بدون اشتباه انجام خواهیم داد:

جمع و تفریق اعداد صحیح

برای جمع و تفریق اعداد صحیح کافی است مراحل زیر را طی کنیم:

  1. اعداد مثبت را بصورت جداگانه با هم و اعداد منفی را بصورت جداگانه با هم جمع می‌کنیم؛
  2. مجموع اعداد مثبت و مجموع اعداد منفی را از هم کم می‌کنیم؛
  3. برای جواب، علامت عدد بزرگتر را می‌گذاریم.

مثالی از جمع و تفریق در اعداد صحیح با توجه به تعیین علامت

مثال 2: حاصل جمع و تفریق اعداد صحیح در عبارت زیر را بدست آورید:

\( \Large 10 – 83 + (+6) – (-(-9)) \)

حل 2:

برای حل این مثال از دو نکتۀ بالا استفاده می‌کنیم. (6+)+ و ((9-)-)- ضرب علامت‌هاست؛ اولی ضرب مثبت در مثبت است که مثبت می‌شود. برای بدست آوردن دومی، ابتدا داخل پرانتز که ضرب منفی در منفی (مثبت) است را انجام می‌دهیم. سپس ضرب منفی در مثبت، منفی خواهد شد:

\( \Large + (+6) = 6 \)

\( \Large – (-(-9)) = – (+9) = -9 \)

با جای‌گذاری این دو در صورت سؤال:

\( \Large 10 – 83 +6 –9 \)

حال طبق مراحل گفته شده برای جمع و تفریق اعداد صحیح ، ابتدا اعداد هم‌علامت را با هم جمع می‌کنیم:

\( \Large 10 +6 – 83 –9 \)

\( \Large = 16 – 92 \)

سپس مجموع اعداد مثبت (16) و منفی (92) را از هم کم می‌کنیم: 76 = 16 – 92؛ توجه کنید که چون علامت عدد بزرگتر منفی است، علامت حاصل جمع ما منفی خواهد بود: (76-).

ضرب و تقسیم اعداد صحیح – نمونه خلاقانه از جمع و تفریق اعداد صحیح

کته 1 (ضرب و تقسیم علامت‌ها): حاصل ضرب یا تقسیم علامت‌ها در هم بصورت شکل زیر خلاصه می‌شود:

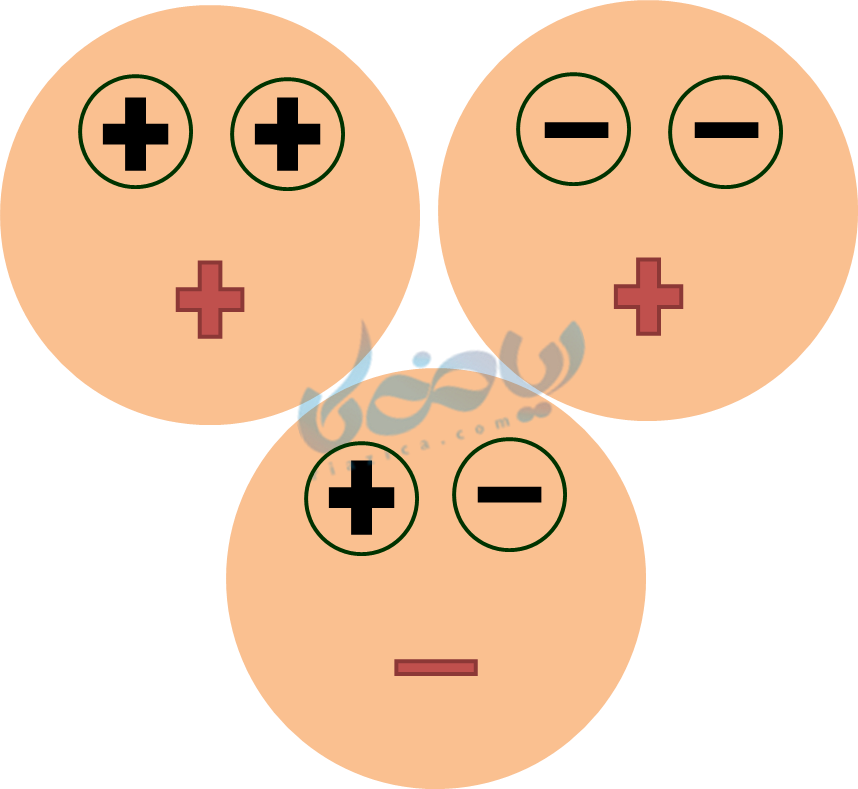
علامت ضرب و تقسیم علامت ها

آدمک اگر چشم هایش شبیه هم باشند، خوشحال است و دهانش مثبت را نشان می دهد؛ اما اگر چشم هایش تا به تا باشد، ناراحت است و دهانش منفی را نشان می دهد.

یعنی حاصل ضرب یا تقسیم علامت‌های شبیه هم، مثبت و حاصل ضرب یا تقسیم علامت‌های غیر مشابه، منفی خواهد بود.

نکته 2: اگر بین یک عدد و پرانتز یا بین یک علامت و پرانتز یا بین دو پرانتز فاصله‌ای نباشد، به معنی ضرب است. به عنوان مثال:

\( \Large -2(-5) = (-2) × (-5) \)

در ضرب و تقسیم اعداد صحیح، ابتدا علامت‌ها را در هم ضرب می‌کنیم. (مطابق نکته ضرب علامت‌ها) و سپس عمل ضرب یا تقسیم را انجام می‌دهیم.

مثال 3: حاصل عبارت‌های زیر را بدست آورید:

\( \Large -4 × (+3) \) (الف)

\( \Large (-28) ÷ (-4) \) (ب)

حل 3:

(الف) علامت یکی منفی و دیگری مثبت است، بنابراین حاصل منفی خواهد بود؛ حال کافی است دو عدد را بدون توجه به علامت در هم ضرب کنیم و علامت منفی را قبل از آن قرار دهیم:

\( \Large -4 × (+3) = – 12 \)

(ب) علامت هر دو عدد منفی است، پس تقسیم این دو، مثبت خواهد بود. برای رسیدن به پاسخ، علامت مثبت را قرار داده و دو عدد را بی‌توجه به علامت‌شان بر هم تقسیم می‌کنیم:

\( \Large (-28) ÷ (-4) = + 7 \)

خرید دوره جذاب ویدیویی آموزش ریاضی هشتم 💎🔮

680.000 تومانافزودن به سبد خرید

اولویت عملیات ریاضی

در برخی عبارت‌های ریاضی هم جمع و تفریق اعداد صحیح و هم ضرب و تقسیم آن‌ها وجود دارد. در این‌گونه محاسبات لازم است ترتیب انجام عملیات را بدانیم. در غیر این صورت حتماً پاسخ را اشتباه بدست خواهیم آورد.

اولویت عملیات ریاضی به ترتیب زیر است:

  1. داخل پرانتز، کروشه، مجموعه و … ؛
  2. توان و جذر؛
  3. ضرب و تقسیم؛
  4. جمع و تفریق.

مثالی مهم از اولویت عملیات ریاضی

مثال 4: حاصل عبارت‌های زیر را بدست آورید:

\( \Large -2^{(2×2)} + 4 × 3 + 2 \) (الف)

\( \Large (32 ÷ 4)^2 +(-3)(-(-2)) \) (ب)

\( \Large + \sqrt {64} × 3 \)

حل 4:

این مثال، ترکیبی از نکات گفته شده در بالا ( اولویت عملیات ریاضی – جمع و تفریق اعداد صحیح – ضرب و تقسیم اعداد صحیح) است:

(الف) گفتیم اولویت اول، محاسبه درون پرانتز، کروشه و … است؛ پس ابتدا به دنبال آن می‌گردیم. در این مثال یک پرانتز در توان قرار دارد. اشتباه نکنیم! نباید اول 2 را به توان 2 برسانیم؛ بلکه ابتدا ضرب درون پرانتز را انجام می‌دهیم:

\( \Large = -2^4 + 4 × 3 + 2 \)

حال دنبال جذر و توان می‌گردیم؛ عبارت اول دارای توان است. اشتباه نکنیم! علامت منفی قبل از 2 را نباید همراه 2 به توان برسانیم، چون این علامت منفی در 2 ضرب شده و یاد گرفتیم که ضرب، پس از توان باید محاسبه شود:

\( \Large = -16 + 4 × 3 + 2 \)

نوبت به ضرب یا تقسیم می‌رسد؛ 4 در 3 ضرب شده است. اشتباه نکنیم! نباید ابتدا 3 را با دو جمع کنیم و سپس در 4 ضرب کنیم، بلکه اول ضرب را انجام می‌دهیم:

\( \Large = -16 + 12 + 2 \)

حال کافی است مطابق روش جمع و تفریق اعداد صحیح عمل کنیم:

\( \Large = -16 + 14 = -2 \)

(ب) در این مثال نیز، مشابه بالا و طبق ترتیب گفته شده عمل می‌کنیم. در قسمت (الف) توضیحات مرحله به مرحله را دیدیم. در این عبارت بدون توضیح، تنها جواب را با هم محاسبه می‌کنیم:

برای تأکید، ((2-)-) را ببینید، از داخلی‌ترین پرانتز شروع کنید: داخل پرانتز اول (2-) است و بیرون آن علامت منفی است که در آن ضرب شده و طبق قانون ضرب علامت‌ها مثبت می‌شود:

\( \Large = 8^2 + (-3)(+2) + \sqrt {64} × 3 \)

\( \Large = 64 + (-3)(+2) + 8 × 3 \)

\( \Large = 64 – 6 + 24 \)

\( \Large = 88 – 6 = 82 \)

پیدا کردن راه‌حل مناسب برای محاسبه یک عبارت

گاهی جمع و تفریق اعداد صحیح بسیار طولانی است؛ در این مواقع لازم نیست تک به تک همۀ اعداد را با هم جمع یا تفریق کنیم؛ می‌توانیم با اندکی دقت، راه‌حل خلاقانه‌ای برای محاسبه آن پیدا کنیم.

برای این که با چنین راه‌حل‌هایی آشنا شوید، چند نمونه را با هم مرور می‌کنیم. دقت کنید که موارد زیر، تنها چند نمونه هستند و شما قطعاً با خلاقیت خودتان می‌توانید مواردی مشابه این مسائل را پیدا کنید.

جمع اعداد متوالی (پشت سر هم)

فرض کنید می‌خواهیم اعداد 1 تا 100 را با هم جمع کنیم. موافقید تک به تک عددها را با هم جمع کنیم؟ اشکالی ندارد! اما زمان خیلی زیادی طول خواهد کشید. بیایید راه‌حل یکی از دانشمندان به نام گاوس (در کودکی‌اش!) را با هم ببینیم:

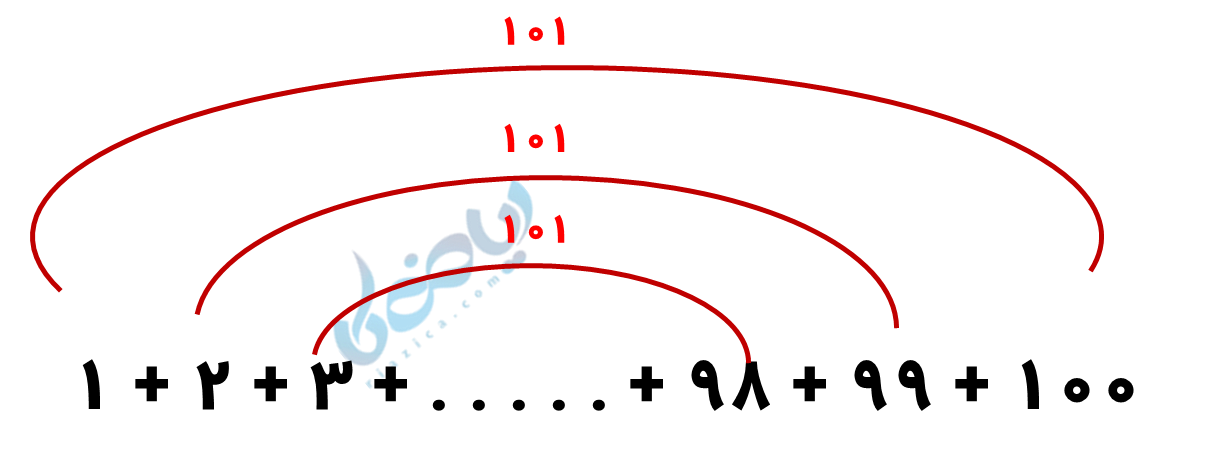
جمع و تفریق اعداد صحیح با اولویت عملیات ریاضی

 

می‌بینید که اگر یک عدد از ابتدا و یک عدد از انتها جمع کنیم، همگی برابر با 101 است. (چند جفت عدد وجود دارد؟ 50 تا. چون 100 عدد داریم). پس حاصل‌جمع اعداد 1 تا 100 برابر خواهد بود با:

\( \Large 1+2+…+99+100 \)

\( \Large = 50 × 101 = 5050 \)

فرمول محاسبه مجموع اعداد در سری منظم اعداد

در محاسبه جمع اعداد یک سری منظم (یعنی تعدادی عدد که فاصله یکسانی از یکدیگر دارند) داریم:

فرمول محاسبه جمع و تفریق اعداد صحیح متوالی

مثال 5: اعداد فرد بین 13 تا 2001 را نوشته و مجموع آن‌ها را محاسبه کنید.

حل 5:

اعداد فرد، یک سری منظم است (چرا؟) چون فاصله بین هر دو عدد برابر مقداری ثابت (2) است. از فرمول بالا استفاده می‌کنیم (عدد اول، 13 و عدد آخر 2001 است):

\( \Large = \frac {2001-13}{2} + 1 \) تعداد اعداد

\( \Large = \frac {1988}{2} + 1 \)

\( \Large = 994 + 1 = 995 \)

\( \Large = \frac {2001+13}{2} × 995 \) مجموع اعداد

\( \Large = \frac {2014}{2} × 995 \)

\( \Large = 1007 × 995 = 1001965 \)

جمع اعداد یکی در میان مثبت و منفی

در این حالت، دو به دو اعداد مثبت و منفی را جمع کنید تا شاید به رابطه‌ای برسید تا سریع‌تر حاصل را بدست آورید.

به عنوان مثال به حاصل‌جمع زیر توجه کنید؛ اعداد زوج بین 10 تا 24 یکی در میان مثبت و منفی با هم جمع شده‌اند.

جمع و تفریق اعداد صحیح یکی در میان غیر هم علامت

می‌بینیم که اگر دو به دو عددهای مثبت و منفی را با هم جمع کنیم، حاصل‌جمع ما تبدیل به 5 تا (2-) شده است؛ یعنی:

\( \Large 10-12+14-16 \)

\( \Large +18-20+22-24 \)

\( \Large = 5 × (-2) = -10 \)

ضرب تعدادی پرانتز

گاهی اگر در ضرب تعدادی عبارت دقت کنیم، خواهیم دید که یکی از عبارات صفر می‌شود. این اتفاق، مسأله را بسیار ساده می‌کند (چرا؟) چون می‌دانیم حاصل‌ضرب عدد صفر در هر عبارتی برابر است با صفر.

مثال 6: حاصل عبارت زیر را محاسبه کنید.

\( \Large (10-1)×(10-2)×… \)

\( \Large …×(10-99)×(10-100) \)

حل 6:

می‌خواهید یکی یکی پرانتزها را محاسبه کنید و در انتها در هم ضرب کنید؟ مشکلی نیست! ولی جواب را نصف شب بدست خواهید آورد!!

کمی دقت کنید: پرانتزها تفریق اعداد از عدد 10 هستند. یکی از همین اعداد خود 10 است. یعنی یکی از پرانتزها (10 – 10) خواهد بود که برابر است با صفر. پس حاصل‌ضرب بقیه پرانتزها هر عددی باشد، ضربدر صفر برابر است با صفر.

توصیه میشه قبل خوندن این پست ، پست جمع وتفریق اعداد صحیح هفتم وضرب وتقسیم اعداد صحیح هفتم رو مطالعه کنید.

زنگ آخر کلاس ضرب و تقسیم اعداد صحیح

راهی که با هم شروع کرده‌ایم، بسیار هیجان‌انگیز است. یادمان باشد که ما با آموختن اعداد صحیح، تازه ایستگاه اول را سپری کردیم، چون مجموعه اعداد زیادی مانند اعداد گویا را قرار است بشناسیم. در این درس با جمع و تفریق اعداد صحیح و ضرب و تقسیم آن، مفهوم قرینه عدد صحیح و اولویت عملیات ریاضی آشنا شدیم. مطمئناً با یادگیری این درس، پایه ساختمان ریاضی ما محکم ساخته شده است.

در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.

خرید دوره جذاب ویدیویی آموزش ریاضی هشتم 💎🔮

680.000 تومانافزودن به سبد خرید

به خوندن ادامه بده!زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعی‌ها!

ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی هشتم به شما پیشنهاد می‌دهیم:
محمد بحرانی

32 دیدگاه برای “جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید! ”

    • دبیر ارشد ریاضیکا گفته:

      با سلام وعرض ادب
      خدا روشکر که مفید هست براتون

      پاسخ
  6. ناشناس گفته:

    سلام
    ببخشید میشه بگید که توی تفریق عامل های تفریق رو چی میگن؟؟

    پاسخ
  8. سیده دینا پیرحیاتی گفته:

    سلام خسته نباشید، ببخشید ما در ریاضی میگیم که منفی پشت پرانتز به معنای قرینه اعداد داخل پرانتز هستش خب من یک سوال دارم آیا اگر در آن پرانتز که منفی پشت پرانتز وجود داشته باشد و در آن پرانتز چند عدد وجود داشته باشد تمام اعداد را قرینه میکنیم یا فقط عدد اولی را قرینه میکنیم، ممنون میشم جواب بدید خیلی برام مهمه.

    پاسخ
    • دبیر ارشد ریاضیکا گفته:

      با سلام وادب
      دوست عزیز تمام جملات داخل پرانتز قرینه میشوند

      پاسخ
  9. F.N گفته:

    سلام
    ۲۴-…..+۲-۴+۶-۸
    اینگونه اعداد رو چگونه حل کنیم
    لطفاً توضیح دهید

    پاسخ
  10. Alisaber گفته:

    سلام تو حل مرحله به مرحله مسئله چهار گزینه ب اول تقسیم رو انجام دادین بعد توان و جذر رو که گویا اول باید توان و جذر انجام بشه بعد تقسیم

    پاسخ
    • دبیر ارشد ریاضیکا گفته:

      سلام دوست عزیز هم علامتها جمع میشن مختلف العلامتها کم میشن همیشه علامت عدد بزرگتر۵-۷=2-

      پاسخ
  13. ناشناس گفته:

    عالی بود من فردا امتحان اغازین ریاضی دارم که از کتاب کلاس هفتم میگیرند منم خب کتابام تحویل داده بودم هشتم گرفته بودم این خیلی کمکم کرد خیلی ممنون

    پاسخ
    • دبیر ارشد ریاضیکا گفته:

      حتما بقیه درسنامه های پایه هشتم رو در طول سال تحصیلی مطالعه کنید

      پاسخ
  15. رضا گفته:

    پسرم یک سوال ریاضی درباره جمع سری اعداد داشت که دنبال راه حل بودم و بین وبسایتهایی که دیدم توضیحات شما عالی بود، هم خودم فهمیدم و هم تونستم به پسرم اموزش بدم
    از طرح خلاقانتون برای ادمکها هم خیلی خوشمون اومد چون به راحتی در ذهن میمونه
    موفق باشید

    پاسخ
    • دبیر ارشد ریاضیکا گفته:

      سلام دوست عزیز
      خوشجالیم که تونستیم برای آموزش دانش آموزان کشور گامی برداریم

      پاسخ

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *