آموزش ریاضی پایه هشتم
خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
رسیدیم به خطوط موازی و مورب ؛ یکی از موضوعات بسیار پرتکرار، کاربردی و در عین حال ساده در هندسه! این مطلب را از دست ندهید، قرار است با سرسره خطها حرکت کنیم، خطهای دیگر را قطع کنیم و روی آنها اثر بگذاریم. چه اثری؟ عجله نکنید، کافیست تا پایان، لحظه به لحظه با این درس همراه باشید.
در درسنامه خطوط موازی و مورب از مجموعه آموزش ریاضی پایه هشتم ، ابتدا توازی و تعامد خطوط تعریف شده و سپس با قضیهای بسیار مهم در مورد ایجاد زاویه در اثر تقاطع خط مورب با خطوط موازی آشنا میشوید. در طول این درس با مثالهای مختلفی روبرو میشوید که توان شما را در یادگیری این مبحث افزایش خواهد داد.
تعاریف خطوط موازی و مورب
پیش از این در دروس ریاضیات پایههای قبل، حتی در دوره ابتدایی با مفهوم موازی، عمود و … آشنا شدهایم. برای یادآوری، قبل از رسیدن به نکات مربوط به خطوط موازی و مورب یک بار دیگر تعریف و نماد آنها را مرور میکنیم:
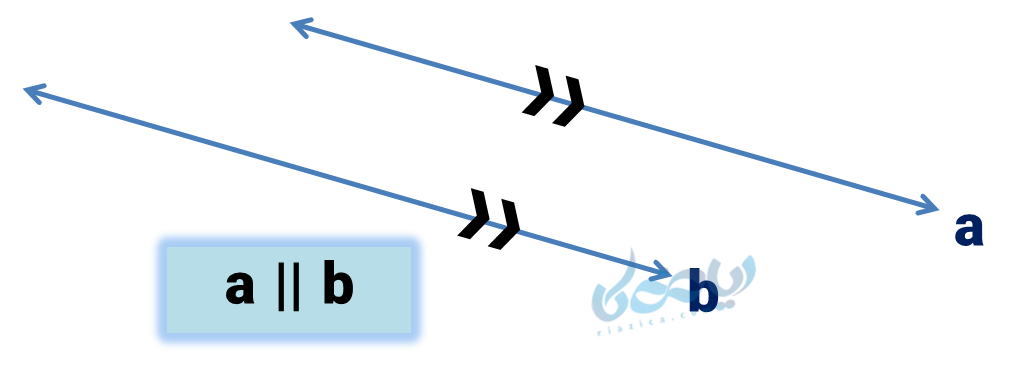
دو خط موازی
دو خط موازی، خطوطی هستند که هرچه آنها را امتداد دهیم، هیچگاه همدیگر را قطع نمیکنند. فاصله دو خط موازی همواره مقداری ثابت است. (توازی؛ یعنی موازی بودن)
موازی بودن (توازی) دو خط \( \Large a \) و \( \Large b \) را بصورت \( \Large a || b \) نشان میدهیم.
دو خط غیرموازی (متقاطع)
خطی که خط دیگر یا امتداد آن را در نقطهای قطع میکند، غیرموازی یا متقاطع با آن خط گفته میشود.
موازی بودن دو خط \( \Large a \) و \( \Large b \) را بصورت \( \Large a \not\parallel b \) نشان میدهیم.

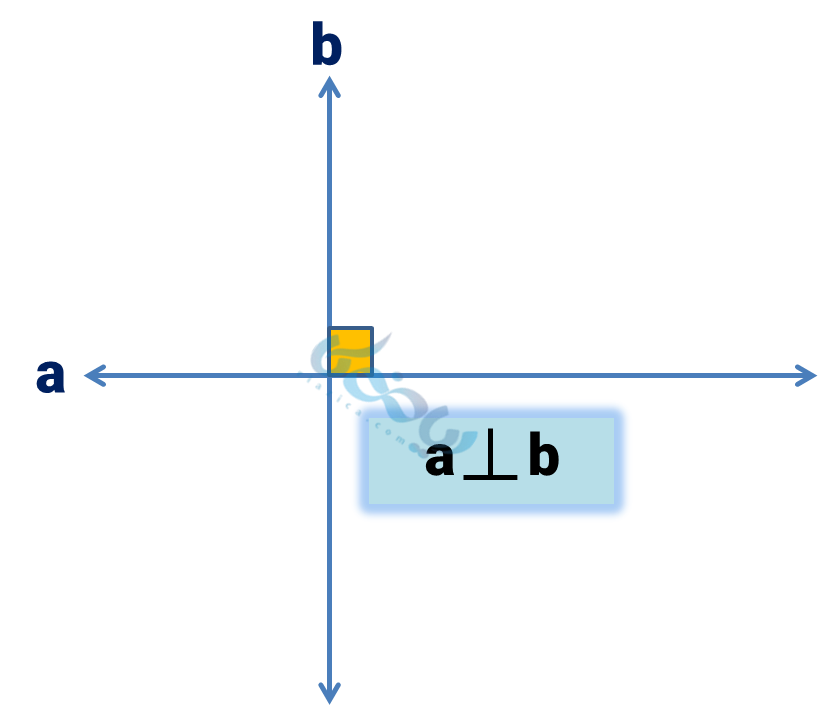
دو خط عمود بر هم
دو خط متقاطع که با هم زاویه °90 میسازند، دو خط عمود بر هم گفته میشوند. (تعامد؛ یعنی عمود بودن)
عمود بودن (تعامد) دو خط \( \Large a \) و \( \Large b \) را بصورت \( \Large a \perp b \) نشان میدهیم.
قضیه خطوط موازی و مورب
پس از مرور تعاریف مربوط به خطوط موازی و مورب نوبت به دو قضیه مهم در مورد خطوط موازی و مورب میرسد. منظور از خط مورب، خطی است که با خط مورد نظر موازی نباشد.
نکته: اگر خط موربی دو خط را قطع کند، مطابق شکل زیر 8 زاویه ایجاد میشود: 4 زاویه تند (\( \Large \hat 2 \)، \( \Large \hat 3 \)، \( \Large \hat 6 \) و \( \Large \hat 7 \) ) و 4 زاویه باز (\( \Large \hat 1 \)، \( \Large \hat 4 \)، \( \Large \hat 5 \) و \( \Large \hat 8 \) ).
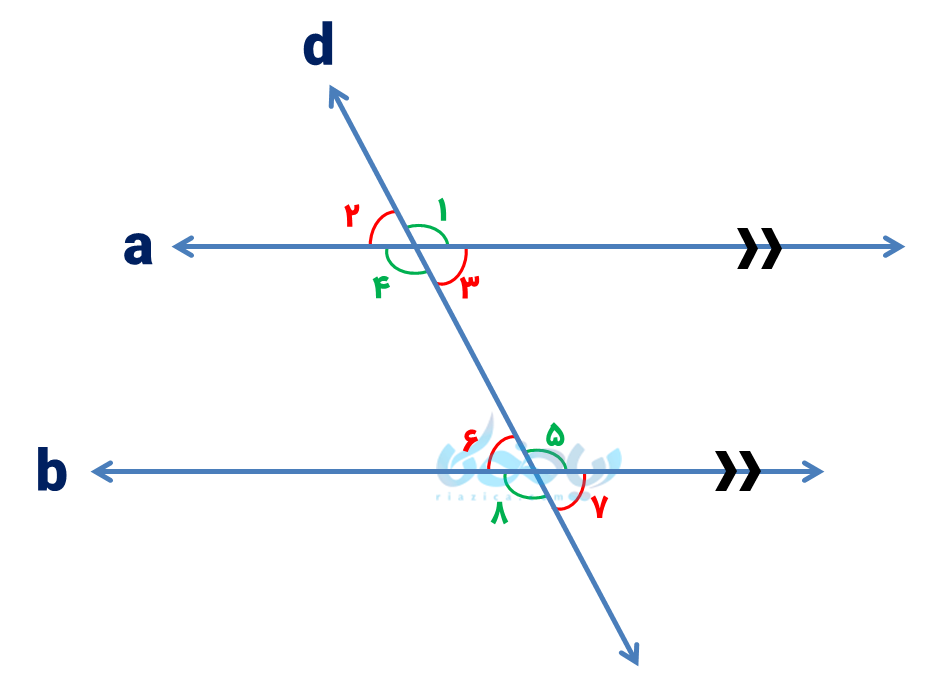
امّا چرا در این شکل بعضی زاویهها با رنگ قرمز و برخی دیگر با رنگ سبز نشان داده شدهاند؟ صبر کنید! دو قضیه خطوط موازی و مورب را با هم بخوانیم تا دلیل آن هم مشخص شود:
قضیه اول خطوط موازی و مورب
اگر یک خط مورب دو خط موازی را قطع کند، با آن دو خط زاویههای مساوی میسازد.
در واقع این خط مورب روی خطوط موازی هشت زاویه که چهار تای آنها تند و برابر وچهار تای آنها زاویه باز و برابرند به وجود می آورد که این زاویه های تند وباز خود با هم مکملند.
قضیه دوم خطوط موازی و مورب (عکس قضیه اول)
اگر خطی مانند \( \Large d \)، خطوط \( \Large a \) و \( \Large b \) را با زاویههای مساوی قطع کند، آنگاه خطهای \( \Large a \) و \( \Large b \) با هم موازیند.
بنابراین در شکل بالا با توجه به موازی بودن خطوط خطهای \( \Large a \) و \( \Large b \) مینویسیم:
( \( \Large a || b \) , مورب \( \Large d \) ) → \( \Large \hat 1 = \hat 5 \)
مثال 1: مشخص کنید که در کدام یک از شکلهای زیر \( \Large a || b \) ؟

حل 1:
طبق قضیه خطوط موازی و مورب باید در هر مورد بررسی کنیم که آیا خط مورب با دو خط زاویه مساوی ساخته است یا نه؟
الف) در این حالت خط مورب \( \Large d \) زاویههای تندی برابر با °80 روی هر دو خط ساخته است، از آنجا که زوایای \( \Large \hat B_1 \) و \( \Large \hat B_2 \) متقابل به رأس هستند:

\( \Large B_1 = B_2 → B_1 = 80° \)
\( \Large → A_1 = B_1 \)
از برابری این دو زاویه نتیجه میگیریم که \( \Large a || b \).
ب) در این حالت اندازه یک زاویه تند و زاویه باز داده شده است. برای بررسی تساوی زاویهها، از این نکته استفاده میکنیم که زوایای \( \Large \hat B_1 \) و \( \Large \hat B_2 \) مکمل یکدیگرند؛ یعنی:
\( \Large B_1 + B_2 = 180° \)
\( \Large B_1 + 150° = 180° \)
\( \Large → B_1 = 180° – 150° = 30° \)
پس زاویه تند ایجاد شده روی خط \( \Large b \) (°30) با زاویه تند ایجاد شده روی خط \( \Large a \) (°35) برابر نیست؛ بنابراین \( \Large a \not\parallel b \).
سایر برابریها
شکل مربوط به قضیه خطوط موازی و مورب را برای راحتی در مطالعه دوباره تکرار میکنیم:

علاوه بر مساوی بودن زوایای 1 و 5 در شکل بالا، بطور کلی وقتی یک خط مورب، دو خط موازی را قطع میکند، زاویههای تند با هم و زاویههای باز با هم برابرند؛ یعنی:
(برابری زاویههای باز) \( \Large \hat 1 = \hat 4 = \hat 5 = \hat 8 \)
(برابری زاویههای تند) \( \Large \hat 2 = \hat 3 = \hat 6 = \hat 7 \)
دلیل برابری زوایا در خطوط موازی و مورب
از قضیههای خطوط موازی و مورب نتیجه گرفتیم که در شکل بالا زاویه 1 با زاویه 5 برابر است. از طرفی زاویه 1 با زاویه 4 متقابل به رأس و همچنین زاویه 5 با زاویه 8 متقابل به رأس هستند:
(زاویه متقابل به رأس) \( \Large \hat 1 = \hat 4 \)
(زاویه متقابل به رأس) \( \Large \hat 5 = \hat 8 \)
پس با توجه به برابری زوایای 1 و 5 نتیجه میگیریم که:
(برابری زاویههای باز) \( \Large \hat 1 = \hat 4 = \hat 5 = \hat 8 \)
اگر به شکل توجه کنیم، میبینیم که زاویههای مکمل در شکل بدین صورت هستند:
(زاویه 1 و 2 مکمل یکدیگرند) \( \Large \hat 1 + \hat 2 = 180° \)
(زاویه 3 و 4 مکمل یکدیگرند) \( \Large \hat 3 + \hat 4 = 180° \)
(زاویه 5 و 6 مکمل یکدیگرند) \( \Large \hat 5 + \hat 6 = 180° \)
(زاویه 7 و 8 مکمل یکدیگرند) \( \Large \hat 7 + \hat 8 = 180° \)
با توجه به برابری زاویههای 1، 4، 5 و 8 و جایگذاری در چهار تساوی بالا، نتیجه میگیریم که:
(برابری زاویههای تند) \( \Large \hat 2 = \hat 3 = \hat 6 = \hat 7 \)
مثال 2: فرض کنید خطوط \( \Large a \) و \( \Large b \) با هم موازیند. اندازه \( \Large x \) و \( \Large y \) را بدست آورید.

حل 2:
مشاهده میکنیم که \( \Large x \) و \( \Large y \) هر دو زاویههای تند ایجاد شده از برخورد خطوط موازی و مورب هستند، پس:
\( \Large x = y \)
از طرفی با توجه به مکمل بودن \( \Large y \) و زاویه °120 میتوان نوشت:
\( \Large y + 120 = 180° \)
\( \Large → y = 180° – 120° = 60° \)
پس هر دو مجهول \( \Large x \) و \( \Large y \) برابر با °60 خواهند بود.
چند نکته مهم از توازی و تعامد
نکته 1: «دو خط عمود بر یک خط با هم موازیند.»
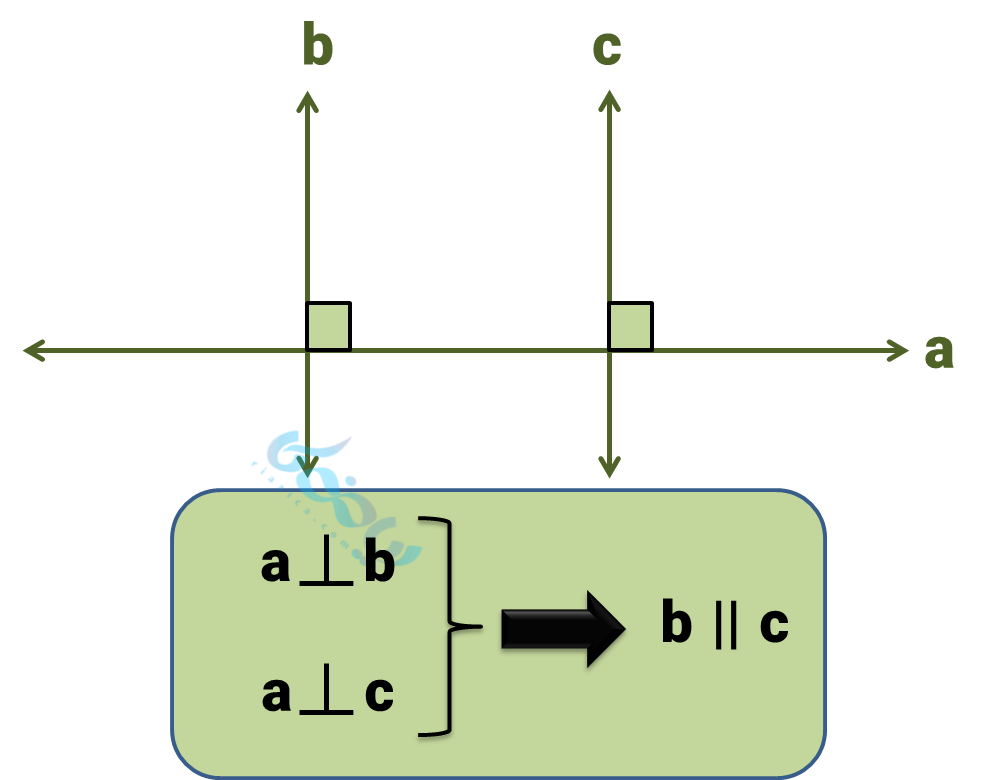
دلیل این موضوع آن است که خط \( \Large a \) روی خطوط \( \Large b \) و \( \Large c \) زوایای مساوی (قائمه) ایجاد کرده. پس طبق قضیه خطوط موازی و مورب این دو خط موازیند.
نکته 2: «دو خط موازی با یک خط با هم موازیند.»
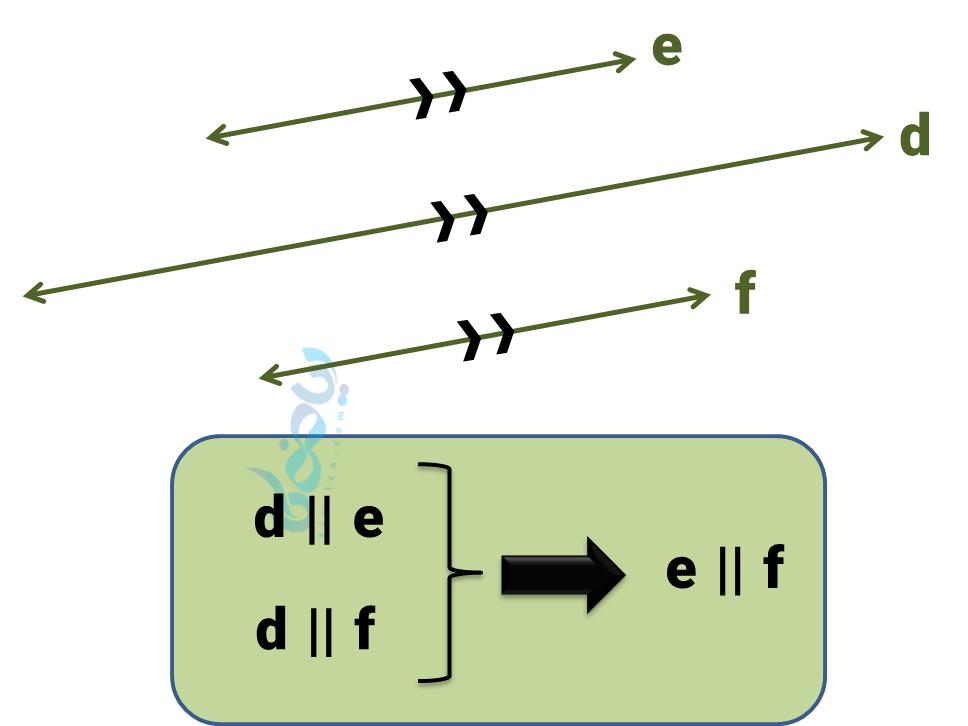
نکته 3: «اگر خطی بر یکی از دو خط موازی عمود باشد، بر خط دیگر هم عمود است.»
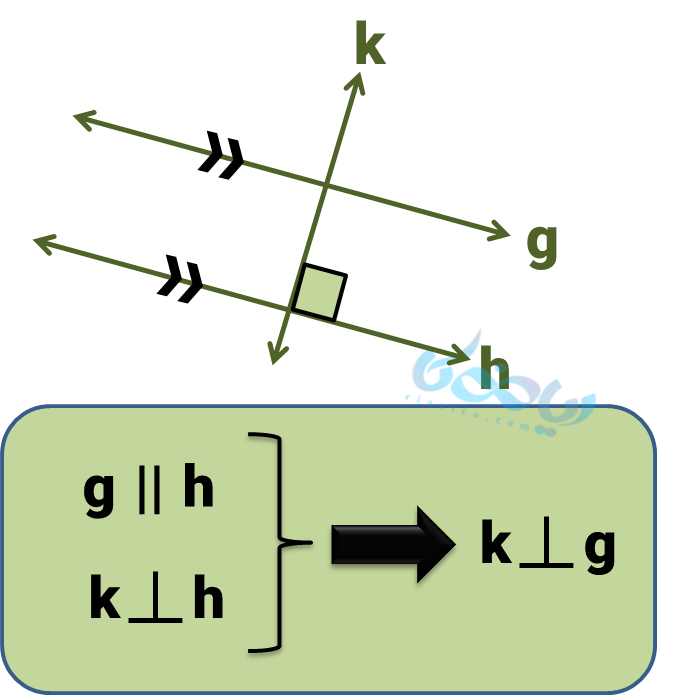
این نکته هم از قضیه خطوط موازی و مورب نتیجه میشود. از آنجا که زاویهای که خط \( \Large k \) روی خط \( \Large h \) ایجاد کرده باید برابر با زاویه روی خط \( \Large g \) باشد، پس آن زاویه هم قائمه خواهد بود.
روش رسم خطی موازی با خط دیگر
اگر خطی مانند \( \Large a \) داشته باشیم و بخواهیم یک خط موازی با آن رسم کنیم، کافی است از «نکته 1» استفاده کنیم: (دو خط عمود بر یک خط با هم موازیند).
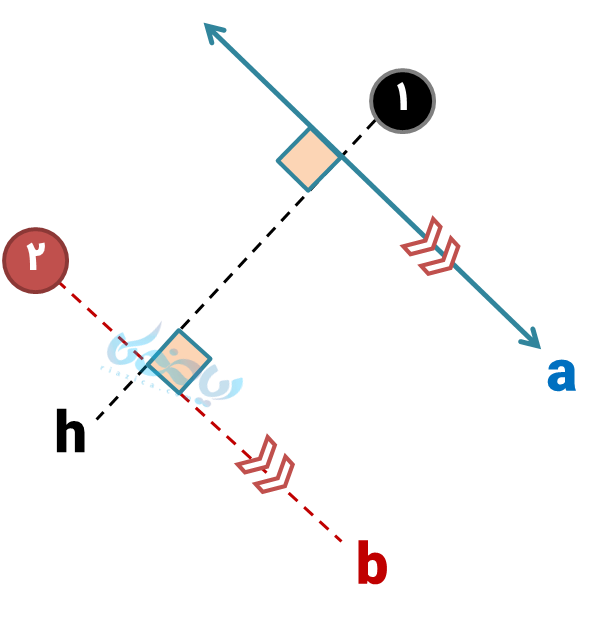
بنابراین در مرحله (1) خطی عمود بر خط \( \Large a \) رسم میکنیم (\( \Large h \)) و در مرحله (2) با رسم خطی عمود بر خط \( \Large h \)، موفق شدهایم خطی موازی با خط اول رسم کنیم.
مثال ترکیبی با مبحث چهارضلعیها
مثال 3: با توجه به خطوط موازی و مورب ، ویژگی زوایا در متوازیالاضلاع را بنویسید.
حل 3:
میدانیم که در متوازیالاضلاع، اضلاع روبرو موازیند. بنابراین میتوانیم آن را همچون شکل زیر بصورت چهار خط که دو به دو با هم موازی هستند، نشان دهیم. زوایای داخلی و خارجی متوازیالاضلاع با اعداد 1 تا 4 برای هر رأس نمایش داده شده است.
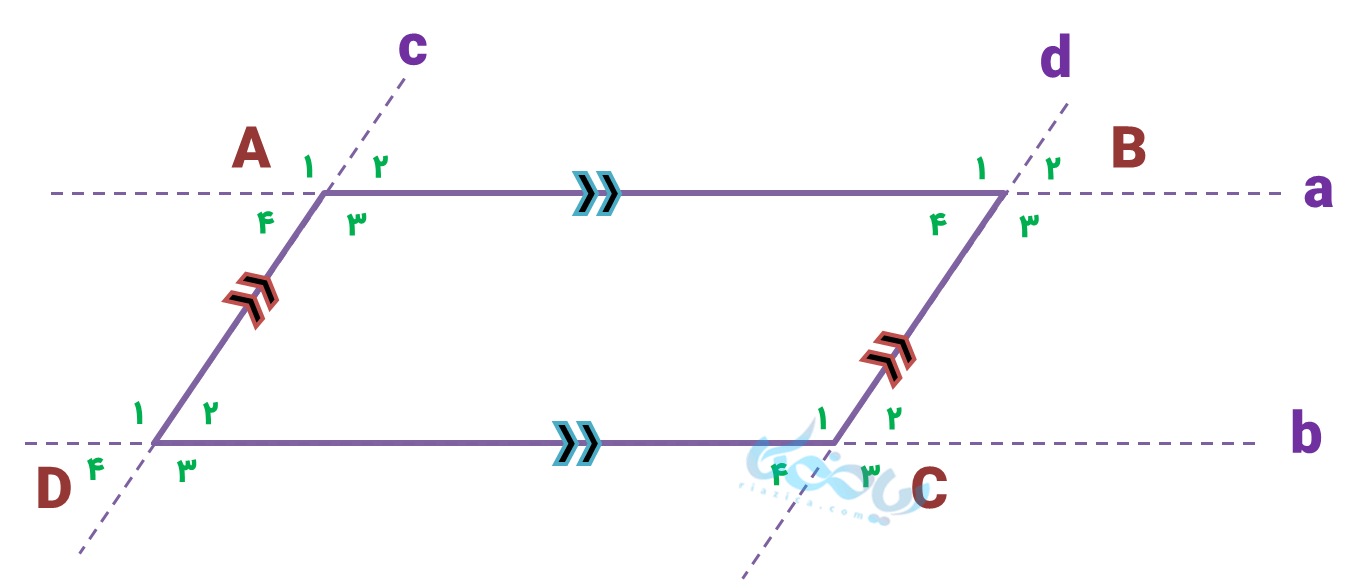
(خطوط \( \Large a \) و \( \Large b \) موازی – خط \( \Large c \) مورب):
(برابری زاویههای باز) \( \Large \hat {A_1} = \hat {A_3} = \hat {D_1} = \hat {D_3} \)
(برابری زاویههای تند) \( \Large \hat {A_2} = \hat {A_4} = \hat {D_2} = \hat {D_4} \) (*)
از طرفی زوایای \( \Large \hat {D_1} \) و \( \Large \hat {D_2} \) مکمل یکدیگرند، پس:
\( \Large \hat {D_1} + \hat {D_2} = 180° \)
حال از برابری زاویههای باز، به جای \( \Large \hat {D_1} \)، معادل آن یعنی \( \Large \hat {A_3} \) را در این تساوی جایگذاری میکنیم:
\( \Large \hat {A_3} + \hat {D_2} = 180° \)
این رابطه نشان میدهد که در متوازیالاضلاع زوایای مجاور مکملاند.
(خطوط \( \Large c \) و \( \Large d \) موازی – خط \( \Large a \) مورب):
(برابری زاویههای باز) \( \Large \hat {A_1} = \hat {A_3} = \hat {B_1} = \hat {B_3} \)
(برابری زاویههای تند) \( \Large \hat {A_2} = \hat {A_4} = \hat {B_2} = \hat {B_4} \) (**)
رابطههای (*) و (**) را کنار هم بنویسیم:
\( \Large \hat {A_2} = \hat {A_4} = \hat {D_2} = \hat {D_4} \) (*)
\( \Large \hat {A_2} = \hat {A_4} = \hat {B_2} = \hat {B_4} \) (**)
\( \Large → \hat {D_2} = \hat {B_4} \)
این رابطه نشان میدهد که در متوازیالاضلاع زوایای روبرو با هم برابرند.
لازم به ذکر است که این ویژگیها در درس چهارضلعیها بصورت کامل آموزش داده شده است.
مثال ترکیبی با مبحث معادله
مثال 4: با تشکیل معادله، مقدار \( \Large x \) را در شکل زیر بدست آورید.

حل 4:
با توجه به موازی بودن دو خط، میتوانیم از قضیه خطوط موازی و مورب استفاده کنیم. میدانیم در این حالت زاویههای تند با هم و زاویههای باز با هم برابرند. در صورت سؤال، یک زاویه باز و یک زاویه تند داده شده است. از طرفی یاد گرفتیم که زاویه باز با زاویه تند مکمل یکدیگرند. پس میتوان نوشت:
\( \Large x + (3x-220) = 180° \)
حال مراحل حل معادله درجه اول را گام به گام انجام میدهیم:
\( \Large x + 3x=180 – (-220) \)
\( \Large 4x = 400 \)
\( \LARGE x = \frac {400}{4} = 100° \)
در ادامه مبحث چهار ضلعی ها را مطالعه کنید
زنگ آخر کلاس خطوط موازی و مورب
در این محتوا مفاهیمی همچون خطوط موازی، خطوط متقاطع و خطوط عمود بر هم را مرور کرده و سپس قضیه مربوط به خطوط موازی و مورب را آموختیم. شما قطعاً با این قضیه در دروس ریاضیات و هندسه پایههای مختلف مواجه خواهید شد. معمولاً سؤالات این موضوع، خارج از مثالهایی که در طول درس با هم حل کردیم، نیست. کافی است آنها را مرور کرده و تمرین کنید!
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاهها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی هشتم به شما پیشنهاد میدهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!





واقعا عالی بود، مرسی ???️?
من این مبحث رو بکلی یاد گرفتم
با سلام وادب
خوشحالم که برای شما مفید بوده
سلام خیلی عالی و خوب بود
خدا خیرتون بدهد
باز هم از این مطالب بزارین خیلی مفید هستش
با سلام وادب
دوست عزیز ما پایه هفتتم و هشتم ونهم ودهم رو به طور کامل گفتیم
واقعا عالی و آموزنده بود مرسی
خواهش میکنم
عالی بود??
با سلام ودرود ممنون از نظر لطف شما
باورم نمیشه منی که هیچی بلد نبودم الان فولم
با سلام وادب
خدا رو شکر
با سلام و احترام و خسته نباشید
میخواستم بگم که عالیییی بودن
مچکرم از کمکتون
با سلام ممنون از لطف شما
سلام ممنون واقعا عالی بود من کامل یاد گرفتم بازم ممنون
سلام دوست عزیز
خدا رو شکر ممنون از انرژیی که به ما میدهید
سلام خسته نباشید
a بر b عمود باشد.
b بر c عمود باشد.
انگاه …
لطفا جواب بدید.
با سلام وادب
aبا c موازی است دو خط عمود بر یک خط بر هم موازی هستن
خوب بود
عالی
عالییی بود ممنونم
خطوط موازی و مورب رعد و برقی رو هم بگذارید متشکرم
با سلام همه آموزشها کتاب ریاضی هشتم گذاشته شده از منوی بالای سایت برید آموزشهای پایه هشتم رو ببینید