آموزش ریاضی پایه هفتم
معادله ریاضی هفتم Ⓜ️🥇 – معادله رو ساده کن!
در درسنامۀ معادله ریاضی هفتم ابتدا توضیح میدهیم که معادله چیست. سپس روش حل آن را بیان میکنیم. پیشنهاد میکنیم حتماً قبل از مطالعۀ این درسنامه، درسنامههای عبارتهای جبری و مقدار عددی یک عبارت جبری را مرور کنید. با مطالعۀ این درسنامه و حل مثالهای آن، بر مبحث معادله ریاضی هفتم به راحتی مسلط خواهید شد. با ما تا انتهای درسنامه همراه باشید.
معادله چیست؟
به یک تساوی که دو طرف آن، عبارتهای جبری باشد، معادله میگویند. مثلاً هر یک از عبارتهای زیر، معادله هستند:
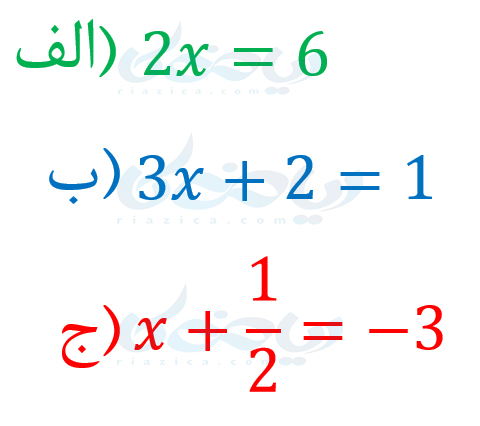
همانطور که در درسنامۀ مقدار عددی یک عبارت جبری گفتیم، میتوان به جای متغیرهای عبارتهای جبری، اعداد را جا گذاری کرد. برای معادلات نیز میتوانیم این کار را به یک شرط انجام دهیم. شرط ما بر قرار ماندن تساوی است. مثلاً معادلۀ “الف” را که در بالا نوشتیم در نظر بگیرید. اگر به جای \(\Large x\)، عدد \(\Large 3\) را قرار دهیم، داریم:
\(\LARGE 2\times 3=6\)
همانطور که میبینید تساوی عددی برقرار است. اما اگر به جای \(\Large x\)، عدد \(\Large 4\) را قرار دهیم، داریم:
\(\LARGE 2\times 4\neq 6\)
به عبارت دیگر، حاصل \(\Large 2\times 4\) برابر با \(\Large 8\) میشود، نه \(\Large 6\). بنابراین تساوی عددی برقرار نیست. اصطلاحاً میگوییم \(\Large 3\) پاسخ معادلۀ \(\Large 2\times 3=6\) است. روش به دست آورن پاسخ یک معادله را حل آن معادله میگوییم. در قسمت بعدی از درسنامۀ معادله ریاضی هفتم به روش حل معادله میپردازیم.
روش حل معادله ریاضی هفتم
میتوانیم پاسخ یک معادله را با سعی و خطا به دست آوریم. مثلاً معادلۀ \(\Large 2x+1=7\) را در نظر بگیرید. اگر از یک شروع کرده و اعداد طبیعی را امتحان کنیم، خواهیم دید که عدد \(\Large 3\) پاسخ این معادله است. اما این روش اصلاً مناسب نیست. اولاً لزوماً پاسخ یک معادله، عدد طبیعی یا صحیح نیست. ثانیاً هیچ تضمینی وجود ندارد که در تلاشهای اولیه به جواب برسیم. همۀ اینها به کنار، در آینده با معادلاتی روبه رو میشویم که حتی در اعداد حقیقی پاسخی ندارند. بنابراین به دنبال روشی هستیم که با طی کردن تعدادی گام مشخص (نه با سعی و خطا) به پاسخ برسیم. در قسمت بعدی از درسنامۀ معادله ریاضی هفتم ابتدا یک مطلب مهم را در مورد تساویها توضیح داده و سپس روش حل معادله را بیان میکنیم.
جمع دو طرف تساوی با یک عدد
اگر دو طرف یک تساوی را با یک عدد جمع کنیم، چه اتفاقی میافتد؟ آیا باز هم تساوی برقرار است؟ مثلاً تساوی زیر را در نظر بگیرید:

اگر دو طرف تساوی را با یک عدد صحیح مثبت مثل \(\Large 3\) جمع کنیم، آنگاه خواهیم داشت:

تساوی بالا درست است. زیرا \(\Large 4+3\) در دو طرف تساوی برابر با \(\Large 7\) میشود. اگر دو طرف تساوی را با یک عدد صحیح منفی مثل \(\Large -5\) جمع کنیم چه طور؟ باز هم تساوی برقرار است؟ این کار را انجام میدهیم:

باز هم تساوی برقرار است. زیرا دو طرف تساوی برابر با \(\Large -1\) میشود. جمع کردن با اعداد گویا و یا به طور کلی اعداد حقیقی نیز، اشکالی ایجاد نمیکند. مثلاً میتوانیم دو طرف تساوی را با عدد \(\Large \frac{3}{8}\) جمع کنیم:
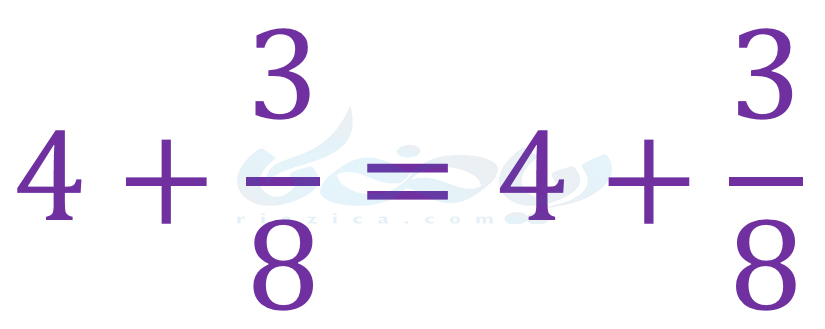
تساوی برقرار است چون دو طرف آن برابر با \(\Large \frac{35}{8}\) است. حتی ضرب دو طرف تساوی در یک عدد حقیقی نیز مشکلی به وجود نمیآورد. در قسمت بعدی از درسنامۀ معادله ریاضی هفتم به این موضوع میپردازیم.
ضرب دو طرف تساوی در یک عدد
همۀ کارهایی که در قسمت قبل برای جمع انجام دادیم، برای ضرب نیز میتوانیم انجام دهیم. مثل قبل، تساوی \(\Large 4=4\) را در نظر بگیرید. اگر دو طرف تساوی را در یک عدد صحیح مثبت مثل \(\Large 3\) ضرب کنیم، آنگاه خواهیم داشت:

تساوی بالا درست است. زیرا \(\Large 4\times 3\) در دو طرف تساوی برابر با \(\Large 12\) میشود. اگر دو طرف تساوی را در یک عدد صحیح منفی مثل \(\Large -5\) ضرب کنیم چه طور؟ باز هم تساوی برقرار است؟ این کار را انجام میدهیم:

باز هم تساوی برقرار است. زیرا دو طرف تساوی برابر با \(\Large -20\) میشود. ضرب کردن در اعداد گویا و یا به طور کلی اعداد حقیقی نیز، اشکالی ایجاد نمیکند. مثلاً میتوانیم دو طرف تساوی را در عدد \(\Large \frac{3}{8}\) ضرب کنیم:
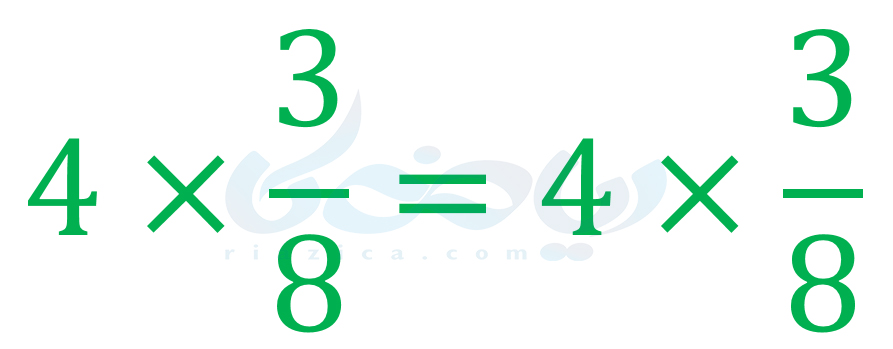
تساوی برقرار است چون دو طرف آن برابر با \(\Large \frac{3}{2}\) است. بنابراین میتوانیم دو طرف یک تساوی را با یک عدد حقیقی جمع و یا در یک عدد حقیقی ضرب کنیم. با توجه به این مطلب، در قسمت بعدی از درسنامۀ معادله ریاضی هفتم، به روش حل معادله میپردازیم.
حل معادله
فرض کنید معادلۀ زیر را به ما داده و از ما خواستهاند که پاسخ معادله را پیدا کنیم.

همانطور که گفتیم باید سعی کنیم معادله را طوری ساده کنیم تا یک طرف تساوی عدد باقی بماند و یک طرف دیگر متغیر. بنابراین سعی میکنیم کاری کنیم تا در سمت راست تساوی بالا عدد باقی بماند و در سمت چپ متغیر (البته میتوانستیم این کار را به صورت برعکس نیز انجام دهیم. یعنی متغیر را سمت راست نگه داریم و عدد را سمت چپ). بنابراین عدد \(\Large -4\) را که قرینۀ \(\Large 4\) است در دو طرف تساوی جمع میکنیم تا عدد \(\Large 4\) در سمت چپ از بین برود:

معادله به صورت زیر در میآید:

حالا دو طرف را در وارون ضریب \(\Large x\) که همان \(\Large \frac{1}{3}\) است ضرب میکنیم تا \(\Large x\) تنها شود:
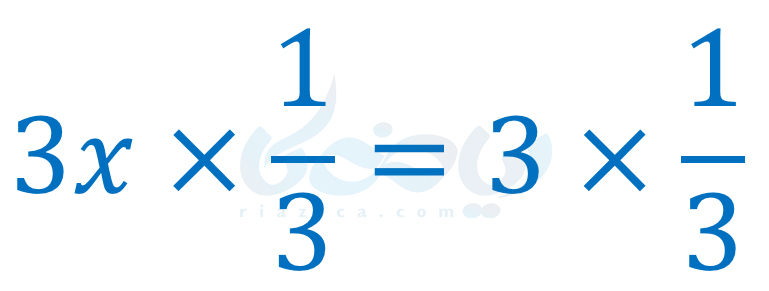
معادله به صورت ساده شدۀ زیر در میآید:

دیدید به چه سادگی و بدون سعی و خطا، پاسخ معادله را یافتیم. به طور کلی برای حل هر معادله باید معادله را تا جایی ساده کنیم که یک طرف تساوی، متغیر و طرف دیگر تساوی عدد باشد. در قمست بعدی از درسنامۀ معادله ریاضی هفتم ، مثالهای متنوعی از معادله حل خواهیم کرد تا کوچکترین مشکلی در این مبحث نداشته باشید.
مثالهایی از حل معادله ریاضی هفتم
مثال 1 معادله ریاضی هفتم: معادلۀ \(\Large 2x-5=x\) را حل کنید.
حل: سعی میکنیم معادله را طوری ساده کنیم تا در سمت چپ آن، متغیر باقی بماند و در سمت راست آن، عدد (البته همانطور که گفتیم میتوانید این کار را برعکس انجام دهید. یعنی متغیر را در سمت چپ و عدد را در سمت راست نگه داریم). با توجه به اینکه دنبال یافتن پاسخ معادله در مجموعۀ اعداد حقیقی هستیم، با متغیرِ این معادله نیز میتوانیم مانند یک عدد حقیقی رفتار کنیم. یعنی میتوانیم \(\Large -x\) را با دو طرف تساوی جمع کنیم:
\(\Large 2x-5+(-x)=x+(-x)\)
\(\LARGE \Rightarrow x-5=0\)
حال کافی است دو طرف معادله را با \(\Large 5\) جمع کنیم:
\(\LARGE x-5+5=0+5\)
\(\LARGE \Rightarrow x=5\)
به مثال بعدی از درسنامۀ معادله ریاضی هفتم دقت کنید.
مثال 2 معادله ریاضی هفتم: معادلۀ \(\Large 4x+1=2x+3\) را حل کنید.
حل: سعی میکنیم معادله را طوری ساده کنیم تا در سمت چپ آن، متغیر باقی بماند و در سمت راست آن، عدد (البته باز هم همانطور که گفتیم میتوانید این کار را برعکس انجام دهید. یعنی متغیر را در سمت چپ و عدد را در سمت راست نگه داریم). ابتدا \(\Large -2x\) را با دو طرف تساوی جمع کنیم:
\(\Large 4x+1-2x=2x+3-2x\)
\(\LARGE \Rightarrow 2x+1=3\)
حال \(\Large -1\) را با دو طرف تساوی جمع میکنیم:
\(\LARGE 2x+1-1=3-1\)
\(\LARGE \Rightarrow 2x=2\)
در گام آخر، دو طرف تساوی را در \(\Large \frac{1}{2}\) ضرب میکنیم:
\(\LARGE 2x \times \frac{1}{2}=2 \times \frac{1}{2}\)
\(\LARGE \Rightarrow x=1\)
مثالهایی دیگر از حل معادله ریاضی هفتم
مثال 3 معادله ریاضی هفتم: معادلۀ \(\Large 3x-4=4x-3\) را حل کنید.
حل: سعی میکنیم معادله را طوری ساده کنیم تا در سمت چپ آن، عدد باقی بماند و در سمت راست آن، متغیر (البته همانطور که گفتیم میتوانید این کار را برعکس انجام دهید. یعنی متغیر را در سمت چپ و عدد را در سمت راست نگه داریم). بنابراین، ابتدا \(\Large -3x\) را با دو طرف تساوی جمع کنیم:
\(\Large 3x-4-3x=4x-3-3x\)
\(\LARGE \Rightarrow -4=x-3\)
حال \(\Large 3\) را با دو طرف تساوی جمع میکنیم:
\(\LARGE -4+3=x-3+3\)
\(\LARGE \Rightarrow -1=x\)
به مثال بعدی از درسنامۀ معادله ریاضی هفتم دقت کنید.
مثال 4 معادله ریاضی هفتم: معادلۀ \(\Large 2-3x=5x+1\) را حل کنید.
حل: سعی میکنیم معادله را طوری ساده کنیم تا در سمت چپ آن، عدد باقی بماند و در سمت راست آن، متغیر (باز هم همانطور که گفتیم میتوانید این کار را برعکس انجام دهید. یعنی متغیر را در سمت چپ و عدد را در سمت راست نگه داریم). ابتدا \(\Large 3x\) را با دو طرف تساوی جمع کنیم:
\(\Large 2-3x+3x=5x+1+3x\)
\(\LARGE \Rightarrow 2=8x+1\)
حال \(\Large -1\) را با دو طرف تساوی جمع میکنیم:
\(\LARGE 2-1=8x+1-1\)
\(\LARGE \Rightarrow 1=8x\)
در گام آخر، دو طرف تساوی را در \(\Large \frac{1}{8}\) ضرب میکنیم:
\(\LARGE 1 \times \frac{1}{8}= 8x \times \frac{1}{8}\)
\(\LARGE \Rightarrow \frac{1}{8}=x\)
نکته :بعضی از همکاران برای تنها کردن متغیر به جای اینکه دوطرف را با عدد یا متغیر قرینه جمع کنند متغیرهای اضافه را در حالت جمع وتفریق به طرف دیگر میبرند وعلامتش را قرینه می کنند ودر آخر طرفین را به ضریب متغیر تقسیم میکنند ما این روش را در پست حل معادله درجه اول هشتم کاملا توضیح دادهایم.
ویدیویی از آموزش معادله ریاضی هفتم
در این ویدیو سعی کردیم که آموزشی کامل از حل معادله ریاضی هفتم را برای شما عزیزان بیان کنیم.
زنگ آخر کلاس معادله ریاضی هفتم
همانطور که گفتیم، به یک تساوی که دو طرف آن عبارت جبری باشد، معادله میگوییم. دیدیم که برای یافتن پاسخ معادلات میتوان عبارات جبری یا اعداد را به دو طرف تساوی اضافه و یا در دو طرف تساوی ضرب کرد. در مثالهای مختلفی که حل کردیم، معادله را طوری ساده کردیم که یک طرف آن متغیر و طرف دیگر آن اعداد باشد. به این صورت توانستیم پاسخ معادلات را بیابیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث معادله ریاضی هفتم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





چطور یک ضلع را به دست آوریم
سلام و عرض ادب
چه شکلی در مسئله ضلعش خواسته شده و چه اطلاعاتی در مورد مسئله داده شده منظورم این است که آیا ۴۵ محیط یا مساحت مسئله است؟
موفق باشید.
????
چطور یک ضلع را به دست آوریم مثال گفته ضلع xرا به دست آورید وطرف دیگه داده ۴۵ گفته ضلع ایکس را به دست آورید
سلام و عرض ادب
چه شکلی در مسئله ضلعش خواسته شده و چه اطلاعاتی در مورد مسئله داده شده منظورم این است که آیا ۴۵ محیط یا مساحت مسئله است؟
موفق باشید.
۳
بستگی ب شکل دارع ک شکلش چی باشع
هاییییی😂🤣
با سلام وادب
ممنون
به سختی
سلام من توی عادله اشکال دارم از خیلی ها هم پرسیدم ولی هیچی رو ازش متوجه نشدم اگه میشه به صورت خیلی آسان توضیح بدین که متوجه بشم
ممنون?
شما اول عبارتهای جبری رو خوب یاد بگیرید
سلام آقای موسوی ما باید چجوری تعریف معادله پایه هفتم را داشته باشیم
با سلام وادب
تعریف داخل پست هست استفاده کنید
جبری را میشود به ما توضیح دهی
با سلام وادب
منظورتون از جبری چی هست؟
خیلی عالی ومفید
ممنون از دیدگاه شما
من هم همینطور زیاد متوجه نشدم ?
با سلام وعرض ادب
ممنون میشم با راهنماییتون و بیان نکات قوت و ضعف این پست ما را در بهتر کردن آن یاری فرمایید.
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
باید مفهومی بخونی عزیز
با سلام وعرض ادبممنون از پاسخگ.یی شما
سلام میشه بگید چجوری تومعادله وقتی در جمع اعداد عدد کسری با عدد صحیح بود چیکار کنیم
سلام دوست عزیز اگه عد صحیح باشه که با توجه به علامت اعداد اونها رو با هم جمع میکنیم اعداد یکطرف معادله متغیرها یه طرف وآخر سر طرف معلوم تقسیم بر ضریب مجهول
اما اکه عددکسری بود ابتدا دو طرف معادله رو در مخرج کسر ضرب میکنیم تا معادله از حالت کسری در بیاد وبعد حل میکنیم
برای شرکت در کلاس خصوصی به صورت آنلاین با شماره تلفن ۰۹۱۲۸۱۴۸۹۷۵ تماس بگیرید
سلام من توی عادله اشکال دارم از خیلی ها هم پرسیدم ولی هیچی رو ازش متوجه نشدم اگه میشه به صورت خیلی آسان توضیح بدین که متوجه بشم
ممنون?
سلام https://riazica.com/algebraic-expressions/ این پست رو هم بخونید
سلام میشه فصل 4 ریاضی هفتم رو برام توضیح بدین
سلام و عرض ادب
https://riazica.com/relationship-between-line-segments/
بفرمایید.
سلام اگه میشه میتوانی این سوال رو حل کنید=(۲_)+(۳÷(۱۱_۳)_۷)× ۴این یک مساله می خام اگه بفرستی از روش سوال های دیگر رو حل کنم ممنون میشم
با سلام ما جواب موردی به این صورت نمیدیم
سلام واقعا عالیه من همیشه مطالعه میکنم
ومیخونم چون خیلی ریاضی دوست دارم
ممنونم
با سلام وادب
خیلی خوب وعالیه انشالله موفق باشید ریاضیات واقعا شیرین ودوست داشتنی هست
سلام من توی معادله اشکال دارم از خیلی ها هم پرسیدم ولی هیچی رو ازش متوجه نشدم اگه میشه به صورت خیلی آسان توضیح بدین که متوجه بشم
ممنون?
جواب داده شد
چرا جواب من رو نمیفرستی
با سلام
ما این همه مطلب خوب رایگان گذاشتیم که خودتون یاد بگیرید وجواب بدید
مهدی فرامرزی خیلی خوب بود
سلام همین فقد خاستم بگم
معادله یعنی وقتی که دو چیز با هم برابرند
و علامت مساوی دارند مثل
X + 2 =6
اگه میشه معادله رو خیلی آسان توضیح بدین خیلی ها رام توضیح دادن اما من متوجه نشدم
سلام وعرض ادب
در پست کامل توضیح دادیم کافیه ایکس رو تنها کنید چه جور؟اگه با ایکس عددی جمع شده برعکس دوطرف رواز اون عدد کم کنید واگر کم شده دوطرف رو با ایکس جمع کنید وقتی ایکس تنها شد دو طرف رو به ضریب ایکس تقسیم کنید
استاد شما خیلی پیچوندید ، بصورت ساده اینطوریه که معلوم ها یک طرف مجهول ها یک طرف بعدشم طرف معلوم تقسیم بر ضریب مجهول یعنی
2x+4=6
2x=6-4 (وقتی 4 میره اونور منفی میشه)
2x=2
X=2÷2 , X=1
با سلام وادب
دوست عزیز اینی که شما میگوید وکاملا درسته نتیجه ای هست که از مطالب ما گرفته میشه در ریاضی همه مطالب با دلیل پیراهن باید گفته بشه
خوب بود
عالی
با سلام وادب
ممنون از نظر شما
سلام
ببین عزیزم شما
4x+1=2x+3
رو در نظر بگیر..
اول از همه
4xو2xرو بیار سمت راست
و اعداد رو ببر چپ بعد
جمعشونو انجام بده
و عدد ایکس رو با عدد بدون متغیر تقسیم کن
عدد به دست اومده جواب ایکس میشه
با سلام
ممنون از پاسخگویی شما
خیلی خوبه
ممنون دوست عزیز
سلام واقعا عالی بود ازتون ممنونم ?
سلام و عرض ادب
ممنون از توجهی که داشتید.
موفق باشید.
برای حل معادله چ کرد
سلام جواب x2+7-1 چه میشه لطفا
سلام دوست عزیز
این یک عبارت جبری میباشد نه معادله پس جوابی ندارد وفقط میشود به ازای مقادیر مختلف مقدار آن را به دست آورد
این معادله را بایستی مساوی صفر قرار داد، بعد اعداد بدون متغیر را به سمت راست انتقال داد که میشود ۶- و بعد طرف معلوم تقسیم بر ضریب مجهول و جواب میشود ۳-
سلام دوست عزیز
ممنون از پاسخگویی شما
ببخشید مثلا جواب 5x=-20 چه میشود؟
سلام و عرض ادب
جواب میشود ۴- .
موفق باشید.
سلام و عرض ادب
40=(2+x)5
یا سلام دوست عزیز
کافیه ابتدا طرفین رو به ۵ تقسیم کنید وبعپ از ۲ کم کنید جواب میشه ۶
مارو در اینستا یه آدرس زیر دنبال کنید
اشتراکها: هما
با سلام وعرض ادب
خدا رو شکر که براتون مفید بوده
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
من که چیزی نفهمیدم
سلام و وقت بخیر
کدوم بخش رو متوجه نشدید
من در اینستا حل معادله هفتم رو یاد دادم حتما ببینید
ایدی اینسا رو برام بزار
خیلی خیلی ممنون خیلی خوب بود??
با سلام واحترام
خدارو شکر که براتون مفید بوده
سلام عالی بود
با سلام واحترام
سعی ما هم همین بوده
☹️☹️☹️☹️اپلا سوال من این نبود اینو آورد
☹️☹️☹️☹️
سلام و وقت بخیر
سوالتون رو بفرمایید
چگونه این معادله را حل کنیم
لطفا جواب بدید
۲X_۳=X+۵
سلام و عرض ادب
مجهول ها را به سک طرف برده اصطلاحا تنهاشون میکنیم و سپس طرفین را بر ضیب مجهول تقسیم میکنیم.
x=8
یس
اگر میشه خیلی ساده توضیح بدید و مقدمه نداسته باشه
این چیه اخه من سوال میزنم اینو میاره یعنی چیه ?????
با سلام عزیزم
باید خودتون به سوالات امتحان چواب بدید
سلام معادله x+۲ =۶ جوابش چیه
با سلام واحترام
خیلی ساده هست شش منهای چهار میشود دو
سلام معادله x+۲ =۶ جوابش چیه؟؟؟؟
با سلام وعرض ادب
خیای ساده ۶منهای دو مبشود ۴
سلام ۳ایکس-۵=جوابش چی میشه
دوست عزیز معادله به این راحتی حلش رو هم پر پست گفتیم بعد چرا معادله طرف دوم نداره
بسیار عالی با این که هیچی از معادله نمیدونستم، عالی بود ، تونستم به صورت کامل معادله هفتم رو یاد بگیرم
با عرض ادب واحترام
خوشحالیم که براتون مفید بوده معرف ما به دوستانتون باشید
عالی ۱۰۰فصید
با سلام وعرض ادب
ممنون دوست عزیز
سلام
میشه جواب معادله یک دوم ایکس مساوی با ۹ رو بگید؟
سلام واحترام
کافیه دوطرف معادله رو در یک دو ضرب کنی جواب بدست میاد
۱۰+……=_۲۰
-۴-…..=-۸
….+۱۰=-۴-۸
۱۵-=۳x
با سلام وادب
سوالی به این راحتی کافیه طرفین رو به سه تقسیم کنید که جواب میشه منفی پنج
اصلا چیزی ک من میخاستم نبود☹?
با سلام دوست عزیز
میشه بفرمایید دقیقا دنبال چی بودید؟
بسیار عالی و مفید
با سلام ووقت به خیر
هدف ما هم همین هست مختصر ومفید
سلام و عرض ادب
میشه جواب 3n =-27
و جواب
t-1+9t=6t-9
و بگید؟
رو بگید
با سلام و ادب
این پست رو نوشتیم که خودتون معادله رو حل کنید
سلام و عرض ادب
میشه جواب 3(-x+2)-(1+x)
رو بگید؟
باسلام وادب
این یه عبارت جبری هست جواب ندارد
???
میشه جواب
t-1+9t=6t-9
بگید
مجهولها رو ببر یکطرفرو مجهولها هم یک طرف وحل کن
نفهمیدم اصلا
میشه جوابو بگید شاید اونجوری بفهمم
سلام
جواب 3x_6 =15
رو میشه بگید
با سلام
پست رو بخونید وسعی کنید خودتون حل کنید خیلی ساده هست
سلام وقت بخیر
در آخرین مثال معادله یک هشتم از کجا آمده؟؟ ممنون میشم جواب بدید
با سلام واحترام
چون میخواهیم ضریب ایکس که هشت هست از بین ببریم دوطرف رو در معکوسش یک هشتم ضرب میکنیم
خیلی چرت?به دردذ نخور?
با سلام
کجاش به درد شما نخورد؟
سلام ببخشید میشه یه توضیح کلی از معادله بدید؟
سلام ببخشید میشه یه توضیح کلی از معادله بدید؟
میشه لطفا جواب بدید
معادله در واقع یه تساوی هست که در اون یک مجهول داریم که باید مقدار اون مجهول رو بدست بیاریم
سلام ببخشید میشه چند نمونه معادله به صورت کامل توضیح دهید؟
ممنون میشم اگر جواب بدید
با سلام
دوست عزیز در اینجا مقدور نیست تماس بگیرید تا به صورت خصوصی براتون گفته بشه
عالی بود ممنون
با سلام واحترام
ممنون از نگاه وانرژی شما
میشه چند تا معادله سخت بگید که ایکس یک طرف تساوی باشه
یعنی فقط یک ایکس وجود داشته باشد
جوابش رو هم بگید عالی میشه
عالی
خیلی خوب بود ممنون از شما
ممنون از نگاه شما
منفی سه ایکس + ایکس
حاصل این عبارت چی هست؟
با سلام
منفی دو ایکس
کاش آسون تر میگفتین
با سلام
دیگه آسونتر از این ؟
سلا ببخشید چجوری میشه معادله ی 4x=-20 رو به دست بیارم فردا امتحان دارم
با سلام وادب
کافیه ۲۰ رو به چهار تقسیم کنید به اصطلاح طرف معلوم تفسیم بر ضریب مجهول
راستش من برای تمرین معادله اومدم ولی پس از دیدن نظرات و حل کردن این معادلات توسط اساتید ، حل معادله من از این رو به اون رو شد ، واقعا ممنون☺️??
با سلام وادب
خرسندیم که تاثیر گذار بودیم
ببخشید ولی ایراد من هنوز رفع نشده میخواستم بدونم اگه فقط حاصل جمع و ضرب سه تا مجهول را داشته باشیم چطوری جواب را پیدا کنیم
با سلام دوست عزیز
به روش جایگذاری میشه حل کرد
سلام این سایت عالی است.
لطفا عبارت جبری را هم در این سایت آموزش دهید
با سلام دوست عزیز
در بین آموزش های سایت هست
خوبه من یاد گرفتم
با سلام وادب
خدا روشکر
سلام خسته نباشید انشاءالله
چگونه معادله ای که جوابی به آن داده نشده را حل کنیم چند مثال بزنید تا خوب متوجه بشوم
😊
با سلام وادب
دوست عزیز من منظور شما رو کتوجه نمیشم اگه حل معادله منظور شماست که در این درسنامه مفصل توضیح دادیم با مثال بعد اگه منظ.ورتون معادله ای هست که جواب ندارد
معادلاتی که مجهول حذف بشه وبه یک تساوی نادرست برسیم جواب ندارند.
یکم ساده تر توضیح بدید لطفا 😵💫😵💫😵💫
سلام دوست عزیز دیگه از این ساده تر نمیشه
سلام اصلا توضیحتون خوب نیست توضیح معادله=اول باید تساوی رو بزاریم بعد ایکس ها سمت چپ عدد ها سمت راست و بعد عدد هارو اگه باید جمع کنم که باهم جمع میکنیم اما اگر باید از هم کم کنیم کم میکنیم و بعد عدد مان را تقسیم بر ایکس مان میکنیم و بعد پاسخ به دست میآید اما اگر دو ایکس داشته باشیم باید از هم کم شأن کنیم و بعدش تقسیم را انجام دهیم.
سلام دوست عزیز این راهی که شما میفرمایید فرموله شده راهی است که ما با دلیل واثبات گفتیم اینقد به این راههای تستی وفرمولی عادت کردیم که راه درست رو اشتباه میدانید
سلام ببخشید یه معادله هست برای تیز هوشان میگه ۵ خط کسری x+1 مساوی با ۴ خط کسری 2x
چطوری معادله رو باید حساب کرد
با سلام دوست عزیز
کافیه از خاصیت طرفین وسطین استفاده کنید دوتا کسر رو به صورت ضربدری در هم ضرب کنید و حاصل هر ضرب رو در یک طرف تساوی بنویسید تا به یک معادله ساده تبدیل بشه وبعد حل کنی
سلام …چطور به عنوان یک معلم معادله رو در بحث ورود به تدریس به دانش آموز میفهمونید ؟
سلام همکار گرامی اولا فیلم آموزشی پایان این مقاله رو ببینید ثانیا من اول با جای خالی که برای بچه ها آشناست چند تا مثال میزنم بعد میگم حالا به جای جای خالی از حروف انگلیسی استفاده میکنیم با مثالهای متعدد بچه ها راحت یاد میگیرن از مثالهای ساده به سخت بروید