آموزش ریاضی پایه هشتم
شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
هم نهشت یعنی همون کپی برابر اصل! کپی که بچرخونی، ببری جای دیگه یا جلوی آینه قرار بگیره باز هم برابر اصله! در این درس مهم از مجموعه آموزش ریاضی پایه هشتم ، شکل های هم نهشت معرفی شده و انواع تبدیلهای هندسی که به کمک آن هم نهشتی را تشخیص میدهیم، بیان میگردد. همچنین با ذکر نکتهای در مورد برابری اجزای متناظر در این نوع شکلها و حل چند مثال خواهیم توانست به سادگی از آن در آینده استفاده کنیم.
شکل های هم نهشت
در ریاضی پایه هفتم تا حدودی با شکل های هم نهشت آشنا شدیم و دیدیم که شکلهای هم نهشت کاملاً مساوی هستند. در ریاضی پایه هشتم ابتدا تعریف و خاصیت این شکلها بیان شده و سپس به موضوع مهم مثلث های هم نهشت خواهیم رسید.
بیایید ابتدا با تعریف آشنا شویم!
اگر بتوانیم شکلی را با یک یا چند تبدیل هندسی (تقارن، دوران و انتقال) طوری بر شکل دیگر منطبق کنیم که کاملاً یکدیگر را بپوشانند، می توانیم بگوییم که این دو شکل با یکدیگر هم نهشت هستند. (همان کپی برابر اصل!)
نکته: هم نهشتی را با علامت \( \Large ≅ \) نشان میدهند؛ به عنوان مثال هم نهشتی دو چهارضلعی \( \Large ABCD \) و \( \Large EFGH \) را نشان میدهند:
\( \LARGE ABCD ≅ EFGH \)
انواع تبدیلهای هندسی
برای جابجا کردن یا چرخاندن یک شکل در صفحه (بدون تغییر اصل شکل و تبدیل آنها به شکل های هم نهشت) چند راه وجود دارد که به آنها تبدیل هندسی میگویند:
- انتقال: جابجایی یک شکل به کمک یک بردار از نقطهای به نقطه دیگر (تمام شکل بدون تغییر یا چرخش عیناً به محل دیگری منتقل میشود)؛
- دوران: چرخاندن شکل حول یک نقطه به اندازه زاویه دلخواه (تمام شکل بدون تغییر همزمان اطراف یک نقطه میچرخند- فرض کنید یک میله از شکل به نقطه وصل شده و شکل را چرخاندهایم)؛
- تقارن: قرینه شدن شکل نسبت به یک خط، پاره خط، محور و … (آن خط مانند آینه عمل میکند).
در هر سه مورد نشان داده شده در شکل زیر دو شکل هم نهشت نشان داده شده است و در هر کدام این تبدیلهای هندسی قابل مشاهدهاند:
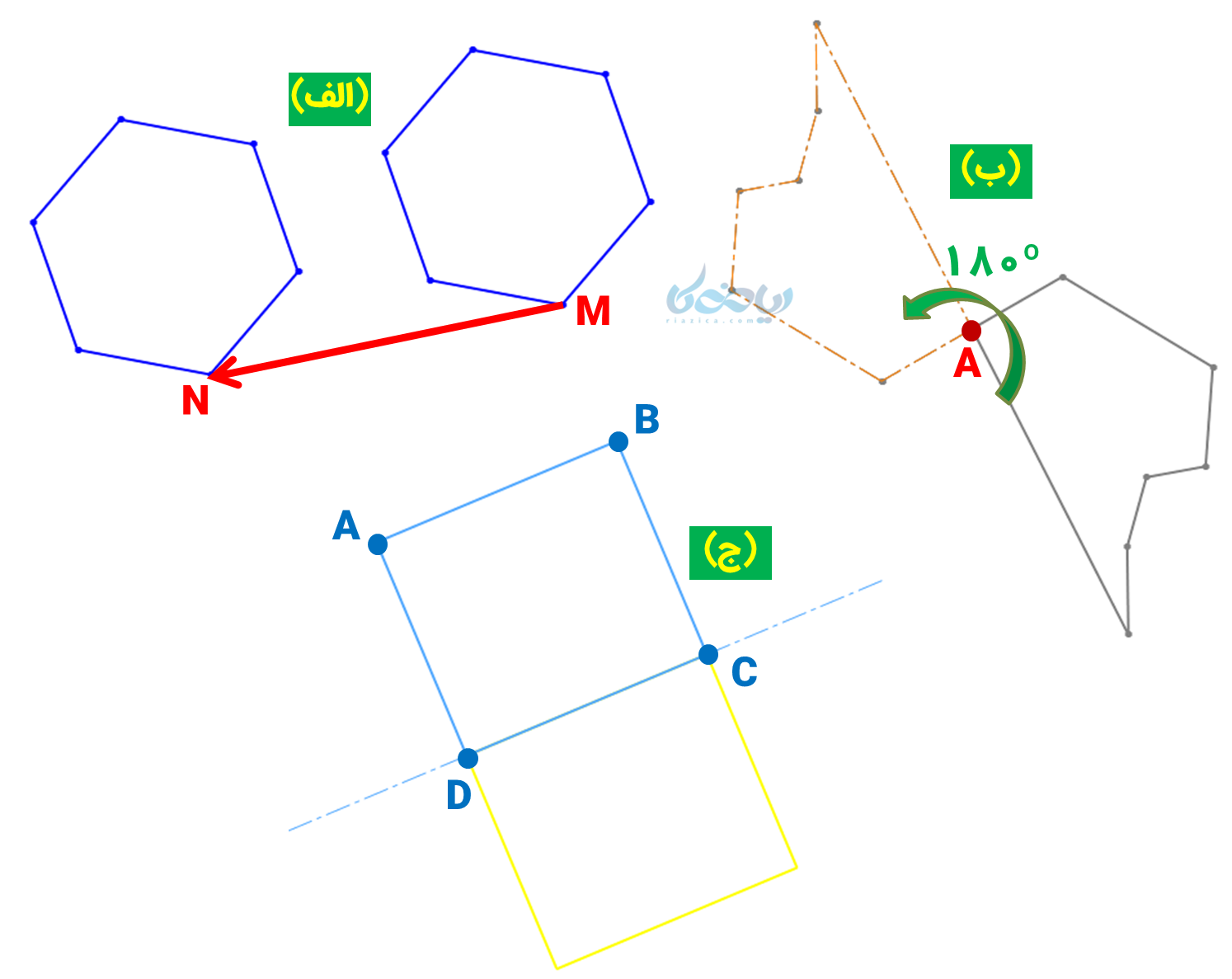
موارد (الف)، (ب) و (ج) به ترتیب نشاندهنده انتقال، دوران و تقارن شکلها هستند. مطابق شکل بالا، ششضلعی منتظم (الف) توسط بردار \( \Large \overrightarrow {MN} \) منتقل شده است. هفتضلعی (ب) حول نقطه A به اندازه 180 درجه دوران کرده و مربع (ج) نسبت به ضلع CD خود تقارن یافته است.
نکته مهم از شکل های هم نهشت: اگر ضلعهای دو چندضلعی (غیر از مثلث) دو به دو با هم برابر باشند نمیتوان گفت قطعاً هم نهشت اند. اما اگر ضلعهای دو مثلث دو به دو برابر باشند، آن دو مثلثهای هم نهشت هستند.
به عنوان نمونه، در دو چهارضلعی زیر ضلعها دو به دو مساویند، اما به وضوح مشخص است که هم نهشت نیستند (یکی مستطیل و دیگری متوازی الاضلاع!)
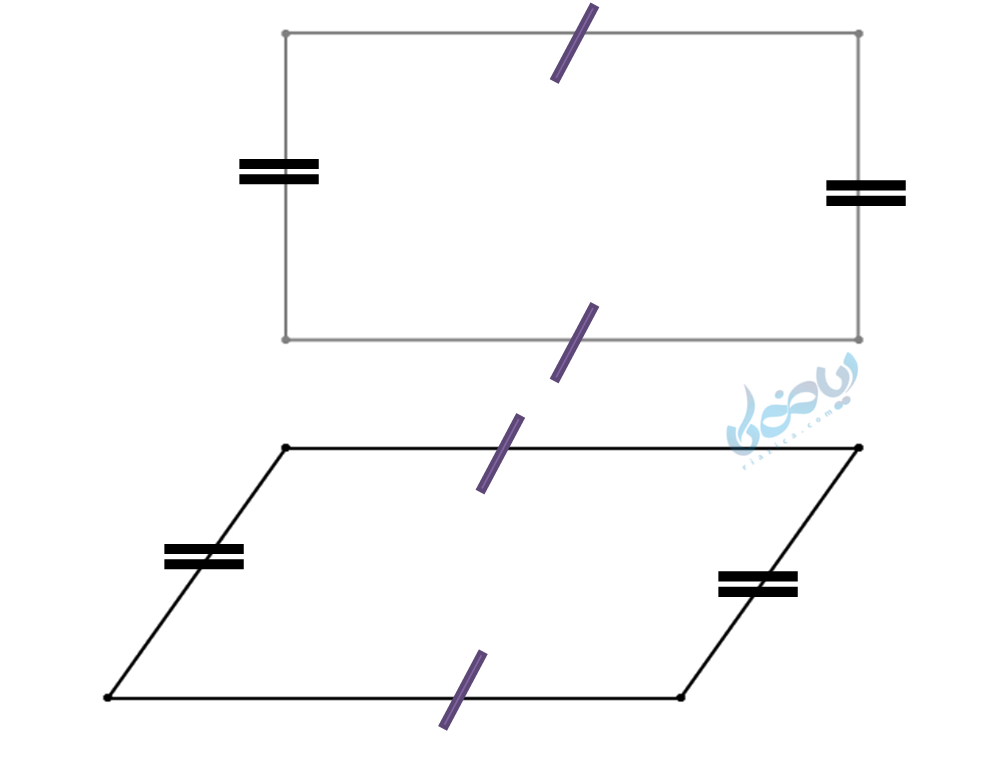
ویژگی شکل های هم نهشت
اجزای متناظر دو شکل هم نهشت (یعنی زاویهها و ضلعهای متناظر) با هم برابرند. به عنوان مثال دو چهارضلعی زیر هم نهشت هستند و زاویهها و ضلعهای متناظر آنها برابرند.
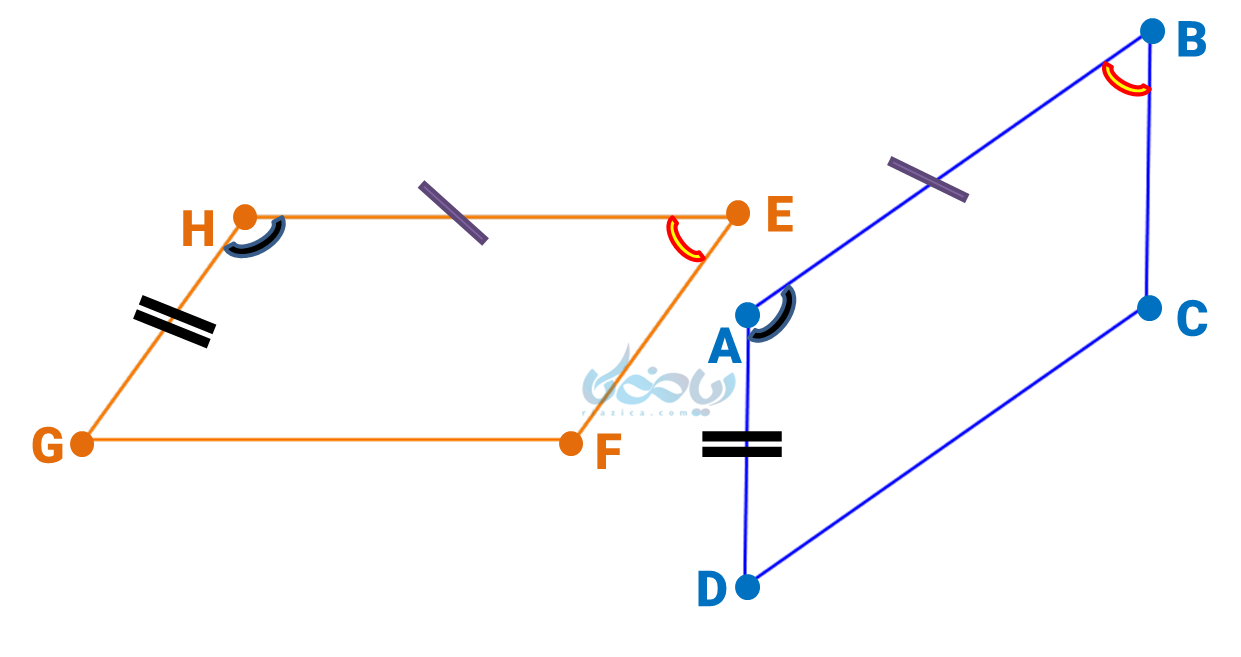
یعنی زاویه \( \Large \hat H \) با زاویه \( \Large \hat A \) ، زاویه \( \Large \hat E \) با زاویه \( \Large \hat B \) ، ضلع \( \Large \overline{GH}\) با ضلع \( \Large \overline{AD} \) و ضلع \( \Large \overline{HE}\) با ضلع \( \Large \overline{AB} \) برابرند.
اگر دو شکل را با هم مطابقت دهید، دیگر برابریها را نیز میتوان چنین نوشت:
\( \Large \hat G = \hat D \)
\( \Large \hat F = \hat C \)
\( \Large \overline{FG} = \overline{CD} \)
\( \Large \overline{EF} = \overline{BC} \)
مثالهایی کامل از شکل های هم نهشت
مثال 1: در دو چهارضلعی هم نهشت زیر، نوع انتقال را مشخص کرده و سپس \( \Large x \) ، \( \Large y \) و \( \Large z \) را بدست آورید.
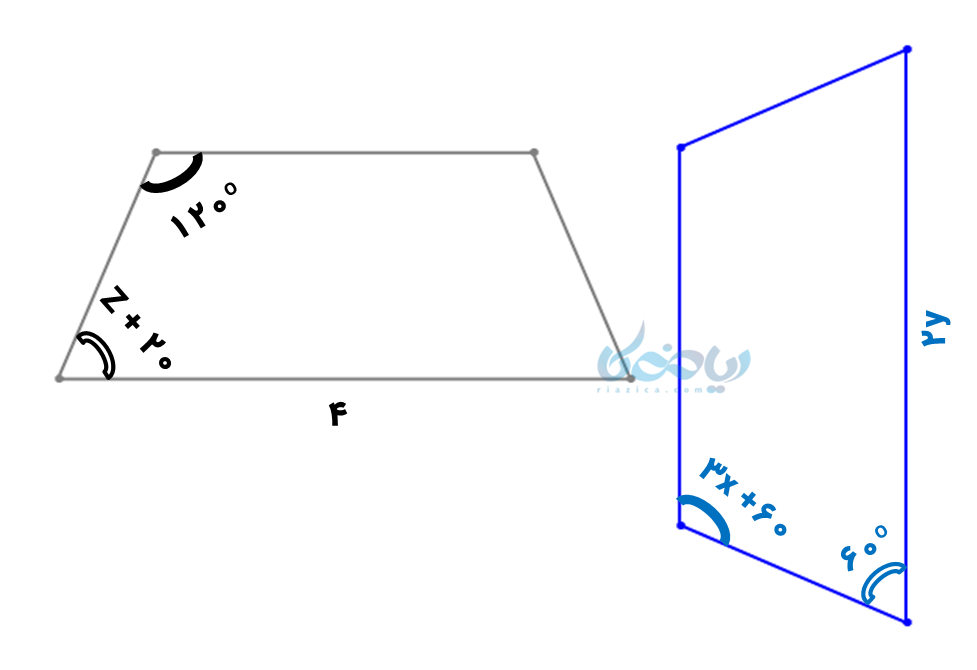
حل 1:
با توجه به شکل مشخص است که چهارضلعی سمت چپ به اندازه 90 درجه در جهت عقربههای ساعت چرخیده است؛ بنابراین نوع انتقال، دوران است.
برای محاسبه مجهولات مسأله از این نکته استفاده میکنیم که در شکل های هم نهشت زاویهها و ضلعهای متناظر برابرند. جهت سهولت حل مسئله اضلاع و زوایا، آنها را نامگذاری کردهایم:
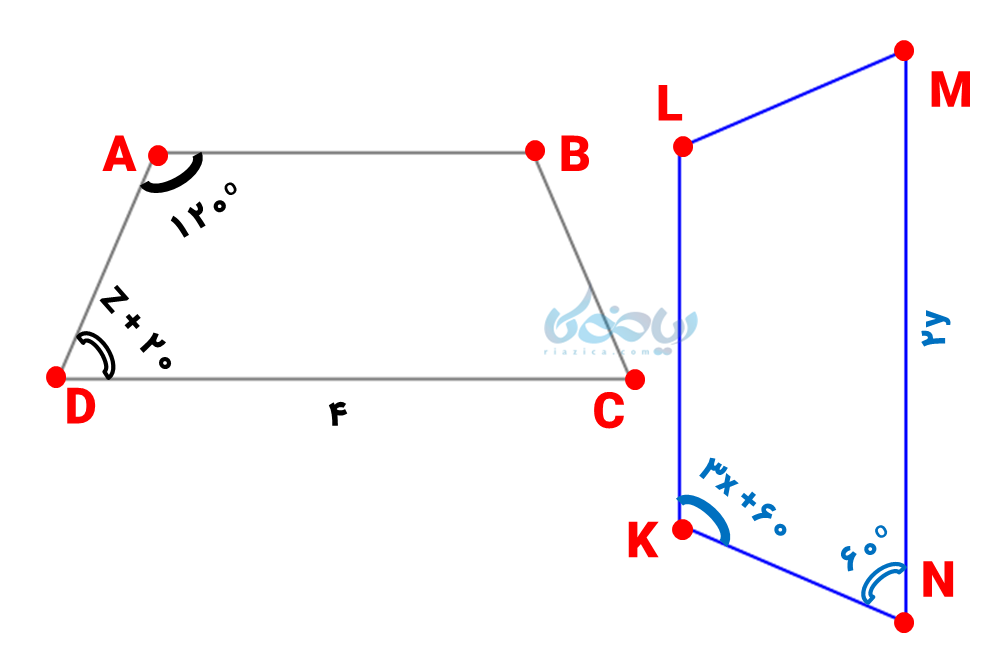
در این دو شکل، زاویه \( \Large \hat A \) با \( \Large \hat K \) ، زاویه \( \Large \hat D \) با \( \Large \hat N \) و ضلع \( \Large \overline{CD} \) و \( \Large \overline{MN} \) برابرند پس میتوانیم مجهولات را بدست آوریم:
\( \Large ABCD ≅ KLMN \)
\( \Large \hat A = \hat K → 120° = 3x+60 \)
\( \Large → 3x = 120-60=60 \)
\( \Large → x = 20° \)
\( \Large \hat D = \hat N → z+20 = 60° \)
\( \Large → z = 60-20=40° \)
\( \Large \overline{CD} = \overline{MN} → 4 = 2y \)
\( \Large y= \frac {4}{2} = 2 \)
نمونهای از مثلثهای هم نهشت
مثال 2: دو مثلث هم نهشت زیر با چه تبدیل هندسی بر یکدیگر منطبق میشوند؟ مقادیر \( \Large x \) و \( \Large y \) را بدست آورید.
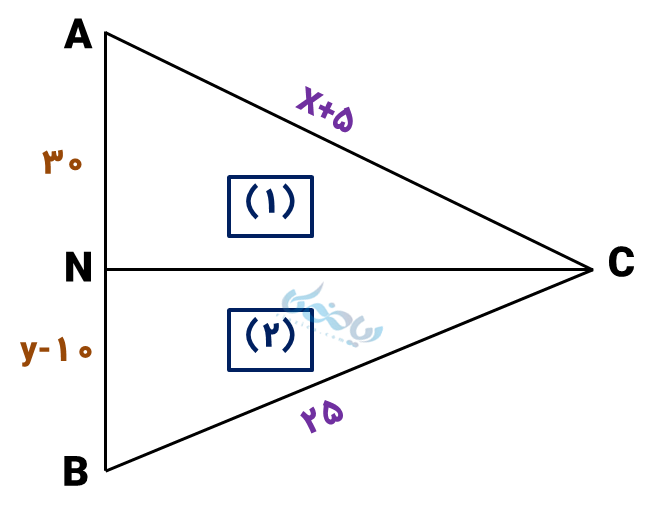
حل 2:
اگر به دو مثلث توجه کنیم، متوجه خواهیم شد که مثلث (1) با تقارن محوری بر مثلث (2) منطبق شده است. یعنی ضلع \( \Large \overline{NC} \) نقش آینه را بازی کرده است.
از آنجا که شکل های هم نهشت دارای اجزای متناظر برابر هستند، میتوانیم با نوشتن برابریها به شکل زیر مجهولات \( \Large x \) و \( \Large y \) را بدست آوریم:
\( \Large \overline{AN} = \overline{BN} → 30 = y-10 \)
\( \Large y= 30 + 10 = 40 \)
\( \Large \overline{AC} = \overline{BC} → x + 5= 25 \)
\( \Large x= 25 – 5= 20\)
توجه: مثلثهای هم نهشت حالت خاصی از شکل های هم نهشت هستند و از آنجا که از اهمیت زیادی برخوردارند، بحث در مورد آن در درسنامه جداگانهای آموزش داده شده است.
زنگ آخر کلاس شکل های هم نهشت
در این درسنامه یاد گرفتیم که شکل های هم نهشت دقیقاً چیست و فهمیدیم چرا بهش میگیم کپی برابر اصل! با انواع تبدیلهای هندسی آشنا شدیم و نکته مهمی در مورد برابری اجزای متناظر دو شکل هم نهشت آموختیم که با استفاده از آن در مثالها توانستیم مجهولات مسأله را بدست آوریم.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاهها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی هشتم به شما پیشنهاد میدهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!





عالی بود ❤ممنون
سلام من همه مطالب تون دیدم عالی بودن ۲۶تاش خوندم خیلی قشنگ توضیح دادین شما برای درسای دیگه خودتون سایتی دارین مثل همین ریاضیکا یا یه سایتی که مورد پسند تون باشه بهم معرفی کنید چون سایت تای دیگه حتی معلم خودم قشنگ توضیح نمیدن وقتی میخونم گوش میکنم واسم حوصله سر بره ممنون میشم اگه جوابمو بدید
با سلام ودرود
ممنون از نظر لطف شما این مطالب حاصل سی سال تجربه تدریس هست متاسفانه من سایتی نمیشناسم
برای پایه هشتم پکیج ویدیویی درس ریاضی رو هم داریم
عالی بود ?
با سلام دوست عزیز
ممنون از نظر لطف شما
عاللللللللللییییییییییی بوددددددددددد ممممممنننننننننننووووووووووووننننننننن🌹
ممنونم از شما واقعا دستتون درد نکنه مطالبتون برای منه دانش آموز هشتمی خیلی مفهوم بود🌹
عالی هستن ممنون ازاین راهنمای ونکته های مهم این درس رو به ما آموختید ممنون.
با سلام و ادب
ممنون از حمایت شما
سلام ممنون از مطالب خوبتون خیلی خوب بود فقط اگه میشه اون معادله هارو بیشتر توضیح بدید
سلام ممنون از مطالب خوبی که دردسترس دانش آموزان قرار دادید فقط اگه میشه معادله ها ر بیشتر توضیح بدید
باسلام
منظورتون کدوم معادلات هست؟