آموزش ریاضی پایه هشتم
خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
یه جوری جلوی آینه وایسا که فقط نصف خودت رو ببینی؛ قبول داری انگار از وسط تا خوردی؟ آره خودشه، تقارن ! یکی از زیباییهای آفرینش خداوند که کافیه با یه نگاه دقیقتر به طبیعت بگردی و پیداش کنی! در این درس از مجموعه آموزش ریاضی پایه هشتم ، ابتدا با تعریف چندضلعی و همچنین چند ضلعیهای منتظم آشنا شده و خط تقارن و مرکز تقارن را در شکلها بررسی خواهیم کرد.
چند ضلعی ها
چند ضلعی ها یکی از مهمترین شکلهای هندسی هستند. آنها را در دروس مختلف و همچنین در معماریهای ساختمانها، کاشیکاریها و … زیاد مشاهده میکنیم. پیش از رسیدن به موضوع خط تقارن بیایید چند تعریف را در مورد چندضلعیها با هم مرور کنیم:
تعریف چند ضلعی
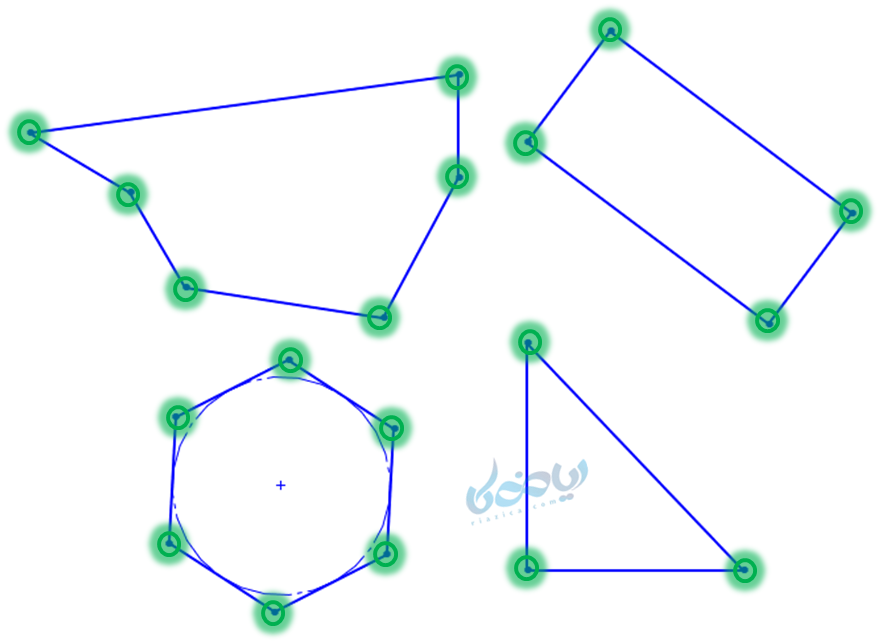
به هر خط شکسته بستهای که ضلعهایش همدیگر را قطع نکنند (به جز در رأسهای آن)، چند ضلعی گفته میشود. به عنوان نمونه، شکلهای زیر چند ضلعی هستند؛ دقت کنید که این خط شکستهها فقط همدیگر را در رأسها (که با رنگ سبز نشان داده شده است) قطع کردهاند:
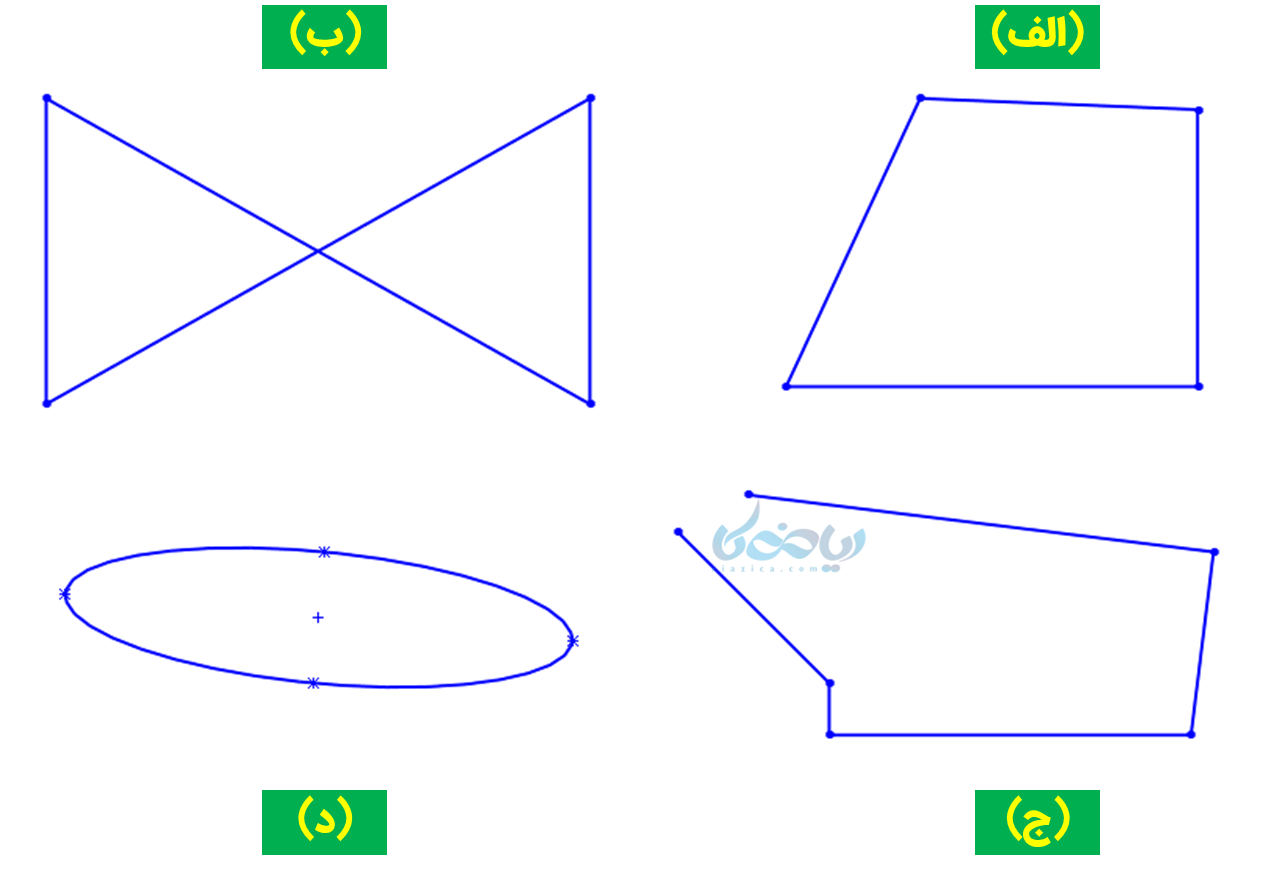
مثال 1: با ذکر دلیل مشخص کنید کدامیک از شکلهای زیر چند ضلعی هستند؟
حل 1:
طبق تعریف به خاطر داشته باشیم که چند ضلعی بودن یک شکل 3 شرط دارد:
- خطشکسته باشد؛
- بسته باشد؛
- خطوط آن همدیگر را قطع نکنند (مگر در رأسها).
شکل (الف) شرایط گفته شده را دارد، پس چند ضلعی است. شکل (ب) چندضلعی نیست، چون خطوط آن همدیگر را در نقطه وسط قطع کردهاند (و این نقطه رأس شکل نیست). شکل (ج) چند ضلعی نیست، چون بسته نیست. شکل (د) هم چند ضلعی نیست، چون با وجود بسته بودن و قطع نکردن، دارای خط شکسته نیست (منحنی است).
تعریف چند ضلعی منتظم
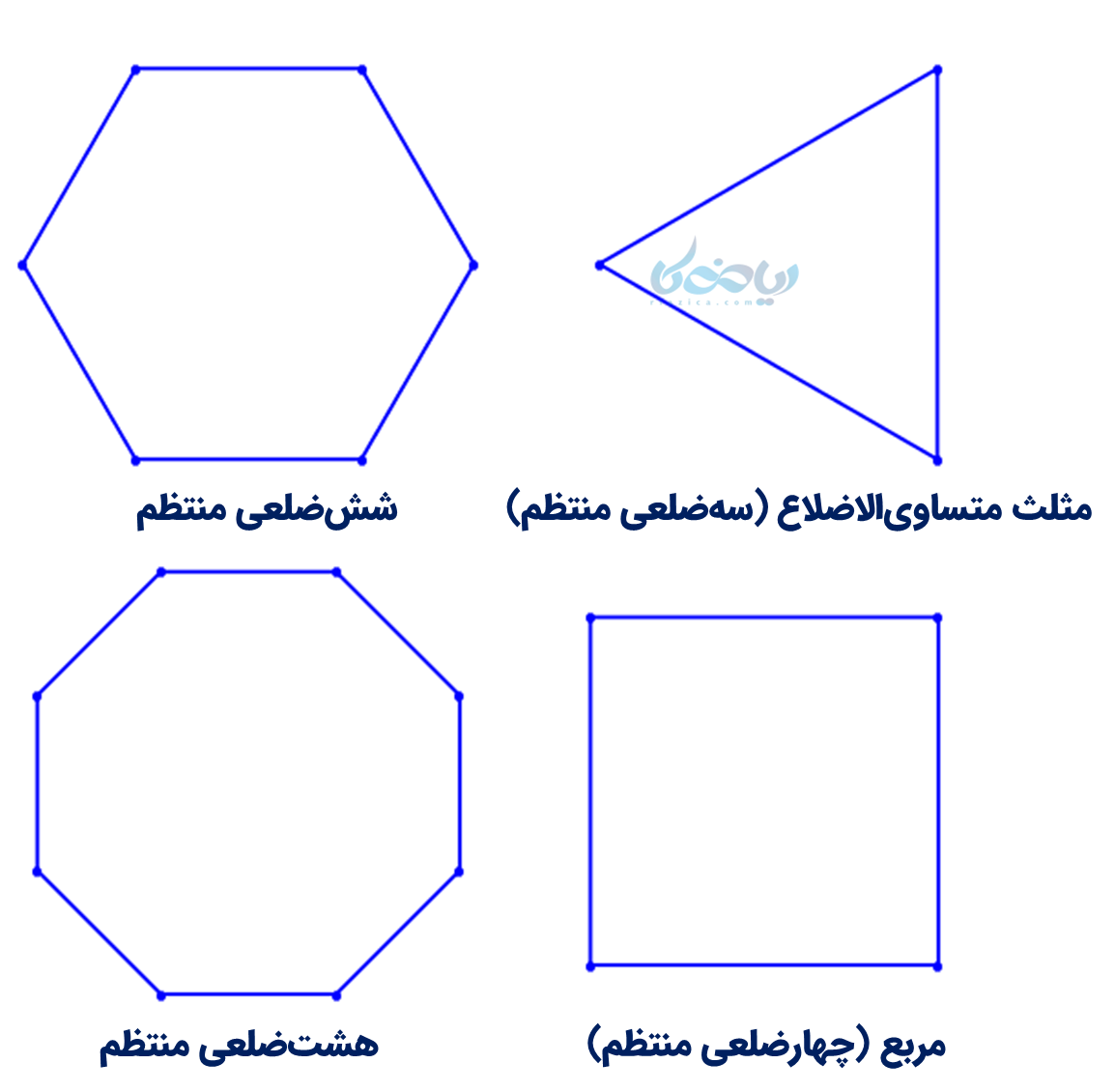
چند ضلعی منتظم به چندضلعی گفته میشود که در آن، همه زاویهها با هم و همه ضلعها با هم برابرند. به عنوان نمونه تعدادی چند ضلعی منتظم را با هم میبینیم:
مثال 2: شکلهای زیر را رسم کرده و مشخص کنید کدامیک چند ضلعی منتظم است.
الف) متوازیالاضلاع؛
ب) لوزی با زاویه قائمه.
حل 2:
الف) متوازیالاضلاع مطابق شکل زیر رسم شده است؛ همانگونه که در درسنامه چهار ضلعیها توضیح داده شده است، در متوازی الاضلاع ضلعهای روبرو موازی و برابرند، اما چهار ضلع و چها زاویه برابر ندارد. پس چهار ضلعی منتظم نخواهد بود.

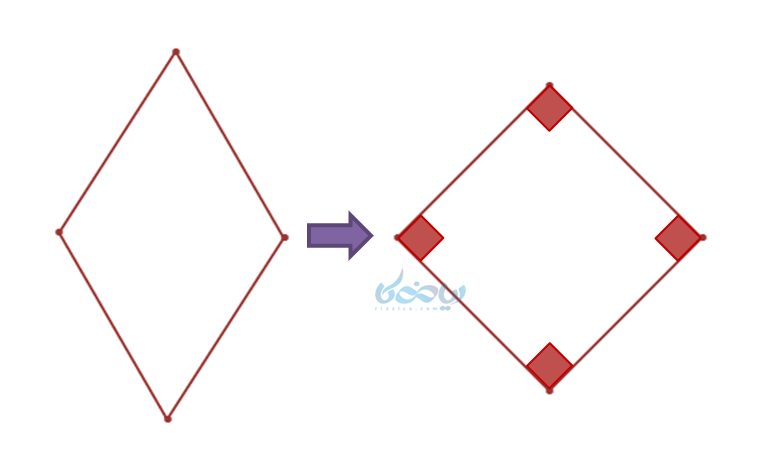
ب) در لوزی هر چهار ضلع برابر و ضلعهای روبرو موازی هستند. اگر زاویههای لوزی را قائمه در نظر بگیریم، تبدیل به مربع میشود که دارای چهار ضلع مساوی و چهار زاویه مساوی (قائمه) بوده و چهار ضلعی منتظم خواهد بود.
خط تقارن چیست؟
خط تقارن (محور تقارن) خطی است که شکل را به دو قسمت مساوی تقسیم میکند و اگر شکل را روی آن تا بزنیم، دو قسمت شکل دقیقاً بر روی هم قرار میگیرند.
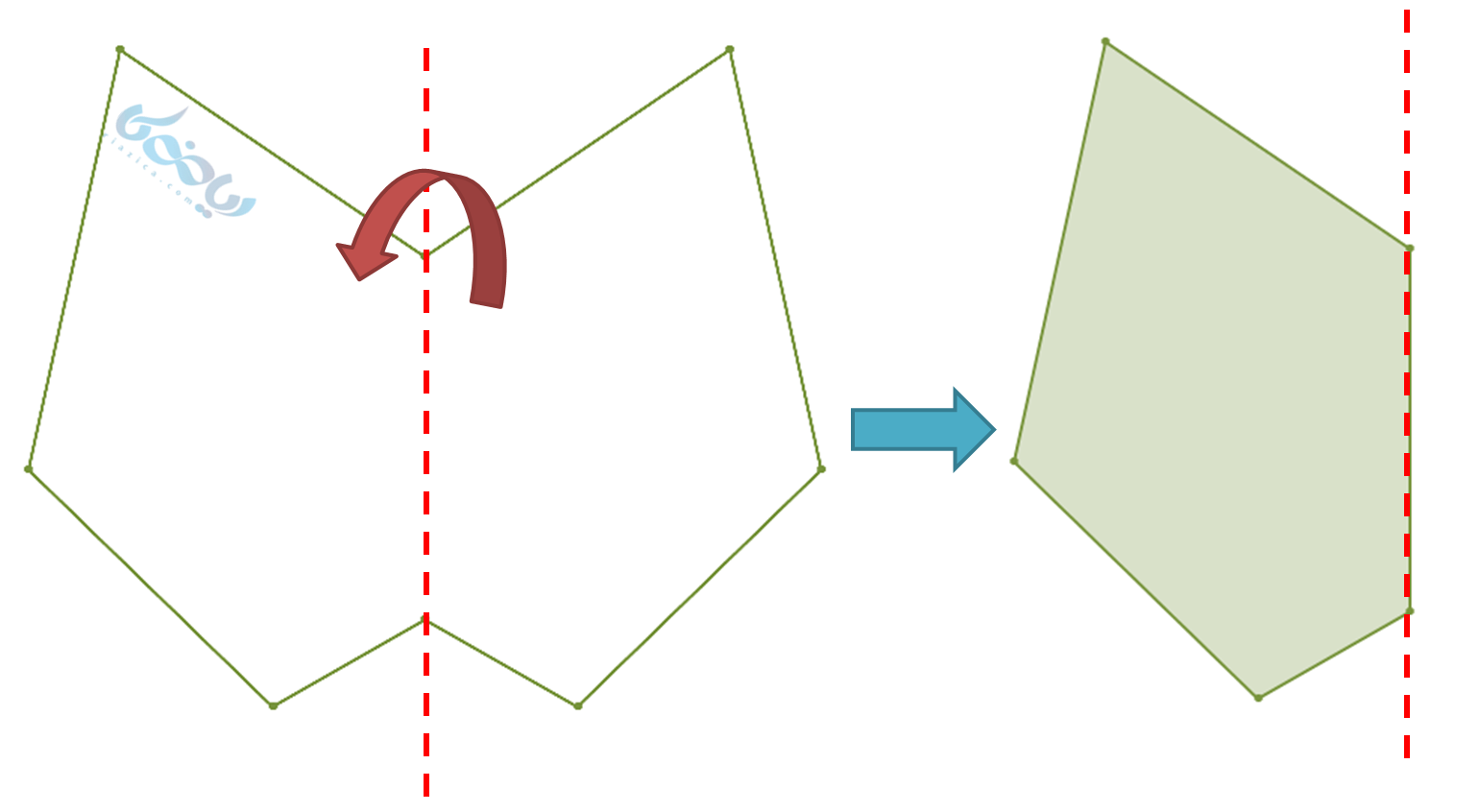
همانطور که میبینیم در هشتضلعی بالا خطچین قرمز خط تقارن شکل است، چون با تا زدن آن سمت راست دقیقاً روی سمت چپ قرار گرفته است. برای جا افتادن مطلب، به مستطیل زیر توجه کنید. بیایید بررسی کنیم که کدامیک از دو خطچین قرمز و آبی رنگ خط تقارن مستطیل است:
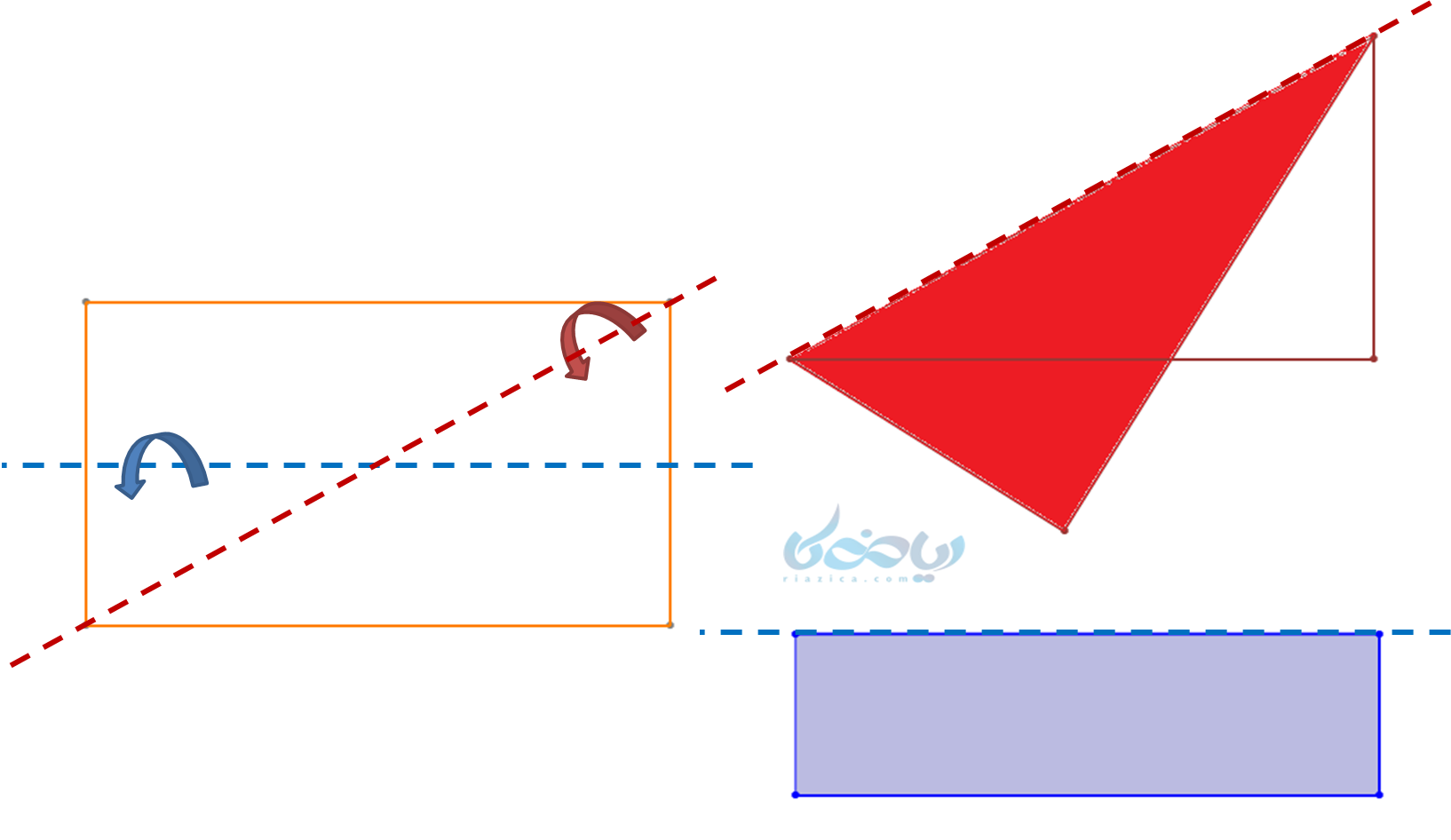
مستطیل را روی این دو خط چین تا میزنیم، مشاهده میکنیم که با خطچین آبی نیمه بالا دقیقاً روی نیمه پایین قرار گرفته است، پس خط چین آبی، خط تقارن مستطیل است. اما با تا زدن مستطیل روی خطچین قرمز، دو طرف شکل روی هم قرار نگرفتهاند، بنابراین خطچین قرمز نمیتواند خط تقارن باشد.
راه تشخیص خط تقارن
در آموزش خط تقارن ریاضی هشتم روشی را یاد خواهیم گرفت که نیازی به تا زدن شکل بر روی خط نداشته باشیم! اگر بخواهیم بدانیم یک خط، خط تقارن شکل هست یا نه، از هر نقطه بر روی محیط شکل، بر خط موردنظر عمودی رسم کرده و به همان اندازه ادامه دهید. اگر آن نقطه روی محیط شکل قرار گرفت خط تقارن است و اگر روی مخیط شکل قرار نگرفت، خط تقارن نیست.
مثال 3: کدامیک از خطوط نشان داده شده در شکل زیر، خط تقارن مثلث است؟
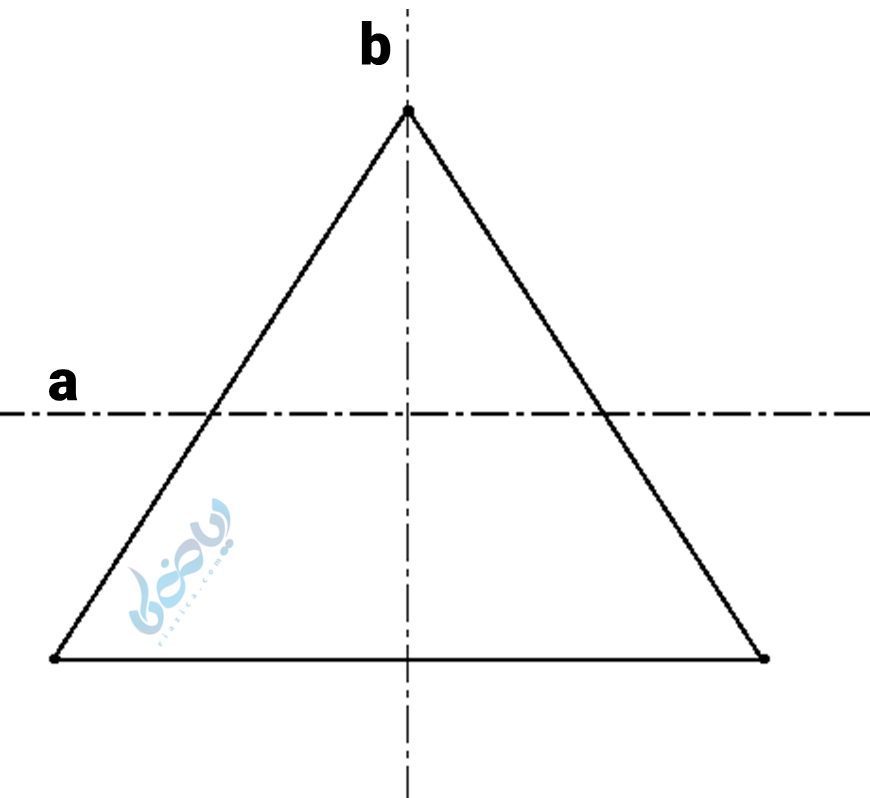
حل 3:
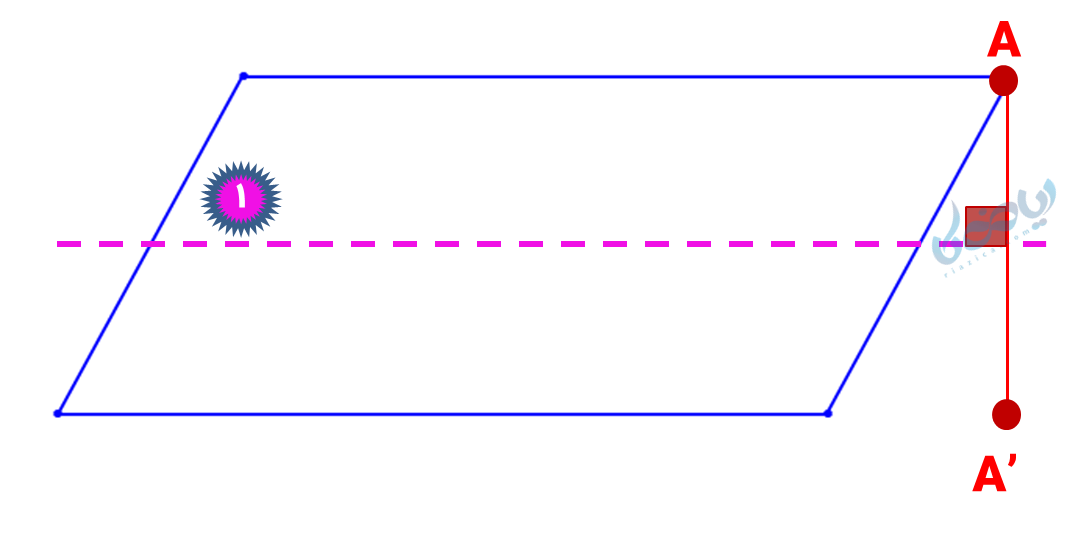
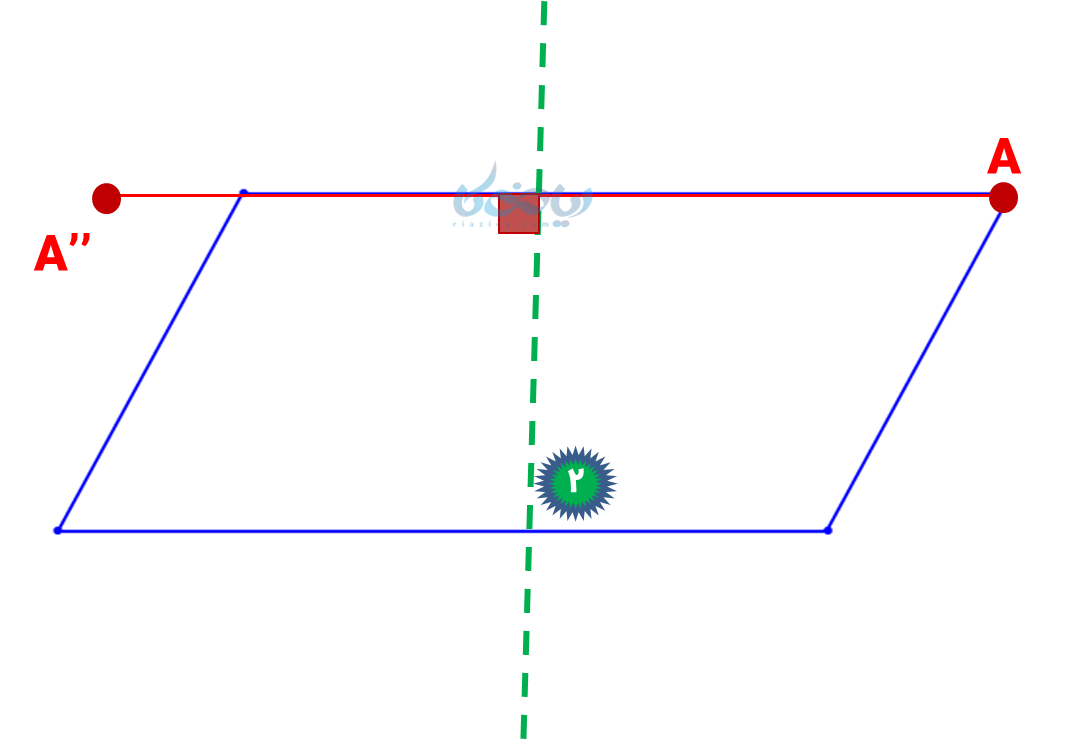
نقطهای مانند \( \Large A \) روی مثلث در نظر گرفتهایم. از این نقطه خطی عمود بر خط \( \Large a \) رسم میکنیم، به اندازه \( \Large A{H_1} \) خط را ادامه میدهیم. نقطه آخر خط را \( \Large A’ \) مینامیم، از آنجا که این نقطه روی مثلث قرار ندارد (داخل قرار گرفته)، خط \( \Large a \) خط تقارن مثلث نیست.
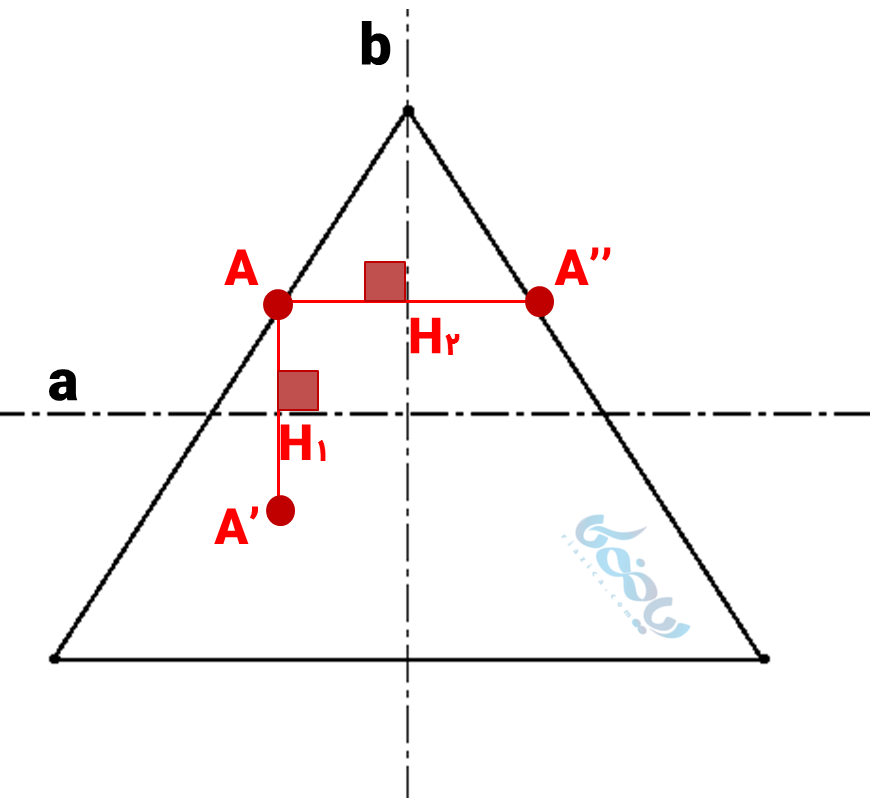
همچنین از نقطه \( \Large A \) خطی عمود بر خط \( \Large b \) رسم میکنیم، به اندازه \( \Large A{H_2} \) خط را ادامه میدهیم. نقطه آخر خط را \( \Large A’’ \) مینامیم، از آنجا که این نقطه روی مثلث قرار گرفته است، پس خط \( \Large b \) خط تقارن مثلث است.
خط تقارن در چند ضلعی منتظم
چند ضلعی منتظم به تعداد اضلاعش، خط تقارن دارد. به عنوان مثال، تعداد محورهای تقارن در پنج ضلعی منتظم 5، مربع 4 و مثلث متساوی الاضلاع 3 است. در شکل زیر، به عنوان نمونه تعدادی چند ضلعی منتظم را مشاهده میکنید:
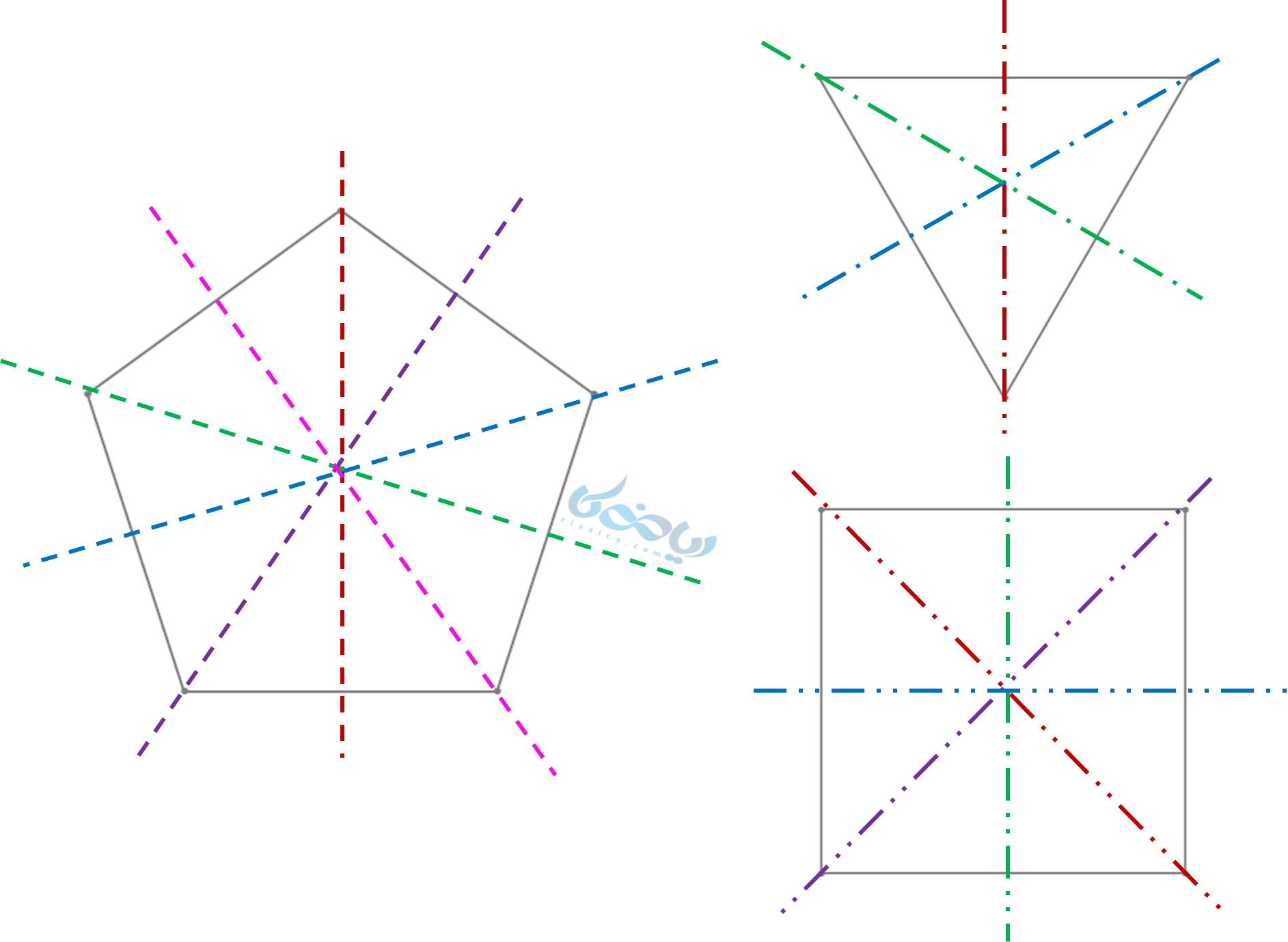
نکته: دایره دارای بینهایت خط تقارن است.
مرکز تقارن
اگر شکلی را حول یک نقطه، ١٨٠ درجه دوران دهیم و نتیجه دوران، روی خودش منطبق شود، میگوییم شکل مرکز تقارن دارد و نقطه مورد نظر، مرکز تقارن شکل است. مثلاً اگر شکل مشکی رنگ زیر را حول نقطهٔ \( \Large O \) به اندازه 180 درجه دوران دهیم، بر روی خودش قرار میگیرد، پس این نقطه، مرکز تقارن شکل خواهد بود.
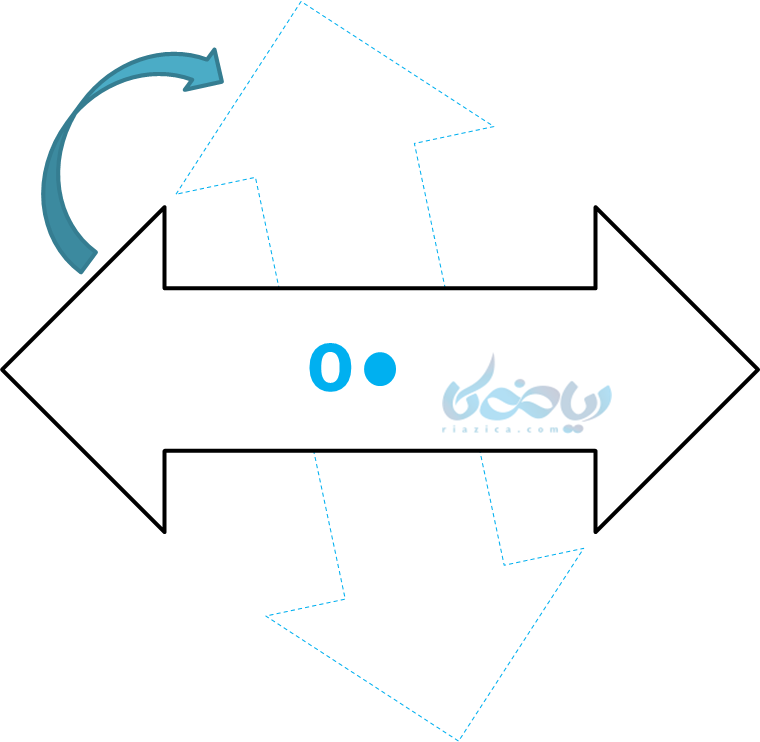
راه تشخیص مرکز تقارن
برای این که بدانیم شکلی مرکز تقارن دارد یا خیر، در وسط آن شکل نقطهای در نظر میگیریم. اگر از هر نقطه روی شکل به نقطه وسط، خطی رسم کرده و به همان اندازه ادامه دهیم و انتهای خط روی شکل قرار بگیرد، آن نقطه، مرکز تقارن شکل خواهد بود.
مثال 4: آیا شکلهای زیر مرکز تقارن دارند؟

حل 4:
الف) نقطه مرکز دایره را در نظر میگیریم، نقاطی مانند \( \Large A \) و \( \Large B \) روی شکل انتخاب کرده و به نقطه \( \Large O \) وصل میکنیم، به همان اندازه ادامه میدهیم . چون نقاط انتهایی (یعنی \( \Large A’ \) و \( \Large B’ \)) روی شکل قرار دارند، پس \( \Large O \) مرکز تقارن شکل خواهد بود.
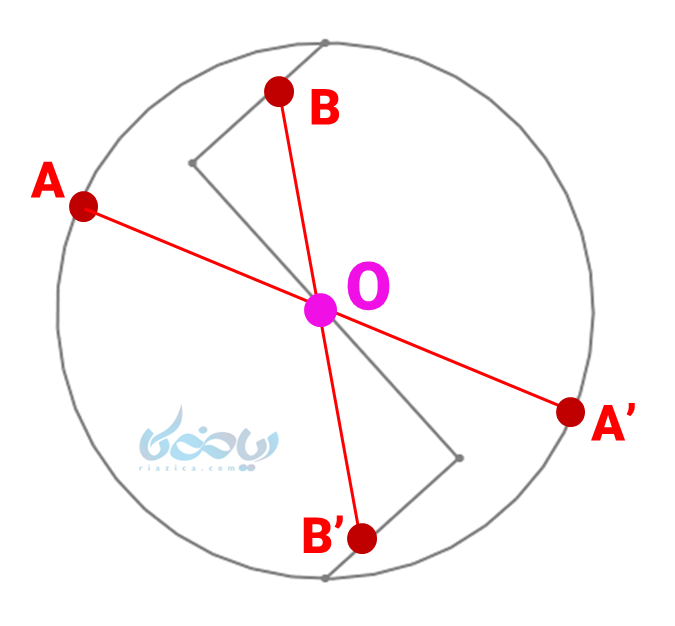
ب) نقطهای در وسط مثلث مانند \( \Large O \) در نظر میگیریم، اگر از نقطه \( \Large A \) به نقطه \( \Large O \) وصل کرده و به همان اندازه ادامه دهیم، نقطه انتهایی (یعنی \( \Large A’ \)) روی شکل قرار نمیگیرد، پس مثلث مرکز تقارن ندارد.
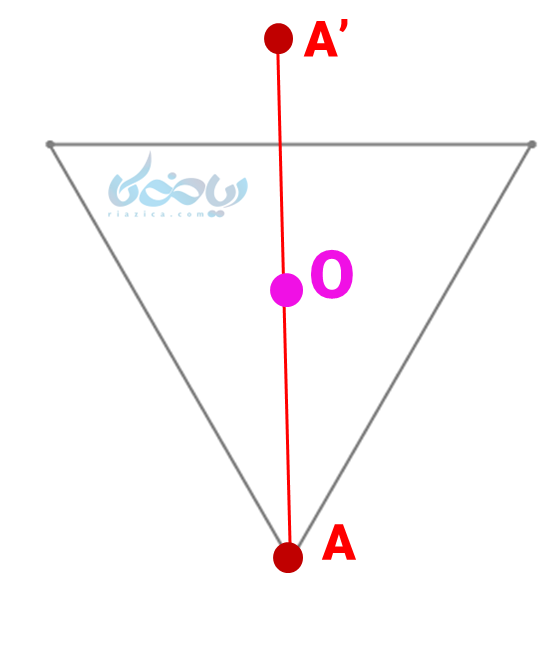
ساختن شکل دارای مرکز تقارن
مثال 5: شکل زیر را به گونهای کامل کنید که نقطۀ \( \Large O \) مرکز تقارن آن باشد.
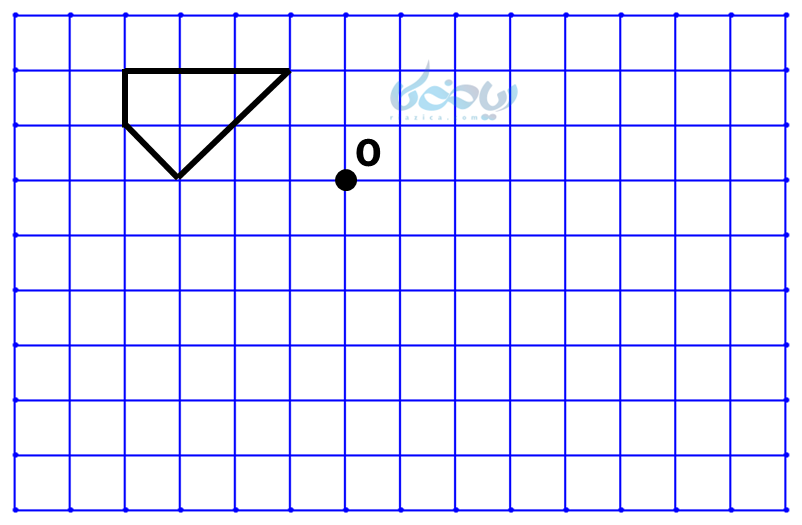
حل 5:
مطابق روشی که برای تشخیص مرکز تقارن بیان کردیم، در صورتی نقطۀ \( \Large O \) مرکز تقارن شکل است که با وصل کردن هر نقطه به آن و ادامه دادن به همان اندازه باز هم به روی شکل برسیم.
پس باید چهار رأس این چهارضلعی را به نقطۀ \( \Large O \) وصل کرده و به همان اندازه امتداد دهیم تا چهار نقطه جدید ایجاد شود. از صفحه شطرنجی میتوانیم استفاده کنیم، مثلاً فاصله نقطه بالا سمت راست تا نقطۀ \( \Large O \)، یک واحد به راست و دو واحد پایین است. پس از نقطه \( \Large O \) هم به همین ترتیب آن را ادامه دادهایم:
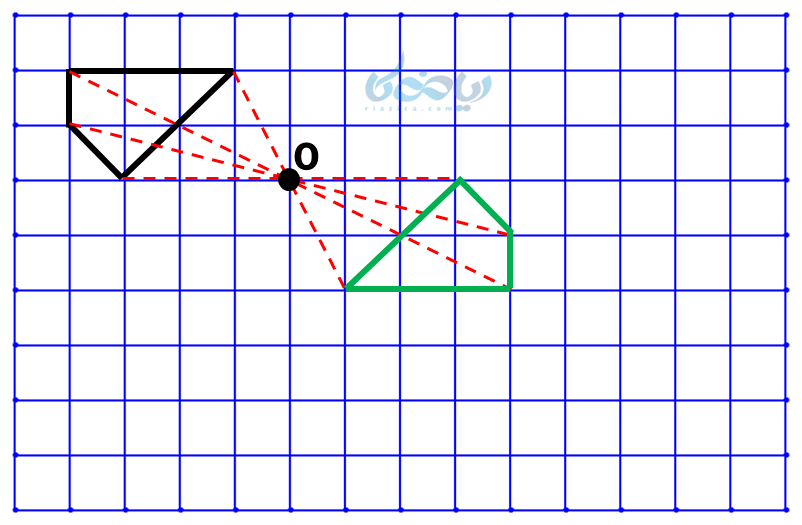
با وصل کردن این نقاط به هم، چهار ضلعی سبز رنگ رسم میشود. حالا نقطۀ \( \Large O \) مرکز تقارن (شکل مشکی + شکل سبز) است.
مرکز تقارن در چندضلعی منتظم
اینجا این سوال پیش می آید کدامیک از چند ضلعیهای منتظم مرکز تقارن درند؟
چند ضلعیهای منتظم، اگر تعداد اضلاع زوج باشد، مرکز تقارن دارند و اگر تعداد اضلاع فرد باشد، مرکز تقارن ندارند. به عنوان مثال 8 ضلعی منتظم مرکز تقارن دارد، اما 5 ضلعی منتظم مرکز تقارن ندارد.
مثال 6: کدامیک از شکلهای هندسی زیر هم خط تقارن و هم مرکز تقارن دارد؟
الف) مثلث متساویالاضلاع ب) هفتضلعی منتظم ج) مربع د) نهضلعی منتظم
حل 6:
مثلث متساوی الاضلاع، سه ضلعی منتظم و مربع، چهار ضلعی منتظم هستند. در بخشهای قبل دیدیم که چند ضلعیهای منتظم به تعداد اضلاعشان خط تقارن دارند، پس همه این شکلها دارای خط تقارن هستند.
گزینههای (الف) تا (د) به ترتیب 3، 7، 4 و 9 ضلع دارند و از آنجا که چند ضلعیهای منتظم با تعداد اضلاع زوج دارای مرکز تقارن هستند، پس فقط 4ضلعی منتظم (مربع) دارای مرکز تقارن است.
چند نکته در مورد خط تقارن اشکال هندسی
متوازی الاضلاع شکلی که مرکز تقارن دارد ولی خط تقارن ندارد
یکی از شکلهای جالب توجه در این درس، متوازی الاضلاع است. متوازی الاضلاع چند خط تقارن دارد؟ بیایید با هم ببینیم. چهار خط تقارن احتمالی را برای این شکل رسم کردهایم: دو قطر متوازی الاضلاع و دو خط عمودی و افقی که از مرکز میگذرد. از روش تشخیص خط تقارن ریاضی هشتم در این شکل دیده میشود که هیچ یک از این خطوط، خط تقارن نیست.
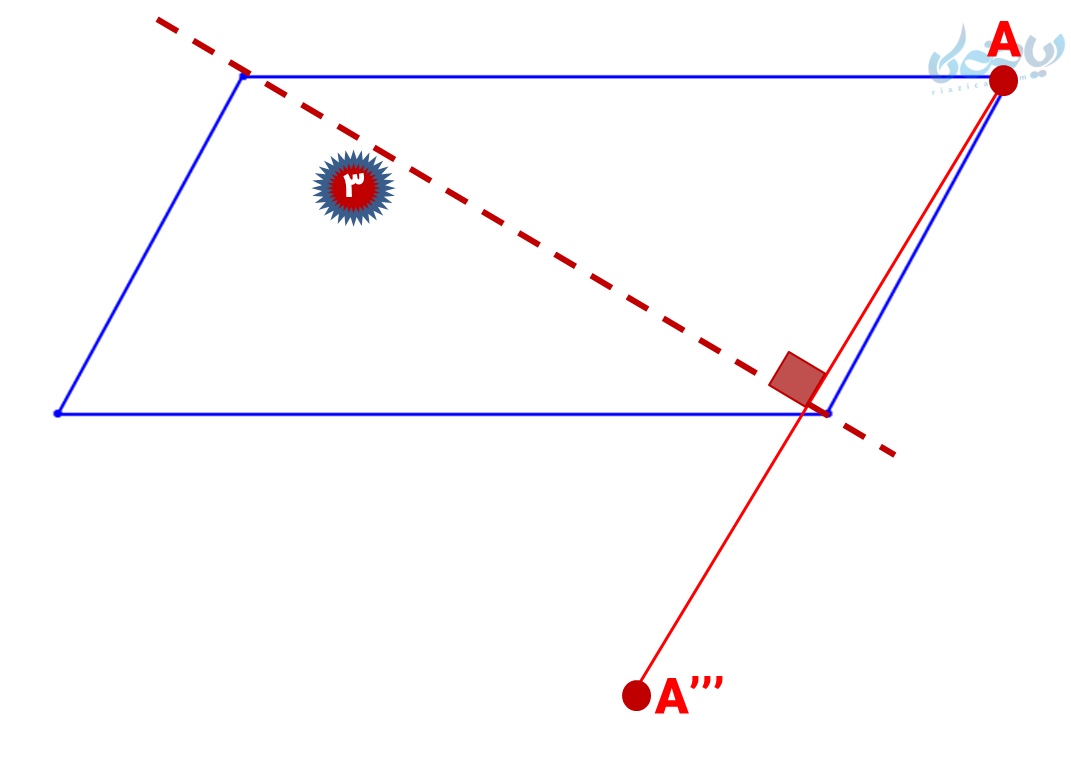
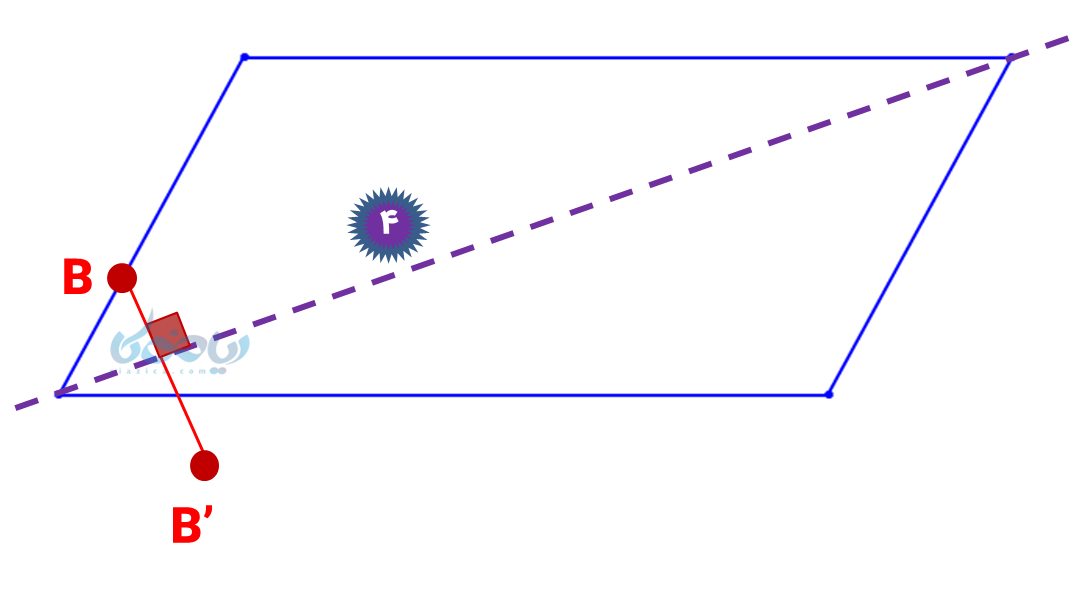
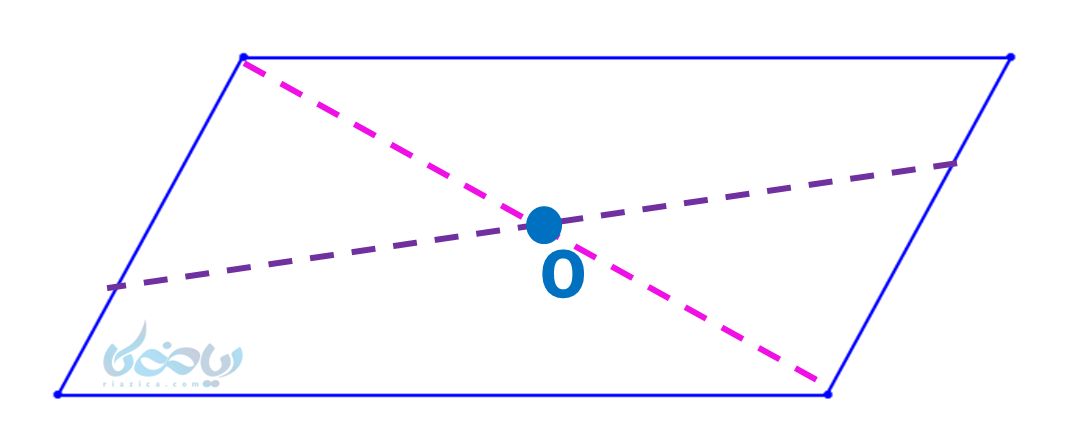
متوازی الاضلاع مرکز تقارن دارد، به شکل زیر توجه کنید؛ هر نقطهای روی شکل را به مرکز وصل کرده و به همان اندازه ادامه دهیم روی شکل قرار میگیرد.
شکلی که بیش از دو خط تقارن دارد ولی مرکز تقارن ندارد
قبلاً گفتیم که همه چند ضلعیهای منتظم خط تقارن دارند، اما تنها چند ضلعیهای منتظمی مرکز تقارن دارند که تعداد اضلاع آنها زوج باشد. بنابراین چند ضلعیهای منتظم با تعداد اضلاع فرد دارای بیش از دو محور تقارن، اما فاقد مرکز تقارن هستند.
در ادامه درسنامه خطوط موازی ومورب روحتما مطالعه کنید.
زنگ آخر کلاس خط تقارن ریاضی هشتم
اولاً امیدوارم از مطالعه این درس لذت برده باشید! قطعاً بعد از خواندن این درس به جای تا زدن شکل هندسی چشم بسته میتونی بگی متقارن هست یا نه؟ در این محتوا با چندضلعی و نوع خاصی از آن به نام چندضلعی منتظم آشنا شدیم. با روشهای ساده توانستیم خط تقارن و مرکز تقارن شکلهای هندسی را پیدا کنیم.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاهها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی هشتم به شما پیشنهاد میدهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!





سلام وخسته نباشید من میخواستم بدونم ۱۲ضلعی منتظم خط تقارن داره یا نداره
با عرض سلام و خسته نباشید.
چند ضلعی منتظم به تعداد اضلاعش، خط تقارن دارد. یعنی ۱۲ ضلعی منتظم، ۱۲ خط تقارن دارد.
سلام بله دارد . هر n ضلعی منتظم ، به تعداد ضلع هایش خط تقارن ( محور تقارن ) دارد . پس ۱۲ ضلعی منتظم ، ۱۲ تا محور تقارن دارد
سلام
ممنون از پاسخگویی شما
سلام و خسته نباشید
خیلی مطالب خوبی داشت ممنون از شما لطفاً بیشتر بزارید
سلام ممنون از انرژیتون حتما ادامه میدیم.
سلام ممنون نکات بسیار مفید و عالیای گفته بودید با تشکر
سلام ممنون از انرژی پر مهرتون.
سلام عالی بود
سلام و عرض ادب
متشکرم از توجهی که داشتید.
موفق باشبد.
خوب بود
تشکر از انرژی مثبت شما
چند ضلعی هایی که اضلاع ان ها فرد است چه چیز تقارن ندارد؟؟؟
سلام دوست عزیز
بستگی به شکل ومحدب بودن ومقعر بودن شکل داره ونمیشه حکم کلی داد
فقظ چند ضلعی های منتظم که تعداد اضلاع فرد است مرکز تقارن ندارند وبه تعداد اضلاع محور تقارن دارند
چند ضلعی های منتطم با تعداد اضلاع فرد مرکز تقارن ندارند
سلام و خسته نباشید اندازه مجهول هارو اگر که میشه توضیح دهید
سلام دوست عزیز منظورتون در معادله هست؟
عالی بود مشکلم رفع شد
خیلی ممنون خداخیرتون بده
سلام و عرض ادب
ممنون از انرژی که دادید.
موفق باشید.
۱۰ضلعی منتظم و ۱۷ ضلعی منتظم چند خط تقارن و چند محور تقارن دارد
سلام دوست عزیز
چند ضلعیهای منتطم به اندازه اضلاعشان محور تقارن دارن خظ تقارن ومحور تقارن هر دو یک مفهوم دارند در مورد مرکز تقارن هم ده ضلعی مرکز تقارن دارد ۱۷ ضلعی ندارد
سلام
معلم ما بهمون سوال داده گفته 1 محور تقارن توی متواضی الاضلاع پیدا کنید. جوابش چی میشه؟
سلام و عرض ادب
متوازی الاضلاع محور تقارن ندارد ولی مرکز تقارن دارد. اما مربع و لوزی که نوعی متوازی الاضلاع محور تقارن دارند.
موفق باشید.
سلام. سخاوتمندانه نکته های زیادی گفتید .خدا خیرتون بده.
با سلام وعرض ادب خرسندیم که براتون مفید بوده
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
???خوبه
با سلام وعرض ادب
ممنون از انرژی شما
سلام و خسته نباشید ۲۰ ضلعی منتظم دارای چند محور تقارن دارد ؟؟؟
با سلام وعرض ادب
همونطور که در پست گفتیم چند ضلعی منتظم به تعداد اضلاعش، خط تقارن دارد پس ۲۰ تا دارد
۲۰ ضلعی منتظم دارای چند محور تقارن دارد؟؟
خیلی عالی بود
با سلام واحترام
ممنون از نظر لطف شما
با سلام دو خط متقاطع چند محور تقارن و چند مرکز تقارن دارد
با سلام
دو خطمتقاطع مرکز و محور تقارن ندارن
سلام ۸ ضلعی مرکز تقارون و محور تقارون و مجموع زاویه داره یا ن و تعدادش؟! 🙂 ممنون
با سلام وادب
اگه پست رو خوب مطالعه میکردید متوجه میشدید چندضلعی های منتظم به اندازه اضلاعشان محور تقارن دارن وآنهایی که تعداد اضلاعشان زوج است مرکز تقارن دارند
سلام برای تفهیم خط تقارن به دانش آموزان پایه سوم از برش میوه استفاده کردم که آن ها خط تقارن را با قطر یکی ندانندو آن را خط فرضی بدانند که همانند چاقویی هست که جهت تقسیم مساوی شکل استفاده می شود.
با توجه به توضیحات شما راه تشخیص خط تقارن باید روی سطح شکل را قرار بگیرد پس نمی توان گفت خطی برای تقسیم مساوی شکل.
راهنمایی بفرمایید
با سلام وادب
متاسفانه مثال خوبی رو انتخاب نکردید چون سیب یک جسم سه بعدی است اما ما خطتقارن رو برای شکلهای دو بعدی تعریف میکنیم بهترین راه برای بچه های ابتدایی برش اشکال هندسی روی مقوا وتا زدن آنهاست
باسلام و خسته نباشید به شما
خیلی ممنون…عالی بود
باسلام و خسته نباشید به شما
متشکرم…عالی بود
با سلام وادب
خوشحالیم مفید بوده
عالی بود مرسی..
با سلام
ممنون از انرژی که به ما میدید برای ادامه مسیر
واقعا عالی من که همه چی رو فهمیدم مرسی
با سلام وادب
خدا رو شکر دوست عزیز
سلام چند ضلعی منتظم با ضلع های فرد با چه قانونی میتوان تعدادشان را یافت یک گل ۵برگ محور تقارن دارد چندتا
با سلام دوست عزیز
تعداد چه چیزی رو یافت ؟