آموزش ریاضی پایه هشتم
خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
قاعدهای طلایی در مورد اعداد رادیکالی! ضرب و تقسیم اعداد رادیکالی چگونه انجام میشود؟ کافی است همین چند نکته کوچک این درسنامه از مجموعه آموزش ریاضی پایه هشتم را دنبال کنید. در این مطلب خواص ضرب و تقسیم رادیکال ها ریاضی هشتم را خواهید آموخت و از این نکات برای همیشه استفاده خواهید کرد. این درس آسون میشه اگه تا آخر مطلب رو با ما باشی…
خواص ضرب و تقسیم رادیکال ها ریاضی هشتم
ممکن است چند عدد زیر رادیکال با هم جمع و تفریق یا ضرب و تقسیم شده باشند. برای انجام اعمال جبری روی اعداد رادیکالی (یعنی ضرب و تقسیم رادیکال ها و همچنین جمع وتفریق آنها) به نکات زیر توجه کنید:
ضرب و تقسیم اعداد رادیکالی
علامت ضرب و تقسیم را میتوان از رادیکال بیرون آورد. به عبارتی خواص ضرب و تقسیم رادیکال ها ریاضی هشتم را میتوان چنین خلاصه نمود:
\( \LARGE \sqrt {a × b} = \sqrt {a} × \sqrt {b} \)
\( \LARGE \sqrt {\frac {a}{b}} = \frac {\sqrt {a}}{\sqrt {b}} \)
در این مورد به نمونه زیر توجه کنید:
حاصل عبارت \( \Large \sqrt {16} × \sqrt {25} \) را محاسبه میکنیم:
\( \Large \sqrt{16} = 4 \text{ , } \sqrt{25} = 5 \)
\( \Large \sqrt {16} × \sqrt {25} = 5 × 4 = 20 \)
حالا عبارت \( \Large \sqrt {16 × 25} \) را محاسبه میکنیم:
\( \Large \sqrt {16 × 25} = \sqrt {400} = 20 \)
در این نمونه مشاهده کردیم که علامت ضرب را میتوان از زیر رادیکال بیرون آورد (برای تقسیم هم همین اصل برقرار است).
جمع و تفریق اعداد رادیکالی
علامت جمع و تفریق را «نمیتوان» از رادیکال بیرون آورد. به بیان ریاضی:
\( \Large \sqrt {a \pm b} \ne \sqrt {a} \pm \sqrt {b} \)
به عنوان نمونه ببینید آیا جذر مجموع 36 و 64 با مجموع جذرهای آنها برابر شده است؟
\( \Large \sqrt{36} = 6 \text{ , } \sqrt{64} = 8 \)
\( \Large → \sqrt{36} + \sqrt{64} = 14 \)
\( \Large \sqrt{36 + 64} = \sqrt{100} = 10 \)
\( \Large 14 \ne 10 \).
مثال1: حاصل \( \Large \sqrt {\frac {16}{9}} \) و \( \Large \sqrt {4 × 10} \)را بدست آورید.
حل 1:
با توجه به خواص ضرب و تقسیم رادیکال ها ریاضی هشتم میتوانیم علامتهای ضرب و تقسیم را به راحتی از زیر رادیکال خارج کنیم، پس خواهیم داشت:
\( \Large \sqrt {\frac {16}{9}} = \frac {\sqrt {16}}{\sqrt {9}} \)
\( \Large = \frac {4}{3} \)
\( \Large \sqrt {4 × 10} = \sqrt {4} × \sqrt {10} \)
\( \Large = 2 \sqrt {10} \)
نکته: اگر عددی حاصلضرب دو عدد باشد و بخواهیم از آن جذر بگیریم، در صورتی که یکی از آن دو عدد جذر صحیح داشته باشند، میتوانیم جذر صحیح را از زیر رادیکال خارج کنیم.
به عنوان مثال \( \Large \sqrt {50} \) را میتوان بصورت حاصلضرب 25 در 2 نوشته و طبق خواص ضرب و تقسیم رادیکال ها ریاضی هشتم به شکل زیر بنویسیم:
\( \Large \sqrt {25 × 2} = \sqrt {25} × \sqrt {2} \)
\( \Large = 5 \sqrt {2} \)
مثالی ترکیبی خواص ضرب و تقسیم رادیکال ها ریاضی هشتم با مبحث «جذر تقریبی»
مثال 2: حاصل \( \Large \sqrt {800} \) را بصورت تقریبی تا یک رقم اعشار بدست آورید.
حل 2:
عدد 800 حاصلضرب اعداد 8 و 100 است؛ پس میتوانیم با توجه به خواص ضرب و تقسیم رادیکال ها ریاضی هشتم آن را بصورت زیر ساده کنیم:
\( \Large \sqrt {8 × 100} = \sqrt {8} × \sqrt {100} \)
\( \Large = 10 \sqrt {8} \)
حال برای محاسبه این جذر، مطابق روش درسنامه جذر تقریبی مقدار \( \Large \sqrt {8} \) را محاسبه کرده و در 10 ضرب میکنیم.
- تا چند رقم اعشار؟در صورت سؤال گفته شده «تا یک رقم اعشار». آیا باید \( \Large \sqrt {8} \) را تا یک رقم اعشار محاسبه کنیم؟
- خیر! چون \( \Large \sqrt {8} \) در 10 ضرب میشود، یک رقم اعشار کم میشود، پس باید \( \Large \sqrt {8} \) را تا 2 رقم اعشار محاسبه کنیم تا حاصلضرب آن در 10 دارای یک رقم اعشار باشد:
\(\Large 4 < 8 < 9 \)
\(\Large → \sqrt {4} < \sqrt {8} < \sqrt {9} \)
\(\Large → 2 < \sqrt {8} < 3 \)
مقدار میانی این دو عدد (یعنی 2/5) را امتحان میکنیم: مقدار \(\Large (2/5)^2 \) برابر با 6/25 است. پس اعداد بزرگتر از آن را بررسی میکنیم.
| 2/9 | 2/8 | 2/7 | 2/6 | عدد |
|---|---|---|---|---|
| 8/41 | 7/84 | 7/29 | 6/76 | مجذور |
مطابق جدول، عدد 8 بین مجذور اعداد 2/8 و 2/9 قرار دارد (\(\Large 2/8 < \sqrt {8} < 2/9 \))؛ سپس عدد میانی (یعنی 2/85) را بررسی میکنیم: مقدار \(\Large (2/85)^2 \) برابر با 8/12 است. پس اعداد کوچکتر از آن را بررسی میکنیم.
| 2/84 | 2/83 | 2/82 | 2/81 | عدد |
|---|---|---|---|---|
| 8/07 | 8/01 | 7/95 | 7/90 | مجذور |
بنابراین مقدار تقریبی \( \Large \sqrt {8} \) تا 2 رقم اعشار برابر است با: 2/83 .
\( \Large 10 \sqrt {8} = 10 × 2/83 \simeq 28/3 \)
نکته: دقت کنید که این روش را فقط زمانی استفاده کنید که عدد زیر رادیکال مضربی از 100 باشد؛ چون در مورد اعداد دیگر، دقت اعشاری کم خواهد شد.
مثال 3: عبارت \( \Large 3 \sqrt{3} \) برابر با کدام گزینه است؟
الف) \( \Large \sqrt {6} \) ب) \( \Large \sqrt {33} \) ج) \( \Large \sqrt{27} \) د) \( \Large \sqrt{9} \)
حل 3:
این عبارت، حاصلضرب یک عدد صحیح در یک عدد رادیکالی است، برای آن که حاصل بصورت یک عدد زیر رادیکال باشد باید از خواص ضرب و تقسیم رادیکال ها ریاضی هشتم استفاده کنیم. 3 را بصورت \( \Large \sqrt{9} \) مینویسیم:
\( \LARGE \sqrt{9} × \sqrt {3} =\sqrt{9 × 3} \)
\( \LARGE =\sqrt {27} \)
یک مثال هوشمندانه
مثال 4: حاصل عبارت \( \Large 4 – \sqrt{6/25} \) را محاسبه نمایید.
حل 4:
نظرتون چیه \( \Large \sqrt{6/25} \) که یه عدد اعشاری هست از روش جذر تقریبی بدست بیاریم؟
- اووووه! لقمه رو دور سرت نپیچون!!! راه سادهتری هم هست. یه کم دقت کن!
بهتر است از خواص ضرب و تقسیم رادیکال ها استفاده کنیم. 6/25 را بصورت \( \Large \frac {25}{4} \) مینویسیم؛ پس خواهیم داشت:
\( \LARGE \sqrt {\frac {25}{4}} = \frac {\sqrt {25}}{\sqrt {4}} \)
\( \LARGE = \frac {5}{2} = 2/5 \)
بنابراین حاصل عبارت \( \Large 4 – \sqrt{6/25} \) برابر است با:
\( \LARGE = 4 – 2/5 = 1/5 \)
شاید بعضی بگن ما نمیدونستیم 6/25 را بصورت \( \Large \frac {25}{4} \) میشه نوشت اشکال نداره کافیه این عدد رو به شکل کسر \( \Large \frac {625}{100} \) بنویسید وبه همین روش به همین جواب برسید.
مثال 5: با ذکر دلیل مشخص کنید که نقاط A و B روی محور زیر نشاندهنده کدام یک از اعداد زیر میباشد؟
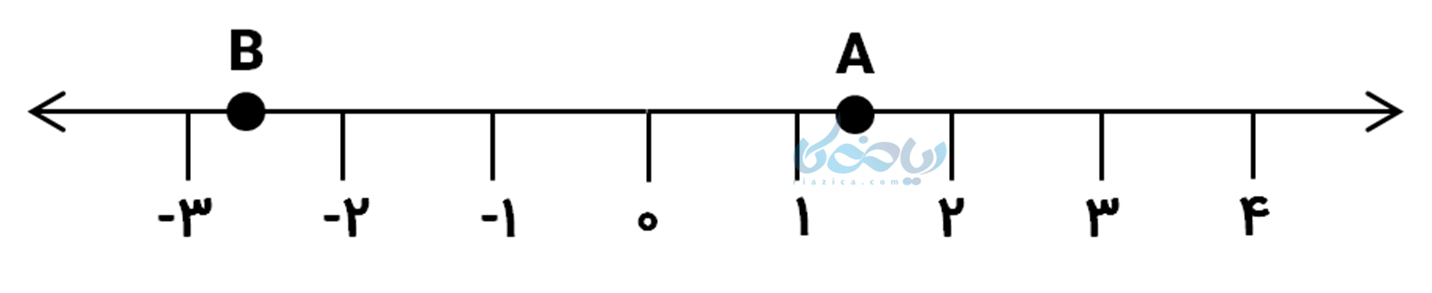
\( \Large – \sqrt{8} \text { , } -\sqrt{6/25} \)
\( \Large \sqrt{1/25} \text { , } \sqrt{2/25} \)
حل 5:
برای حل این سؤال، اولین کاری که میکنیم این است که محل تقریبی اعداد داده شده را روی محور مشخص میکنیم:
میدانیم که اعداد \( \Large – \sqrt{8} \) و \( \Large – \sqrt{6/25} \) هر دو بین (3-) و (2-) قرار دارند؛ چون:
\( \Large 4 < 6/25 < 9 \)
\(\Large → \sqrt {4} < \sqrt {6/25} < \sqrt {9} \)
\(\Large → 2 < \sqrt {6/25} < 3 \)
توجه کنید که این روشی است که در درسنامه جذر تقریبی هم از آن استفاده میکردیم. حال طرفین را در یک علامت منفی ضرب میکنیم:
\(\Large → -3 < – \sqrt {6/25} < -2 \)
برای عدد \( \Large – \sqrt{8} \) هم همین کار را انجام میدهیم:
\( \Large 4 < 8 < 9 \)
\(\Large → \sqrt {4} < \sqrt {8} < \sqrt {9} \)
\(\Large → 2 < \sqrt {8} < 3 \)
\(\Large → -3 < – \sqrt {8} < -2 \)
حالا نوبت محل تقریبی اعداد \( \Large \sqrt{1/25} \) و \( \Large \sqrt{2/25} \) است که هر دو بین (1) و (2) قرار دارند؛ چون:
\( \Large 1 < 1/25 < 4 \)
\(\Large → \sqrt {1} < \sqrt {1/25} < \sqrt {4} \)
\(\Large → 1 < \sqrt {1/25} < 2 \)
\( \Large 1 < 2/25 < 4 \)
\(\Large → \sqrt {1} < \sqrt {2/25} < \sqrt {4} \)
\(\Large → 1 < \sqrt {2/25} < 2 \)
توجه کنید که الان در فاصله (3-) تا (2-) دو عدد و در فاصله (1) تا (2) دو عدد داریم؛ پس باید محل دقیقتری از آنها پیدا کنیم.
کمی دقیقتر!
برای مشخص کردن جای دقیقتر اعداد روی محور میتوانیم از خواص ضرب و تقسیم رادیکال ها ریاضی هشتم استفاده کنیم:
\( \Large 2/25 = \frac {9}{4} \)
\( \Large → \sqrt {2/25} = \sqrt{\frac {9}{4}} \)
\( \Large = \sqrt{\frac {9}{4} }= \frac {\sqrt{9}}{\sqrt{4}} \)
\( \Large = \frac {3}{2} = 1/5 \)
\( \Large 6/25 = \frac {25}{4} \)
\( \Large → \sqrt {6/25} = \sqrt{\frac {25}{4}} \)
\( \Large = \sqrt{\frac {25}{4} }= \frac {\sqrt{25}}{\sqrt{4}} \)
\( \Large = \frac {5}{2} = 2/5 \)
مشاهده میشود که \( \Large \sqrt{2/25} \) برابر با 1/5 شده است، اما نقطه A روی محور از 1/5 کمتر است. از سویی میدانیم:
\( \Large 1/25 < 2/25 \)
\( \Large → \sqrt{1/25} < \sqrt{2/25} \)
پس نقطه A نشاندهنده \( \Large \sqrt{1/25} \) است.
همچنین \( \Large -\sqrt{6/25} \) برابر با 2/5- است، در حالی که نقطه B روی محور از 2/5- کمتر است. از طرفی:
\( \Large 6/25 < 8 → \sqrt{6/25} < \sqrt{8} \)
\( \Large → -\sqrt{8} < -\sqrt{6/25} \)
بنابراین نقطه B نشاندهنده \( \Large -\sqrt{8} \) است.
قسمتی از ویدیو خواص ضرب و تقسیم رادیکال ها ریاضی هشتم
برای خرید کامل این ویدیو دکمه زیر این ویدیو را بزنید:
زنگ آخر کلاس خواص ضرب و تقسیم رادیکال ها ریاضی هشتم
در این محتوا با نکته مهمی از عددهای رادیکالی یعنی خواص ضرب و تقسیم رادیکال ها ریاضی هشتم آشنا شدیم و در کنار آن دقت کردیم که علامتهای جمع و تفریق از زیر رادیکال خارج نمیشود. در ادامه با حل چندین مثال متنوع توانستیم به این مبحث مسلط شویم.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاهها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی هشتم به شما پیشنهاد میدهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!





چجوری میتونیم بفهمیم بین یه عددی چه عددی قرارداره؟
سلام ووقت به خیر
مظورتون بین دو عدد کویا یا همون کسری هست؟
چند عدد بین رادیکال ۳ و رادیکال ۱۰ هست ؟لطفا با توضیح بگین
سلام و عرض ادب
اگر منظورتون عدد حقیقی هست بی نهایت عدد وجود دارد اما اگر منظورتون عدد صحیح است ۲ و ۳ وجود دارد. چون جذر رادیکال ۳، ۱.۷ و جذر رادیکال ۱۰، ۳.۱ می باشد.
برای ساده کردن عبارت های رادیکالی که در اون جمع ، تقسیم و ضرب به کار رفته باید چگونه عمل کنیم
با سلام وعرض احترام
این پست وپستی که در زیر لینکش رو قرار میدم استفاده کنید به جواب میرسید
https://riazica.com/finding-roots-and-radicals/
سلام استاد
میشه جواب رادیکال 2 در رادیکال 15 بدید…
و توضیخات و راهنمایی ام کنید…
ممنون
با سلام واحترام
چون بین دو رادیکال ضرب هست وفرجه ها یکی هستن اعداد زیر رادیکال در هم ضرب میشن ومیشه رادیکال ۳۰
نایس.
برا شب امتحان عالیه.
با سلام دوست عزیز
خدا رو شکر مفید بوده
سلام میشه راهنمایی کنید چجوری ۱۲√ تقسیم بر ۲ میشه رادیکال ۳؟
سلام دوست عزیز
چون دوازده میشه سه ضربدر چهار وجذر چهار میشه ۲ واز زیر رادیکال میاد بیرون وبا ۲ مخرج ساده میشه ومیمونه فقط رادیکال ۳
نایس
ممنون دوست عزیز
سلام رادیکال ۴ تقسیم بر ۴؟
با سلام
میشود یک دوم
ضرب ۷√ و ۸√ چی میشه
رادیکال ۵۶ که ساده میشه به دو رادیکال ۱۴
سلام ببخشید ایا میشه یه عدد طبیعی رو در یک رادیکال یا ضریب او ضرب کنیم؟
سلام ببخشید ایا میشه یه عدد طبیعی رو در یک رادیکال یا ضریب او ضرب کنیم؟
همچنین میشه جمع یا تفریق کرد
با سلام وادب
یه عدد رو در ضریب رادیکال میشه ضرب وتقسیم کرد ولی جمع وتفریق نمیشه