آموزش ریاضی پایه هشتم
نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
تو میگی میتونم یک عدد رادیکالی رو بصورت حدودی روی محور اعداد نشون بدم. ولی اگه بخوام دقیق دقیق نشون بدم چی؟؟ من جوابم اینه که خیالت راحت. قبلاً اصولش رو یاد گرفتی، توی همین ریاضی هشتم! این درسنامه از سری آموزش ریاضی پایه هشتم روش نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم را بصورت کامل آموزش میدهد. خواهیم دید که این کار به سادگی با استفاده از رابطه فیثاغورس انجام میشود.
نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم
در درسنامه جذر تقریبی، یاد گرفتیم که چگونه میتوان یک عدد رادیکالی را بصورت تقریبی بر روی محور اعداد نشان داد. اما با استفاده از رابطه فیثاغورس در مثلثهای قائمالزاویه (ریاضیات پایه هشتم، فصل ششم، درس اول) میتوانیم بصورت دقیق آن را نشان دهیم.
رسم یک خط با طولی به اندازه یک عدد رادیکالی
فرض کنید میخواهیم خطی به طول \(\Large \sqrt {a} \) رسم کنیم. برای این کار کافی است دو عدد پیدا کنیم که جمع مجذور این دو برابر با \(\Large (\sqrt {a})^2 \) یا همان \(\Large {a} \) شود. یعنی:
\(\Large x^2+y^2= (\sqrt {a})^2 \)
\(\Large x^2+y^2= a \)
این رابطه، رابطه فیثاغورس است. پس اگر مثلث قائمالزاویهای با دو ضلع \(\Large x \) و \(\Large y \) رسم کنیم، وتر آنها برابر با \(\Large \sqrt {a} \) خواهد شد.
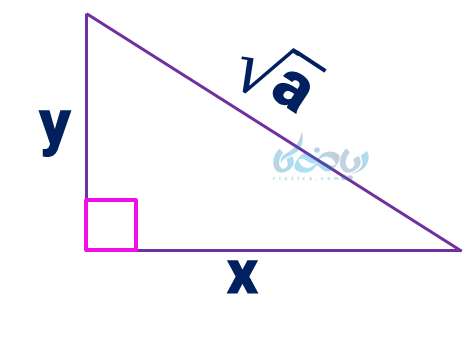
به عنوان نمونه مثلثهای شکل زیر را در نظر بگیرید. در این شکل نحوه رسم 4 خط با طولهای رادیکالی مختلف نشان داده شده است:
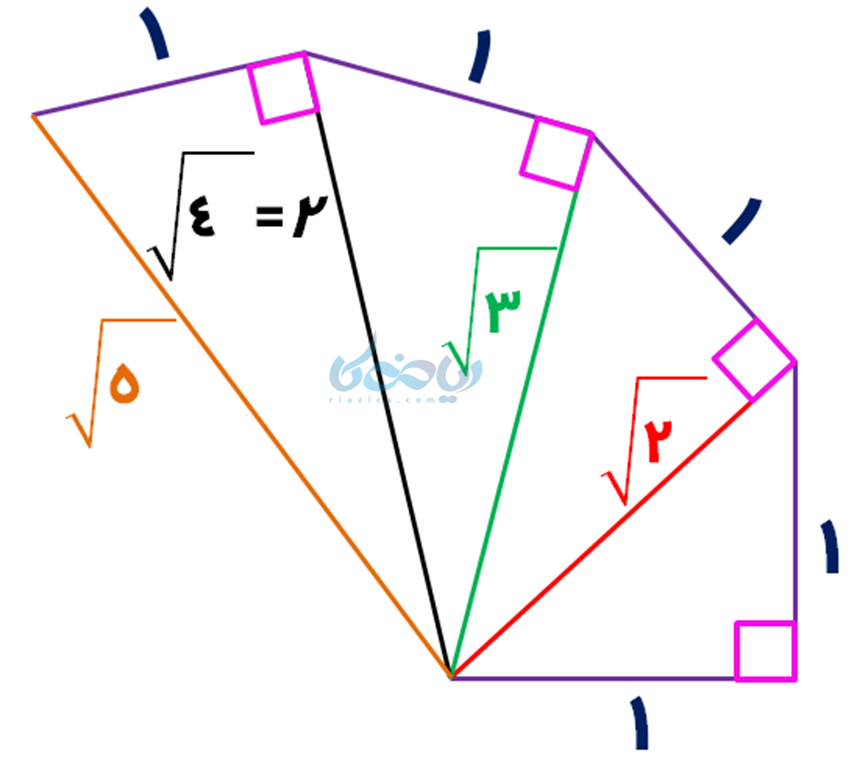
در این شکل، ابتدا در مثلث پایین سمت راست مثلث قائمالزاویهای با اضلاع 1 و 1 رسم شده است. مطابق رابطه فیثاغورس میدانیم که وتر آن (\( \Large c \)) برابر با \(\Large \sqrt {2} \) است. چون:
\(\Large 1^2+1^2= c^2 \)
\(\Large c^2 = 2 \)
\(\Large c = \sqrt {2} \)
طول وترهای بعدی هم با همین روش از رابطه فیثاغورس بدست میآید. بدین ترتیب میتوان با رسم یک یا چند مثلث قائمالزاویه، اندازه اعداد رادیکالی را روی کاغذ نشان داد.
با این مقدمه و حل یک مثال خوب میتوانیم سراغ نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم برویم.
یک مثال ساده از نمایش اعداد رادیکالی روی محور اعداد
مثال 1: خطی به طول \(\Large \sqrt {6} \) رسم کنید.
حل 1:
برای این کار باید مثلث قائمالزاویهای با دو ضلع \(\Large x \) و \(\Large y \) رسم کنیم که وتر آنها برابر با \(\Large \sqrt {6} \) باشد. مطابق رابطه فیثاغورس دو عدد پیدا میکنیم که جمع مجذور این دو برابر با 6 شود. یعنی:
\(\Large x^2+y^2=6 \)
میتوانیم \(\Large \sqrt {5} \) و \(\Large 1 \)را در نظر بگیریم. چون:
\(\Large (\sqrt {5})^2+1^2= 5+1=6 \)
بنابراین باید مثلث قائمالزاویهای به اضلاع \(\Large \sqrt {5} \) و \(\Large 1 \) رسم کنیم. طول وتر برابر با 6 خواهد بود. اما توجه کنیم که ابتدا باید برای \(\Large \sqrt {5} \) همین کار را انجام دهیم:
جمع مجذورهای اعداد 1 و 2 برابر با 5 است. پس با رسم مثلث قائمالزاویهای با اضلاع 1 و2 وتر برابر با (\(\Large \sqrt {5} \)) خواهد بود.
\(\Large 1^2+2^2= 1+4=5 \)
بنابراین با رسم دو مثلث قائمالزاویه، یکی با اضلاع 1 و 2 (برای بدست آوردن وتر \(\Large \sqrt {5} \) ) و دیگری با اضلاع 1 و \(\Large \sqrt {5} \) به وتری با طول \(\Large \sqrt {6} \) خواهیم رسید:
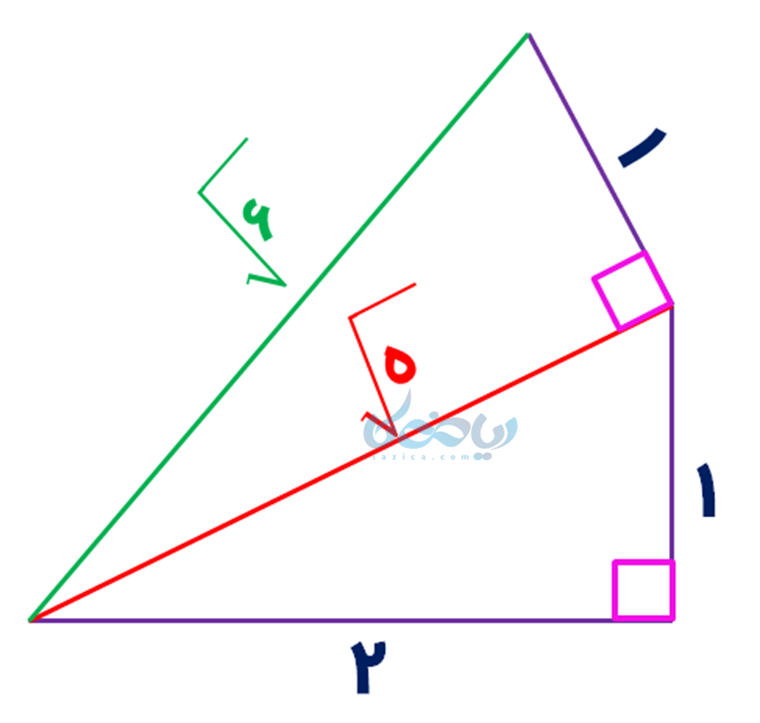
مراحل نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم
برای نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم با توجه به مراحل زیر عمل میکنیم: (بیایید با هم روش نمایش عدد \( \Large 1- \sqrt{2} \) را ببینیم)
- مشخص کردن مبدأ حرکت: از عدد صحیح یا کسری که با عدد رادیکالی جمع شده است شروع میکنیم. (اگر فقط عدد رادیکالی باشد، مبدأ ما عدد صفر است) «در این مثال، مبدأ حرکت، عدد 1 خواهد بود».
- تعیین دو عدد که جمع مجذور آنها برابر با عدد زیر رادیکال باشد (اضلاع مثلث قائمالزاویه): (مطابق روش رسم یک خط با طولی به اندازه یک عدد رادیکالی که در بالا توضیح داده شد) «در این مثال، عدد رادیکالی ما \( \Large \sqrt{2} \) است، پس دو ضلع مثلث قائمالزاویه 1 و 1 هستند».
- تعیین جهت حرکت روی محور: اگر علامت قبل رادیکال مثبت باشد، به سمت راست و اگر منفی باشد به سمت چپ مبدأ حرکت میکنیم. «در این مثال، علامت قبل از \( \Large \sqrt{2} \) ، منفی است، پس باید به سمت چپ عدد 1 حرکت کنیم».
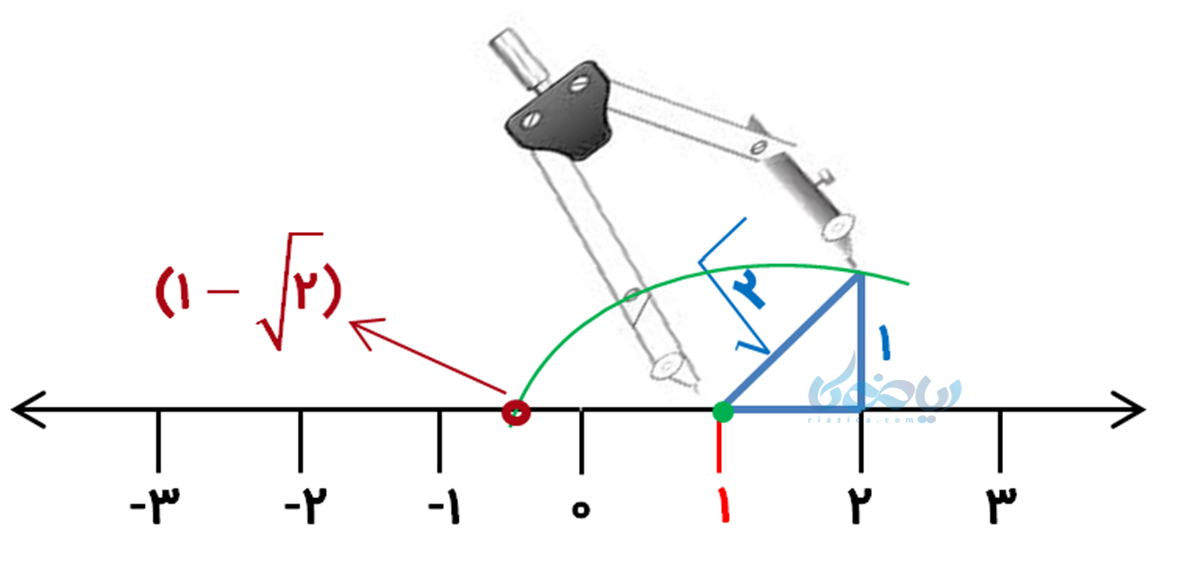
- رسم خط به کمک پرگار: ابتدا و انتهای پرگار را به اندازه عدد رادیکالی (وتر مثلث) باز میکنیم و از مبدأ حرکت، با توجه به جهت مشخص شده روی محور کمان میزنیم. محلی که کمان محور را قطع میکند همان عدد مورد نظر است «در این مثال، ابتدا و انتهای پرگار را روی وتر مثلث به اندازه \( \Large \sqrt{2} \) میگذاریم و از نقطه (1) به سمت چپ کمانی رسم میکنیم تا محور را قطع کند؛ این نقطه همان عدد \( \Large 1- \sqrt{2} \) را نشان میدهد ».
چند مثال برای فهم بیشتر نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم
مثال 2: اعداد \( \Large 1 + \sqrt{2} \) و \( \Large \sqrt{2} – 1 \) را روی محور اعداد نمایش دهید.
حل 2:
برای حل این مثال از همان مراحل نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم استفاده میکنیم. توجه کنید که عدد رادیکالی این مثال، یعنی \( \Large \sqrt{2} \) مشابه نمونه حل شده قبل است؛ اما باید به مبدأ و جهت حرکت توجه نمود.
نمایش عدد \( \Large 1 + \sqrt{2} \):
مبدأ حرکت همان عدد 1 است و با رسم مثلث قائمالزاویهای به اضلاع 1 و 1، به وتری با طول \( \Large \sqrt{2} \) رسیدهایم.
تنها تفاوت آن با نمونه قبل در جهت حرکت است. چون \( \Large \sqrt{2} \) با 1 جمع شده است، این بار کمانی به اندازه \( \Large \sqrt{2} \) را به سمت راست محور رسم میکنیم.
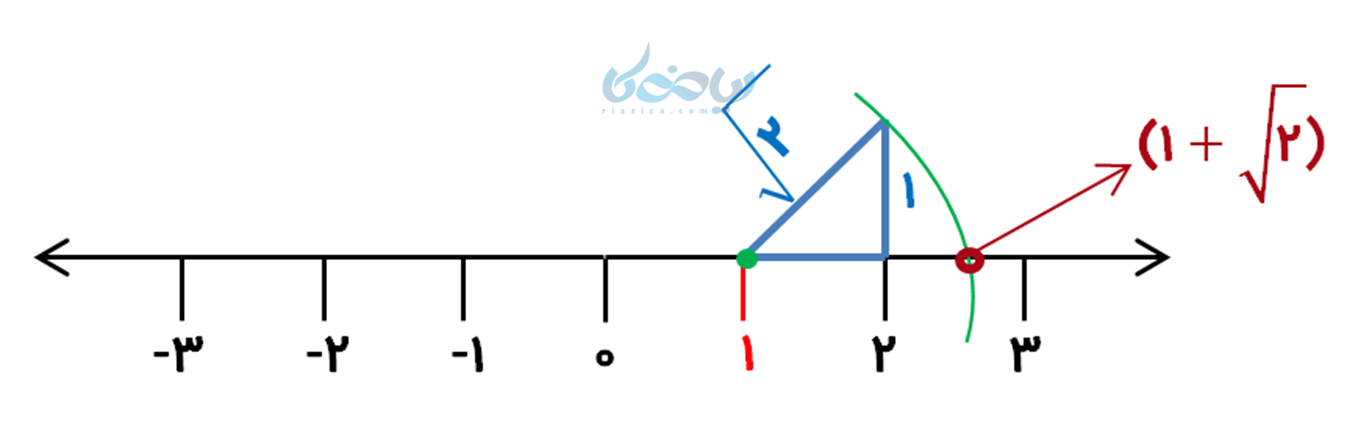
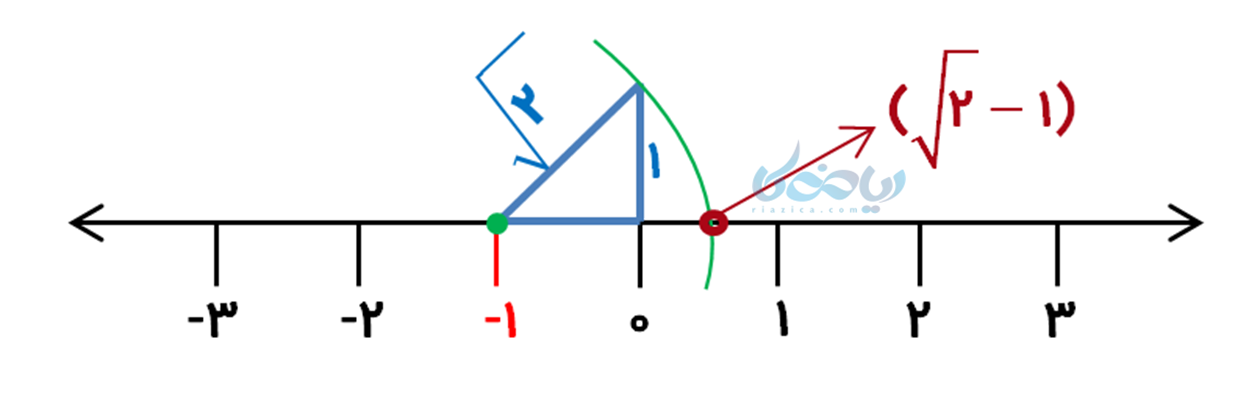
نمایش عدد \( \Large \sqrt{2} – 1 \):
توجه: این عدد را میتوانیم بصورت \( \Large -1 + \sqrt{2} \) بنویسیم. پس مبدأ حرکت عدد (1-) خواهد بود.
این بار از (1-) شروع میکنیم و به طول \( \Large \sqrt{2} \) کمانی به سمت راست محور رسم میکنیم (چون \( \Large \sqrt{2} \) با (1-) جمع شده است). محلی که این کمان محور را قطع کرده است همان عدد\( \Large \sqrt{2} – 1 \) است.
و یک مثال متفاوت
مثال 3: یک محور اعداد رسم کرده و عدد \( \Large 3- \sqrt {13} \) را روی آن نشان دهید.
حل 3:
مرحله به مرحله طبق روش نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم پیش میرویم:
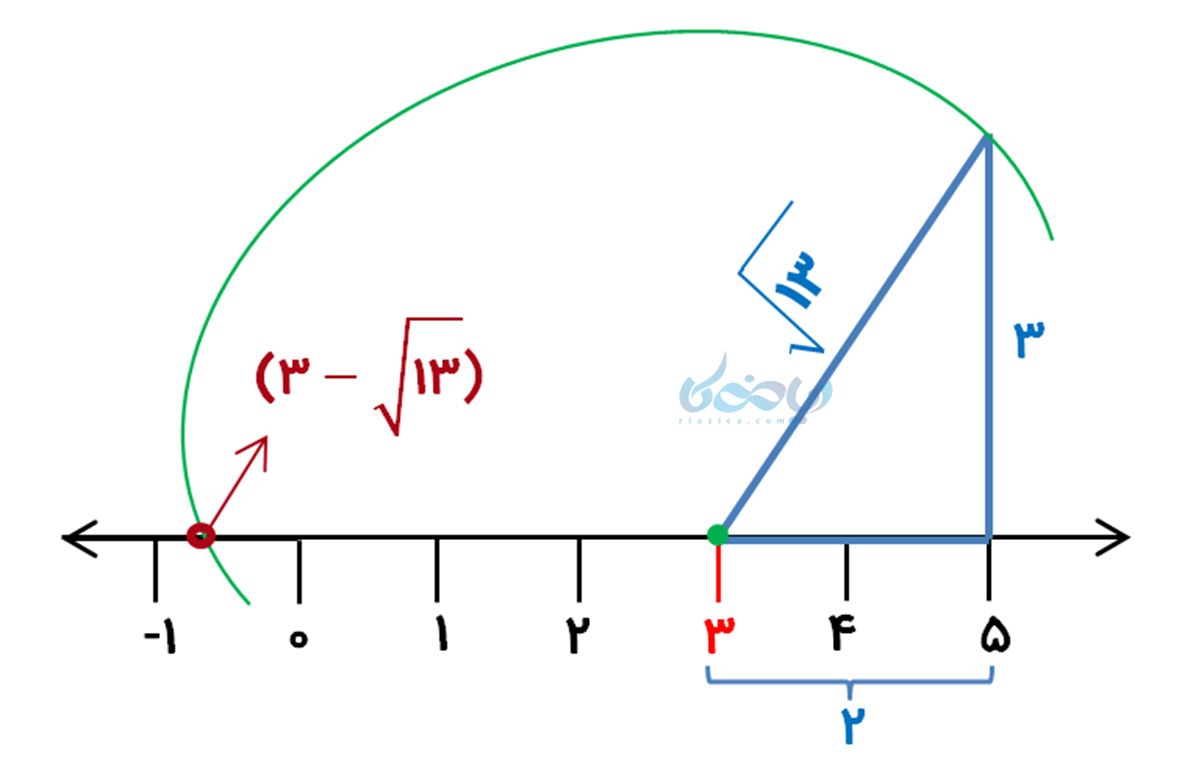
- عدد غیر رادیکالی برابر با (3) است، پس مبدأ حرکت عدد (3) خواهد بود.
- اگر کمی دقت کنیم، جمع مجذورهای 2 و 3 برابر با 13 است؛ یعنی \( 2^2+3^2=13 \) بنابراین از مثلث قائمالزاویهای به اضلاع 2 و 3 استفاده میکنیم.
- علامت قبل از \( \Large \sqrt{13} \) منفی است پس جهت حرکت به سمت چپ محور اعداد خواهد بود.
- سوزن پرگار را روی عدد (3) گذاشته و کمانی به اندازه \( \Large \sqrt{13} \) به سمت چپ محور رسم میکنیم تا محور را در یک نقطه قطع کند. این نقطه نشاندهنده عدد \( \Large 3 – \sqrt{13} \) است.
قسمتی از فایل ویدیویی نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️?
برای خرید نسخه کامل این ویدیو دکمه خرید زیر این فیلم را فشار دهید:
زنگ آخر کلاس نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم
در این محتوا ابتدا با استفاده از مثلث قائمالزاویه و رابطه فیثاغورس یاد گرفتیم که چگونه اندازه یک عدد رادیکالی را رسم کنیم و سپس مرحله به مرحله نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم را آموختیم. مطمئناً با مثالهایی که در این محتوا ارائه شد میتوانیم در ادامه خیلی دقیق اعداد رادیکالها را روی محور نشان دهیم.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاهها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی هشتم به شما پیشنهاد میدهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!





ببخشید رادیکال نه رو چجور ی روی محور نشون می دن ؟
سلام و عرض ادب
رادیکال ۹ برابر با ۳ است.
موفق باشید.
چطوری رادیکال ۸را روی محور رسم کنیم
با سلام وعرض ادب
کافیه مثلثی با ابعاد ۲و۲ رسم کنید وترش میشه رادیکال هشت توصیه میکنم ویدیو مربوط به این قسمت رو تهیه کنید وکامل این بخش رو فرا بگیرید
پیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
با سلام
برای نمایش عدد رادیکال 3روی محور اعداد حقیقی چند بار کمان میزنیم؟
با سلام واحترام دوتا مثلث باید بکشید اما یه کمان میزنید
۲ رادیکال ۳ چطوریه؟
با سلام واحترام
رادیکال سه رو پیدا کنید ودو بار کمان بزنید
با سلام،میتوانید حاصل ۳√۲ را به عدد رادیکالی تبدیل کنید،که برابر است با ۱۲√
سپس عدد ۳√ را روی محور مشخص کنید و بر آن نقطه سه واحد عمود کنید،وتر مثلث شما برابر ۱۲√ خواهد بود،حالا میتوانید کمان بزنید
خداییش دوست عزیز بهش فکر کردی ؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟؟/
رادیکال 9 برابر 3 هست
یه نقطه روی 3 بزن و ایزی ایزی تمام تمام
سلام دوست عزیز
ممنون از پاسخگویی شما
سلام میشه رادیکال 84 هم بدست بیارین با شکل؟
سلام و عرض ادب
این پست را با دقت بخوانید، در انتها سوالی داشتید که نتوانستید کامل رسم کنید، از ما بپرسید.
موفق باشید.
سلام ببخشید در بعضی سوالات مثلث جایش فرق میکند مثلا وتر روی محور هست برای پاسخ چه باید کرد؟!
با عرض سلام واحترام
دوست عزیز شما باید با توجه به غددی که داده شده ضلعهای مثلث رو طوری در نظر بکیری که وتر اون عدد دلخواه بشه پس وتر روی محور قرار تمیگیره
سلام ببخشید یک منهای رادیکال سه رو چجوری روی محور نشان بدم؟
سلام. خوشحالیم که برای یادگیری ریاضی با ما همراه شدید.
اول با روشی که بهتون یاد دادم، رادیکال 2 رو رسم کنید؛ بعد یه پاره خط به طول 1 بر (رادیکال 2) عمود کنید «دقت کنید که لازم نیست همیشه پاره خط ها روی محور باشند»
وتر مثلث جدید، میشه رادیکال 3 … حالا شما می مونید و پرگارتون!!!
اگر ویدئوی این درس رو ببینید، یه مثال شبیه سؤال شما حل شده
سلام
چجوری ۲ به اضافه ی رادیکال ۶ را روی محور نشون بدیم ؟؟
سلام
ببخشید چطوری شکل ۴۷√و۵۰√رو رسم کنیم.
با سلام وعرض ادب
برای رادیکال ۵۰ یه مثلث به اضلاع ۷و۱ رسم کنید
برای رادیکال ۴۷اول یهمثلث به اضلاع ۱و۱ رسم کنید
که وترش میشه رادیکال ۲ وبعد بهش یه ضلع به طول سه عمود کنید وترش میشه رادیکال ۱۱ وبعد یه ضلع به طول ۶ عمود کنید وترش میشه رادیکال ۴۷
سلام.رادیکالِ رادیکال3 چی میشه؟یعنی چه شکلی رو محور مایش داده میشه؟توجه داشته باشید رادیکالِ رادیکال 3 رو می خوام.
چنل ندارید؟؟)
خیلی خوب ودعالی توضیح میدید
سلام و عرض ادب
خوشحالیم که براتون مفید بوده
چنل داریم به همین نام ریاضیکا ویک پیج در اینستا که خیلی فعالتره
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
ممنون:)
چنل ندارید؟؟)!
با سلام
https://t.me/riazica
سلام
رادیکال یک روی محور چطوری میشه؟
با سلام وعرض ادب
رادیکال یک میشه یک، یک هم که مشخصه جاش کجاست.
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام میشه توضیح بدید ۳√ رو چطوری روی محور عداد نشون بدیم و اون رو بنویسیم؟؟؟
با سلام
اینجا نمیشه جواب داد پست رو مطالعه کنید
سلام میشه لطف کنید ۳√ رو روی محور عداد با شکل و جای اون نشون و توضیح بدید؟؟؟ ممنونمیشم ازتون
با سلام و عرض ادب
جواب به این سوالات سخت میشه اگه پست رو دقیق بخونید به جواب سوال میرسید در ویویی همراه این پست خیلی روان وشفاف توضیح داده شد
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام
چجوری عدد رادیکال هفت رو روی محور نشون بدیم؟
با سلام وعرض ادب
مثلثی به ابعاد ۲ورادیکال ۳ نیاز هست برای خود رادیکال ۳ مثلثی به ابعاد ۱ورادیکال ۲ وبرای رادیکال ۲ مثلثی به ابعاد ۱و۱
توصیه میکنم فیلم همراه این پست را حتما ببینید
چگونه تشخیص بدیم ک مثلث در کدوم جهت باشه؟
سلام وعرض ادب
مثلث جهت ندارد
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
چگونه تشخیص بدیم ک جهت مثلث در کدام جهت باشه ؟
با سلام وعرض ادب
مثلث جهت ندارد
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام ببخشید اگر سوال خودش مشخص کرده بود یعنی بت پرگار اندازشو کشیده بآد و گفت کثلا نقطه B چه عدید را نشان میدهد چیکار کنم ؟
با سلام وعرض ادب
دوست عزیز سوالتون مبهم بود ولی با توجه به اونچه من برداشت کردم از روی اعداد نوشته شده روی مثلث ورابطه فیثاغورس باید اندازه وتر رو پیدا کنیم
سلام 4_مثبت رادیکال ۳ روچطور درمحور رسم کنیم
با سلام وروز به خیر
مثلثی به اضلاع رادیکال ۲ و۱ که وترش میشه رادیکال ۳ رسم کنید بعد دهانه پرگار رو یه اندازه رادیکال ۳ باز کرده سوزن رو روی مبدا بذارید به جهت منفی ها ۴ بار کمان بزنید
ببخشید رادیکال 2 مثبت رادیکال 5 را چجوری روی محور نشون بدیم
با سلام واحترام ابتدا مثلث رادیکال دو را بکشید وقتی با پرگار رسمش کردیم از نقطه ای که محور را قطع کرده مثلث رادیکال ۵ رو میکشیم ودوباره با پرگار به اندازه وتر این مثلث کمان میزنیم نقطه بدست آمده جواب شما است
سلام ببخشید تو اون سوال که ۳منهای رادیکال ۱۳ بود چرا از ۳ به طرف مثلا ۵ رفته؟
با سلام واحترام
چون منهای رادیکال سیزده بوده سوزن رو روز ۳ میگذاریم وبه طرف چپ کمان میزنیم اگه بعلاوه رادیکال سیزده بود به طرف راست کمان میزنیم
رادیکال ۷ رو چجوری نشون بدیم؟
با سلام
رادیکال ۷ میشه رادیکال سه بعلاوه ۲ پس یه مثلث با این ابعاد بکشید
ممنون از توضیح عالیتون
با سلام وعرض ادب
ممنون از توجه ونظرات پر انرژی شما
سلام چطور بفهمیم مثلث روی محور چه عددی رو نشون میده
ممنون میشم پاسخ بدیم چون فردا امتحان دارم
با سلام واحترام
از روی اندازه ضلعهای مثلث ورابطه فیثاغورس اندازه ضلع مثلث رو بدست بیارید چون به اندازه وتر کمان زده میشه
عالی بود ممنون از توضیحات کامل و دقیقتون
باسلام واحترام
خدا رو شکر ایتفاده لازم رو بردید فیلم آموزشی این قسمت هم بی نظیر هست
سلام سه منهای رادیکال دو را روی محور نشان دهید
با سلام
دوست عزیز انتظار داری سوال امتحانیت رو اینحا حل کنم ورسم کنم ؟
یکم این مبحث سخته
با سلام وعرض ادب
با تمرین آسون میشه
سلام رادیکال ۲۱ رو چگونه نمایش بدم؟!
با سلام،میتوانید حاصل ۳√۲ را به عدد رادیکالی تبدیل کنید،که برابر است با ۱۲√
سپس عدد ۳√ را روی محور مشخص کنید و بر آن نقطه سه واحد عمود کنید،وتر مثلث شما برابر ۱۲√ خواهد بود،حالا میتوانید کمان بزنید
سلام. چگونه راديكال راديكال دو را روي محور نمايش بدم؟
سلام دوست عزیز
دقیق در داخل پست بالا نشون دادیم مطالعه کنید
سلام ببخشید ۱۱√_۳چجوری روی محور نشون داده میشه
با سلام اول مثلثی به ابعاد یک ودو بکشید تا رادیکال سه به دست بیاد سپس به اون یک ضلع به طول سه عمود کنید تا رادیکال یازده بدست بیاد سوزن پرگار روی روی محورروی عددسه بذارید و به طرف چپ به اندازه رادیکال یازده کمان بزنید
سلام من خرید کلیپ آموزشی نمایش اعداد رادیکالی بر روی محور انجام دادم ولی لینک خرابه و نمیتونم دانلود کنم لطفا پیگیری بفرمایید
سلام
پیگیری شد
سلام چطور رادیکال دو + رادیکال ۵ رو روی محور باید نشون باید داد ؟