آموزش ریاضی پایه هشتم
همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
دوست داری با «دو دو تا چهار تا»ی خودت بفهمی بهترین تیم تاریخ لیگ برتر فوتبال کدومه؟ یا مثلاً نمودار عملکرد درسی خودت رو توی سالهای مختلف ببینی؟ ما خیلی وقتها با اعدادی مثل نمرات درسی، خرج و مخارج زندگی، تعداد کاربران فضای مجازی و … سر و کار داریم که بررسی آنها خیلی به ما کمک میکند. در این آموزش، از مجموعه آموزش ریاضی پایه هشتم ، مفهوم بسیار کاربردی دسته بندی داده ها و جدول فراوانی به ما کمک خواهد کرد تا تعداد زیادی داده آماری را از هم تفکیک کرده و بررسی کنیم؛ اما قبل از آن مروری هم بر انواع نمودارهای آماری خواهیم داشت. حتماً تا آخر مطلب رو بخونید!
یادآوری
تعریف آمار
علم جمع آوری، سازماندهی و تحلیل و تفسیر اطلاعات را علم آمار میگویند. (با این مبحث در پایههای مختلف سر و کار داریم؛ مانند آموزش آمار ریاضی دهم)
تعریف داده آماری
به اطلاعات عددی که جمعآوری میکنیم، داده آماری گفته میشود.
انواع نمودارها و کاربردهای آنها
انواع نمودار دادههای آماری شامل موارد ذیل میباشد:
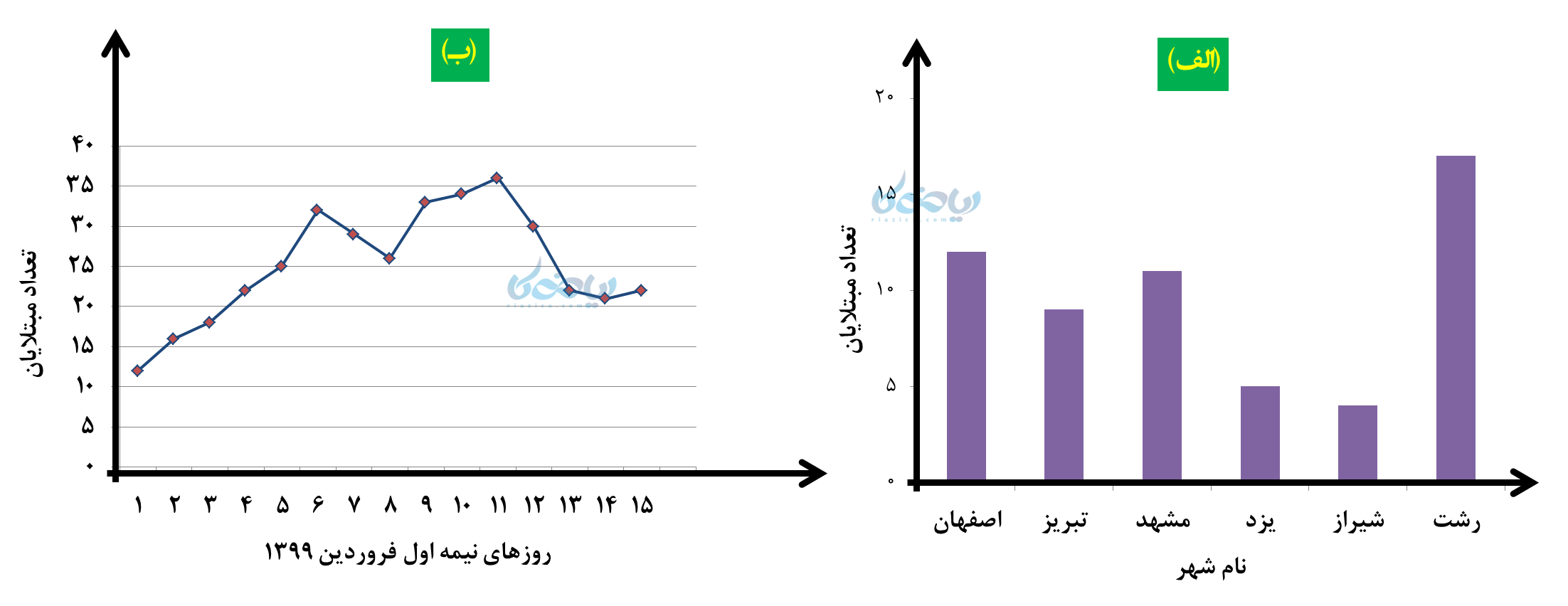
- نمودار میلهای: برای مقایسه تعداد و مشخص کردن کمترین و بیشترین داده آماری
- نمودار خط شکسته: برای نشان دادن تغییرات در مدتی مشخص
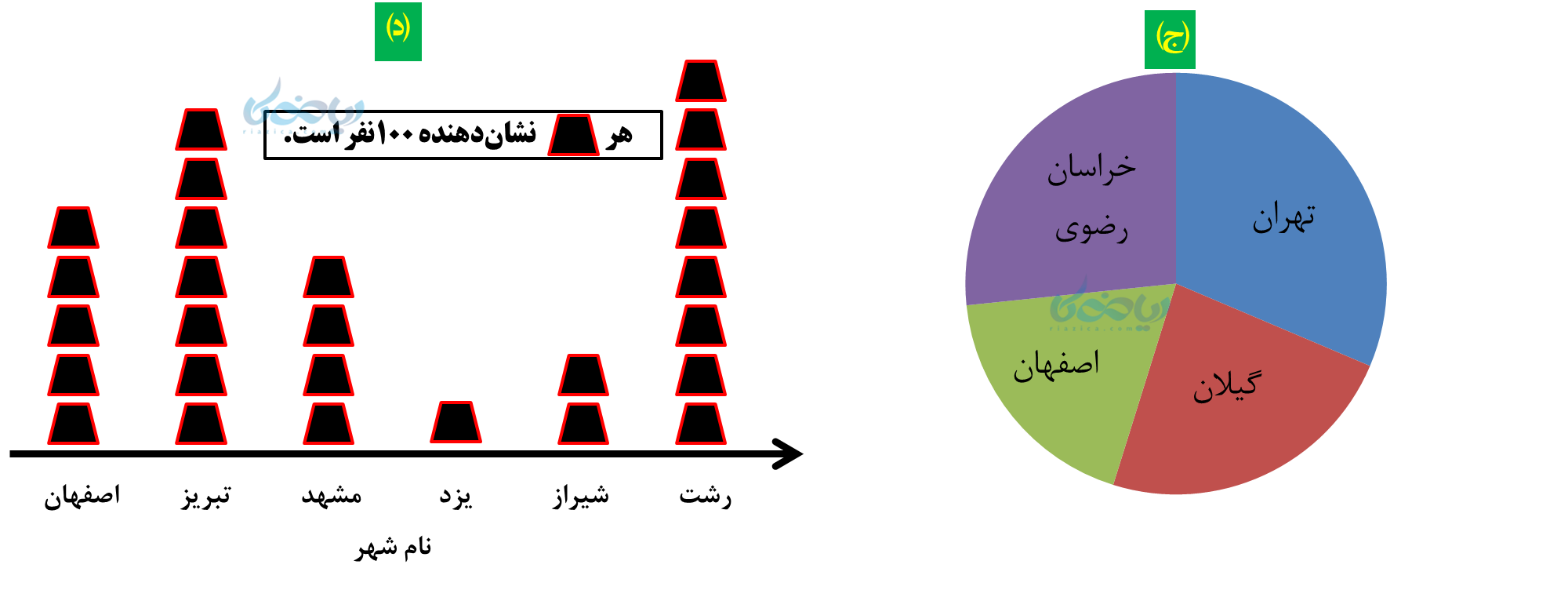
- نمودار تصویری: برای نشان دادن یک تعداد مشخص از دادهها با تصویر
- نمودار دایرهای: برای نشان دادن تعداد دادهها نسبت به کل
برای روشنتر شدن مفهوم نمودارها به مثالهای مفهومی زیر در مورد ویروس کرونا توجه کنید:
دسته بندی داده ها – شاهراه رسیدن به جدول فراوانی
هنگام کار با دادههای آماری، ممکن است با تعداد داده بسیار زیاد مواجه شوید. مثلاً آیا میتوانید وضعیت نمرات درس زبان انگلیسی یک مدرسه بزرگ 200 نفری را تک تک بررسی کنید؟ قطعاً نه!
چگونه میتوانیم این همه داده پراکنده را که جمعآوری شده است بررسی کنیم و به نتیجه برسیم؟ با دسته بندی داده ها متناسب با موضوع آماری و تشکیل جدول فراوانی آن.
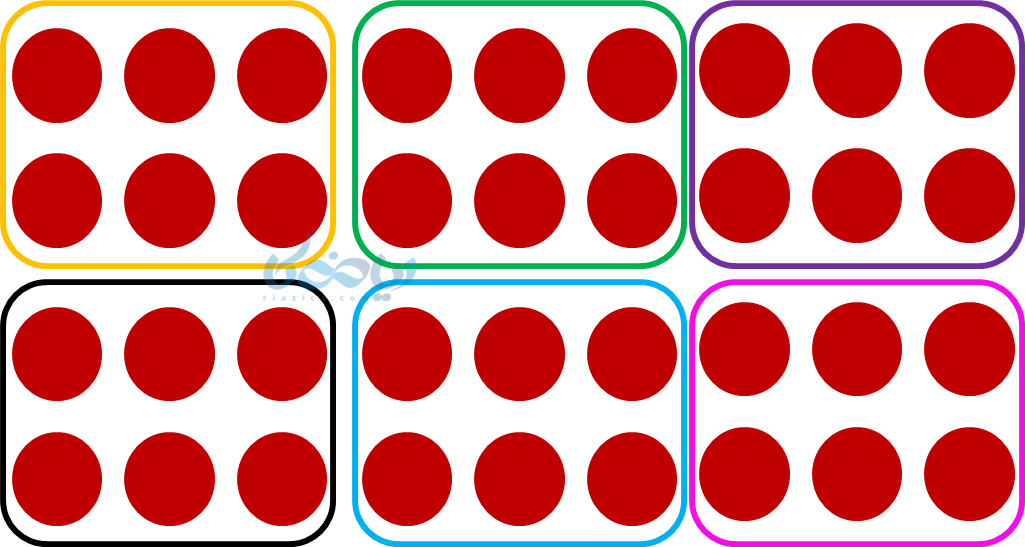
به عنوان مثال در یک بررسی آماری با تعداد 36 داده، میتوان 6 دسته داشت که هر کدام 6 داده دارند؛ با تعاریف و روشهایی که در ادامه یاد میگیرید، آنها را بررسی کرده و برای آنها جدول فراوانی تشکیل میدهیم.
تعاریف
دامنه تغییرات
اختلاف بزرگترین و کوچکترین داده آماری را دامنه تغییرات میگویند.

طول دسته
اختلاف بزرگترین و کوچکترین داده در یک دسته را طول دسته میگویند.

میانگین
میانگین، همانطور که در سالهای قبل یاد گرفتهاید، متوسط دادههاست که از تقسیم مجموع دادهها به تعداد آنها محاسبه میشود.

مرکز دسته
میانگین بزرگترین و کوچکترین دادههای یک دسته میباشد که از تقسیم جمع این دو داده تقسیم بر 2 بدست میآید.

فراوانی
تعداد دادههای هر دسته را فراوانی میگویند.
جدول فراوانی
جدولی شامل طول دسته ها، فراوانی هر دسته و مرکز دسته، که در ادامه بررسی خواهد شد.
مثال 1: در یک کلاس درس 14 نفری، معلم گروههای علمی تشکیل داده و اعلام کرده است به بالاترین میانگین نمرات گروهی، جایزه میدهد. نمرات و گروهبندی دانشآموزان به این صورت است:
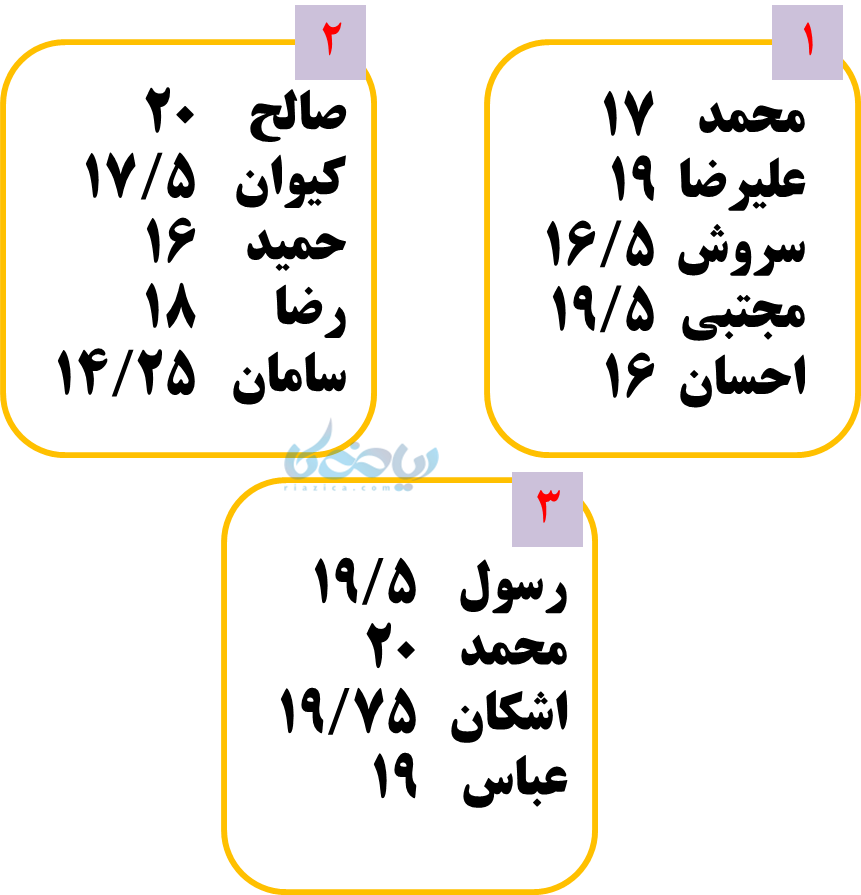
دامنه تغییرات، طول هر دسته، میانگین کل، مرکز هر دسته و فراوانی دستهها را بدست آورید. کدام گروه برنده جایزه میشوند؟ در کدام گروه دانشآموزان از لحاظ نمره به هم نزدیکترند؟
حل 1:
برای بدست آوردن دامنه تغییرات، باید بزرگترین و کوچکترین داده را مشخص کنیم (در کل دادهها): 20 و 14/25، پس دامنه تغییرات برابر است با: \( \Large 20 – 14/25 = 5/75\)
برای محاسبه طول هر دسته، از تفاضل بیشترین و کمترین نمره هر گروه استفاده میکنیم:
- طول دسته 1: \(\Large 19/5{\rm{ }} – 16 = 3/5\)
- طول دسته 2: \(\Large 20 – 14/25 = 5/75\)
- طول دسته 3: \(\Large 20 – 19 = 1\)
میانگین نمرات کل کلاس:
برای محاسبه مرکز هر دسته بزرگترین و کوچکترین نمره هر گروه را با هم جمع کرده و به 2 تقسیم میکنیم:
\(\Large \begin{array}{l}\overline {\rm{x}} = \frac{{\rm{S}}}{{\rm{N}}}\\\overline {\rm{x}} = \frac{{17 + 19 + 16/5 + … + 19/75 + 19}}{{14}}\\\overline {\rm{x}} = 18\end{array}\)
- مرکز دسته 1: \( \Large \frac{{19/5 + 16}}{2} = 17/75\) ؛
- مرکز دسته 2: \(\Large \frac{{20 + 14/25}}{2} = 17/125\) ؛
- مرکز دسته 3: \(\Large \frac{{20 + 19}}{2} = 19/5\) .
فراوانی دسته، همان تعداد دادههای هر گروه است:
- فراوانی دسته 1: 5 عدد
- فراوانی دسته 2: 5 عدد
- فراوانی دسته 3: 4 عدد.
گروهی برنده چایزه است که بهترین میانگین را داشته باشد. پس میانگین هر گروه را محاسبه میکنیم:
- میانگین گروه 1: \(\Large {\overline {\rm{x}} _1} = \frac{{17 + … + 16}}{5} = 17/6\)
- میانگین گروه 2:\(\Large {\overline {\rm{x}} _2} = \frac{{20 + … + 14/25}}{5} = 17/15\)
- میانگین گروه 3: \(\Large {\overline {\rm{x}} _3} = \frac{{19/5 + … + 19}}{4} = 19/56\)
بنابراین گروه 3 با میانگین بالاتر برنده جایزه خواهد بود.
حال میتوانیم موارد بدست آمده را به شکل جدول هم دستهبندی کنیم:
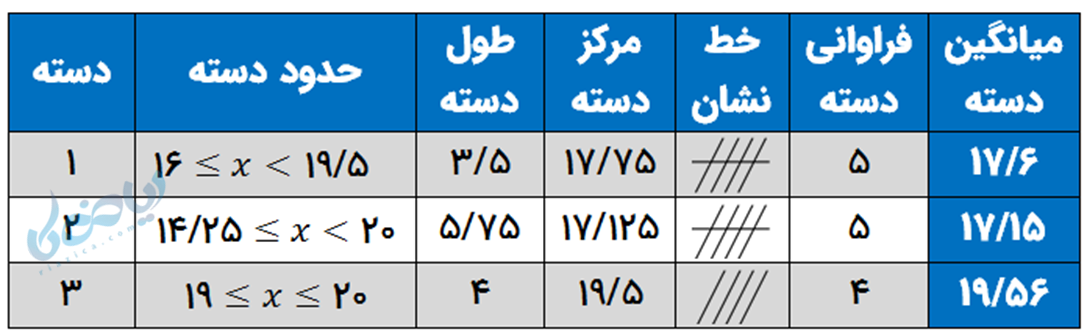
طول دسته، معیاری برای نزدیک بودن دادهها در دسته بندی داده ها:
برای پاسخ به سؤال در مورد این که کدام گروه از لحاظ نمره به هم نزدیکتر بودهاند، میتوان از طول دسته استفاده کرد؛ چون نشان میدهد بهترین و بدترین نمره چقدر فاصله دارند. در این مورد، گروه 3 با طول دسته 1 بهترین عملکرد را داشتهاند.
مثال 2: اگر میانگین 5 نمره درسی شما 17/5 باشد، با گرفتن نمرههای 19 و 15 در دو آزمون بعدی وضعیت نمره شما بهتر خواهد بود یا خیر؟
حل 2:
میانگین 5 نمره درسی شما 17/5 بوده است؛ بنابراین طبق فرمول میانگین \( \Large \overline {\rm{x}} = \frac{{\rm{S}}}{{\rm{N}}} \to 17/5 = \frac{{\rm{S}}}{5}\) مجموع نمرات او (S) برابر است با: \( \Large {\rm{S = }}5 \times 17/5 = 87/5 \)
برای تعیین وضعیت، باید میانگین قبلی و میانگین جدید را با هم مقایسه کرد. برای بدست آوردن میانگین جدید:
\( \Large \overline {\rm{x}} = \frac{{\rm{S}}}{{\rm{N}}} = \frac{{87/5 + 19 + 15}}{7} \)
\( \Large \overline {\rm{x}} = \frac{{121/5}}{7} \simeq 17/35 \)
به دلیل کاهش میانگین، نمره او کاهش یافته است.
روش دسته بندی داده ها و تشکیل جدول فراوانی
در این بخش ابتدا روند کلی دسته بندی داده ها و تشکیل جدول فراوانی را مرور کرده و پس از آن، این موارد را در مثال بکار میگیریم. برای دسته بندی داده ها تا رسیدن به جدول فراوانی مراحل زیر را طی میکنیم:
- دامنه تغییرات دادهها را بدست میآوریم.
- با تقسیم دامنه تغییرات به تعداد دستههای مورد نظر، طول هر دسته را محاسبه میکنیم. (طول دستهها برابرند.)
- بر اساس طول دسته بدست آمده در مرحله قبل، دادهها را به بازههای مساوی با طول دسته تقسیم میکنیم.
- دادهها را با توجه به بازههای موردنظر، در دستهبندیها قرار میدهیم.
- فراوانی هر دسته را با شمارش دادههای هر دسته (بازه) بدست میآوریم. (میتوان برای شمارش تعداد دادهها از خط نشان استفاده کرد.)
- مرکز دستهها را تعیین میکنیم.
- هر دسته را در یک سطر از جدول فراوانی قرار داده و حاصلضرب مرکز دسته در فراوانی را برای هر کدام محاسبه میکنیم.
- در صورت نیاز، نمودار فراوانی را نیز رسم میکنیم. در این نمودار، محور افقی طول دستهها و محور قائم فراوانی میباشد.
تذکر: بازه عددی هر دسته بدین صورت است: ؛ یعنی عدد انتهایی مربوط به دسته بعدی است؛ به جز در دسته آخر که عدد انتهای بازه هم جزو دسته است.
محاسبه میانگین به کمک جدول فراوانی
زمانی که تعداد دادهها زیاد باشد، استفاده از فرمول گفته شده در بخش قبل، بسیار زمانبر خواهد بود.
در چنین شرایطی میتوان ابتدا مطابق مراحل گفته شده در قسمت قبل، جدول فراوانی را تشکیل داد و سپس از فرمول زیر برای محاسبه میانگین کل دادهها استفاده کرد:

در واقع در این فرمول، جهت کاهش محاسبات، مرکز هر دسته به عنوان میانگین دسته در نظر گرفته شده است.
مثال 3: نمرات ریاضی 30 دانشآموز به صورت زیر میباشد:
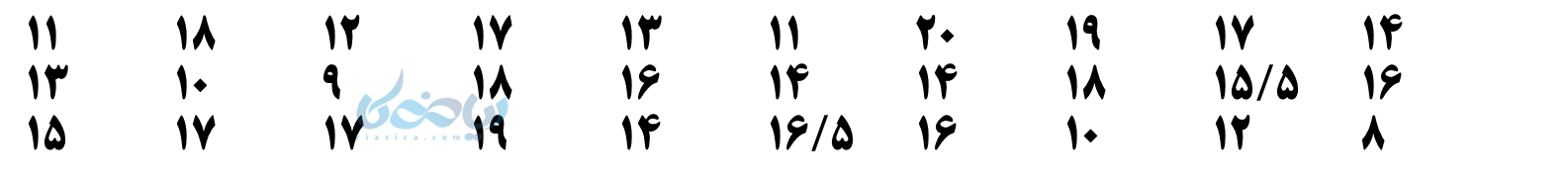
با دسته بندی داده ها در 3 دسته، میانگین نمره کلاس را بدست آورده و نمودار فراوانی آن را رسم کنید.
حل 3:
مشاهده میشود که بیشترین و کمترین داده به ترتیب 20 و 8 است. مراحل زیر را طی میکنیم:
مراحل حل 3:
مراحل زیر را برای رسیدن به پاسخ طی میکنیم:
-
- با تقسیم دامنه تغییرات به تعداد دستهها، طول هر دسته محاسبه میشود: \(\Large \frac {12}{3}= 4 \).
- نمرات 8 الی 12 را به حدود دستههایی با طول 4 تفکیک میکنیم؛ مطابق ستون اول (به باز و بسته بودن بازه دقت کنید- مثلاً عدد 12 متعلق به دسته دوم است، نه دسته اول). دسته اول: عدد اول 8 و طول دسته 4 است، پس عدد انتهای دسته اول برابر است با \(\Large 8+4=12 \) (عدد 12 مربوط به دسته بعدی است) پس حدود دسته \( 8≤x<12 \) است؛ دسته دوم: عدد اول 12 و طول دسته 4 است، پس عدد انتهای دسته دوم برابر است با \(\Large 12+4=16 \) (عدد 16 مربوط به دسته بعدی است) پس حدود دسته
- \( 12≤x<16\) است؛ دسته سوم: عدد اول 16 و طول دسته 4 است، پس عدد انتهای دسته اول برابر است با \( 16+4=20 \) (عدد 20 مربوط به همین دسته است؛ چون دسته آخر است) پس حدود دسته \( 16≤x≤20 \) است.
- با توجه به بازههای مشخص شده در جدول، تعداد نمرات هر بازه را شمارش میکنیم و خط نشان میکشیم و همچنین در قسمت فراوانی آن تعداد را ثبت میکنیم.
- مرکز دستهها با توجه به حدود دستهها تعیین میشود (در اینجا بر خلاف بند 2 به باز یا بسته بودن بازه توجه نکنید). مرکز دسته اول، میانگین اعداد 8 و 12 است، یعنی \( \Large \frac {8+12}{2}= 10 \) ؛ مرکز دسته دوم میانگین اعداد 12 و 16 است، یعنی \( \Large \frac {12+16}{2}= 14 \) ؛ مرکز دسته سوم، میانگین اعداد 16 و 20 است، یعنی \(\Large \frac {16+20}{2}= 18 \) .
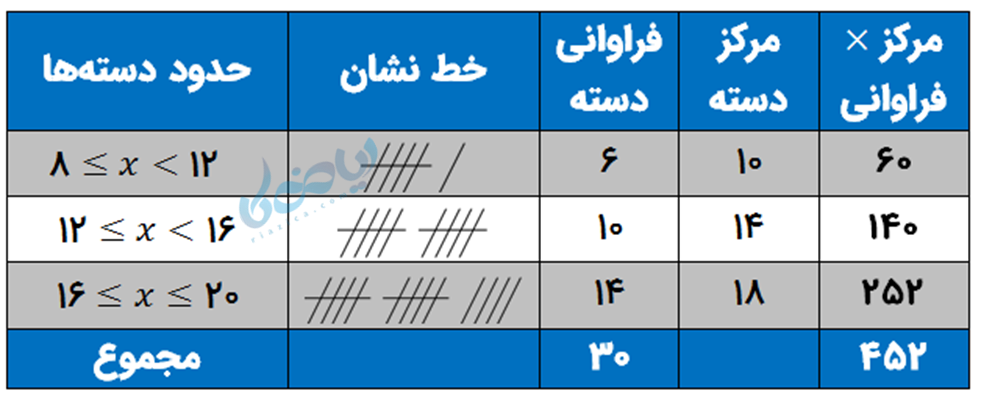
میانگین نمرات کلاس، از تقسیم (مجموع حاصلضرب فراوانی در مرکز دسته) بر (مجموع فراوانیها = تعداد دادهها) بدست میآید:
\( \Large \overline {\rm{x}} = \frac{{452}}{{30}} \simeq 15/07 \)
همچنین نمودار فراوانی آن به این صورت خواهد بود:
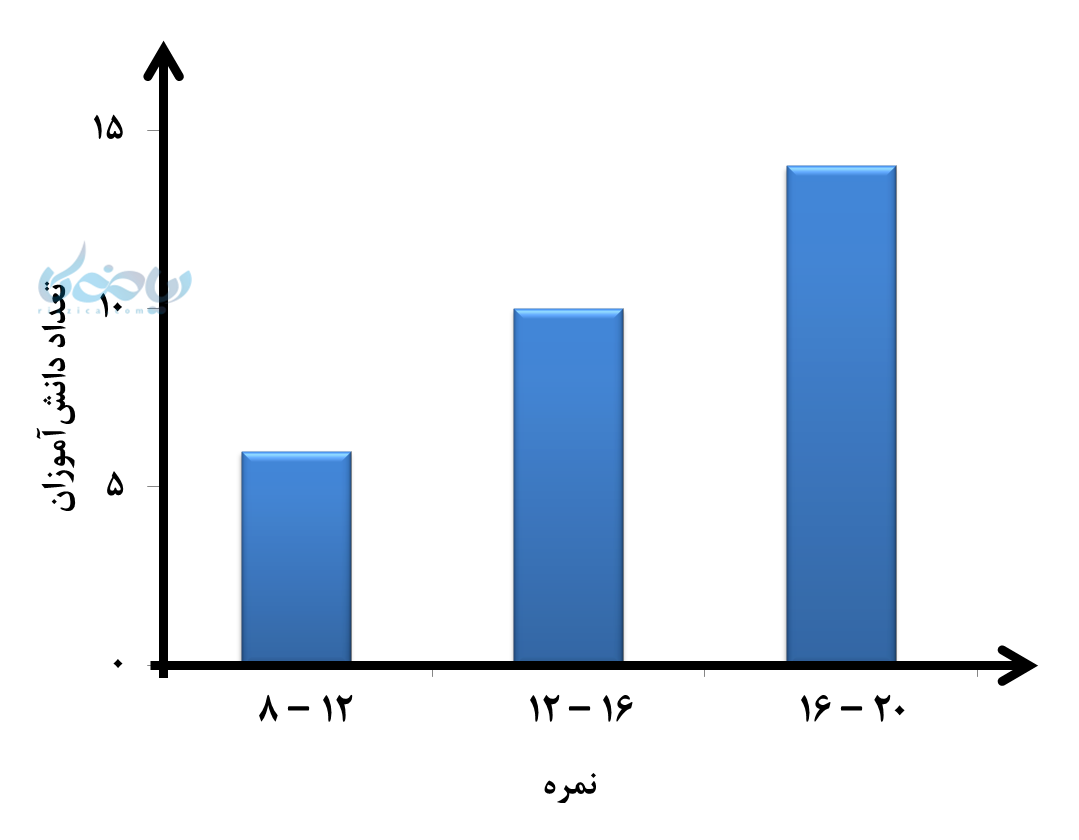
ویدیو جدول فراوانی ریاضی هشتم
در این ویدیو مبحث جدول فراوانی ریاضی هشتم را با مثالهای ملموس یاد می گیرید
زنگ آخر کلاس جدول فراوانی
در این درسنامه مهم، یاد گرفتیم که چگونه با یک سری مراحل ساده مانند محاسبه دامنه تغییرات و طول دسته، تعداد زیادی داده آماری را دسته بندی کنیم و برای آنها جدول فراوانی تشکیل دهیم.
با این روش اکنون میتوانیم میانگین را در بررسی حجم زیادی از دادههای پراکنده بدست آوریم. حالا به راحتی میتونی با میانگینگیری ببینی مثلاً توی کدوم مقطع تحصیلی عملکرد بهتری در درس ریاضیات داشتی.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاهها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامههای آموزش ریاضی هشتم به شما پیشنهاد میدهیم:
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خط و دایره : از سیر ➖ تا پیاز 🔴
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!





ممنون عالی بود
ضمن عرض سلام
سپاسگزاریم از لطف شما دوست عزیز
تو ویدیو آموزشی تون در قسمت مرکز دسته ضرب در فراوانی جواب
12×6 رو 32 نوشتید ولی 72 میشه
ممنون از دقت نظر شما
سلام من سوال داشتم
چرا مرکز دسته رو بدست میارم ؟ و بعد ضرب در فراوانی میکنیم ؟ داستانش چیه؟ و اینکه چرا با این کار ها بازم جواب تقریبی درمیاد؟
با سلام واحترام
مرکز دسته میانگین اعداد موجود در هر دسته را نشان میدهد ووقتی ضرب فراوانی میشود فراوانی تقریب هر دسته را نشان میدهد درسته که جوابها تقریبی است ولی مقدار خطا کم است وبرای برنامه ریزیها در تحقیقات کافیست
این رو باید چطوری بخونیم؟
4≥x≥صفر
با سلام وعرض ادب
میخوانیمایکس بین صفر وچهار یا مساوی صفر وچهار یا اینک میگوییم ایکس بزگتر مساوی صفر وکوچکتر مساوی ۴
این رو باید چطوری بخونیم؟
4≥x≥صفر
با سلام وعرض ادب
میخوانیم ابکس بین صفر وچهار یا مساوی صفر وچهار یا اینک میگوییم ایکس بزگتر مساوی صفر وکوچکتر مساوی ۴
\
سلام ببخشید در عمل جمع کردن اختلاف نمرات پایین تر از میانگین با بالای میانگین چه چیزی حاصل میشود؟
با سلام
اگر این مقادیر را جمع وبه توان دو برسانده و تقسیم بر تعداد داده ها کنیم انحراف معیار یا همان پراکندگی داده مشخص می شود
سلام وقتی اعداد را مشخص نمیکنند فقط کمترین و بیشترین عدد را می دهند فراوانی را چگونه محاسبه میکنند؟ ممنون
با سلام وعرض ادب
باید سوال واطلاعات سوال رو دید اینکه شما میگید فقط دامنه تغیرات بدست می آید
فراوانی و چجور باید بدست بیاریم؟? واقعن واسم سوال شدع ?
با سلام وروز به خیر
از روی صورت سوال تعداد داده های هر دسته را مشمارید مثلا نمرات ۱۶ تا بیست را برای دسته آخر میشمارید البته خود ۱۶ روحساب نکنید
سلام وقتی سوال نمرات ی کلاسی و دادع و از ما جدول فراوانی میخاد چجور فراوانی و بدست بیاریم؟ ?
سلام ممنون بابت توضیحات خوبتون??
سلام
سلام دوست عزیز
سلام ببخشید من بازم فراوانی رو نفهمیدم میشه دقیق تر توضیح بدین با مثال ممنون میشم.
با سلام
فراوانی یعنی تعداد داده های هر دسته
داده یعنی اون اعداد وارقامی که میئله به ما داده
فراوانی
ممنون بابت سایت عالیتون
با سلام وعرض ادب
واقعا خوشحالیم از این همه پیامهای پر انرژی شما
احسند
ممنون انشالله که مشکلتون رفع شده باشه
سلام ممنون بابت توضیحات خوبتون??
با سلام وعرض ادب
خواهش میکنم خوشحالیم که مفید بوده
سلام خسته نباشید ببخشید چطوری فروانی بدست می آید
با سلام از روی صورت مسئله داده ها رو میشمریم
سلام
منظور از درصد فراونی چیه ؟
با سلام
فراونی تقسیم بر صد
خیلی عالی
سلام خسته نباشید ببخشید چطوری فروانی بدست می آید
سلام خسته نباشید
سپاس از توضیحاتتون ?✨
ببخشید اگر به ما فقط دسته را داده بود و ما با استفاده از آن ور کز دسته را بدست آورده باشیم چگونه می توانیم فراوانی را بدست آوریم ؟
سلام خسته نباشید وقتی داخل جدول فقط دسته و مرکزدسته × فراوانی رو به ما داده باشه و خط نشان و فراوانی و مرکز دسته رو نداشته باشیم چطوری جدول رو حل کنیم؟
سلام خسته نباشید
میخواستم بپرسم که دسته فراوانی چگونه به وجود میاد و اینکه چگونه از دسته ها فراوانی بدست بیارم ممنون میشم
عالی بود
سلام
چگونه باید حدود دسته را بدست بیاریم
معمولا در سوال تعداد دسته خواسته شده دامنه تغییرات را به تعداد دسته تقسیم میکنیم طول دسته بدست می آید بعد با توجه به آن از کوچکترین داده شروع وحدود دسته را مشخص می کنیم
سلام خسته نباشید ممنون بابت مطالب مفیدتون یک سوال داشتم وقتی به ما خط نشان رو نداده باشند ما چطور باید فراوانی رو بدست بیاریم؟
سلام حدود دسته چیه میشه توضیح بدین
با سلام
پست رو بخونید منوجه می شوید .
ریاضی