آموزش ریاضی پایه هفتم
عبارت های جبری هفتم 🆎🆗 – ساده سازیش کن!
در درسنامۀ عبارت های جبری هفتم به سؤالات زیر پاسخ میدهیم:
- “جمله” در یک عبارت جبری چیست؟
- عبارتهای متشابه کدامند؟
- جمع و تفریق و ضرب و تقسیم عبارتهای جبری چگونه است؟
در انتهای درسنامۀ الگوهای عددی ریاضی هفتم با عبارتهای جبری آشنا شدیم. این بار میخواهیم کمی جامعتر، عبارتهای جبری و نحوۀ رفتار آنها را مورد بررسی قرار دهیم. ابتدا چند مثال از عبارتهای جبری هفتم میبینیم، سپس به سؤالاتی که در ابتدای درسنامه پرسیدیم پاسخ خواهیم داد.
مثال از عبارتهای جبری
مثال 1: مساحت هر یک از مثلثهای زیر را بیابید.
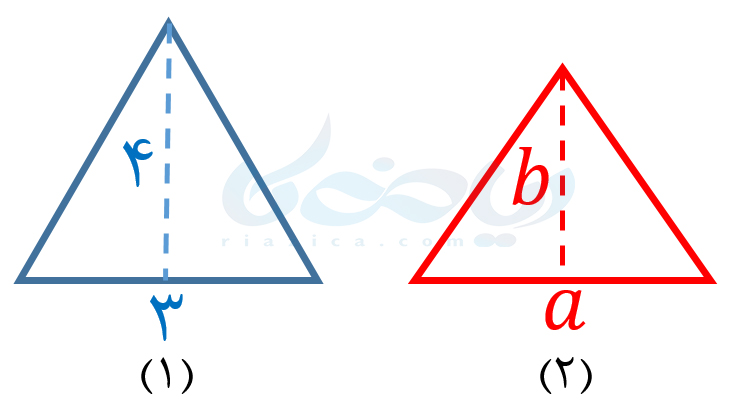
حل: مساحت مثلث برابر است با اندازۀ قاعده ضرب در ارتفاع. بنابراین مساحت مثلث (1) برابر است با:
\( \LARGE S_1=\frac{3\times 4}{2}=6\)
برای محاسبۀ مساحت مثلث (2) نیز باید قاعده را ضرب در ارتفاع کنیم. بنابراین مساحت مثلث (2) برابر است با:
\( \LARGE S_2=\frac{a\times b}{2}\)
همانطور که در درسنامۀ الگوهای عددی ریاضی هفتم گفتیم، در عبارت بالا، \(\Large a\) و \(\Large b\) دو متغیر هستند. به عبارتهایی که شامل متغیرها و اعمالی مانند جمع و تفریق یا ضرب و تقسیم بین آنها هستند، عبارتهای جبری میگوییم. معمولاً در عبارتهای جبری، ضرب را با نقطه نمایش دهیم یا اینکه برای نمایش آن از هیچ علامتی استفاده نمیکنیم. مثلاً مساحت مثلث (2) را میتوان به صورت \( \Large S_2=\frac{ab}{2}\) یا \( \Large S_2=\frac{a.b}{2}\) یا \( \Large S_2=\frac{(a)b}{2}\) یا \( \Large S_2=\frac{a(b)}{2}\) نیز نشان داد. در قسمت بعدی از درسنامۀ عبارت های جبری هفتم به مفهوم جمله در عبارتهای جبری میپردازیم.
جمله در عبارتهای جبری
ابتدا یک مثال از عبارتهای جبری میبینیم و سپس مفهوم جمله جبریرا توضیح میدهیم.
مثال 2: در یک فروشگاه سازهای ایرانی، قیمت هر ساز عود برابر با \(\Large a\) و قیمت هر ساز رباب برابر با \(\Large b\) است. اگر بخواهیم برای یک آموزشگاه موسیقی، هشت ساز عود و پنج ساز رباب تهیه کنیم، چه هزینهای باید بپردازیم؟
حل: با توجه به اطلاعات مسئله، قیمت هشت ساز عود برابر با \(\Large 8a\) و قیمت پنج ساز رباب برابر با \(\Large 5b\) است. بنابراین مجموع هزینهای که آموزشگاه باید بپردازد برابر است با:
\(\LARGE 8a+5b\)
در عبارت بالا، \(\Large 8a\) یک جمله است. \(\Large 5b\) نیز یک جمله است. اگر یک عدد بدون متغیر نیز داشتیم، یک جمله به حساب میآمد. مثلاً عبارت \(\Large a+3b+2\) را در نظر بگیرید. \(\Large a\) یک جمله، \(\Large 3b\) یک جمله و \(\Large 2\) نیز یک جمله است. یعنی عبارت \(\Large a+3b+2\) از سه جمله تشکیل شده است.
برای یادگیری مفهوم دقیق تر جمله جبری ویک جمله ایها وچند جمله ایها به پستهای ساده کردن عبارتهای جبری هشتم و تابع چند جمله ای دهم مراجعه کنید
در قسمت بعدی از درسنامۀ عبارت های جبری هفتم ، به این سوال پاسخ میدهیم که چه زمانی دو جمله متشابه هستند.
جملات متشابه در عبارت های جبری هفتم
زمانی که با مفهوم توان آشنا شوید، میتوانیم تعریف مناسبی از جملات متشابه ارائه دهیم. فعلاً سعی میکنیم با مثال، این مفهوم را یاد بگیریم. دو جملۀ \(\Large 2a\) و \(\Large 5a\) متشابهاند. دو جملۀ \(\Large 4b\) و \(\Large 7b\) نیز متشابهاند. اما به طور مثال، جملات \(\Large 2a\) و \(\Large 4b\) متشابه نیستند. یا مثلاً جملات \(\Large 3a\) و \(\Large 2\) متشابه نیستند. برای سادهسازی یک عبارت جبری، جملات متشابه را با هم ساده میکنیم. یعنی جمع و تفریق یا ضرب و تقسیم جملات متشابه را با هم انجام میدهیم. همچنین، از قوانینی مانند شرکتپذیری یا جابجایی که برای اعداد استفاده میکردیم، برای عبارتهای جبری نیز میتوانیم استفاده کنیم. برای اینکه بهتر متوجه شوید، به مثالهای زیر از درسنامۀ عبارت های جبری هفتم توجه کنید.
مثال از ساده کردن عبارتهای جبری
مثال 3: عبارت جبری \(\Large (2x+3)+(5x+6)\) را ساده کنید.
حل: همانطور که گفتیم باید جمع و تفریق یا ضرب و تقسیم جملات متشابه را با هم انجام دهیم. جملات \(\Large 2x\) و \(\Large 5x\) باهم متشابهند پس ضرایبشان را با هم طبق علامتشان جمع میکنیم و جملات \(\Large 3\) و \(\Large 6\) با هم متشابهاند. بنابراین داریم:
\(\Large (2x+3)+(5x+6)\)
\(\Large =(2x+5x)+(3+6)\)
\(\Large =7x+9\)
به مثال بعدی از درسنامۀ عبارت های جبری هفتم توجه کنید.
مثال 4: عبارت جبری \(\Large 3x+2+4y-5x+6y-3\) را ساده کنید.
حل: جملات \(\Large 3x\) و \(\Large -5x\) با هم، جملات \(\Large 4y\) و \(\Large 6y\) با هم و جملات \(\Large 2\) و \(\Large -3\) با هم متشابهاند. بنابراین داریم:
\(\Large 3x+2+4y-5x+6y-3\)
\(=(3x-5x)+(4y+6y)+(2-3)\)
\(\Large =-2x+10y-1\)
ضرب یک عدد در پرانتز در عبارت های جبری هفتم
مورد بعدی که در درسنامۀ عبارت های جبری هفتم بررسی میکنیم، ضرب یک عدد در پرانتز است. برای ساده کردن عباراتی که شامل ضرب یک عدد در پرانتز میشوند، از قاعدۀ پخشی استفاده میکنیم. مثال زیر را در نظر بگیرید.
مثال 5: عبارت جبری \(\Large 4(2x-8)\) را ساده کنید.
حل: همانطور که گفتیم باید از قاعدۀ پخشی استفاده کنیم. یعنی باید \(\Large 4\) را در هر یک از جملات پرانتز ضرب کرده و سپس حاصل را از هم کم کنیم:
\(\Large 4(2x-8)\)
\(\Large =(4\times 2x)-(4\times 8)\)
\(\Large =8x-32\)
علامت منفی پشت پرانتز در عبارت های جبری هفتم
و اما نکتۀ آخر درسنامۀ عبارت های جبری هفتم در مورد علامت منفی پشت یک پرانتز است. زمانی که یک علامت منفی پشت یک پرانتز قرار میگیرد، روی تمام عبارتهای موجود در پرانتز اثر میگذارد. به عبارت دیگر، تمام عبارتهای موجود در پرانتز، قرینه میشوند. به مثال زیر توجه کنید.
مثال 6: عبارت جبری \(\Large (3x+5)-(2x-4)\) را ساده کنید.
حل: همانطور که گفتیم، علامت منفی پشت پرانتز \(\Large (2x-4)\) هم \(\Large 2x\) را قرینه میکند و هم \(\Large -4\) را قرینه میکند. بنابراین داریم:
\(\LARGE (3x+5)-(2x-4)\)
\(\LARGE =3x+5-2x+4\)
\(\LARGE =x+9\)
مثال ۷: عبارت های جبری متشابه را در تصویر زیر مشخص کنید.
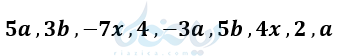
حل:
![]()
جملات همرنگ متشابهند .
برای ادامه مطلب پست مقدار عددی یک عبارت جبری رو مطالعه کن.
ویدیو آموزشی از عبارت های جبری هفتم
در این ویدیو شما آموزشی کامل از عبارت های جبری هفتم همراه مثالهای فراوان مشاهده میکنید.
زنگ آخر کلاس عبارت های جبری هفتم
به پایان این درسنامه رسیدیم. هدف این درسنامه، آموزش ساده سازی عبارتهای جبری بود. برای رسیدن به این هدف، ابتدا جمله را تعریف کردیم. سپس دیدم که چه جملههایی در یک عبارت جبری متشابه هستند. در نهایت روش ساده سازی عبارتهای جبری را با توجه به جملات متشابه بررسی کردیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث عبارت های جبری هفتم دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.





خیلی توضیح جامع و عالیی بود?? اگر آزمون های آنلاین هم برای خود ارزیابی هم بذارید دیگه محشره?
سلام ممنون از انرژیتون.
حتما در دست بررسی است.
سلام من دانشجوی ترم اول مدیریت صنعتی هستم با پایه ریاضی بسیار ضعیف و دیپلم نظام قدیم ، نیاز من یاد گرفتند مشتق و انتگرال هست در حالیکه از توابع و معادلات اطلاعی ندارم ، از کجا باید شروع کنم و چطور ،،، متشکرم
با سلام و احترام
توصیه میکنم با یک معلم خصوصی این مطالب رو یاد بگیرید تا زودتر به نتیجه برسید
بختیاری
چجوری فهمیدی خداوکیلی من احساس شل مغزی
دارم اصلا ساده نیس یا اگه هس واسه من نیس
کمک فردا امتحان ترم حضوری دارم
با سلام وادب
دوست عزیز شما هم با دقت واین فکر که تو هم میفهمی بخون حتما متوجه میشی
خیییلی بده اصلا ریاضی مغز بدون دغدغه و فکر میخاد که باید درون جنگل ها این آدما رو پیدا کنیم??
ریاضی محشره
چون ذهن ادمو به چالش میکشه و هیچ جاش حفظی نیست لازم به تحلیلی داره?
منم امتحان دارم
آهههه منمم ریاضی دارم
معلم اومده فقط درس داده توضیح نداده
اگرم داده من یادم نیست
عالی ??? ای کاش آزمون آنلاین هم بذارید ??
سلام دوست عزیز
ممنون از پیام پر مهرتون
حتما در آینده قرار می دهیم.
موفق باشید
4aبلاوه ۵bبلاوه ۶aبلاوه bمساوی
با سلام وعرض ادب
دوست عزیز جملاتی که متغیرهاشون مثل هم هست با هم متشابهند ضرایبشون رو با هم جمع میکنیم پس میشود۱۰a بعلاوه ۷b
این چی میشه
-7+3x=_34
سلام واحترام
دوست عزیزاین یک معادله ساده هست کافیه هفت رو ببرید طرف دوم علامتش عوض میشه ومیشه بیست وهفت بعد به ضریب ایکس تقسیم کنید یعنی سه جواب میشه نه
سلام خوبی جواب معادله ۳x=16 چی می شود.
با سلام
خوبم کوچولو میشه شانزده سوم
ولی میشه10a+6b
خیلی عالی بود امیدوارم امتحان های آنلاین هم بزارید و من که واقعا لذت بردم و کاملا متوجه شدم
سلام و عرض ادب
ممنون از توجهی که داشتید. حتما در آینده داخل سایت قرار می دهیم.
موفق باشید.
سلام ممنون از توضیحاتتون
اما مثلا اگه چند تا منفی و چند تا مثبت داشتیم باید چطوری حساب کنیم
۳a+5b-4a+6
با سلام
جمله های متشابه را با هم جمع کنید
سلام…خيييلى خوب و كامل توضيح داديد??…اگه ميشه معادله هم بگيد????..فايتينگ?✨?
سلام و عرض ادب
ممنون از انرژیتون
معادله ریاضی هفتم هم میتوانید از لینک زیر دریافت کنید:
ٰhttps://riazica.com/equation/
موفق باشید
واقعا توضیحات عالی بودن خیلی ممنون ?????
با سلام واحترام
ممنون از شما دوست عزیز
معادله بایک مثال توضیح دهید
با سلام
معادله یه عبارت جبری هست که طرف دوم داره و حل معادله یعنی پیدا کردن مجهول
سلام خیلی مفید و اموزنده بود ممنون از شما.
با سلام واحترام
ممنون از شما وبذل توجهتون
با سلام :))
ممنون از بابت این صفحه خیلی خوب بود فقط من جملات رو متوجه نشدم، هیچ جای دیگه هم نتونستم بخونم و متوجه بشم کاش تعریفی ازش بجای مثال میزاشتید
مثلا میگفتید هر عدد و هر متغیر یک جمله هست مگه اینکه بین عدد یا متغیری ضرب باشه و اونو ساده کنیم، یا شاید بین دوتا عدد ضرب باشه هم ساده بشه جعتش بشن یه جمله نمیدونم…?
با سلام وعرض احترام
این پست رو مطالعه کنیدhttps://riazica.com/algebraic-expression-9/
عالی بود
با سلام
ممنون از لطف شما
اوخی عالی بود
با سلام وادب
ممنون دوست عزیز
متشابه ی جملهی ×۳ چیع
با سلام
هر یک جمله ای شامل ایکس با توان یک با این جمله متشابه هست
سلام ممنون از توضیحات
ببخشید می خواستم بدونم حاصل
7xyz.7xyz
چند جمله داره
با سلام وادب
حاصلضرب دو تا یک جمله ای میشه یک جمله ای
بسیار عالی و مختصر توضیح داده شده اگر در مورد بخش چهارم معادله هم بزارید سپاسگزاریم
با سلام وادب
ما تمام درسهای پایه هفتم رو گذاشتیم
سلام عالی توضیح داده بودید ??
با سلام و ادب
ممنون از نظر لطف شما
سلام خسته نباشید فقط میخاستم لون مسئله ۶ چطوری میشه من متوجه نشدم
با سلام واحترام
در مثال ۶ ابتدا علامت قرینه پشت پرانتز روی عبارت داخل پرانتز اثر میکنه و اونها رو قرینه میکنه وبعد عبارتهای متشابه رو ساده میکنیم
ببخشید جواب ۴a+۵b-۲a+b چی میشه؟
با سلام
دوست عزیز جملات متشابه رو با هم جمع کن پست روخوببخون به جوابت میرسی
سلام ممنون از توضیحات شما . یک سوال !
اگر علامت های داخل پرانتز با هم متشابه باشند مثل 2bو 4b و بیرون پرانتز هم یک عدد وجود داشته باشه باید اون عدد رو به هر دوی آنها ضرب کنیم یا داخل پرانتز را به دست بیاوریم و حاصل را ضرب در عدد بیرون پرانتز بکنیم؟؟؟
با سلام واحترام
دوست عزیز بهتر هست اول حاصل داخل پرانتز رو بدست بیاریم وبعد عدد پشت پرانتز رو در اون ضرب کنیم البته اگه اول ضرب کنیم بعد جمع هم مشکلی پیش نمیاد و جواب درسته
?عالی بود?
با سلام وادب
خواهش میکنم
۲a+۴b
با سلام
ممنون از پاسخگویی شما
سلام اما کی میتونه یه با توضیح با نوشته نه بلکه با حل کردن ❔
سلام مطالب بسیار عالی بود
توضیح هاتون در مورد عبارت جبر خیلی آموزنده بود بازم ازاین مطالب ها بزارین ممنون میشوم☺️
با سلام وادب
ممنون از شما ودیدگاهتون چشم حتما میذاریم
جواب a×a×a×aچی میشه ی توضیح ریز بده
با سلام
a پنج بار ضرب شده پس میشه aبه توان ۵
بااین که از ریاضی متنفرم ولی خوب توضیح داده بودید??تشکر?
با سلام
امیدوارم سایت ما شما رو عاشق ریاضی کنه
سلام خیلی عالی بود
سلام عرض خسته نباشید
مطالبتون خیلی مفید بود ممنون
جواب این چی میشه؟
4X_6Y+(_3X+2Y+7
سلام دوست عزیز
ممنون از نظر لطف شما در این سوال xها با هم وyها با هم متشابهند با توجه به علامتشان می شود x-4y+7
سلام
۷برابر عدد منهای یک برابر است با دوبرابر قرینه ی
همان عدد مورد نظر را پیدا کنید توی این موندم ?
مساحت مستطیل ،مربع،دایره و مثلث زیر را به صورت معادلاتی برحسب( ایکس )نوشته وسپس(ایکس)پیدا کنید
مساحت هر۴شکل برابر ۶۴سانتی متر مربع میباشد
داخل دایره یه خط به همراه ایکس هست
توی مثلث همین طور این دفعه یه ایسک و ایکس ۲ هست
مربع یه ایسک داره
مستطیل یه ۸ایکس و یه ۴ ایکس داره
میشه کمکم کنید ????????????
ممنون میشم اگه کمکم کنید ??????
سلام دوست عزیز برا سوال اول اگه معادله بنویسی وحل کنی جواب میشه یک نهم ولی سوال دوم رو متوجه نشدم ولی اونم از راه معادله حل میشه
سلام من فردا امتحان ریاضی دارم از فصل ۳ ریاضی هفتم خیلی استرس دارم خوب بلد هم نیستم چون هر دفعه امتحان ریاضی ام رو ۲۰ دادم ولی از این دفعه مطمئن نیستم
سلام دوست عزیز
بدون استرس وبا توکل به خدا امتحان بده نمره ملاک نیست یادگیری مفاهیم مهمه
مگه وسط این عدد که منفی هست مثبت نمیشه بعد عدد دیگه قرینه اش بشه
3x+5)-(2x-4))
بشه این?
3x+5)(2x+4))
یا اشتباهه
با سلام دوست عزیز
اشتباهه باید منفی رو تاثیر بدید وبعد کل پرانتزها رو بردارید
خیلی عالی و کامل بود
اسون بود
كمون از توضيحات جامع تون
با سلام خدا رو شکر مفید بوده برای شما
عالی
عالی
سلام خسته نباشید با این چیز هایی داخل سایت گذاشتین من خیلی خوب یاد گرفتم
فقط ای کاشکی معادله روهم توضیح میدادین اگه میشه داخل سایت تون بزارین ممنون میشم چون تو معادله و حل مسئله خیلی ضعیفم
سلام دوست عزیز
برای معادله هم درسنامه هم ویدیو گذاشتیم