آموزش ریاضی پایه هشتم
جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
خرداد
آیا اگر ماشین حساب نداشته باشید، می‌توانید جذر یک عدد را محاسبه کنید؟ در ریاضیات با اعداد رادیکالی زیاد مواجه میشویم. برای محاسبه جذر چند راه وجود دارد. ما دراین مطلب جذر تقریبی را با استفاده از دو عدد طبیعی متوالی قبل و بعد آن عدد رادیکالی یاد خواهیم گرفت.
در درسنامه جذر تقریبی هشتم از مجموعه آموزش ریاضی پایه هشتم در ابتدا یادآوری کوتاهی از مفهوم جذر و همچنین روش محاسبه جذر به کمک ماشین‌حساب ذکر میشود. سپس به آموزش روش جذر تقریبی عدد تا یک، دو و چند رقم اعشار می‌پردازیم.
یادآوری مفهوم جذر
در درسنامه جذر وریشه ریاضی هفتم مفهوم جذر یک عدد (یا ریشه دوم یک عدد) را یاد گرفتیم. به زبان ساده: مفهوم جذر، برعکس مفهوم به توان 2 رساندن (مربع کردن یک عدد) است.
به این تساوی دقت کنید: \(\Large (-6)^2=36 , (6)^2=36 \). به اعداد 6 و 6- ریشه‌های دوم 36 می‌گویند. همچنین به عدد 36، مجذور 6 و 6- گفته میشود. به نکات زیر توجه کنید:
- هر عدد مثبت بجز 1، دو ریشه دوم دارد که یکی، قرینه دیگری است.
- در جذرگیری، تنها عدد مثبت در نظر گرفته میشود. جذر با علامت (\(\Large \sqrt {\text{ }} \)) نشان داده میشود.
بنابراین جذر عدد 100 برابر است با 10 ( \(\Large \sqrt{\mathstrut 100}=10 \) )
- اعداد منفی، جذر ندارند؛ چون مجذور هیچ عددی منفی نمی‌شود. (گشتم نبود، نگرد نیست!)
- جذر اعداد 0 و 1 برابر با خود آن اعداد هستند..( \(\Large \sqrt{\mathstrut 1}=1 \) )و( \(\Large \sqrt{\mathstrut 0}=0 \) )
محاسبه جذر به کمک ماشین‌حساب
برای محاسبه جذر یک عدد با استفاده از ماشین‌حساب، مطابق شکل باید گزینه (\(\Large \sqrt {\text{ }} \)) را بزنیم:
- ماشین‌حساب معمولی: ابتدا نوشتن عدد و سپس زدن (\(\Large \sqrt {\text{ }} \))
- ماشین‌حساب مهندسی: ابتدا زدن (\(\Large \sqrt {\text{ }} \)) و سپس نوشتن عدد
در هر نوع ماشین‌حساب، تعداد رقم‌های محدودی برای نمایش وجود دارد؛ برای محاسبه جذر تقریبی با ماشین حساب، تعداد رقم اعشاری خواسته شده را جدا کرده و رقم آخر را گرد میکنیم ؛ یعنی با توجه به عدد سمت راست آخرین رقم، در صورتی که آن عدد ۵ یا بزرگتر از ۵ باشد ،یک واحد به آن اضافه شده و در صورتی که کمتر از ۵ باشد آن رقم ثابت می‌ماند (یادآوری: ریاضی ششم دبستان).
مثال 1: جذر تقریبی عدد 34 را با استفاده از ماشین حساب تا 4 رقم اعشار بدست آورید.
حل 1:
ابتدا روی ماشین حساب ساده زیر، عدد 34 را نوشته و سپس علامت (\(\Large \sqrt {\text{ }} \)) را می‌زنیم؛ مشاهده میشود که مقدار جذر تقریبی را تا 7 رقم اعشار محاسبه کرده است.
مطابق صورت سؤال، 4 رقم اعشار خواسته شده است. بنابراین 5/9160 را جدا کرده و برای گرد کردن، با توجه به این که رقم سمت راست آن، یعنی رقم 7 بزرگتر از 5 است، یک واحد به رقم آخر اضافه میکنیم: 5/9161.
روش بدست آوردن جذر تقریبی یک عدد
با محاسبه جذر در ریاضیات پایه‌های مختلف سر و کار داریم، اما روش جذر تقریبی هشتم از دو عدد صحیح قبل و بعد از عدد مورد نظر کمک می‌گیرد.
جذر تقریبی تا یک رقم اعشار
فرض کنید می‌خواهیم جذر تقریبی عدد 56 را بدست آوریم. برای این کار ابتدا مجذورهای کامل قبل و بعد آن را مشخص میکنیم. 56 بین اعداد 49 و 64 قرار گرفته. پس\(\Large \sqrt {56} \) نیز بین جذر این دو عدد قرار خواهد داشت:
\(\Large 49 < 56 < 64 \)
\(\Large → \sqrt {49} < \sqrt {56} < \sqrt {64} \)
\(\Large → 7 < \sqrt {56} < 8 \)
نکته: مجذور کامل، عددی است که از به توان 2 رساندن (مربع کردن) یک عدد صحیح بدست آمده است. مانند اعداد 1، 4، 9، 16 و … (که به ترتیب برابر با \(\Large 1^2 \)، \(\Large 2^2 \)، \(\Large 3^2 \)، \(\Large 4^2 \) و … هستند).
خب ادامه مطلب: سپس عدد وسط این دو عدد (یعنی \(\Large 7/5 \)) را مجذور میکنیم. اگر بزرگتر از 56 بود، باید اعداد کوچکتر از 7/5 و اگر کوچکتر بود، باید اعداد بزرگتر از 7/5 را بررسی کنیم.
\(\Large 7/5^2= 56/25 \)
چون 56/25 بزرگتر از 56 است، اعداد کمتر از آن با یک رقم اعشار را در جدولی مانند جدول زیر نوشته و مجذور هر یک را حساب میکنیم تا نزدیک‌ترین عدد به 56 را پیدا کنیم.
| 7/4 | 7/3 | 7/2 | 7/1 | عدد |
|---|---|---|---|---|
| 54/76 | 53/29 | 51/84 | 50/41 | مجذور |
- مجذور کدوم عدد به 56 نزدیکتره؟ مجذور 7/4 ؟ یه کم بیشتر دقت کن! درسته توی جدول این عدد نزدیک‌ترینه، ولی اگه با مجذور 7/5 مقایسه کنی، می‌بینی که 56/25 نزدیکتر از 54/76 به عدد مورد نظر ماست.
پس جذر تقریبی 56 تا یک رقم اعشار برابر با 7/5 است.
جذر تقریبی با تعداد رقم‌های اعشاری بیشتر
اگر بخواهیم در مثال قبل بخواهیم \(\Large \sqrt {56} \) را تا دو رقم اعشار بدست آوریم، این بار همان مراحل را با اعداد 7/4 و 7/5 انجام می‌دهیم (چون 56 بین مجذور این دو عدد قرار داشت):
عدد وسط 7/4 و 7/5 (یعنی 7/45) را به توان 2 میرسانیم و باز هم با 56 مقایسه میکنیم. اگر بزرگتر از 56 بود، اعداد کوچکتر از 7/45 و اگر کوچکتر بود، اعداد بزرگتر از 7/45 را در جدول می‌نویسیم.
\(\Large 7/45^2= 55/50 \)
مجذور 7/45 کوچکتر از 56 است، پس اعداد بزرگتر از 7/45 را در جدول نوشته و مجذور هر یک را محاسبه میکنیم:
| 7/49 | 7/48 | 7/47 | 7/46 | عدد |
|---|---|---|---|---|
| 56/10 | 55/95 | 55/80 | 55/65 | مجذور |
- مجذور کدوم عدد به 56 نزدیکتره؟ مجذور 7/48؟ آفرین! درسته.
پس جذر تقریبی 56 تا دو رقم اعشار برابر با 7/48 است. برای ارقام اعشاری بیشتر از 2 نیز همین مراحل را تکرار میکنیم.
خلاصه مراحل محاسبه جذر تقریبی
برای بدست آوردن جذر تقریبی یک عدد، به ترتیب مراحل زیر را انجام می‌دهیم:
- مشخص میکنیم که عدد مورد نظر بین کدام دو عدد صحیح متوالی است.
- عدد وسط آن دو عدد صحیح را مشخص کرده و مجذور آن را حساب میکنیم.
- اگر مجذور عدد وسط، بزرگتر از عددی است که می‌خواهیم جذر آن را محاسبه کنیم، 4 عدد کمتر و اگر کوچکتر است، 4 عدد بیشتر از عدد وسط را در جدول می‌نویسیم.
- مجذور هر یک از این 4 عدد را بدست می‌آوریم و با عدد مورد نظر مقایسه میکنیم.
- جذر تقریبی (تا یک رقم اعشار) برابر با عددی است که مجذورش به عدد مورد نظر نزدیکتر باشد.
- برای محاسبه جذر تا دو رقم اعشار، مراحل 1 تا 5 را برای اعداد با یک رقم اعشار انجام می‌دهیم و برای ارقام اعشاری بالاتر باز هم ادامه می‌دهیم.
مقایسه اعداد با استفاده از جذر تقریبی
به کمک روش جذر تقریبی هشتم می‌توانیم اعداد رادیکالی را با هم مقایسه کرده و یا محل تقریبی آن را روی محور نشان دهیم (البته روش دقیق نمایش عدد رادیکالی بر روی محور در درسنامه نمایش عدد رادیکالی روی محور توضیح داده شده است).
برای این کار کافی است مراحل محاسبه جذر تقریبی را انجام داده و مشخص کنیم که جذر عدد بین کدام دو عدد قرار دارد. به عنوان نمونه، از مرحله بالا (جدول) میدانیم که \(\Large \sqrt {56} \) بین 7/48 و 7/49 قرار دارد. پس محل تقریبی آن بر روی محور اعداد نیز به این صورت خواهد بود:
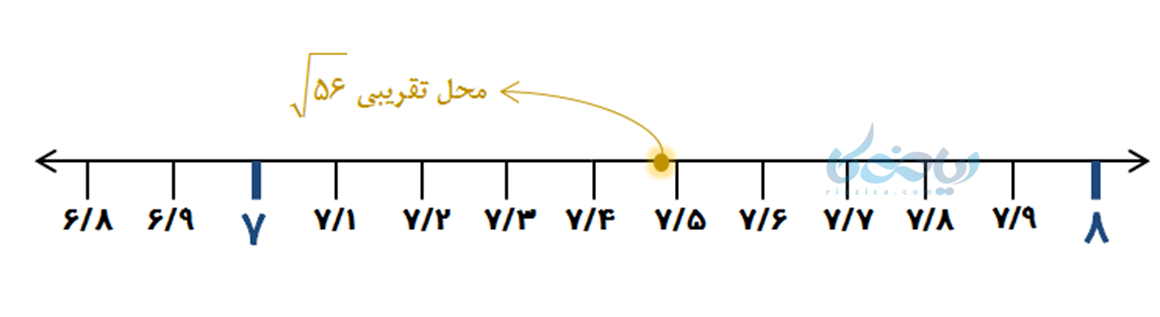
مثالی از کاربرد جذر تقریبی برای مقایسه اعداد
مثال 2: در عبارت زیر علامت مناسب قرار دهید و روی محور اعداد نیز بصورت تقریبی این مقایسه را نشان دهید.
حل 2:
برای مقایسه این دو عدد می‌توانیم هر دو را به توان 2 رسانده و مقایسه کنیم. اما اگر بخواهیم از روش این درس یعنی جذر تقریبی هشتم پیش برویم، باید جذر تقریبی \(\Large \sqrt {18} \) را محاسبه کنیم:
\(\Large 16 < 18 < 25 \)
\(\Large → \sqrt {16} < \sqrt {18} < \sqrt {25} \)
\(\Large → 4 < \sqrt {18} < 5 \)
مجذور عدد وسط (4/5) برابر با 20/25 است و به دلیل آن که از 18 بزرگتر است، اعداد کوچکتر از 4/5 را در جدول می‌نویسیم:
| 4/4 | 4/3 | 4/2 | 4/1 | عدد |
|---|---|---|---|---|
| 19/36 | 18/49 | 17/64 | 16/81 | مجذور |
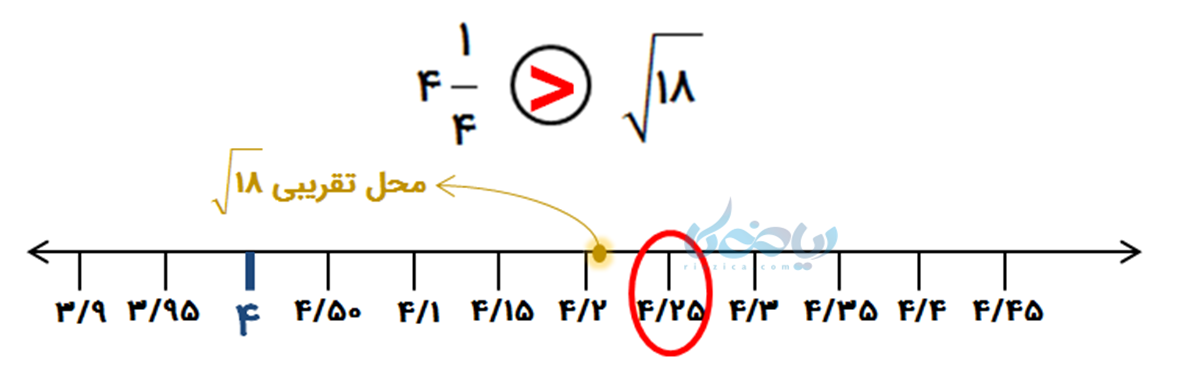
فاصله 17/64 و 18/49 تا عدد 18 به ترتیب برابر با 0/34 و 0/51 است؛ پس جذر تقریبی \(\Large \sqrt {18} \) برابر است با 4/2. پس از عدد مخلوط (برابر با 4/25) کمتر است.
همچنین می‌توان با نمایش تقریبی \(\Large \sqrt {18} \) بر روی نمودار، آن را با 4/25 مقایسه نمود (توجه کنید که بیشتر از 4/2 است؛ چرا؟؟ چون مجذور آن، یعنی 18 بزرگتر از مجذور 4/2 یعنی 17/64 است).
قسمتی از فایل ویدیویی جذر تقریبی ریاضی هشتم
برای خرید فایل کامل این ویدیو دکمه خرید زیر این ویدیو را کلیک کنید.
توصیه می شود قبل از خواندن این پست درسنامه جذر وریشه ریاضی هفتم را بخوانید.
زنگ آخر کلاس جذر تقریبی هشتم
در آموزش جذر تقریبی هشتم با یادآوری مفهوم جذر یا ریشه دوم و روش استفاده از ماشین‌حساب کلیات بحث را یاد گرفتیم و سپس روشی مفید و البته سریع برای محاسبه جذر تقریبی یک عدد را به کار بردیم. با این روش توانستیم عددهای رادیکالی را با دیگر اعداد مقایسه کنیم و همچنین محل تقریبی آن را بر روی محور اعداد نمایش دهیم؛ البته در درسنامه نمایش عدد رادیکالی روی محور روش نمایش دقیق عدد رادیکالی بر روی محور آموزش داده شده است. البته در پایه‌های بالاتر باز هم با ریشه‌گیری سر و کار خواهیم داشت.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی هشتم به شما پیشنهاد می‌دهیم:
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- زاویه های خارجی 🏰🔶 – نگهبان قلعه چندضلعیها!
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📍 – مبحثی کاربردی در هندسه!
- همه چیز درباره جدول فراوانی 📊📝 ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 💰🎲 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 👣✅ – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️🔛 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یکضرب یاد بگیر!
- شکل های هم نهشت آموزش ریاضی هشتم 🔷🔶 – کپی برابر اصل!
- رابطه فیثاغورس ریاضی هشتم 🎮📐 – وزیر بازی مثلثات!
- مثلث های هم نهشت 🌷🔺 گل سرسبد شکلهای همنهشت!
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعیها!
- تعریف اعداد گویا و … ! ➗🔡 همه چیز اینجاست!
- بردارهای واحد مختصات 👣➡️ – قدم قدم بشمار!
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- عدد اول ریاضی هشتم 1️⃣👨🎓 – کاملترین آموزشی که لازم داشتید.
- بردار و مختصات ریاضی هشتم ➡️⬅️ – جهتدار و کامل!
- فاکتورگیری ریاضی هشتم 🔡➕➖ – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🍩📝 – سرآغاز یک بحث شیرین ریاضی!
- چهار ضلعی ها ✏️🔶 – آشنایی با یک خانواده جذاب!
- خطوط موازی و مورب #️⃣🚘 ؛ رانندگی خطها در چهارراه زاویه!
- اعداد صحیح ↔️➖➕– نمایش روی محور مختصات
- ساده کردن عبارت های جبری 📣🎓 ؛ مختصر و مفید با صدای بلند!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!
- خط و دایره : از سیر ➖ تا پیاز 🔴
چیکار کنم هیچی بلد نمیشم
با سلام وعرض ادب
شروع کن بخون از اول کتاب ما هم کمکت می کنیم
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
جذر ۳۴ تا یک رقم اعشار
با سلام وعرض ادب
عزیزم پست رو مطالعه کنید و خودتون محاسبه کنید
ببخشید جذر ۳۷۰ چی میشه؟
گفتم عدد 34 تا دو رقم اعشار
با سلام
کی گفتید؟ ۳۴ بین ۲۵ و۳۶ هست پس جذرش بین ۵وشش چون به ۳۶ نزدیکتره اعشار نزدیک ۶ رو امتحان میکنیم ومیشه 5/83
ای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام . ممنون از سایتتون. من جذر تا دو رقم اعشار رو اصلا بلد نبودم با کمک سایتتون بهتر یاد گرفتم . ممنون از شما
با سلام وعرض ادب
خوشحالیم که براتون مفید بوده معرف ما به دوستانتون باشید
جذر ۸۷ چی میشه با چهار مرحله اش میخوام
با سلام وعرض ادب
منظورتون از چهار مرحله چی هست؟
سلام چجوری بدونیم که عدد مورد نظرمون بین چه اعدادیه
مثلا ؟ ۲۷ ؟
سلام و عرض ادب
کافیه اعداد مجذور کامل را بشناسید تا بدانید عدد موردنظر بین چه مجذورهای کاملی قرار دارد.
۲۷ بین ۲۵ و ۳۶ قرار دارد. پس جذرش بین ۵ و ۶ می باشد.
سلام ببخشید سوال:جذرتقریبی عدد۹۷۰راتایک رقم اعشارباراه حل حل کنید
با سلام و عرض ادب
۹۷۰ بین ۹۶۱ و ۱۰۲۴ است پس جذرش بین ۳۱ و ۳۲ می باشد.
سلام من جذر تقریبی رادیکال۵۰رو میخام
با سلام وعرض ادب
به همون روشی که در پست گفتیم عمل کنید
سلام جذر تقریبی رادیکال ۱۹ چیه اگه بشه بگید
با سلام وعرض ادب
۴/۳میشه
سلام
فکر کنم
4.3*4.3=18.49
4.4*4.4=19.36
19 به 19.36 نزدیکتره پس جذر 19 باید بشه 4.4
با سلام وعرض ادب
دوست عزیز جذر ۱۸ خواسته شده نه نوزده در مثال مورد نظر شما
سلام جواب این سوال چی میشه
جذر هر عدد کوچک تر از واحد از خودش.………است
با سلام
بزرگتر است
باسلام ببخشید من جذرتقریبی رادیکال۲۸ رو میخوام
سلامدوست عزیز روش رو گفتیم خودتون بدست بیارید
ببخشید میشه یک راه حل بدهید تا بتوانیم ریاضی و فرمول های آن را بهتر یلد بگیریم
با سلام واحترام
فقط سعی کنید ریاضی رو مفهومی یاد بگیرید وبعدبا تمرین وتکرار همه چی درست میشه
سلام ببخشید ما اگه بخواهیم جذر یک عدد اعشاری مثل ۰.۶ را بدست اوریم باید چکار کنیم؟
سلام ببخشید برای اینکه جذر تقریبی عدد ۰.۶ را بدست بیارم باید چیکار کنم ؟؟
یا اگه جذر تقریبی یک عدد اعشاری با دو رقم اعشار مثل ۰.۶۸ امد برای جواب باید چیکار کنم؟؟
با سلام وعرض ادب
مثل بقیه اعداد فقط اینها بین صفر ویک هستن وجدرشان از خودشان بزرگتر است مثلا برای ۰/۶ جز صحیحش صفر میشود میدانیم ۰/۵ به توان دو میشود ۰/۲۵ پس اعاد بزرگتر از ۰/۵ را بتوان دو میرسانیم وتوجه میشویم ۰/۸ به این عدد نزدیکتر است البته بخواهیم تا دو رقم اعشار حساب کنیم ۰/۷ را درنظر میگیریم ودوباره ۰/۷۵ را به توان دو میرسانیم تا به واب برسیم
جذر عدد 14تا یک رقم اعشار بدست بیار(نوشتن فرمول الزامی است)
جذر ۹۴ را تا یک رقم اعشاری بدست آورید ممنون میشم اگه الان جواب بدین
جذر تقریبی رادیکال۱۹ با راه حل لطفا
با سلام وعرض ادب
پست رو بخونید خودتون پیدا کنید
سلام جذر تقریبی عدد 54 را به دست اورید
سلام مطالب بسیار مفید و خوب بود ممنون فقط اینکه روش حذر تقریبی با جدول کلا درباره این موضوع اگر کسی مطلبی داره میشه بگید؟چون کنفرانس دارم یکم مطلب کم آوردم ممنون
سلام جواب این سوال چی میشه
جذر هر عدد کوچکتر از واحد از خودش………است
سلام عالی بود
فقط یه سوال داشتم روش دیگه ای برای پیدا کردن جذر وجود داره؟
سلام دوست عزیز
بله هست
سلام ممنون مطالب مفید بود.
میشه لطفا بگین 93/√ این رو چجوری باید حل کرد
سلام
میشه جذر تقریبی رادیکال ۱۷رو تا یک رقم اعشار با راه حل و جزئیات محاسبه کنید
سلام دوست عزیز پست رو بخوانید وبا لذت خودتون به دست آورید.
سلام ببخشید میشه جذرتقریبی ۳۰ روهم توضیح بدید ممنون میشم
سلام دوست عزیز پست رو بخوانید و خودتون به دست آورید.
بد نبود ولی بعضی توضیحات غلطه
با سلام وادب
میشه دقیقا بگید کجا غلطه تا اصلاح بشه
خیلیییی ممنوووون
خواهش میکنم دوست عزیز
سلام ممنون♥️
اما جذر تقریبی ۵۶ نمیشه ۷/۵ چون ۵۶/۲۵ هنوز ۰/۲۵ بیشتر داره پس باید بیایم عقب که یعنی ۷/۴ میشه (۵۴/۷۶)
معلم ما بهمون اینجوری گفته ینی کمتر میتونه باشه ولی بیشتر نه
ممنونم