آموزش ریاضی پایه دوازدهم تجربی
مقاطع مخروطی و بیضی 💎🏉 ریاضی دوازدهم تجربی – به راحتی آب خوردن! ?
در این درسنامه، با مقاطع مخروطی آشنا میشویم. سطح مخروطی را معرفی میکنیم و بعد از آشنایی با هذلولی، به طور مفصل به بیضی میپردازیم. از آنجاییکه برای معرفی مقاطع مخروطی به دوران و برش نیاز داریم، ابتدا در مورد این دو موضوع بحث خواهیم کرد.
دوران
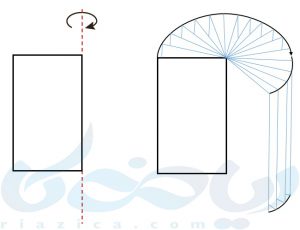
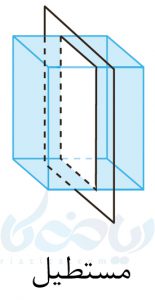
با دوران هر شکل حول یک خط (محور)، شکلی جدید حاصل خواهد شد. مثلاً اگر مانند شکل زیر، یک مستطیل را حول یک خط دوران دهیم، یک استوانه به دست میآید.
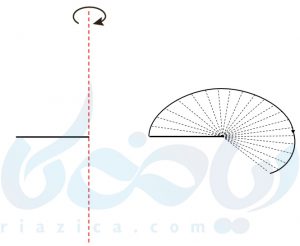
در صورتی که یک پارهخط را حول خطی که بر آن عمود است دوران دهیم، یک دایره ایجاد خواهدشد. به شکل زیر دقت کنید:
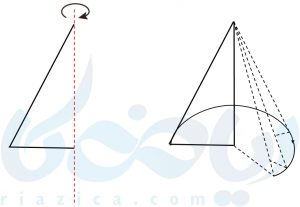
اگر مانند شکل زیر، یک مثلث قائم الزاویه را حول یکی از اضلاع قائمهی آن دوران دهیم، شکل حاصل مخروط خواهد بود.
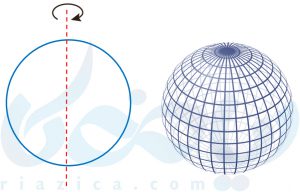
از دوران یک دایره حول یکی از قطرهای آن، یک کره به وجود میآید. به شکل زیر دقت کنید:
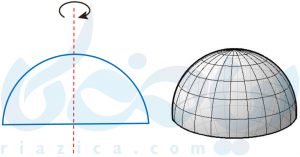
همانطور که در شکل زیر مشخص است، شکل حاصل از دوران یک نیمدایره حول شعاع عمود بر قطر آن، یک نیمکره خواهدبود.
برش
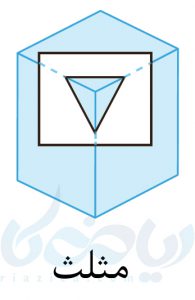
اصطلاحا به برخورد یک صفحه با یک شکل هندسی، برش آن شکل گفته و به شکل حاصل از این برش، سطح مقطع میگویند. برش، کابرد کلیدی در تعریف مقاطع مخروطی دارد. برای اینکه بهتر متوجه شوید، به شکلهای زیر نگاه کنید. در هر کدام از این شکلها، یک صفحه با یک مکعب مستطیل برخورد کرده است. سطح مقطع حاصل از هر کدام در زیر شکل نوشته شده است.
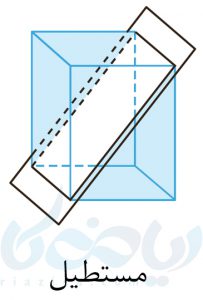
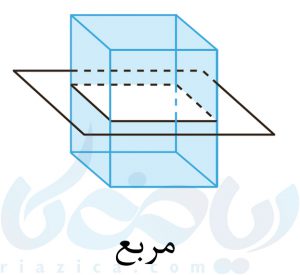
در شکلهای زیر نیز میتوانید سطح مقطع استوانه با صفحههای عمودی، افقی و مایل را مشاهده کنید. باید توجه داشت، صفحهی مایل با قاعدهی استوانه، متقاطع نیست. در غیر این صورت، شکل دیگری حاصل میشد.



مثال 1: سطح مقطع حاصل از برخورد یک صفحه با یک کره چیست؟
حل: همانطور که در شکل زیر مشاهده میکنید، سطح مقطع حاصل از برخورد یک صفحه با یک کره، دایره است. این سطح مقطع زمانی بیشترین مساحت را دارد که مرکز کره روی آن قرار داشته باشد.

مقاطع مخروطی
شکل زیر را در نظر بگیرید. دو خط \( \Large d \) و \( \Large l\) متقاطعاند. اگر خط \( \Large d\) را حول خط \( \Large l\) دوران دهیم، شکلی به وجود خواهدآمد که به آن سطح مخروطی میگوییم. به خط \( \Large l \) محور، به نقطهی \( \Large O \) راس و به خط \( \Large d \) مولد این سطح مخروطی گفته میشود.
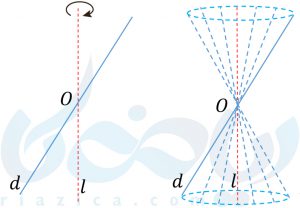
اگر یک سطح مخروطی را با یک صفحه برش دهیم، مقطع مخروطی به وجود میآید. با توجه به موقعیت صفحه و سطح مخروطی، مقاطع مخروطی متفاوتی حاصل خواهدشد. در ادامه به بررسی هر یک از این مقاطع خواهیم پرداخت.
دایره، اولین شکل در بررسی مقاطع مخروطی
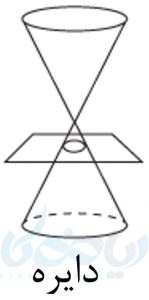
به شکل زیر نگاه کنید. اگر سطح مخروطی را با یک صفحه که بر محور سطح مخروطی عمود است و از مرکز آن عبور نمیکند برش دهیم، سطح مقطع، دایره خواهد بود.
سهمی
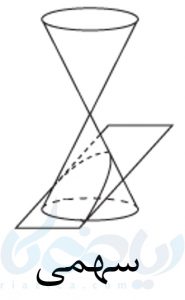
اگر سطح مخروطی را با صفحهای برش دهیم که با مولد سطح مخروطی موازی است و از راس آن عبور نمیکند، شکل حاصل سهمی خواهدبود. به شکل زیر نگاه کنید:
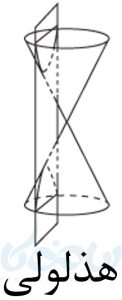
هذلولی
در صورتی که سطح مخروطی را با صفحهای برش دهیم که هم قسمت بالایی و هم قسمت پایینی سطح مخروطی را قطع کند و از راس آن عبور نکند، سطح مقطع حاصل، یک هذلولی خواهد بود. به شکل زیر دقت کنید:
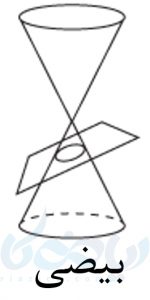
یک شکل مهم در مقاطع مخروطی : بیضی
اگر سطح مخروطی را با صفحهای برش دهیم که نه بر محور سطح مخروطی عمود باشد، نه با مولد سطح مخروطی موازی شود و نه از راس سطح مخروطی عبور کند، سطح مقطع حاصل، بیضی خواهدبود. به شکل زیر نگاه کنید:
بیضی، بررسی بیشتر
دو میخ و یک تکه نخ به طول \( \Large d \) را در نظر بگیرید. دو سر نخ را به وسیلهی دو میخ ثابت میکنیم. اگر مانند شکل زیر، مداد را در حالتی که نخ کشیده شده، روی صفحه حرکت دهیم، بیضی رسم خواهد شد. در هر نقطه از بیضی، مجموع فاصله از دو میخ برابر است با طول نخ. پس در هر نقطه مجموع فاصله از دو میخ، عدد ثابتی است. در نتیجه، بیضی مجموعهی نقاطی از صفحه است که جمع فواصل آن نقاط از دو نقطهی ثابت در صفحه، عددی ثابت است.برای اطلاعات بیشتر رسم بیضی را مشاهده کنید
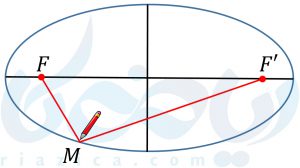
به دو نقطهی ثابتی که در رسم، همان میخ ها بودند و در شکل بالا نیز با حروف \( \Large F\) و \( \Large F’\) مشخص شدهاند، کانونهای بیضی میگوییم. اگر نقطهای خارج از بیضی باشد، مجموع فواصل آن از دو کانون بیضی، بیشتر از \( \Large d \) و اگر درون بیضی باشد، مجموع فواصل آن از دو کانون، بیشتر از \( \Large d \) خواهد بود. به شکل زیر نگاه کنید:
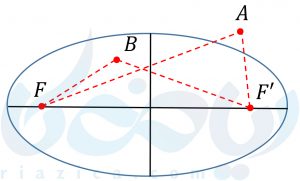
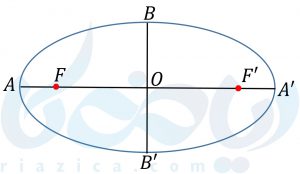
بیضی زیر را در نظر بگیرید. اندازهی \( \Large FF’ \) را فاصلهی کانونی بیضی و نقطهی میانی پاره خط \( \Large FF’ \) را مرکز بیضی مینامیم. پاره خط \( \Large AA’ \) که از دو کانون عبور میکند، قطر بزرگ بیضی است. پاره خط \( \Large BB’ \) که از مرکز عبور میکند و بر قطر بزرگ عمود است، قطر کوچک است. اگر قطر بزرگ، افقی باشد، بیضی افقی است. اگر قطر بزرگ، عمودی باشد، بیضی قائم است.

روابط مهم در بیضی
در این قسمت دو رابطهی مهم برای بیضی که یکی از مقاطع مخروطی ویژه است، به دست خواهیمآورد. رابطهی اول مربوط به قطر بزرگ بیضی است و رابطهی دوم در ارتباط با قطر بزرگ، قطر کوچک و فاصلهی کانونی بیضی است.
رابطهی قطر بزرگ بیضی با مقدار ثابت
بیضیهای زیر را در نظر بگیرید. اولین بیضی افقی و دومی قائم است. همانطور که میبینید، اندازهی نصف قطر بزرگ را با \( \Large a\)، اندازهی نصف قطر کوچک را با \( \Large b\) و اندازهی نصف فاصلهی کانونی را با \( \Large c\) مشخص کردهایم.
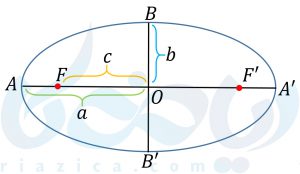


فرقی نمیکند که بیضی افقی را در نظر بگیرید یا بیضی قائم. نقطهی \( \Large A\) یکی از نقاط تشکیل دهندهی بیضی است. پس طبق تعریف بیضی، مجموع فواصل نقطهی \( \Large A\) از کانون ها برابر با مقدار ثابت است. در نتیجه داریم:
\( \LARGEمقدار ثابت= AF+AF’\)
\( \LARGE=AF+(AF+FF’)\)
\( \LARGE=2AF+FF’\)
نقطهی \( \Large A’\) نیز یکی از نقاط تشکیل دهندهی بیضی است. پس مجموع فواصل آن از کانونها برابر با مقدار ثابت است. در نتیجه داریم:
\( \Largeمقدار ثابت= A’F’+A’F\)
\( \Large=A’F’+(A’F’+FF’)\)
\( \Large=2A’F’+FF’\)
پس هم مقدار \( \Large 2AF+FF’\) و هم مقدار \( \Large 2A’F’+FF’\) برابر است با مقدار ثابت. در نتیجه:
\( \LARGE 2AF+FF’\)
\( \LARGE = 2A’F’+FF’\)
\( \LARGE \Rightarrow 2AF= 2A’F’\)
\( \LARGE \Rightarrow AF= A’F’\)
پس میتوانیم \( \Large AF\) را با \( \Large A’F’\) جایگزین کنیم. اگر مجموع فواصل \( \Large A\) از دو کانون را بازنویسی کنیم، خواهیمداشت:
\( \LARGEمقدار ثابت= AF+AF’\)
\( \LARGE=A’F’+AF’\)
\( \LARGE=AA’\)
در نتیجه میتوان گفت مجموع فواصل هر نقطه از بیضی از دو کانون، برابر با مقدار ثابتی است و این مقدار ثابت برابر است با اندازهی قطر بزرگ بیضی. این رابطه، یکی از مهم ترین روابط برای بیضی به عنوان یک مقطع مخروطی است.
رابطه بین اقطار و فاصلهی کانونی بیضی
با استفاده از رابطهی مهمی که برای قطر بزرگ بیضی در قسمت قبل به دست آوردیم، رابطهی دیگری استخراج خواهیمکرد. بیضی زیر را در نظر بگیرید.
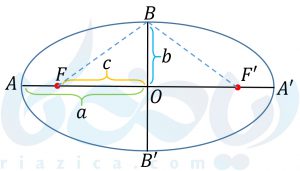
مجموع فواصل \( \Large B\) از دو کانون برابر است با مقدار ثابت. پس:
\( \LARGEمقدار ثابت= BF+BF’\)
قطر کوچک بیضی بر قطر بزرگ عمود است. از طرفی مرکز بیضی، وسط فاصلهی دو کانون قرار دارد. پس \( \Large B\) روی عمود منصف پارهخط \( \Large FF’\) است. در نتیجه \( \Large BF=BF’\). پس داریم:
\( \LARGEمقدار ثابت= BF+BF’\)
\( \LARGE=BF+BF\)
\( \LARGE=2BF\)
قضیهی فیثاغورث را در مثلث قائم الزاویهی \( \Large BFO\) مینویسیم:
\( \LARGE BF^2=BO^2+OF^2\)
\( \LARGE \Rightarrow BF^2=b^2+c^2\)
از طرفی \( \Large 2BF\) برابر است با مقدار ثابت و طبق رابطهی مهمی که به دست آوردیم، مقدار ثابت برابر است با طول قطر بزرگ، یعنی \( \Large 2a\). پس:
\( \LARGE 2BF=2a\)
\( \LARGE \Rightarrow BF=a\)
از آنجاییکه نشان دادیم \( \Large BF\) برابر با \( \Large a\) است و نشان دادیم \( \Large BF^2=b^2+c^2\)، خواهیمداشت:
\( \LARGE a^2=b^2+c^2\)
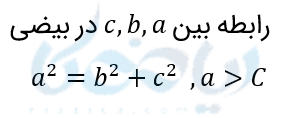
مثالهای مهم از روابط بیضی در مقاطع مخروطی
مثال 2: کانونهای یک بیضی نقاط \( \Large F=(5, 3)\) و \( \Large F’=(-3, 3)\) هستند. اندازهی قطر کوچک 6 است. اندازهی قطر بزرگ را پیدا کنید.
حل: فاصلهی کانونی که همان اندازهی \( \Large FF’\) است، برابر است با:
\( \Large \sqrt{(5+3)^2+(3-3)^2}=8\)
پس مقدار \( \Large c\) که نصف فاصلهی کانونی است، برابر است با 4. از طرفی اندازهی قطر کوچک 6 است. در نتیجه مقدار \( \Large b\) که نصف قطر کوچک است، 3 میشود. پس داریم:
\( \LARGE a^2=b^2+c^2\)
\( \LARGE \Rightarrow a^2=3^2+4^2\)
\( \LARGE \Rightarrow a=5\)
پس اندازهی قطر بزرگ که همان \( \Large 2a\) است، برابر است با 10.
مثال 3: فاصلهی کانونی یک بیضی برابر با 8 است. اگر مرکز بیضی نقطهی \( \Large O=(2, 3)\) باشد و نقطهی \( \Large B=(2, 6)\) یکی از نقاط بیضی باشد که روی قطر کوچک واقع است، مختصات نقاطی از بیضی که روی قطر بزرگ واقعاند را به دست آورید.
حل: فاصلهی کانونی 8 است. پس \( \Large c\) برابر است با نصف آن، یعنی 4. اندازهی \( \Large BO\) همان مقدار \( \Large b\) است، پس:
\( \begin{aligned}\LARGE b&\Large=\sqrt{(2-2)^2+(6-3)^2}\\&\LARGE=3\end{aligned}\)
\( \begin{aligned}\LARGE a^2&\LARGE=b^2+c^2\\&\LARGE=3^2+4^2\end{aligned}\)
\( \LARGE \Rightarrow a=5\)
با توجه به مختصات کانونهای بیضی، بیضی افقی است. در نتیجه برای به دست آوردن \( \Large A\) و \( \Large A’\) داریم:
\( \begin{aligned}\LARGE A&\LARGE=O-(5, 0)\\&\LARGE=(2, 3)-(5, 0)\\&\LARGE=(-3, 3)\end{aligned}\)
\( \begin{aligned}\LARGE A’&\LARGE=O+(5, 0)\\&\LARGE=(2, 3)+(5, 0)\\&\LARGE=(7, 3)\end{aligned}\)
خروج از مرکز بیضی
به مقدار \( \Large \frac{c}{a} \)، خروج از مرکز بیضی میگوییم و آن را با حرف \( \Large e\) نشان میدهیم. از آنجاییکه همواره \( \Large a\) از \( \Large c\) بزگتر است، خروج از مرکز بیضی همواره عددی بین 0 و 1 است. هر چه \( \Large e\) به 0 نزدیک تر باشد، بیضی بیشتر شبیه به دایره است. هر چه \( \Large e\) به 1 نزدیکتر باشد، بیضی کشیده تر است. به دو بیضی زیر نگاه کنید.
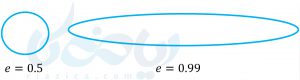

مثال 4: خروج از مرکز یک بیضی 0.8 است. اگر \( \Large F=(6, 12)\) و \( \Large F’=(6, 4)\) کانونهای آن باشند، اندازهی قطر کوچک را بیابید.
حل: فاصلهی کانونی که همان اندازهی \( \Large FF’\) میباشد، برابر است با:
\( \Large \sqrt{(6-6)^2+(12-4)^2}=8\)
پس مقدار \( \Large c\) که نصف فاصلهی کانونی است، برابر است با 4. از طرفی خروج از مرکز 0.8 است. پس:
\( \LARGE \frac{c}{a}=\frac{8}{10}\)
\( \LARGE c=4\Rightarrow a=5\)
\( \begin{aligned}\LARGE \Rightarrow b&\LARGE=\sqrt{a^2-c^2}\\&\LARGE=\sqrt{5^2-4^2}=3\end{aligned}\)
در نتیجه طول قطر کوچک برابر است با \( \Large 2b\) یعنی 6.
در ادامه حتما پست معادله دایره را مطالعه کنید.
زنگ آخر کلاس مقاطع مخروطی
در این درسنامه، ابتدا در مورد دوران و برش صحبت کردیم. با دوران یک خط حول خط متقاطع با آن، سطح مخروطی حاصل شد. با برشهای مختلف سطح مخروطی، مقاطع مخروطی مختلف به وجود آمد. به طور خاص در مورد بیضی به عنوان یکی از مقاطع مخروطی بیشتر صحبت کردیم. روابط مهم بیضی را به دست آوردیم و با حل چند مثال بسیار مهم، بر مطالب مسلط شدیم.
ما در ریاضیکا آمادهی هر کمکی برای موفقیت شما در ریاضی هستیم. هر سوالی در ارتباط با مبحث مقاطع مخروطی دارید، در دیدگاهها بنویسید. کارشناسان ما به سوال شما پاسخ خواهند داد.




