آموزش ریاضی پایه هشتم
با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
خرداد
اوووه! چقدر صفر داره این عدد! تازه باید 10 بار هم توی خودش ضربش کنم، بعد به یه عددی که 10 بار توی خودش ضرب شده تقسیمش کنم! کی میره این همه راه رو؟ اما اصلاً نگران نباشید! در این مطلب از مجموعه آموزش ریاضی پایه هشتم ، روش ضرب و تقسیم اعداد توان دار را یاد می‌گیریم. اون وقت برات مثل آب خوردن میشه… این درس رو از دست نده، چون با این مبحث در سال‌های بعد هم کار داریم، مثل توان‌های گویا.
یادآوری مفهوم توان
در ریاضی پایه هفتم یاد گرفتیم که توان ، خلاصه ضرب یک عدد در خودش است. مثلاً به جای آن که عدد 20 را 17 بار در خودش ضرب کنیم، آن را به صورت \(\Large 20^{17} \) مینویسیم.
در عدد \(\Large a^n \)، عدد \(\Large a \) را پایه و \(\Large n \) را توان می‌گویند.
نکته: \(\Large a^{-n} \) یعنی \( \Large \frac {1}{a^n} \) .
ضرب اعداد توان دار با پایه یا توان مساوی
در ضرب اعداد توان دار دو حالت برابر ممکن است رخ دهد:
- پایه‌ها برابر باشند.
- توانها برابر باشند.
۱. اگر پایه‌ها برابر باشند
در ضرب اعداد توان دار با پایه‌های برابر، یکی از پایه‌ها را نوشته و توانها را با هم جمع میکنیم.
\( \LARGE a^m × a^n = a^{m+n} \)
اگر \( \Large a^m × a^n \) را بصورت ضرب باز کنیم، دلیل این رابطه فهمیده میشود (دیده میشود که \( \LARGE a \) به تعداد \( \LARGE (m+n) \) بار در خودش ضرب شده است):
\( \LARGE 2^{10} × 2^4 \)
\( \LARGE =2^{(10+4)} = 2^{14} \)
۲. اگر توانها برابر باشند
در ضرب اعداد توان دار با توان های برابر، یکی از توان ها را نوشته و پایه‌ها را در هم ضرب میکنیم.
\( \LARGE a^m × b^m = (a×b)^m \)
اگر \( \Large a^m × b^m \) را بصورت ضرب باز کنیم، دلیل این رابطه فهمیده میشود (دیده میشود که \( \LARGE a×b \) به تعداد \( \LARGE m \) بار در خودش ضرب شده است):
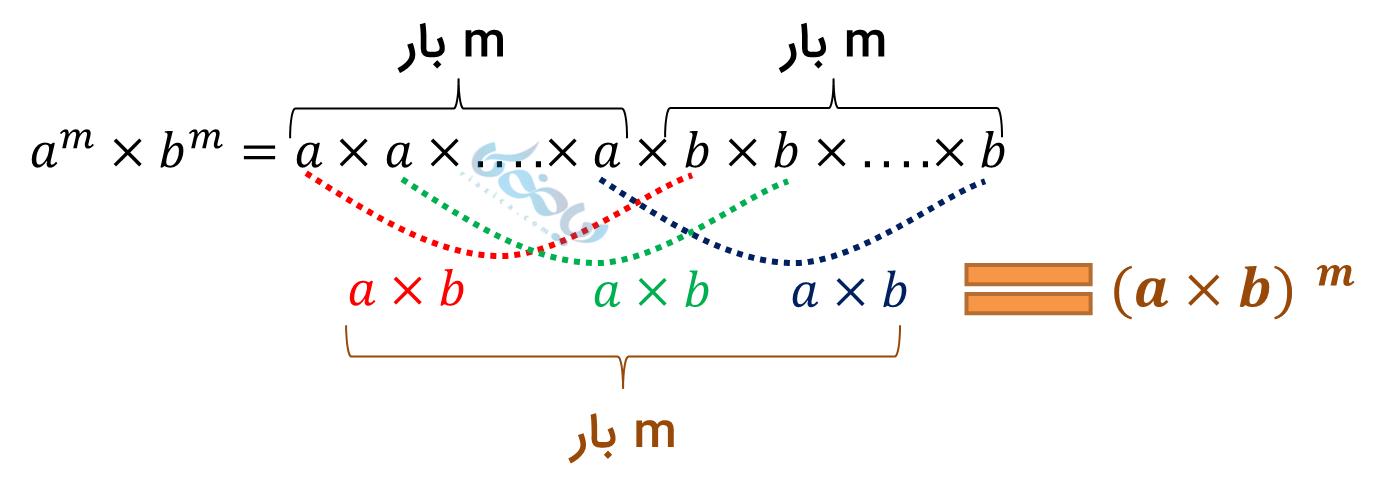
\( \LARGE 5/5^3 × 2^3 \)
\( \LARGE =(5/5 × 2)^3= 11^3 \)
به توان رساندن اعداد توان دار
برای محاسبه عدد \( \Large (x^c)^n \)، کافی است دو توان را در هم ضرب کنیم؛ یعنی:
\( \LARGE (x^c)^n=x^{c × n} \)
توجه داشته باشید که برای بدست آمدن این رابطه، در واقع از همان فرمول ضرب استفاده شده و عدد \( \Large (x^c)^n \) ، \( \Large n \) بار در خودش ضرب شده است.
تذکر: دقت کنید که وقتی توان عدد، به توان رسیده باشد، نباید از این رابطه استفاده کنیم. به عنوان نمونه عدد \( \Large 7^{5^2} \) برابر است با \( \Large 7^{25} \)؛ چون کل عبارت به توان نرسیده است.
مثال 1: حاصل عبارت \( \Large 4^6+4^6+4^6+4^6 \) را بدست آورید.
حل 1:
چهار عبارت مساوی با هم جمع شده است، این مفهوم ضرب در 4 است؛ بنابراین این عبارت برابر است با:
\( \LARGE 4 × 4^6 \)
\( \LARGE = 4^{(1+6)}=4^7 \)
تقسیم اعداد توان دار با پایه یا توان مساوی
برای تقسیم اعداد توان دار نیز دو حالت کلی وجود دارد:
- پایه‌ها برابر باشند.
- توانها برابر باشند.
۱. اگر پایه‌ها برابر باشند
در تقسیم اعداد توان دار با پایه‌های برابر، یکی از پایه‌ها را نوشته و توانها را از هم کم میکنیم.
\( \LARGE a^m \div a^n = a^{m-n} \)
(به شرطی که \(\Large a \ne 0 \))
\( \LARGE 256^9 \div 256^4 \)
\( \LARGE =256^{(9-4)} = 256^5 \)
۲. اگر توانها برابر باشند
در تقسیم اعداد توان دار با توان های برابر، یکی از توان ها را نوشته و پایه‌ها را بر هم تقسیم میکنیم.
\( \LARGE a^m \div b^m = (\frac {a}{b})^m \)
(به شرطی که \(\Large b \ne 0 \))
\( \LARGE 18^{22} \div 9^{22} \)
\( \LARGE =(\frac {18}{9})^{22}=2^{22} \)
جذر گرفتن از اعداد توان دار
برای محاسبه ریشه دوم (جذر) عدد \( \Large x^c \)، کافی است توان \( \Large c \) را بر 2 تقسیم کنیم، یعنی:
\( \LARGE \sqrt { x^c} =x^{\frac {c}{2}} \)
در واقع جذر گرفتن، مانند رساندن عدد به توان \( \Large \frac {1}{2} \) است. با آموزش ریشه‌گیری در سال‌های بعد بیشتر کار داریم.
مثال 2: حاصل ضرب و تقسیم‌های زیر را بدست آورید.
الف) \( \Large 2^5 × 6^5 \)
ب) \( \Large (- \frac {2}{5})^4 × (- \frac {2}{5})^6 \)
ج) \( \Large (0/022)^6 \div (0/022)^2 \)
د) \( \LARGE \frac {15^{1991}}{5^{1991}} \)
حل 2:
\( \Large 2^5 × 6^5 \) (الف
\( \Large =(2 × 6)^5= 12^5 \)
\( \Large (- \frac {2}{5})^4 × (- \frac {2}{5})^6 \) (ب
\( \Large =(- \frac {2}{5})^{4+6}=(- \frac {2}{5})^{10} \)
\( \Large (0/022)^6 \div (0/022)^2 \) (ج
\( \Large =(0/022)^{6-2}=(0/022)^4 \)
\( \LARGE \frac {15^{1991}}{5^{1991}} \) (د
\( \Large =(\frac {15}{5})^{1991}=3^{1991} \)
ضرب و تقسیم اعداد توان دار بدون پایه یا توان مساوی
اگر در ضرب و تقسیم اعداد توان دار، نه توان و نه پایه برابر نباشند، نمی‌توانیم از روش‌های قبلی استفاده کنیم. در این حالت باید هر عدد را به شمارنده‌های اول تجزیه کنیم (همان کاری که در فصل 2، درس اول کتاب انجام می‌دادیم) و سپس از روش ضرب و تقسیم اعداد با پایه یا توان مساوی استفاده کنیم.
مثال 3: حاصل عبارت \( \Large 28 × 2^{12} \) را بدست آورید.
حل 3:
برای محاسبه حاصل ضرب، باید ابتدا عدد 28 را به شمارنده‌های اول تجزیه کنیم:
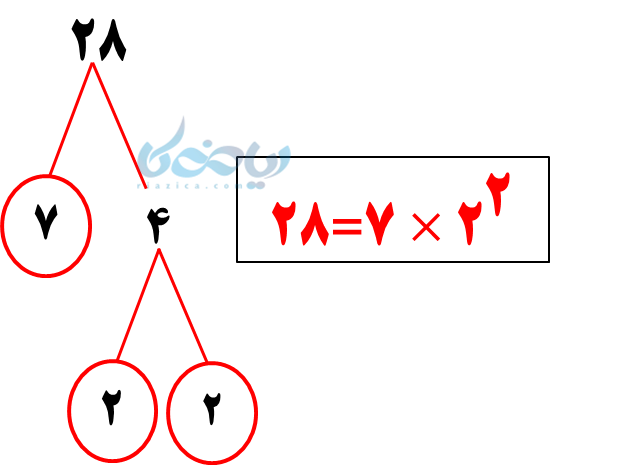
با جایگذاری تجزیه 28 به جای آن، ضرب تبدیل به ضرب اعداد توان دار میشود و خواهیم داشت:
\( \Large 7 × 2^2 × 2^{12} \)
\( \Large =7 × 2^{(2+12)} \)
\( \Large =7 × 2^{14} \)
مثال 4: عدد \( \Large 9^5 \) چند برابر بیست و هفت است؟
حل 4:
ابتدا 27 و \( \Large 9^5 \) را به عامل‌های اول تجزیه میکنیم و سپس عدد \( \Large 9^5 \) را بر 27 تقسیم میکنیم:
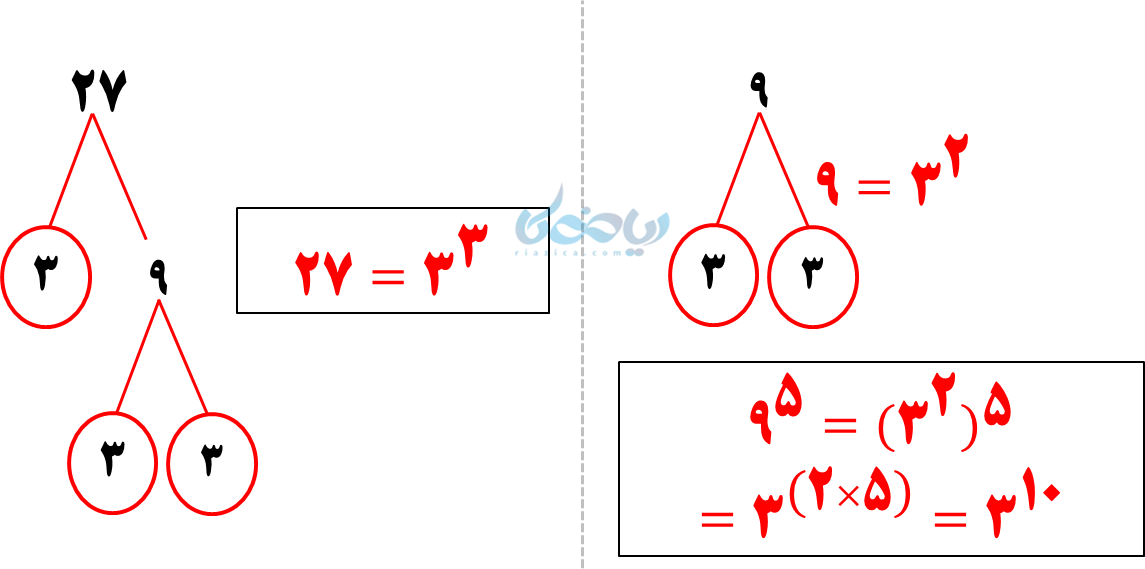
\( \LARGE \frac {3^{10}}{3^3} \)
\( \Large =3^{(10-3)}=3^{7} \)
ساده کردن کسرهای دارای اعداد توان دار
برای ساده کردن این کسرها، توان های مساوی و پایه‌های مساوی را مشخص کرده و جدا میکنیم. با این کار تبدیل به چند کسر شده و محاسبه آن ساده میشود. به نمونه زیر توجه کنید:
\( \LARGE \frac {3^4 × 2^9}{4^9 × 3^3} \)
\( \LARGE =\frac {3^4}{3^3} × \frac {2^9}{4^9} \)
\( \LARGE =3^{(4-3)} × (\frac {2}{4})^9 \)
\( \LARGE =3^1× (\frac {1}{2})^9 \)
\( \LARGE =\frac {3}{2^9} \)
مقایسهٔ اعداد توان دار
برای مقایسه باید پایه یا توان این اعداد را تا جای ممکن برابر کنیم.
به توان رساندن پرانتز
اگر در یک پرانتز چند عدد در هم ضرب یا بر هم تقسیم شده باشند و کل پرانتز به توان برسد، هر یک از اعداد به توان رسیده و به همان صورت ضرب و تقسیم میشود؛ به زبان ریاضی:
\( \LARGE (\frac {ab}{c})^n = \frac {a^n × b^n}{c^n} \)
نکته: علامت منفی به توان عدد زوج، مثبت و به توان عدد فرد، منفی میشود.
تذکر: به تفاوت \( \Large -4^2 \) و \( \Large (-4)^2 \) دقت کنید؛ اولی برابر با 16- و دومی برابر با 16+ می‌باشد.
مثال 5: اعداد \( \Large 4 \) ، \( \Large 2^{3^2} \)، \( \Large 2^3 \) ، \( \Large 8^4 \) و \( \Large (2^3)^2 \)را از بزرگ به کوچک مرتب نمایید.
حل 5:
برای مقایسه، پایه همه اعداد را برابر با 2 میکنیم (چون اگر اعداد 4 و 8 را تجزیه کنیم، پایه آنها 2 خواهد بود)؛ پس با نکاتی که از این درس آموخته ایم، این اعداد را با پایه 2 مینویسیم:
\( \Large 4 = 2^2 \) *
\( \Large 2^{3^2} = 2^9 \) *
\( \Large 2^3 \) *
\( \Large 8^4 = (2^3)^4 \) *
\( \Large =2^{3 × 4}=2^{12} \)
\( \Large (2^3)^2=2^{3 × 2}=2^6 \) *
خب! عددی بزرگتر است که توان بزرگتری دارد (یادتون نره؛ چون پایه‌ها برابرند). یعنی به ترتیب \( \Large 2^{12} \) ، \( \Large 2^9 \) ، \( \Large 2^6 \) ، \( \Large 2^3 \) و \( \Large 2^2 \) .
مثال کاربردی از اعداد توان دار در هندسه
مثال 6: حجم مکعبی به ضلع \( \Large 4x \) چند برابر حجم مکعبی به ضلع \( \Large x \) است؟
حل 6:
می‌دانیم حجم مکعب از سه بار ضرب کردن یک ضلع در خودش (یا همان به توان 3 رساندن یک ضلع) محاسبه میشود. پس حجم مکعبی به ضلع \( \Large 4x \) برابر است با:
\( \LARGE (4x)^3 = 4^3 × x^3 \)
\( \LARGE = 64x^3 \)
همچنین حجم مکعبی به ضلع \( \Large x \) برابر است با: \( \Large x^3 \) . حال برای این که بدانیم حجم اول چند برابر حجم دوم است، این دو را تقسیم میکنیم (پس حجم مکعب بزرگتر، 64 برابر مکعب کوچکتر است):
\( \LARGE \frac {64x^3}{x^3} = 64 \)
مثال 7: کسر زیر را تا جای ممکن ساده کنید:
\( \LARGE \frac {-2^2 × 81^{14}}{((-2) × 3)^{28}} \)
حل 7:
برای حل این سؤال مراحل زیر را طی میکنیم:
گفتیم برای ساده کردن کسر، باید تا جای ممکن پایه‌ها و توان ها را برابر کنیم
هم صورت و هم مخرج، عددی با پایه 2 دارد؛ پس می‌توانیم آن را نگه داریم. همچنین عدد \( \Large 81^{14} \) را می‌توان با تجزیه 81، بصورت \( \Large (9^2)^{14} \) نوشت که برابر با \( \Large 9^{28} \)، پس هم در صورت و هم در مخرج توان 28 داریم.
توجه: قبلاً گفتیم اعداد را به شمارنده‌های اول تجزیه میکنیم؛ اما در اینجا چون دیدیم مخرج دارای توان 28 بود، عدد 81 را بصورت \( \Large 9^2 \) نوشتیم.
پس تا اینجای کار کسر بدین صورت ساده شده است:
\( \LARGE = \frac {-2^2 × 9^{28}}{((-2) × 3)^{28}} \)
-
به توان رساندن کل پرانتز
کل مخرج کسر به توان 28 رسیده است، قبلاً گفتیم که هر عدد به توان رسیده و در هم ضرب میشود.
-
علامت منفی به توان یک عدد
توجه کنیم که در عبارت \( \Large -2^2 \) ، علامت منفی در پرانتز نیست، پس به توان نمی‌رسد. همچنین در مخرج کسر علامت منفی قبل از 2 چون به توان یک عدد زوج (28) می‌رسد، مثبت میشود.
\( \LARGE = \frac {-2^2 × 9^{28}}{2^{28} × 3^{28}} \)
-
نوشتن کسر بصورت ضرب دو کسر
این کسر را بصورت ضرب دو کسر با توان و پایه مساوی تبدیل میکنیم:
\( \LARGE = \frac {-2^2}{2^{28}} × \frac {9^{28}}{3^{28}} \)
-
انجام تقسیم‌ها
\( \Large = -2^{(2-28)} × (\frac {9}{3})^{28} \)
\( \Large = -2^{(-26)} × 3^{28} \)
با توجه به نکته ابتدای درس، می‌توانیم با انتقال عدد با توان منفی به مخرج، این کسر را بصورت زیر بنویسیم:
\( \LARGE = -\frac {3^{28} }{ 2^{26}} \)
قسمتی از فایل ویدیویی ضرب و تقسیم اعداد توان دار ➗✖️
برای خرید این محصول از دکمه خرید زیر این ویدیو استفاده کنید:
زنگ آخر کلاس ضرب و تقسیم اعداد توان دار
در این مطلب یاد گرفتیم که چگونه اعداد توان دار با توان یا پایه برابر را ضرب و تقسیم کنیم و اگر توان یا پایه برابر نداشتند، با تجزیه اعداد به شمارنده‌های اول توانستیم آنها را ضرب و تقسیم کنیم. در ادامه با حالت‌های خاصی مانند ساده کردن کسر، به توان رساندن پرانتز و مقایسه اعداد توان دار آشنا شده و با حل چندین مثال، کاملاً به این موضوع مسلط شدیم.
در صورتی که هر سؤالی از این مبحث داشتید، سوال خود را در پایین همین قسمت در دیدگاه‌ها برایمان بنویسید. کارشناسان ریاضیکا به سؤالات شما پاسخ خواهند داد.
ترتیبی که برای خواندن درسنامه‌های آموزش ریاضی هشتم به شما پیشنهاد می‌دهیم:
- اعداد صحیح 🧮📏 – نمایش روی محور مختصات
- تعریف اعداد گویا و … ! 🔢📝 همه چیز اینجاست!
- اعداد گویا – ✖️➗➖➕ چهار عمل اصلی
- عدد اول ریاضی هشتم 🥺🚶♂️ – کاملترین آموزشی که لازم داشتید.
- خط تقارن ریاضی هشتم ✂️ – چندضلعی تا خورده!
- خطوط موازی و مورب 📏📐 ؛ رانندگی خطها در چهارراه زاویه!
- چهار ضلعی ها ✏️📋 – آشنایی با یک خانواده جذاب!
- زاویه های داخلی ❌⚔️ – نیروهای جوان کشور چندضلعی‌ها!
- زاویه های خارجی 🕙♦️🕑 – نگهبان قلعه چندضلعی‌ها!
- ساده کردن عبارت های جبری 😎🧮 ؛ مختصر و مفید با صدای بلند!
- فاکتورگیری ریاضی هشتم 🧮📚 – هنرمندانه از عبارتهای جبری استفاده کن!
- حل معادله درجه اول 🥇💎 – سرآغاز یک بحث شیرین ریاضی!
- بردار و مختصات ریاضی هشتم 📍📌🗺 – جهتدار و کامل!
- بردارهای واحد مختصات 📉📈 – قدم قدم بشمار!
- رابطه فیثاغورس ریاضی هشتم 📐📕 – وزیر بازی مثلثات!
- شکل های هم نهشت آموزش ریاضی هشتم 🔍🔎 – کپی برابر اصل!
- مثلث های هم نهشت 📐🖍️ گل سرسبد شکل‌های هم‌نهشت!
- با ضرب و تقسیم اعداد توان دار ➗✖️، توانت رو بالا ببر! آموزش ریاضی هشتم
- جذر تقریبی هشتم 😍 – گام به گام یاد بگیر
- نمایش اعداد رادیکالی روی محور اعداد ریاضی هشتم ✏️📐📏 یک نمایش بی نقص
- خواص ضرب و تقسیم رادیکال ها ریاضی هشتم ✖️➗ – یک‌ضرب یاد بگیر!
- همه چیز درباره جدول فراوانی 🗺️ ریاضی هشتم – دادههای آماری
- آموزش احتمال هشتم 🎲👍 : احتمال رخ دادن پیشامد – احتمالاً نه! حتماً یاد میگیرید
- خط و دایره : از سیر 🧄 تا پیاز 🧅
- زاویه های دایره : زاویه محاطی و زاویه مرکزی ⭕️📐 – مبحثی کاربردی در هندسه!
- جمع و تفریق اعداد صحیح ➕➖ – صحیح و سالم به مقصد برسید!
واقعا ممنونم ، نجاتم دادید
سلام ممنون از انرژیتون. خوشحالیم که موثر و نجات بخش بوده.
داداش 3 بتوان 10 درسته ن ب توان 20.
با سلام به شما دوست خوبم
اول از همه ممنون از مطالعه درسنامه‌های سایت
و بعد از اون تشکر بابت دقت نظرتون. اصلاح شد
باز هم منتظر نظرات شما دوستان عزیز هستیم.
خدا خیرت بده
سلام عرض ادب
ممنون از انرژی پرمهرتون
موفق باشید
باسلام ببخشیداگردرضرب یاتقسیم یک عددتواندارکه هم توانهابرابر هم پایه هابرابرباشندپاسخ چیست؟مچکرم
سلام و عرض ادب
شما در این حالت می توانید یا از روش پایه های برابر بروید یا از روش توان های برابر.
هر دو روش را باهم بکار نبرید.
موفق باشید.
جواب این عبارت را به صورت اعداد توان دار بنویسید
۵ به توان ۴ × ۲۷ به توان ۳
_______________________بر روی
۲۵ به توان ۶ × ۳
سلام عرض ادب
جواب:
۳ به توان ۸ ضربدر ۵ به توان ۱۰-
موفق باشید.
سلام.ممنون از سایت خوب و مطالب مفیدتون.
ولی پاسخ سوال قبل میشه کسر 3/5 به توان 8
با سلام واحترام
میشه بگید دقیقا کدوم رو میفرمایید
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام مطالب شما عالی بود . اما نگفتید که اگر هم پایه و هم توان برابر باشند باید چیکار کنیم . مثلا: ۱۵ به توان ۲ ضربدر ۱۵ به توان ۲ .
سلام وعرض ادب
خوشحالیم که مفید بوده یا یکی از پایه ها را بنویسید توانها را جمع کنید یا یکی از توانها را بنویسید پایه ها را ضرب کنید
با سلام و خسته نباشید
اگه میشه این سوال رو برام حل کنید
این عبارت را به صورت اعداد توان دار جواب دهید
۵ به توان ۴ × ۲۷ به توان ۳
________________________ بر روی
۲۵ به توان ۶ × ۳
سلام عرض ادب
جواب:
۳ به توان ۸ ضربدر ۵ به توان ۱۰-
موفق باشید.
سلام سوالتون رو کامل بنویسید. ممنون
تقسیمات توان هم بگید خواهشا !!
سلام و عرض ادب
در همین پست به طور کامل این موضوع بررسی شده است.
موفق باشید.
سلام اگه نه توان و پایه ها برابر باشه باید چیکار کنیم؟
با عرض سلام
در این صورت فقط مقدار عبارت رو میشه به دست آورد
مثلاً ۸به توان ۴….ضربدر ۳به توان ۱۳……حاصل یه عبارت تواندار بود…و الان ما به این رسیدیم یعنی دیگ نمخاد کاری کنیم؟و باید همینطور بنویسیم؟؟
با سلام
نه چون حتی اگر ۸به توان ۴ رو بنویسیم ۲ به توان ۱۲ باز نه پایه برابر هست نه توان ونمیشه به صورت یک عدد تواندار نوشت
یج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام حاصل
۴ به توان ۹ ضربدر ۲ به توان ۹ تقسیم بره ۸ به توان ۶ میشه چند؟
سلام و عرض ادب
جواب برابر با ۵۱۲ می شود.
موفق باشید.
سلام اگر در مقایسه اعداد توان دار نه پایه و نه توان برابر نبود باید چیکار کنیم
مثلا : دو به توان سیصد بزرگتر است یا سه به توان دویست
با سلام وعرض ادب
دو به توان ۳۰۰ رو میتونی بنویسی 100^(2^3),۲به توان ۲۰۰ رو میتونی بنویسی 100^(3^2) حالا توانها هر دو ۱۰۰ است کدام بزرگتر است ؟۳به توان ۲۰۰ بزرگتر است
سلام
با سلام وعرض ادب
بفرمایید
سلام .ممنون به خاطر درسنامه
ببخشید اگر بگن …… برابر یک عدد توان دار را به صورت توان دار بنویسید چجوری باید حل کنیم ؟
مثلا بگیم 16 برابر 8به توان 5 را به صورت عدد توان دار بنویسید
با سلام وروز به خیر
کافیه ۱۶ رو بنویسید ۲به توان ۴ و۸رو بنویسیم ۲به توان ۳ یه توان ۵ داشت پس میشه ۲به توان۱۵ حالا پایه ها برابرند توانها جمع میشه ۲به توان ۱۹
پیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
ممنون از آموزشهای خوب و بینظرتان در ضمن در مطلب بالا(در ساده کردن کسرهای دارای اعداد توان دار) که یک مثال زده اید . حل آن مثال اشتباه نوشته شده است
باسلام وعرض احترام
ممنون از توجه شما اصلاح شد
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
با سلام وعرض احترام
ممنون از توجه ولطف شما اصلاح شد
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام
میشه بگین اگه توان ها روی هم باشند اونارو چطوری حساب میکنیم
ممنون ❤
با سلام واحترام
در مثال ۵ توضیح دادیم
برای اطلاع از جشنواره ها ومطالب بیشترپیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام برای به توان رسوندن دو عدد بدون استفاده از توان و ضرب باید چه کار کنیم؟؟؟ مثلا 2 و 4؛
4^2 به این شکل نه یا 2*2*2*2 به این شکل.
راه حل دیگه ای داره؟؟؟
لطفا بگید خیلی گیرم اگه میشه تو ایمیلم بفرستید یا تو تلگرام به آیدی PHobos_800723@
ضمن عرض سلام
برای به توان رساندن هیچ راه حل میانبری وجود ندارد.
برای اطلاع از جشنواره ها ومطالب بیشتر پیج ما رو در اینستا به آدرس زیر دنبال کنید
https://www.instagram.com/riazica/
سلام و عرض خسته نباشید.
میخواستم بدونم وقتی در ضرب عبارت های توان دار، نه توان و نه پایه برابر باشند جواب چیست؟
ممنون میشم پاسخ منو بدین
با سلام وعرض ادب
گاهی پایه ها عدد مرکب هست ووقتی تجزیه میشه پایه ها مساوی میشه در غیر این صورت فقط میشه مقدار عبارت رو به دست اورد ونمیشه به صورت یک عدد تواندار نوشت
سلام ممنون بخاطر سایت خوبتون
میخواستم بدونم وقتی در ضرب عبارت های توان دار، نه توان و نه پایه برابر باشند جواب چیست؟
ممنون میشم پاسخ منو بدین
با سلام وعرض ادب
گاهی پایه ها عدد مرکب هست ووقتی تجزیه میشه پایه ها مساوی میشه در غیر این صورت فقط میشه مقدار عبارت رو به دست اورد ونمیشه به صورت یک عدد تواندار نوشت
سلام ببخشید اگر 5x=20 باشد حاصل 5x+12 چند است ؟
ضمن عرض سلام
این سوال جزو سوالاتی است که ما معتقدیم دانش آموزانی که از محتوای ما استفاده می‌کنند باید در لحظه به آن پاسخ دهند. برای یادگیری کامل این مبحث به لینک زیر مراجعه بفرمایید:
https://riazica.com/solve-the-first-degree-equation/
اول طبق معادلهx رو بدست میاریم که برابر هست با ۴ و بعد از این شما راحت میتونید عبارت رو بدست بیاری که میشه ۳۲
با سلام واحترام ممنون از پاسخگویی شما ولی ما این همه محتوا روی سایت به صورت رایگان قرار دادیم تا خود دوستان به جواب سوالات برسند نه ازما انتظار داشته باشند حل المسایل آنها باشیم
سلام
حاصل21^2×14^3چقدر است؟
با سلام وعرض ادب
دوست عزیز جواب میشود هفتاد دو به توان ۷
سلام
۹بتوان aمیشه۲۰۰۰
۹بتوانbمیشه ۶۰۰۰
9بتوان(2+a+b)چند میشه؟
با سلام
میشود ۲۰۰۰ضربدر ۶۰۰ضربدر ۸۱
ببخشید جواب 4 ، بیستم به توان 7 ضربدر دو دهم ضربدر 1 به توان 15 میشه چند؟
با سلام وعرض ادب
هر دو پایه مساوی یک پنجم میشود پس یکی از پایه ها رو نوشته توانها رو جمع میکنیم
سلام ببخشید ۱۰ به توان ۱۴_ تقسیم بر ۰.۲ چند میشه؟
با سلام واحترام
به این صورت که شما نوشتید میشه 5ضربدر 10 به توان 14
سلام خیلی ممنون بابت گردآوری و خلاصه عالیتون فقط اولای درسنامه یه قسمت هست که چهارتا چهار به توان شیش با هم جمع شدن و باید مفهوم توان روی توان رو برسونن ولی جواب چهار به توان هفت شده در صورتی که چهار به توان۲۴ حاصل میشه
با سلام وعرض ادب
در این مثال بین آنها جمع هست پس نمیشه توانها رو جمع کرد وای چون چهارتا چها به توان شش بوده مینویسیم چهار ضربدر چهار به توان شش
سلام شنبه امتحان ریاضی حصوری دارم پایه ی نهمم دلم گرفته دعا کنید تا خوب بیارم تا بتونم تجربی بردارم
هر کس فقط ی صلوات بفرسته کافیه توروخدا 🥺🥺
با عرض سلام وادب
شما تلاش کن حتما خدا کمک میکنه
خیلی ممنون واقعا💜معلم امسال ما خیلی خیلی تنبل بود و هیچی نمیفهمیدیم هی فیلمای معلمای دیگ رو میفرستاد😒
من کلاس هشتم هستم و مطالبتون واقعا خیلیییییییی ب دردم خورد فردا امتحان ریاضی دارم
پیج اینستاتونم با گوشی مامانم فالو کردم و نشستم پستاتونو دیدم خیلی ممنون واقعا ایشالا هرچی از خدا میخواین بهتون بده💜🎀
با سلام وعرض ادب
ممنون از توجه شما خوشحالیم که مطالب سایت برا شما مفید واقع شده
سلام خدمت شما وقتی پایه ها و توان ها باهم برابر نبود ولی از ما خواستند که به صورت عددی توان دار بنویسیم باید چکار کنیم
مثال ۲به توان ۳ ضبدر ۶بتوان ۵
با سلام وعرض ادب
فقط میشه مقداربدست آورد
سلام وقتتون بخیر باشه❤
مطالبتون خیلی خوب بود دستتو ن درد نکنه❤واسه ی امتحان ریاضیم اینا رو بلد نبودم ولی مطالب شما کامل و به صورت واضح هستش واسه همین خیلی خوب فهمیدم❤
مرسی ازتون❤
با سلام واحترام
خدا رو شکر مطالب سایت برای شما مفید واقع شده
سلام خسته نباشید💕
من میخواستم درسا رو قبل شروع سال تحصیلی جدید یه دور بخونم ولی راستش تو این مباحث خیلی به مشکل بر میخوردم
سایتتونو دوستم بهم معرفی کرد خیلی ممنون که به فکر دانش آموزا هستید💕
انشالله از خدا هرچی که میخواین بهتون بده💕
با سلام وعرض ادب اولا آفرین به شما که از الان به فکر سال تحصیلی سال آینده هستید وممنون از نظر شما نسبت به سایت ما اگه سال نهم میرید و در امتحان تیزهوشان ونمونه دولتی میخواهید شرکت کنید گوش به زنگ باشید که برنامه ویژه ای براتون داریم
باسلام ممنون از ارائه مطالب جامع و مفید شما
ی سئوالی داشتم
در مسائلی که نه توان برابره نه پایه و نمیشه هم با تجزیه یکی از این دوتا رو برابر کرد و فقط میشه مقدار رو بدست آورد قطعا زمانبر هست اگه مقدار توان زیاد باشه و احتمال خطا زیاده بدلیل ضرب های زیاد
شما راه حلی دارید که اینطور مسائل رو در کنکور که از ماشین حساب هم نمیشه استفاده کرد چطور بدون خطا و با سرعت بالا حل کرد؟
با سلام و عرض ادب
در دوره محاسبات سریع که در روی سایت موجود هست ضربها و وتوان رساندم سریع رو بیان‌کردیم میتونید تهیه و استفاده کنید